 Périphériques technologiques
Périphériques technologiques
 IA
IA
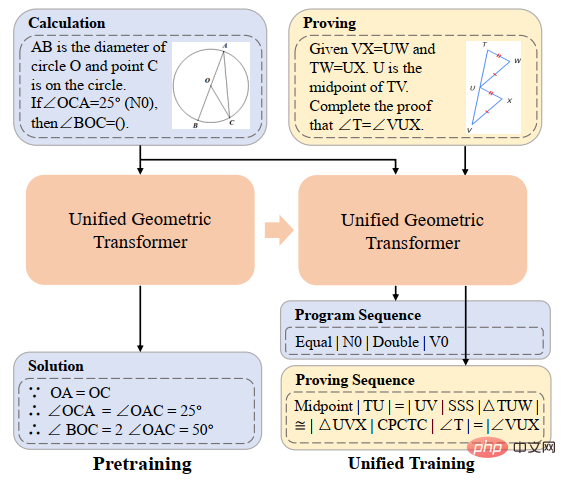
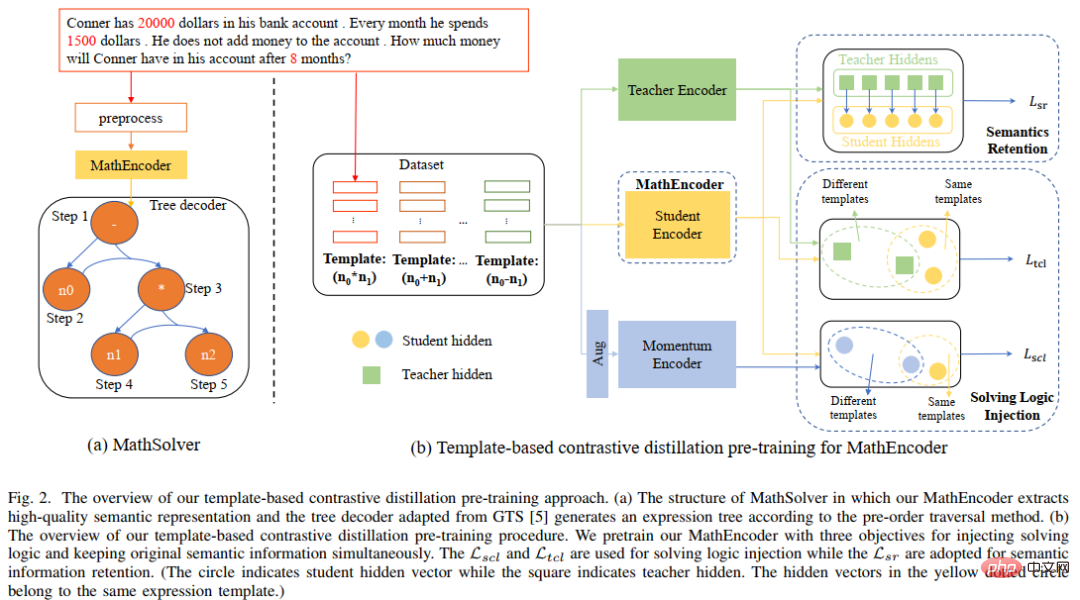
 Équipe HCP Lab de l'Université Sun Yat-sen : De nouvelles avancées dans la résolution de problèmes d'IA et les réseaux de neurones ouvrent la porte au raisonnement mathématique
Équipe HCP Lab de l'Université Sun Yat-sen : De nouvelles avancées dans la résolution de problèmes d'IA et les réseaux de neurones ouvrent la porte au raisonnement mathématique
Équipe HCP Lab de l'Université Sun Yat-sen : De nouvelles avancées dans la résolution de problèmes d'IA et les réseaux de neurones ouvrent la porte au raisonnement mathématique
Les êtres humains ont besoin de maîtriser de nombreux points de connaissances pour résoudre un grand nombre de problèmes mathématiques à différentes étapes de leur processus de croissance. Cependant, comprendre les points de connaissance ne signifie pas que vous les comprenez vraiment. Ce n'est qu'en étant capable de résoudre les problèmes que vous pourrez refléter la sagesse humaine. Ces dernières années, les réseaux de neurones ont connu un grand succès dans les domaines de la vision par ordinateur, de la correspondance de modèles, du traitement du langage naturel, de l'apprentissage par renforcement, etc. Cependant, la capacité de raisonnement par combinaison discrète des modèles de réseaux de neurones est bien inférieure à celle des humains. Alors, les réseaux de neurones peuvent-ils comprendre les problèmes mathématiques et les résoudre ? Si oui, quelle est la capacité des réseaux de neurones à résoudre des problèmes ?
En termes de forme de données, un problème mathématique peut être considéré comme une séquence, et sa solution (étapes ou expressions de résolution de problème) est souvent présentée sous la forme d'une séquence. La résolution de problèmes mathématiques peut alors être considérée comme un problème de traduction du langage naturel vers le langage mathématique. Le modèle de réseau neuronal peut résoudre formellement des problèmes mathématiques. Il ressort de divers travaux de recherche antérieurs que les réseaux de neurones peuvent atteindre de très bonnes performances sur les problèmes de traduction et ont surpassé les performances humaines sur plusieurs ensembles de données. Cependant, elle est très différente de la traduction automatique. En plus de la capacité à comprendre la sémantique de la question, la résolution de problèmes mathématiques nécessite souvent que le modèle ait la capacité de raisonner sur des combinaisons discrètes d'objets et d'entités algébriques généralisées.
Afin d'explorer la capacité des modèles profonds à résoudre des problèmes mathématiques, le laboratoire d'intégration de l'intelligence humaine-machine de l'université Sun Yat-sen a mené une série d'expériences basées sur des recherches antérieures, en utilisant des problèmes d'application mathématiques et des problèmes de calcul géométrique en primaire. et les écoles secondaires comme point de départ. La recherche améliore la compréhension sémantique, le raisonnement cognitif et les capacités de résolution de problèmes mathématiques des modèles profonds. Cet article présentera brièvement une série de recherches dans le domaine de la résolution de problèmes mathématiques menées par le Laboratoire d'intégration intelligente homme-machine-objet de l'Université Sun Yat-sen.
Article 1 : Solveur universel structuré en arbre sémantiquement aligné pour les problèmes de mots mathématiques

La conférence 2020 sur les méthodes empiriques dans le traitement du langage naturel
Adresse papier : https://aclanthology.org/2020.emnlp-main.309.pdf
Un solveur pratique de problèmes de mots mathématiques devrait être capable de résoudre divers types de problèmes de mots mathématiques, tels que les équations linéaires à une variable, les équations linéaires de deux groupes de variables, équations quadratiques, etc. Cependant, la plupart des travaux de résolution de problèmes d'application mathématique ne sont conçus que pour quatre opérations arithmétiques, et ce type de conception est souvent difficile à étendre à davantage de types de questions. Il est impossible d'utiliser un solveur de problèmes d'application mathématique unifié pour résoudre différents types d'expressions à la fois. en même temps. De plus, la plupart des solutions actuelles de problèmes de mots mathématiques manquent de contraintes sémantiques entre le texte du problème et l’expression de la solution.
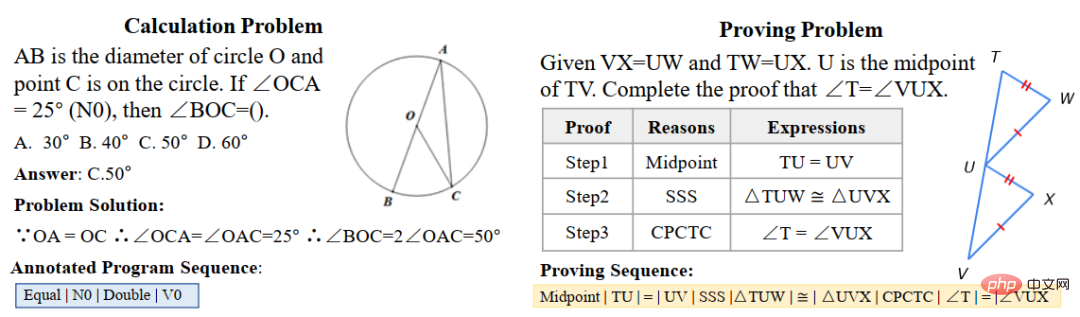
En réponse aux problèmes ci-dessus, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'université Sun Yat-sen a proposé un schéma de représentation d'arbre d'expression unifié en introduisant des opérateurs supplémentaires pour connecter plusieurs expressions, une équation linéaire d'une variable et un système. des équations linéaires à deux variables sont , les équations quadratiques et d'autres types d'expressions sont exprimées de manière unifiée, ce qui peut simplifier la conception du solveur et résoudre divers types de problèmes d'application, comme le montre la figure 1.
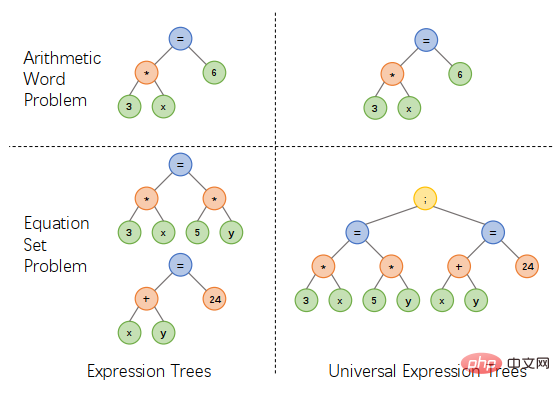
Figure 1 Conception d'un schéma de représentation d'arbre d'expression unifié
Basé sur le schéma de représentation d'arbre d'expression unifié, nous proposons en outre un solveur universel de structure arborescente sémantiquement aligné (SAU-Solver), comme indiqué dans la figure 2. Notre solveur universel structuré en arborescence se compose de deux parties, un encodeur de problèmes basé sur un GRU à deux couches et un décodeur arborescent basé sur une représentation arborescente d'expression unifiée. Et pendant le processus de formation, nous avons introduit la régularisation de l'alignement sémantique. En limitant la cohérence du sous-arbre d'expression et du contexte de la question, notre solveur général peut considérer plus complètement la relation sémantique entre le problème et l'expression et explorer divers types de problèmes mathématiques. connaissances, améliorant ainsi les capacités de génération d’expressions du solveur.
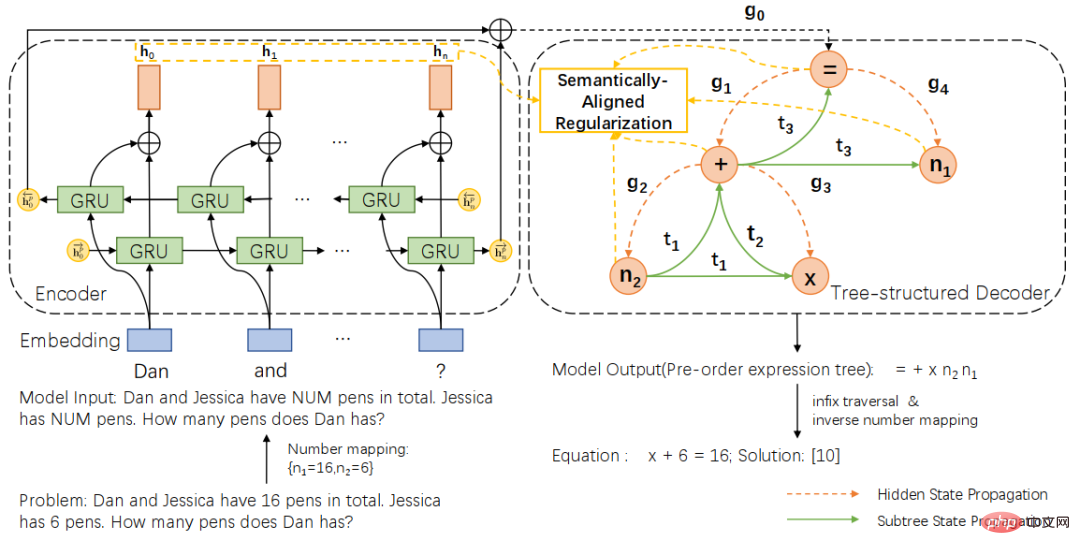
Figure 2 Solveur de structure arborescente d'alignement sémantique
De plus, afin de mieux mesurer la polyvalence et les capacités de résolution du solveur, nous avons également construit un ensemble de données multi-questions de taille moyenne HMWP pour les problèmes avec un seul type de questions dans l'ensemble de données d'annotation actuel. comprend Résoudre des milliers de questions textuelles mathématiques de divers types d'expression telles que les équations linéaires à une variable, les systèmes d'équations linéaires à deux variables, les équations quadratiques à une variable, etc. Nos expériences montrent que les ensembles de données comportant plusieurs types de questions sont plus difficiles pour les solveurs que les ensembles de données comportant un seul type. Ils peuvent également mieux mesurer la capacité du solveur à résoudre des problèmes et promouvoir la recherche dans la communauté des solveurs.
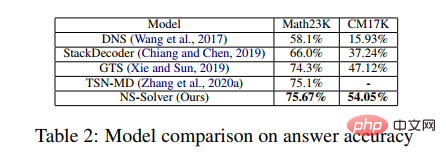
Dans l'expérience, l'article a comparé le SAU-Solver proposé avec les méthodes existantes dans HMWP, Math23K, ALG514 et Dolphin18K-Manual. Les résultats expérimentaux sont présentés dans la figure ci-dessous, qui prouve la polyvalence et la meilleure capacité de résolution de problèmes mathématiques de notre méthode.
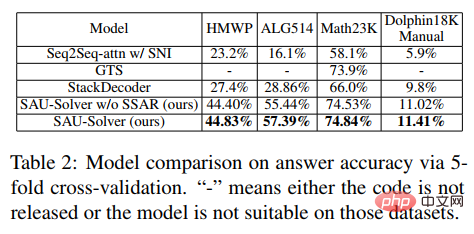
Pour plus de détails sur la recherche, veuillez vous référer à l'article original.
Papier 2: Solveur symbolique neural pour les problèmes de mots mathématiques avec les tâches auxiliaires

La 59e réunion annuelle de l'Association for Computational Linguistics et la 11e Conférence conjointe internationale sur le traitement du langage naturel
Adresse papier : https://arxiv.org/abs/2107.01431
Les résolveurs actuels de problèmes de mots en mathématiques élémentaires ne prennent pas en compte diverses contraintes de symboles mathématiques, mais utilisent simplement des encodeurs - Problèmes avec le cadre du décodeur, conduisant à des prédictions déraisonnables. L'introduction de contraintes symboliques et de raisonnements symboliques est très critique pour résoudre automatiquement les problèmes d'application mathématique.
Par conséquent, l'équipe du Laboratoire d'intégration de l'intelligence humaine-machine de l'Université Sun Yat-sen a introduit le paradigme informatique neuro-symbolique et a proposé un nouveau solveur neuro-symbolique (NS-Solver) pour effectuer une injection explicite de connaissances sous forme de tâches auxiliaires. , Implémentez ainsi des contraintes symboliques à différents niveaux. Son architecture technique est présentée à la figure 3. NS-Solver est construit sur l'épine dorsale du réseau par trois composants : 1) Lecteur de problèmes, qui effectue une compréhension sémantique et une représentation efficaces des problèmes mathématiques via un réseau GRU bidirectionnel à deux couches 2) Programmeur, qui est responsable du raisonnement symbolique ; sur la sémantique du problème et les résultats de prédiction de bon sens, générer l'expression de la solution. 3) Exécuteur, utilisez la bibliothèque sympy pour résoudre des expressions et obtenir la réponse finale.
Concernant les contraintes de symboles, nous proposons une variété de tâches auxiliaires pour utiliser des signaux d'entraînement supplémentaires et utiliser les résultats de prédiction de bon sens pour contraindre explicitement la table de symboles et réduire l'espace de recherche de résolution de problèmes : 1) Tâche de prédiction de chiffres auto-supervisée : via Prédire la position et le nombre de nombres dans la question pour mieux comprendre la sémantique de la question ; 2) Tâche de prédiction de quantificateur de bon sens : injecter des connaissances de bon sens et utiliser les résultats de la prédiction pour contraindre la table de symboles, réduisant ainsi l'espace de recherche ; check : Vérifier la résolution du problème au niveau sémantique. La cohérence entre la sortie du solveur et l'expression cible ; 4) Tâche à double utilisation : Renforcer la compréhension sémantique du problème du solveur à travers les contraintes bidirectionnelles du problème à l'expression et à l'expression. au problème.
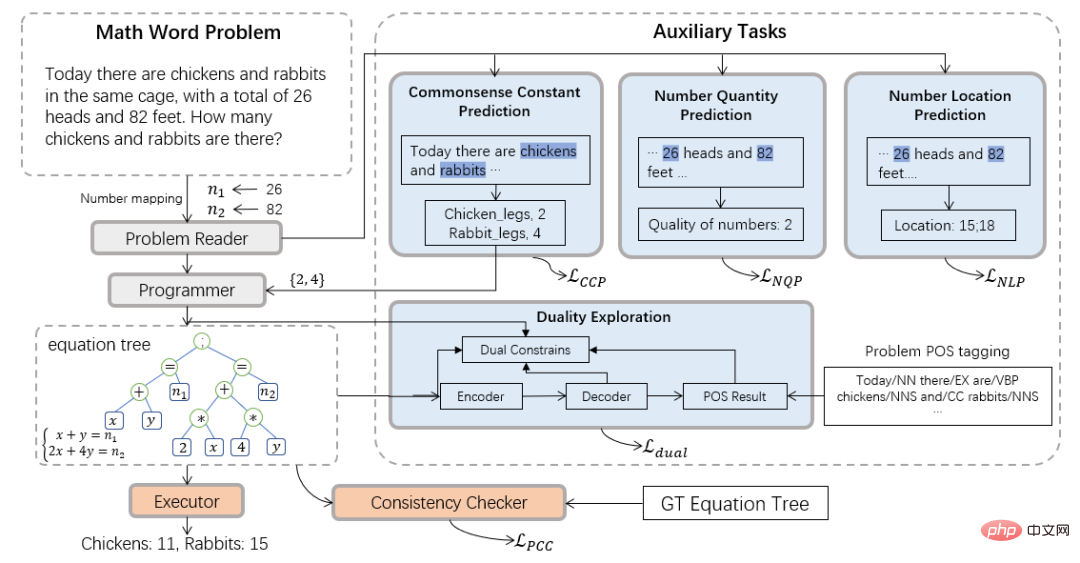
Figure 3 Solveur neuro-symbolique (NS-Solver)
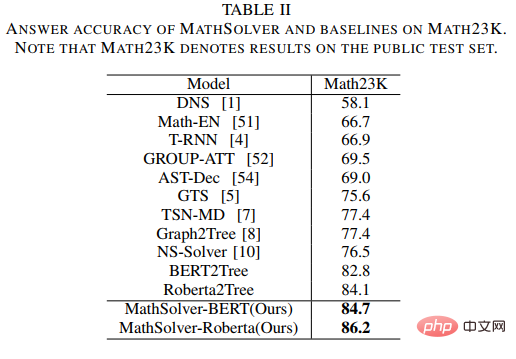
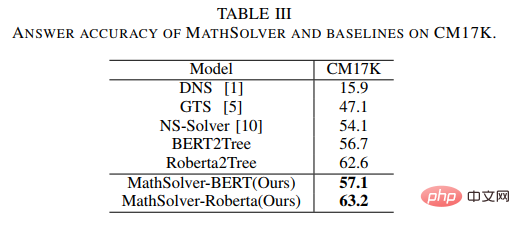
De plus, afin de mieux vérifier les performances du solveur, nous avons également construit un multi-problèmes à plus grande échelle tapez l'ensemble de données sur les problèmes d'application des mathématiques CM17K, afin de mieux promouvoir la recherche dans la communauté de résolution de problèmes mathématiques. CM17K contient 6 215 problèmes arithmétiques à quatre variables, 5 193 équations linéaires à une variable, 3 129 équations non linéaires à une variable et 2 498 problèmes d'équations. Les statistiques du CM17K et du Math23K sont présentées dans le tableau ci-dessous. Il ressort des statistiques que le CM17K a des informations sur les questions plus longues, des expressions de solutions plus longues et implique plus de bon sens que Math23K, ce qui signifie que le CM17K caractérise mieux les performances du résolveur de problèmes en termes de difficulté de résolution.
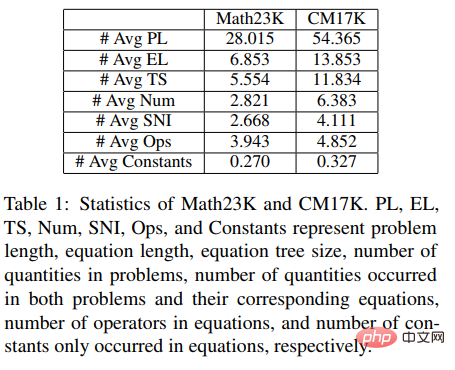
Dans l'expérience, l'article a comparé le NS-Solver proposé avec les méthodes existantes sur Math23K et CM17K, et a mené des expériences d'ablation, qui ont prouvé la bonne capacité de résolution de problèmes et la polyvalence du NS-Solver. Les résultats expérimentaux sont présentés dans les deux tableaux suivants.
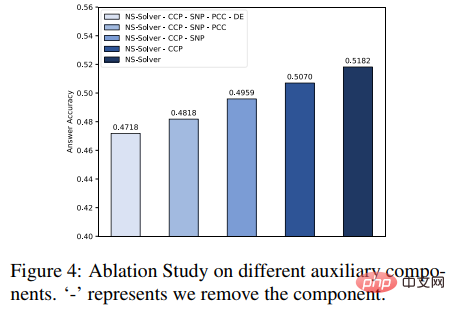
De plus, nous avons également mené des expériences d'ablation sur des tâches auxiliaires, comme le montre la figure ci-dessous. Les résultats expérimentaux prouvent que chaque tâche auxiliaire peut améliorer la capacité de résolution de problèmes de NS-Solver.
Pour plus de détails sur la recherche, veuillez vous référer à l'article original.
Article 3 : GeoQA – Une question géométrique répondant à une référence pour un raisonnement numérique multimodal

Résultats de l'Association for Computational Linguistics : ACL-IJCNLP 2021
Adresse papier : https://arxiv.org/pdf/2105.14517.pdf
La résolution automatique de problèmes mathématiques a attiré de plus en plus d'attention récemment. Résolution automatique de problèmes mathématiques La plupart des travaux se concentrent sur la résolution automatique de problèmes mathématiques. Cependant, peu de travaux se concentrent sur les problèmes de géométrie. Par rapport aux questions d'application des mathématiques, les questions de géométrie nécessitent la compréhension simultanée des descriptions de texte, des graphiques et des diagrammes, car dans les questions de géométrie, le texte de la question, les graphiques et les diagrammes se complètent généralement et sont indispensables. Les méthodes existantes pour résoudre automatiquement les problèmes de géométrie dépendent fortement des règles et sont évaluées uniquement sur de petits ensembles de données.

Figure 4 Exemples de questions de géométrie
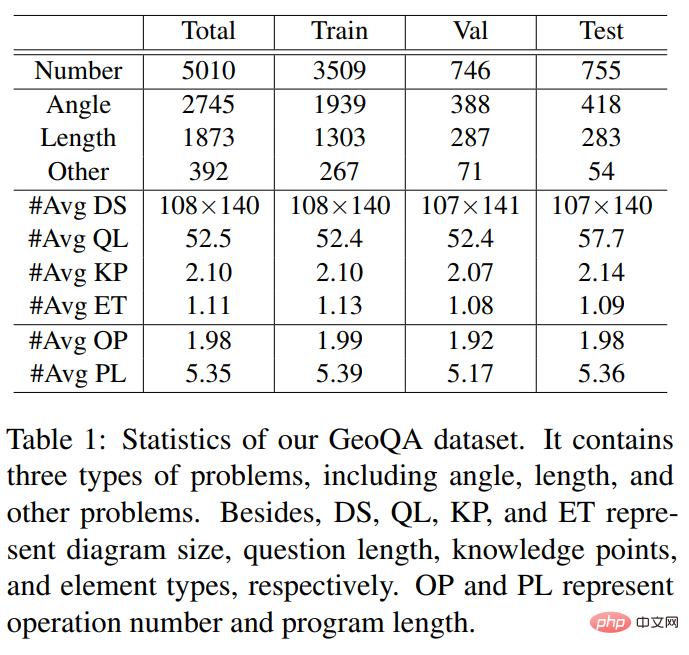
Afin de promouvoir la recherche sur la solution automatique des questions de géométrie, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'Université Sun Yat-sen a construit une question de géométrie consistant sur 5010 questions à choix multiples La question répondant à l'ensemble de données GeoQA. Comme le montre la figure 4, chaque échantillon de l'ensemble de données GeoQA comporte une description de question, une image géométrique, des options de question, des réponses, des types de questions, des points de connaissance, une analyse de solution et des procédures formelles marquées par des étapes de résolution de problèmes. En termes de taille du problème, cet ensemble de données est 25 fois plus grand que l'ensemble de données GeoS couramment utilisé dans les travaux précédents. Les informations statistiques pertinentes de l'ensemble de données GeoQA sont présentées dans le tableau ci-dessous.
Les opérateurs formels du programme et les constantes impliquées utilisées par l'ensemble de données GeoQA sont présentés dans le tableau ci-dessous.

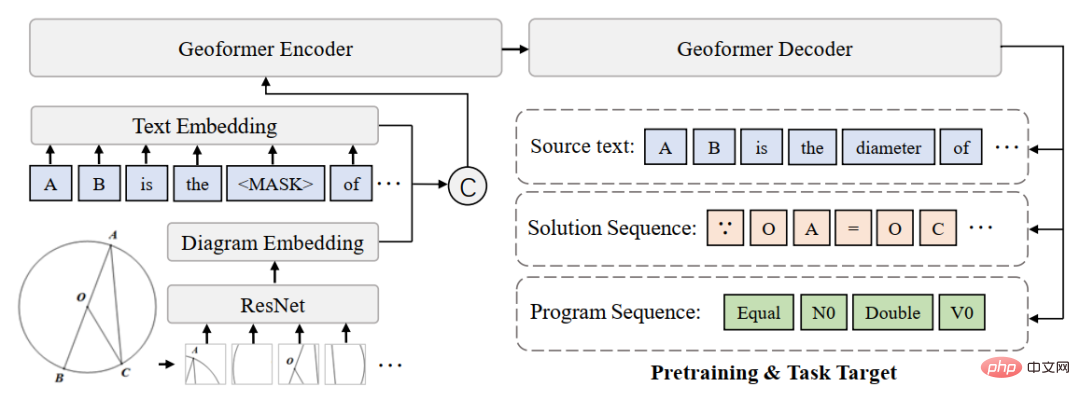
Afin de mieux promouvoir la recherche de solutions de problèmes de géométrie, en plus de construire des modèles de base basés sur l'ensemble de données GeoQA, nous avons également proposé le solutionneur de problèmes de neurogéométrie NGS pour comprendre les informations sémantiques multimodales et générer programmes formels interprétables. La conception globale du solutionneur de problèmes neurogéométriques NGS est présentée à la figure 5.
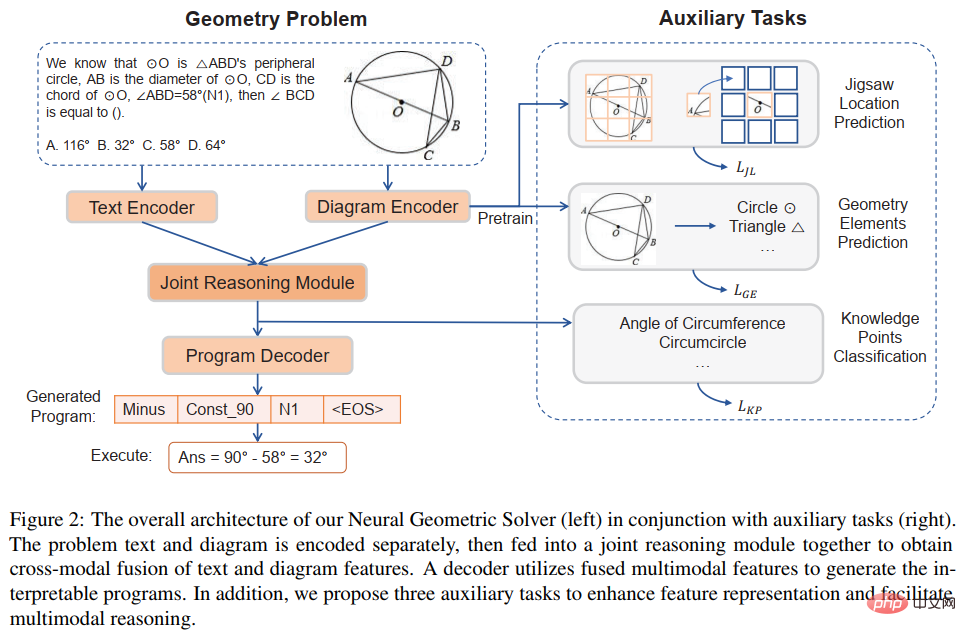
Figure 5 Diagramme schématique du solutionneur de problèmes de neurogéométrie (NGS)
Notre NGS se compose principalement d'un encodeur de texte, d'un encodeur géométrique, d'un module de raisonnement conjoint et d'un décodeur de programme. L'encodeur de texte est responsable de la représentation sémantique du texte de la question, et l'encodeur de figures géométriques est responsable de la représentation des figures géométriques. La représentation textuelle et la représentation graphique seront entrées dans le modèle de raisonnement commun pour la représentation sémantique multimodale et transmises au décodeur de programme pour le décodage du programme, et un programme de solution formelle interprétable et exécutable sera généré.
De plus, afin d'améliorer la capacité de représentation des figures géométriques par l'encodeur de figures géométriques et de promouvoir le module de raisonnement conjoint pour intégrer pleinement et exprimer efficacement les informations multimodales contenues dans la question, nous avons également introduit une variété de tâches auxiliaires pour améliorer les capacités de représentation du modèle et injecter des connaissances sur les théorèmes. Ces tâches auxiliaires comprennent : 1) Prédiction de la position du puzzle : la compréhension graphique des figures géométriques au niveau des pixels est obtenue en découpant les figures géométriques en plusieurs patchs, en les disposant de manière aléatoire, puis en laissant l'encodeur géométrique les réorganiser. 2) Prédiction des éléments géométriques : Laissez ; l'encodeur de figure géométrique apprend à prédire quels éléments géométriques apparaissent dans la figure géométrique actuelle pour obtenir une compréhension graphique au niveau de l'objet ; 3) Prédiction des points de connaissance : effectuer une fusion multimodale de la représentation du texte de la question et de la représentation de la figure géométrique dans le module de raisonnement commun ; En même temps, la tâche de classification des points de connaissance est introduite pour améliorer la représentation globale du problème. Dans NGS, nous pré-entraînons l'encodeur géométrique en utilisant la prédiction de position de puzzle et la prédiction d'éléments géométriques. La tâche de prédiction des points de connaissance est utilisée comme sous-tâche pour la formation multitâche avec NGS.
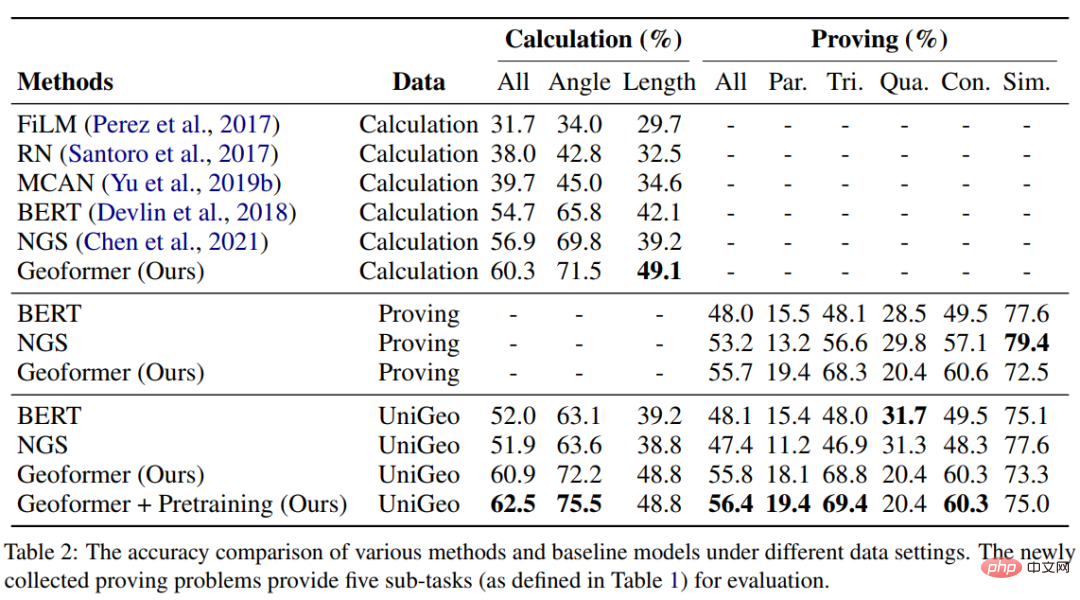
Dans l'expérience, l'article a construit plusieurs modèles de base basés sur des réseaux neuronaux basés sur GeoQA et a comparé NGS avec eux. Les résultats expérimentaux du NGS et des modèles de base sur GeoQA sont présentés dans le tableau ci-dessous.
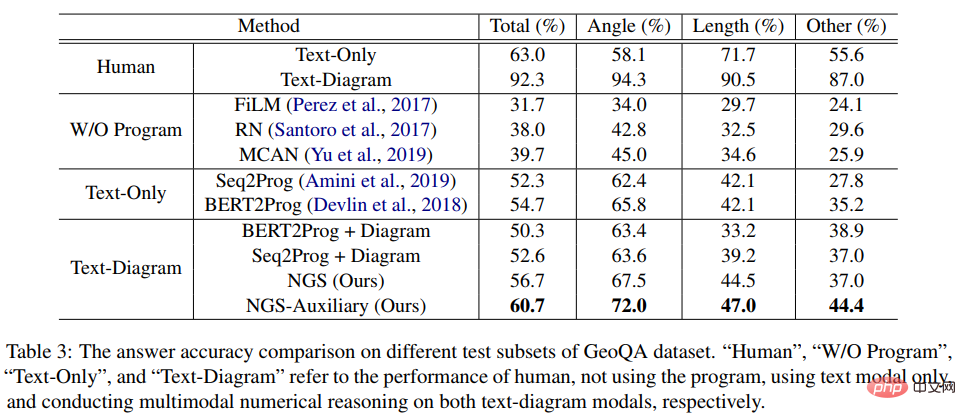
Comme le montre le tableau ci-dessus, NGS peut obtenir de meilleures performances de résolution de problèmes sur GeoQA que le modèle de base. Cependant, nous pouvons également constater qu’il existe encore un grand écart entre les différents modèles et les humains dans la résolution de problèmes géométriques.
De plus, nous avons également mené diverses expériences d'ablation pour vérifier l'efficacité de diverses conceptions en NGS. Pour plus de détails sur la recherche, veuillez vous référer à l’article original.
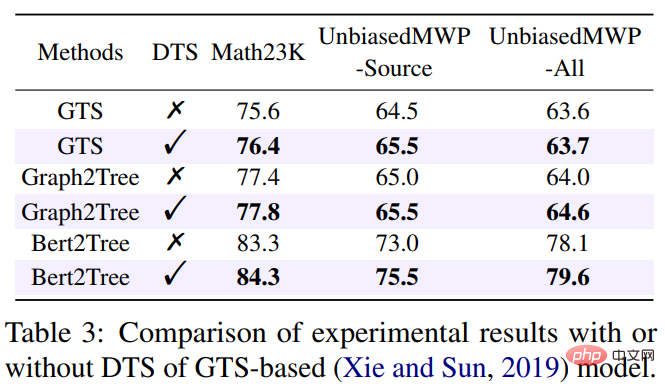
Papier 4 : Évaluation impartiale des problèmes de mots mathématiques pour atténuer les biais de résolution

Résultats de l'Association for Computational Linguistics : NAACL 2022
Adresse papier : https:/ /aclanthology.org/2022.findings-naacl.104.pdf
Dans ce travail, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'université Sun Yat-sen réexamine la méthode de résolution de problèmes d'évaluation du modèle sur le courant référence de résolution de problèmes d'application mathématiques Bias (résolution de biais). Ce biais de résolution de problèmes est principalement dû au biais de données et au biais d’apprentissage. Le biais des données fait référence au problème selon lequel l'ensemble de données de formation ne parvient pas à couvrir toutes les différentes méthodes narratives de chaque question. En conséquence, le modèle de résolution de problèmes ne peut apprendre que la sémantique superficielle et ne parvient pas à comprendre la sémantique profonde de la signification de la question, telle que. Comme le montre la figure 6 (a), étant donné que le modèle de résolution de problèmes n'apprend que la sémantique superficielle et l'utilise pour résoudre des problèmes, même après avoir supprimé la partie problématique du problème, le solutionneur de problèmes peut toujours atteindre 69,4 %.
Le biais d'apprentissage signifie qu'un MWP peut être résolu par plusieurs expressions équivalentes, mais les ensembles de données actuels n'utilisent qu'une des équations équivalentes comme étiquette, forçant le modèle à apprendre l'étiquette et à ignorer les autres équations équivalentes, ce qui conduit à un biais dans l’apprentissage de la formation. Comme le montre la figure 6 (b), au cours du processus de formation, le modèle peut générer une expression incompatible avec l'expression GroundTruth, mais la réponse est correcte. Cependant, comme l'ensemble de données utilise uniquement une certaine expression équivalente comme étiquette, il est utilisé. conduira à Lors du calcul de la fonction de perte, l'expression est considérée comme une expression incorrecte et la perte entre les deux expressions correctes est rétropropagée au modèle de solution, entraînant une surcorrection du modèle.

Figure 6 Exemples de biais de données et de biais d'apprentissage
Afin d'atténuer les biais dans les données, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'université Sun Yat-sen a fait une nouvelle tentative. Nous avons rebaptisé un nouveau benchmark MWP UnbiasedMWP de manière à couvrir autant que possible les questions posées. Nous avons collecté 2907 problèmes de mots comme questions de base, puis nous avons annoté autant de questions que possible pour les histoires contenues dans chaque question.
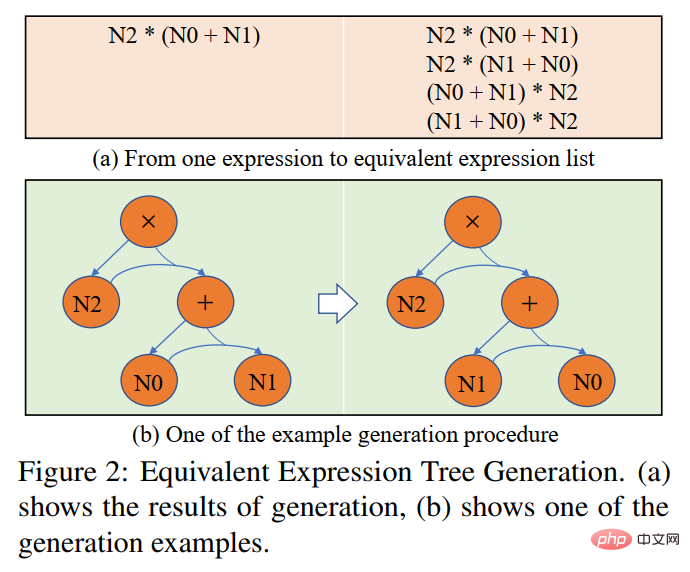
Afin de simplifier le processus d'annotation manuelle, nous générons d'abord des expressions raisonnables basées sur le contenu principal de la question, puis réécrivons la question à l'envers. Afin de générer des expressions raisonnables, nous avons conçu trois variantes d'expression : 1) Variante d'assortiment de variables (Va) : sélectionnez au hasard deux variables numériques dans l'épine dorsale de la question et utilisez des opérateurs mathématiques (+, -, *, /) Combinez-les, comme comme n0 + n1, n0 − n1, etc. 2) Transformation de sous-expression (Sub) : Toutes les sous-expressions contenues dans l'expression cible de la question d'origine sont modifiées par des opérateurs, obtenant ainsi une nouvelle expression. 3) Déformation d'expression entière (Whole) : obtenez une nouvelle expression en changeant les opérateurs contenus dans l'expression cible de la question d'origine. Les nouveaux ensembles d'expressions obtenus à partir des trois variantes ci-dessus sont filtrés manuellement, les expressions qui ne peuvent pas être annotées avec de nouvelles questions sont filtrées et les expressions restantes sont annotées manuellement avec des questions.
Afin d'atténuer le biais d'apprentissage, nous proposons une stratégie de sélection de cible dynamique Au cours du processus de formation, sur la base des résultats de la sortie du modèle, une expression cible plus proche de celle-ci est sélectionnée comme GroundTruth. Afin d'obtenir des expressions équivalentes, nous utilisons la loi commutative dans les opérations mathématiques pour déformer l'arbre d'expression afin d'obtenir plusieurs expressions équivalentes. Comme le montre la figure 7. Dans l'expérience, l'article a d'abord vérifié l'ensemble de données UnbiasedMWP sur plusieurs modèles de base SOTA. Les résultats expérimentaux sont présentés dans le tableau ci-dessous.
Il ressort des résultats expérimentaux que, par rapport au Math23K existant, notre ensemble de données UnbiasedMWP a moins de biais de données, car lorsque nous supprimons le problème de la question, les performances de la solution du modèle sont fortement réduites. du côté où notre ensemble de données est plus capable de faire en sorte que le modèle doive prêter attention aux informations sémantiques approfondies pour résoudre le problème. Afin de vérifier si notre stratégie de sélection dynamique de cibles peut réduire les biais d'apprentissage, nous avons appliqué la stratégie de sélection dynamique de cibles à plusieurs modèles de résolution de problèmes. Les résultats expérimentaux sont présentés dans le tableau ci-dessous.
Les résultats expérimentaux montrent que notre stratégie de sélection dynamique de cibles peut réduire efficacement le biais d'apprentissage et améliorer l'effet de solution du modèle. Pour plus de détails sur la recherche, veuillez vous référer à l’article original. 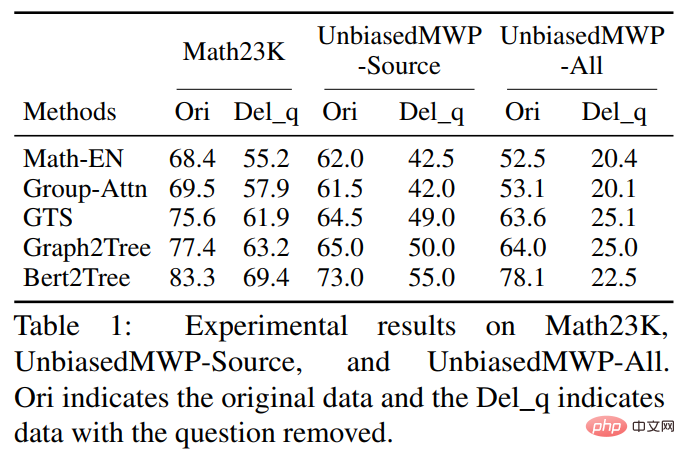
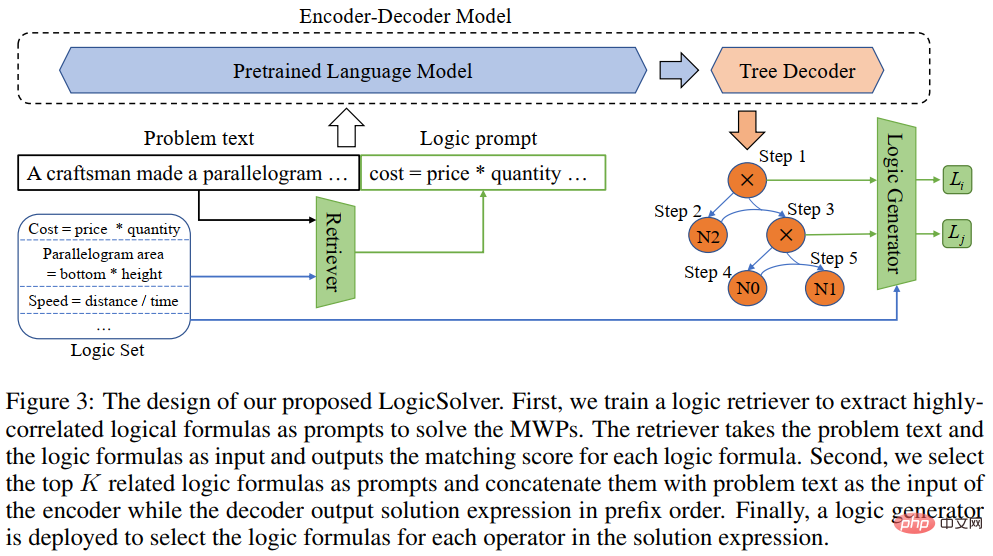
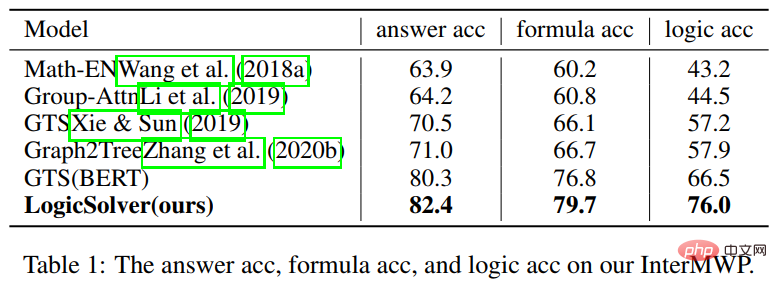
Article 5 : LogicSolver : Vers une résolution de problèmes de mots mathématiques interprétables avec un apprentissage amélioré par des invites logiques
Résultats de l'Association for Computational Linguistics : EMNLP 2022
Papier Adresse : https://arxiv.org/pdf/2205.08232.pdf

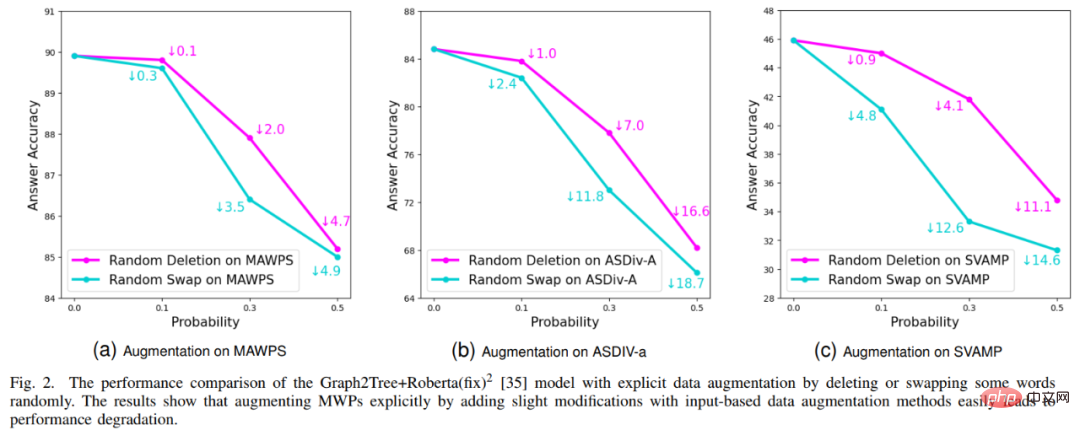
Ces dernières années, les modèles d'apprentissage profond ont obtenu un grand succès dans la résolution automatique de problèmes d'application mathématiques, notamment en termes de précision des réponses. Cependant, comme ces modèles utilisent uniquement des indices statistiques (heuristiques superficielles) pour obtenir des performances de résolution élevées et ne comprennent pas et ne raisonnent pas vraiment sur la logique mathématique derrière le problème, ces méthodes sont difficiles à expliquer. Afin de résoudre ce problème et de promouvoir le développement du domaine de la résolution de problèmes de mots mathématiques interprétables, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'Université Sun Yat-sen a construit le premier ensemble de données de problèmes de mots mathématiques expliqués de haute qualité, InterMWP. Cet ensemble de données contient 11 495 problèmes de mots mathématiques et 210 formules logiques basées sur des connaissances algébriques. L'expression de la solution de chaque problème de mots est annotée avec des formules logiques. Différent des ensembles de données de résolution de problèmes d'application mathématique existants, notre InterMWP nécessite non seulement que le résolveur de problèmes génère l'expression de résolution, mais exige également que le résolveur de problèmes génère l'expression logique basée sur les connaissances algébriques correspondant à l'expression de résolution, réalisant ainsi le modèle Explication de la sortie. Les similitudes et les différences entre l'ensemble de données InterMWP et d'autres ensembles de données de résolution de problèmes sont visibles dans la figure 8. Pour le processus d'annotation spécifique, veuillez vous référer au texte original. Figure 8 Exemple d'ensemble de données InterMWP Afin d'utiliser les connaissances en logique mathématique et de doter le solveur de problèmes MWP d'interprétabilité, notre équipe a ensuite construit une nouvelle solution de problème d'application mathématique, le framework LogicSolver. est illustré à la figure 9. Ce cadre extrait les connaissances logiques pertinentes de la bibliothèque de formules logiques sous forme d'informations rapides grâce à la récupération, améliorant ainsi la représentation sémantique du MWP par l'encodeur de questions et améliorant la capacité de génération de l'explication logique du MWP. Figure 9 Diagramme de conception de LogicSolver LogicSolver est principalement composé de trois composants principaux : un composant de récupération de connaissances logiques, un solveur MWP amélioré par invite logique et un composant de génération d'explications. Composant de récupération de connaissances logiques. Pour chaque MWP, nous récupérons les k formules logiques hautement pertinentes à partir de 210 formules logiques comme indices pour améliorer la résolution de MWP. Nous connectons les invites de formule logique au texte de la question en entrée pour piloter le modèle MWP afin de générer des expressions de solution. Enfin, pour obtenir des explications basées sur des formules logiques, nous déployons un générateur logique pour prédire la formule logique correspondant à chaque nœud interne (c'est-à-dire l'opérateur) de l'arbre d'expression logique comme explication de la solution. Au cours des expériences, nous avons construit plusieurs modèles de base sur l'ensemble de données InterMWP et comparé notre LogicSolver avec ces modèles de base. Les résultats expérimentaux sont présentés dans le tableau ci-dessous. Les résultats expérimentaux montrent que notre LogicSolver peut être amélioré en termes de précision des réponses, de précision des formules et de précision des formules logiques, ce qui montre que notre LogicSolver améliore les performances de résolution (Answer Acc et Formula Acc) tout en avoir une meilleure interprétabilité logique (Logic Acc). Pour plus de détails sur la recherche, veuillez vous référer à l’article original. Article 6 : UniGeo : Unifier le raisonnement logique de la géométrie via la reformulation de l'expression mathématique Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen et Xiaodan Liang La Conférence 2022 sur les méthodes empiriques dans le traitement du langage naturel La résolution automatique de problèmes de géométrie est une référence pour évaluer les capacités de raisonnement multimodal des modèles profonds. Cependant, dans la plupart des travaux existants, la solution automatique des problèmes de calcul géométrique et la preuve automatique des problèmes géométriques sont considérées comme deux tâches différentes, et des traitements d'annotation différents sont appliqués, ce qui entrave le raisonnement unifié des modèles profonds dans les différentes tâches de recherche mathématique. Essentiellement, les questions de calcul géométrique et les questions de preuve géométrique ont des expressions de problèmes similaires et les connaissances mathématiques requises pour les résoudre se chevauchent également. Par conséquent, une représentation et un apprentissage unifiés des deux tâches de résolution automatique de problèmes de calcul géométrique et de résolution automatique de problèmes géométriques peuvent aider à améliorer la compréhension sémantique et le raisonnement symbolique des modèles profonds pour ces deux problèmes. À cette fin, l'équipe du laboratoire de fusion d'intelligence humaine-machine de l'université Sun Yat-sen a construit UniGeo, un ensemble de données de référence contenant des milliers de questions géométriques. UniGeo comprend 4 998 problèmes de calcul géométrique et 9 543 problèmes de preuve géométrique. Nous fournissons des annotations de preuve en plusieurs étapes pour chaque problème de preuve, et ces annotations peuvent être facilement converties en programmes symboliques exécutables. Les questions de calcul utilisent également des annotations similaires, comme le montre la figure 10. Après annotation comme le montre la figure 10, UniGeo peut bien représenter des problèmes de calcul géométrique et des problèmes de preuve géométrique dans un langage symbolique formel. Figure 10 Échantillon de données UniGeo Après avoir utilisé un langage symbolique formel pour annoter uniformément les questions de calcul géométrique et les questions de preuve géométrique, afin de vérifier la capacité de représentation unifiée de ces deux questions. favorise la compréhension sémantique du modèle et la capacité de raisonnement symbolique pour les problèmes de calcul géométrique et les problèmes de preuve géométrique, obtenant ainsi des solutions plus efficaces aux problèmes de calcul et de preuve. L'équipe du laboratoire d'intégration intelligente homme-machine-objet de l'université Sun Yat-sen a construit Geoformer pour un traitement unifié de la résolution de problèmes géométriques et de la preuve afin de gérer simultanément les problèmes de calcul géométrique et les problèmes de preuve géométrique, comme le montre la figure 11. Figure 11 Schéma du GeoFormer De plus, afin d'apprendre un Geoformer efficace pour parvenir à un raisonnement géométrique unifié, l'équipe du Laboratoire d'intégration de l'intelligence humaine-machine de l'Université Sun Yat-sen a en outre proposé prédiction d'expression mathématique Les tâches de formation, combinées aux tâches MLM, effectuent une pré-formation aux tâches sur Geoformer, comme le montre la figure 12. Dans l'expérience, nous avons construit plusieurs modèles de base basés sur le benchmark UniGeo et comparé les performances de notre GeoFormer proposé. Les résultats expérimentaux sont présentés dans le tableau ci-dessous. Comme le montrent les résultats expérimentaux, le GeoFormer que nous avons proposé peut atteindre de meilleures performances globales que le modèle de base sur les sous-ensembles de données du problème de calcul et de preuve. De même, GeoFormer est supérieur aux modèles de base NGS et BERT sur l'ensemble complet de données qui nécessitent une solution unifiée des problèmes de calcul et de preuve. Après la pré-formation aux expressions mathématiques et la pré-formation MLM, GeoFormer+Pretraining bénéficiera d'améliorations supplémentaires en termes de performances par rapport à GeoFormer. Ces résultats expérimentaux prouvent pleinement l'efficacité de GeoFormer et illustrent également que le raisonnement par modèle unifié pour les problèmes de calcul géométrique et les problèmes de preuve géométrique est également utile pour leurs tâches respectives. Ce travail a été inclus dans la conférence principale de l'EMNLP2022, veuillez rester à l'écoute pour plus de détails sur la recherche. Pas 7 : Pré-formation à la distillation contrastive basée sur un modèle pour la résolution de problèmes de mots mathématiques Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang et Liang Lin Bien que profond Les modèles d'apprentissage ont fait de bons progrès dans le domaine de la résolution de problèmes mathématiques, mais ces modèles ignorent la logique de solution contenue dans la description du problème, et cette logique de résolution de problèmes peut souvent correspondre au modèle de problème (solution). Comme le montre la figure 13, deux problèmes de mots différents peuvent chacun correspondre à la même solution.
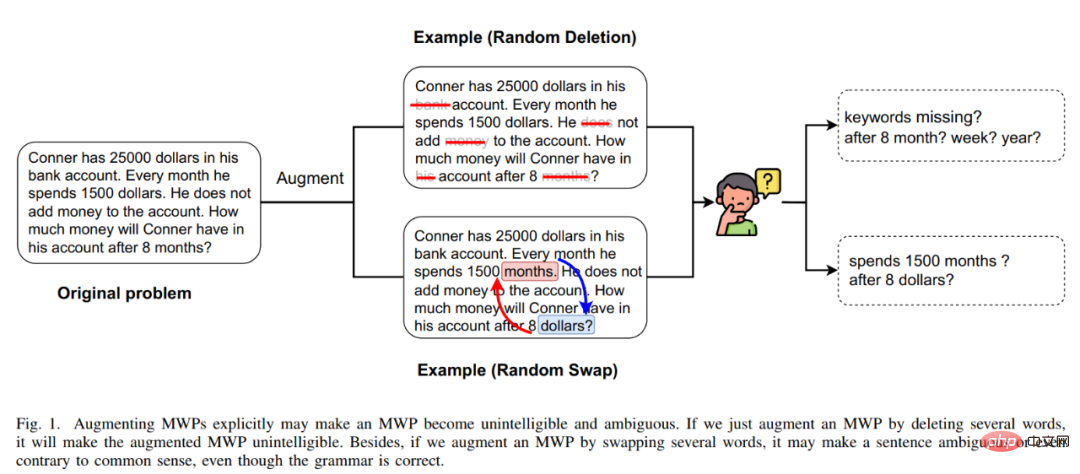
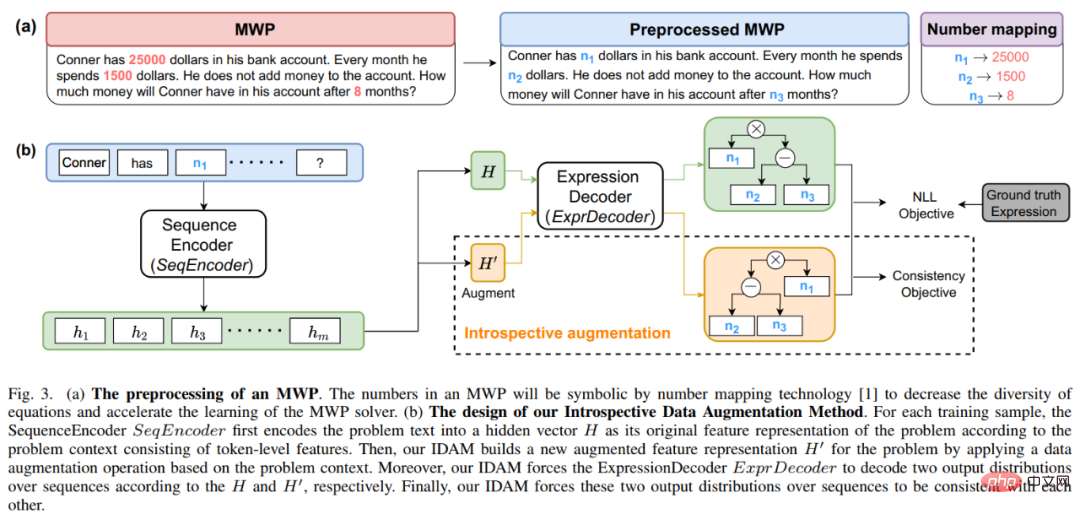
Figure 13 Exemples de problèmes de mots avec des descriptions de langues différentes mais la même solution De plus, les modèles linguistiques pré-entraînés (PLM) contiennent des connaissances riches et ont la capacité d'avoir une représentation sémantique de haute qualité, ce qui sera utile pour résoudre les problèmes MWP. Afin d'utiliser pleinement les riches connaissances contenues dans le modèle de langage pré-entraîné et d'utiliser la logique de solution pour résoudre plus efficacement les problèmes d'application, l'équipe du laboratoire d'intégration de l'intelligence humaine-machine de l'université Sun Yat-sen a proposé une distillation comparative basé sur des modèles de solution et des modèles de langage pré-entraînés. La méthode de pré-entraînement effectue un pré-entraînement de domaine sur l'encodeur de problème dans le solveur, comme le montre la figure 14. Cette méthode utilise un apprentissage contrastif multiperspectif pour prendre en compte efficacement les connaissances en logique mathématique tout en utilisant la distillation des connaissances pour conserver efficacement les connaissances et les capacités de représentation sémantique de haute qualité dans le modèle de langage pré-entraîné. Plus précisément, nous utilisons d'abord si les modèles de solutions entre les deux questions sont cohérents comme signe pour déterminer si les deux questions doivent être proches l'une de l'autre dans l'espace de représentation. Ensuite, nous proposons un apprentissage comparatif multiperspectif, qui implique un apprentissage comparatif à partir des encodeurs de l'enseignant, des encodeurs des élèves et de leurs encodeurs Momentum correspondants, de sorte que deux représentations de questions avec le même modèle de solution puissent interagir entre elles dans l'espace de représentation de l'enseignant et dans celui de l'élève. L'espace. Rapprochez-vous pour réaliser l'injection de la logique de la solution. De plus, afin de conserver autant que possible les connaissances et les capacités de représentation de haute qualité contenues dans l'encodeur étudiant initialisé avec un modèle de langage pré-entraîné, nous utilisons la distillation des connaissances pour contraindre la représentation de l'encodeur étudiant en utilisant la représentation des fonctionnalités. de l'encodeur enseignant comme supervision Avoir les mêmes capacités de représentation que l'encodeur enseignant formé, réalisant ainsi la préservation sémantique. Figure 14 Méthode de pré-entraînement par distillation comparative basée sur un modèle de solution et un modèle de langage pré-entraîné Dans l'expérience, nous utilisons différents modèles de langage pré-entraînés comme initialisation et vérifions notre méthode Effet. Nous initialisons l'encodeur de problème MathEncoder avec les poids de base BERT et de base Roberta respectivement, et utilisons le décodeur dans GTS comme décodeur d'expression. Nous appelons collectivement les solveurs basés sur MathEncoder MathSolver. Nous avons comparé MathSolver avec plusieurs méthodes sur Math23K et CM17K. Les résultats expérimentaux sont présentés dans le tableau ci-dessous. Comme le montrent les résultats expérimentaux, la méthode que nous avons proposée peut améliorer efficacement la capacité de résolution de problèmes du solveur et peut être appliquée sur une variété de différents modèles de langage pré-entraînés. Les résultats ont été soumis à IEEE Transactions on Neural Networks and Learning Systems, veuillez rester à l'écoute pour plus de détails. Papier 8 : Une méthode introspective d'augmentation des données pour former des résolveurs de problèmes de mots mathématiques Jinghui Qin, Zhongzhan Huang, Ying Zeng et Liang Lin Ces dernières années, de plus en plus de chercheurs a commencé à étudier des méthodes basées sur l'apprentissage en profondeur pour résoudre automatiquement les problèmes d'application mathématique, car la résolution automatique de problèmes d'application mathématique peut démontrer pleinement le degré d'intelligence machine. Étant donné que l'annotation d'ensembles de données MWP de haute qualité et à grande échelle est très coûteuse, par exemple en exigeant des connaissances professionnelles avec des niveaux d'éducation correspondants et des données de questions accessibles à grande échelle, l'échelle des ensembles de données MWP existants de haute qualité n'est pas suffisante pour former un MWP efficace. solution. Les machines à questions ne suffisent pas. Le problème de goulot d'étranglement des données de MWP nous encourage à réfléchir à la manière d'utiliser des méthodes d'augmentation de données rentables pour améliorer l'efficacité de l'utilisation des données et améliorer les performances du solveur. La méthode d'amélioration des données la plus directe est la méthode d'amélioration des données basée sur la saisie, telle que le remplacement de caractères couramment utilisés, la suppression de caractères, etc. Cependant, ce type de méthode ne convient pas à MWP, car MWP présente les caractéristiques de concision et de concision, ce qui perturbera le texte saisi. Ou une modification peut rendre le sens de la question flou. De plus, la relation mathématique contenue dans le sens de la question ne peut pas être modifiée, mais ce type de méthode est susceptible de modifier la relation mathématique contenue dans le sens de la question, comme le montre la figure 15. Figure 15 Exemple de méthode d'augmentation des données basée sur la saisie qui ne convient pas aux tâches MWP De plus, l'équipe du laboratoire de fusion d'intelligence homme-machine-objet de l'Université Sun Yat-sen a également mené des recherches sur la méthode d'augmentation des données basée sur les entrées Certaines vérifications, les résultats expérimentaux sont présentés dans la figure 16. Les résultats expérimentaux montrent que la méthode d'augmentation explicite des données basée sur les entrées n'est pas applicable à la tâche MWP et ne peut pas atténuer efficacement le problème de goulot d'étranglement des données rencontré par la tâche MWP. Figure 16 La méthode d'amélioration des données basée sur les entrées ne peut pas améliorer l'effet de résolution de problèmes MWP Pour cette raison, nous proposons une méthode d'amélioration des données simple et efficace adaptée aux données MWP - introspection La méthode intégrée d'augmentation des données (IDAM) améliore la représentation de la question dans l'espace latent pendant le processus de formation, résolvant ainsi les problèmes rencontrés par les méthodes d'augmentation des données basées sur les entrées dans les tâches de résolution de MWP. La méthode IDAM met en œuvre différentes méthodes de construction de représentation (regroupement de moyennes, agrégation hiérarchique, élimination aléatoire, échange aléatoire, etc.) en codant la représentation du problème pour obtenir une nouvelle représentation du problème, puis utilise la fonction objectif de cohérence (basée sur l'expression entre divergence JS) pour contraindre la sortie de décodage d'expression du solveur basée sur la nouvelle représentation du problème à être cohérente avec la sortie de décodage d'expression basée sur la représentation originale du problème. Un diagramme schématique de la méthode est présenté à la figure 17. Figure 17 Diagramme schématique de la méthode d'augmentation introspective des données (IDAM) Dans l'expérience, nous avons intégré IDAM dans plusieurs méthodes SOTA et les avons comparées sur plusieurs ensembles de données, ce qui vérifie la l'efficacité et la polyvalence de notre méthode IDAM. Les résultats expérimentaux sont présentés dans le tableau ci-dessous. Les résultats expérimentaux montrent que, dans la même configuration expérimentale, notre IDAM peut améliorer les performances de différents modèles de base de solveurs sur différents ensembles de données MWP. Cela illustre pleinement l’efficacité de notre approche IDAM sur le problème MWP. Ce résultat a été soumis aux transactions IEEE/ACM sur le traitement de l'audio, de la parole et du langage, veuillez rester à l'écoute pour plus de détails. Introduction au laboratoire Le Laboratoire de convergence de l'intelligence humaine-machine (HCP Lab) de l'Université Sun Yat-sen a été fondé par le professeur Lin Li en 2010. Il se concentre sur des sujets de recherche sur les technologies de pointe en matière d'intelligence artificielle et a remporté le premier prix en science et technologie de la Société chinoise de l'image et du graphisme, le prix Wu Wenjun des sciences naturelles, le premier prix provincial en sciences naturelles et d'autres distinctions ; il a formé de jeunes talents de niveau national tels que Liang Xiaodan et Wang Keze ; . 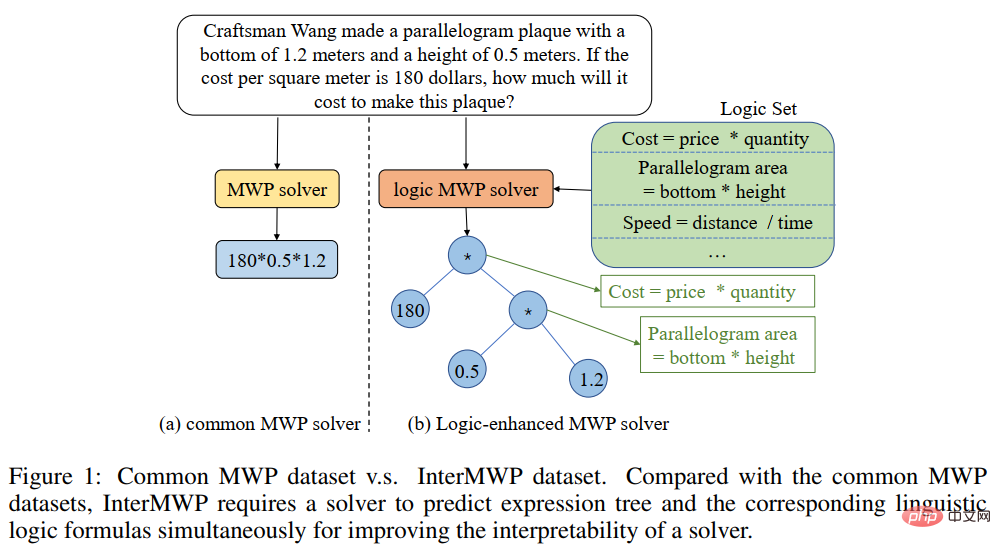
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Traiter efficacement 7 millions d'enregistrements et créer des cartes interactives avec la technologie géospatiale. Cet article explore comment traiter efficacement plus de 7 millions d'enregistrements en utilisant Laravel et MySQL et les convertir en visualisations de cartes interactives. Exigences initiales du projet de défi: extraire des informations précieuses en utilisant 7 millions d'enregistrements dans la base de données MySQL. Beaucoup de gens considèrent d'abord les langages de programmation, mais ignorent la base de données elle-même: peut-il répondre aux besoins? La migration des données ou l'ajustement structurel est-il requis? MySQL peut-il résister à une charge de données aussi importante? Analyse préliminaire: les filtres et les propriétés clés doivent être identifiés. Après analyse, il a été constaté que seuls quelques attributs étaient liés à la solution. Nous avons vérifié la faisabilité du filtre et établi certaines restrictions pour optimiser la recherche. Recherche de cartes basée sur la ville
 Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Il existe de nombreuses raisons pour lesquelles la startup MySQL échoue, et elle peut être diagnostiquée en vérifiant le journal des erreurs. Les causes courantes incluent les conflits de port (vérifier l'occupation du port et la configuration de modification), les problèmes d'autorisation (vérifier le service exécutant les autorisations des utilisateurs), les erreurs de fichier de configuration (vérifier les paramètres des paramètres), la corruption du répertoire de données (restaurer les données ou reconstruire l'espace de la table), les problèmes d'espace de la table InNODB (vérifier les fichiers IBDATA1), la défaillance du chargement du plug-in (vérification du journal des erreurs). Lors de la résolution de problèmes, vous devez les analyser en fonction du journal d'erreur, trouver la cause profonde du problème et développer l'habitude de sauvegarder régulièrement les données pour prévenir et résoudre des problèmes.
 Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
L'article présente le fonctionnement de la base de données MySQL. Tout d'abord, vous devez installer un client MySQL, tel que MySQLWorkBench ou le client de ligne de commande. 1. Utilisez la commande MySQL-UROot-P pour vous connecter au serveur et connecter avec le mot de passe du compte racine; 2. Utilisez Createdatabase pour créer une base de données et utilisez Sélectionner une base de données; 3. Utilisez CreateTable pour créer une table, définissez des champs et des types de données; 4. Utilisez InsertInto pour insérer des données, remettre en question les données, mettre à jour les données par mise à jour et supprimer les données par Supprimer. Ce n'est qu'en maîtrisant ces étapes, en apprenant à faire face à des problèmes courants et à l'optimisation des performances de la base de données que vous pouvez utiliser efficacement MySQL.
 Les ingénieurs de backend senior à distance (plates-formes) ont besoin de cercles
Apr 08, 2025 pm 12:27 PM
Les ingénieurs de backend senior à distance (plates-formes) ont besoin de cercles
Apr 08, 2025 pm 12:27 PM
Ingénieur backend à distance Emploi Vacant Société: Emplacement du cercle: Bureau à distance Type d'emploi: Salaire à temps plein: 130 000 $ - 140 000 $ Description du poste Participez à la recherche et au développement des applications mobiles Circle et des fonctionnalités publiques liées à l'API couvrant l'intégralité du cycle de vie de développement logiciel. Les principales responsabilités complètent indépendamment les travaux de développement basés sur RubyOnRails et collaborent avec l'équipe frontale React / Redux / Relay. Créez les fonctionnalités de base et les améliorations des applications Web et travaillez en étroite collaboration avec les concepteurs et le leadership tout au long du processus de conception fonctionnelle. Promouvoir les processus de développement positifs et hiérarchiser la vitesse d'itération. Nécessite plus de 6 ans de backend d'applications Web complexe
 Mysql peut-il renvoyer JSON
Apr 08, 2025 pm 03:09 PM
Mysql peut-il renvoyer JSON
Apr 08, 2025 pm 03:09 PM
MySQL peut renvoyer les données JSON. La fonction JSON_Extract extrait les valeurs de champ. Pour les requêtes complexes, envisagez d'utiliser la clause pour filtrer les données JSON, mais faites attention à son impact sur les performances. Le support de MySQL pour JSON augmente constamment, et il est recommandé de faire attention aux dernières versions et fonctionnalités.
 La clé principale de MySQL peut être nul
Apr 08, 2025 pm 03:03 PM
La clé principale de MySQL peut être nul
Apr 08, 2025 pm 03:03 PM
La clé primaire MySQL ne peut pas être vide car la clé principale est un attribut de clé qui identifie de manière unique chaque ligne dans la base de données. Si la clé primaire peut être vide, l'enregistrement ne peut pas être identifié de manière unique, ce qui entraînera une confusion des données. Lorsque vous utilisez des colonnes entières ou des UUIdes auto-incrémentales comme clés principales, vous devez considérer des facteurs tels que l'efficacité et l'occupation de l'espace et choisir une solution appropriée.
 MySQL ne peut pas être installé après le téléchargement
Apr 08, 2025 am 11:24 AM
MySQL ne peut pas être installé après le téléchargement
Apr 08, 2025 am 11:24 AM
Les principales raisons de la défaillance de l'installation de MySQL sont les suivantes: 1. Problèmes d'autorisation, vous devez s'exécuter en tant qu'administrateur ou utiliser la commande sudo; 2. Des dépendances sont manquantes et vous devez installer des packages de développement pertinents; 3. Conflits du port, vous devez fermer le programme qui occupe le port 3306 ou modifier le fichier de configuration; 4. Le package d'installation est corrompu, vous devez télécharger et vérifier l'intégrité; 5. La variable d'environnement est mal configurée et les variables d'environnement doivent être correctement configurées en fonction du système d'exploitation. Résolvez ces problèmes et vérifiez soigneusement chaque étape pour installer avec succès MySQL.
 Comprendre les propriétés acides: les piliers d'une base de données fiable
Apr 08, 2025 pm 06:33 PM
Comprendre les propriétés acides: les piliers d'une base de données fiable
Apr 08, 2025 pm 06:33 PM
Une explication détaillée des attributs d'acide de base de données Les attributs acides sont un ensemble de règles pour garantir la fiabilité et la cohérence des transactions de base de données. Ils définissent comment les systèmes de bases de données gérent les transactions et garantissent l'intégrité et la précision des données même en cas de plantages système, d'interruptions d'alimentation ou de plusieurs utilisateurs d'accès simultanément. Présentation de l'attribut acide Atomicité: une transaction est considérée comme une unité indivisible. Toute pièce échoue, la transaction entière est reculée et la base de données ne conserve aucune modification. Par exemple, si un transfert bancaire est déduit d'un compte mais pas augmenté à un autre, toute l'opération est révoquée. BeginTransaction; UpdateAccountSsetBalance = Balance-100Wh





