 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Michael Bronstein s'inspire de la topologie algébrique et propose une nouvelle structure informatique de réseau neuronal graphique !
Michael Bronstein s'inspire de la topologie algébrique et propose une nouvelle structure informatique de réseau neuronal graphique !
Michael Bronstein s'inspire de la topologie algébrique et propose une nouvelle structure informatique de réseau neuronal graphique !
Cet article est co-écrit par Cristian Bodnar et Fabrizio Frasca, et publié par C. Bodnar, F. Frasca et autres dans 2021 ICML "Weisfeiler and Lehman Go Topological: Information Transfer Simple Network" et 2021 NeurIPS "Weisfeiler and Lehman Go Topological: Information Transfer Simple Network" Cellulaire : CW Network" 》Le document est utilisé comme référence.
Cet article n'est qu'une partie de la discussion sur les séries de réseaux neuronaux graphiques du point de vue de la géométrie différentielle et de la topologie algébrique.
Les graphiques peuvent être utilisés pour simuler n'importe quoi, des réseaux informatiques aux interactions de particules dans le Grand collisionneur de hadrons. Les graphiques sont omniprésents en raison de leur nature discrète et combinatoire, qui leur permet d'exprimer des relations abstraites tout en étant faciles à calculer. L'une des raisons de leur popularité est que les graphiques font abstraction de la géométrie, c'est-à-dire de l'endroit où se trouvent les nœuds dans l'espace ou de la façon dont les bords sont courbés, ne laissant qu'une représentation de la façon dont les nœuds sont connectés.
La théorie des graphes est née de l'observation de Leonhard Euler dans son livre de 1741 "Geometria situs" selon laquelle il n'y avait pas de solution au célèbre problème des sept ponts de Königsberg.
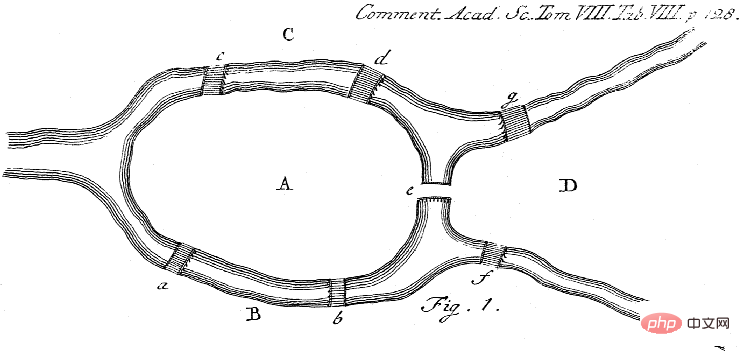
Illustration : Le problème des sept ponts nécessite de trouver un itinéraire de randonnée circulaire dans la ville de Königsberg sans traverser plusieurs fois le pont. Comme le disait Euler, la forme exacte de la ville de Königsberg n'a pas d'importance, ce qui compte c'est la façon dont les différentes parcelles de terrain (nœuds du graphique) sont reliées les unes aux autres (bords). Euler a montré qu'un tel cycle existe si et seulement si tous les nœuds ont un degré pair. De plus, seuls cinq des ponts d’origine ont survécu jusqu’à l’époque moderne. Source : Wikipédia
Fait intéressant, la découverte d'Euler a non seulement marqué le début de la théorie des graphes, mais est aussi souvent considérée comme la naissance de la topologie. Comme pour les graphiques, les topologues s’intéressent aux propriétés d’un espace indépendantes de sa forme ou de sa géométrie spécifique.
L'expression moderne de ces idées est apparue en 1895 dans "Analysis situs", un article fondateur d'Henri Poincaré, dont les travaux ont suscité l'intérêt pour la description combinatoire des variétés, de Les invariants topologiques peuvent être trouvés et calculés plus facilement dans ces variétés .
Légende : Leonhard Euler (1707-1783) et Henri Poincaré (1854-1912)
Ces descriptions combinatoires sont aujourd'hui appelées complexes cellulaires et peuvent être considérées comme des dimensions supérieures du graphe Généralisation .
Contrairement aux graphes formés par des nœuds et des arêtes, les complexes cellulaires peuvent également contenir des structures de dimension supérieure ou « cellules » : les sommets sont des cellules 0, les arêtes sont des cellules 1, les surfaces 2D sont des cellules 2, etc. Pour construire un complexe cellulaire, nous pouvons le superposer en collant les limites d’une cellule à d’autres cellules de dimension inférieure.
Dans des cas particuliers, lorsque les cellules sont composées de simplexes (comme des arêtes, des triangles, des tétraèdres, etc.), ces espaces sont également appelés complexes simplexes.

Légende : Un graphe peut être vu comme un ensemble de sommets auxquels nous attachons des arêtes (1 cellule). De même, les complexes unicellulaires et les complexes cellulaires peuvent être visualisés sous forme de graphiques dans lesquels nous connectons 2 cellules (indiquées en bleu), 3 cellules (indiquées en vert), etc.
1 Topologie dans l'apprentissage automatique et la science des données
Nous pensons qu'il n'est pas nécessaire d'attendre 400 ans pour que la topologie devienne un outil pratique.
Les structures topologiques telles que les complexes peu profonds ont été utilisées dans l'apprentissage automatique et la science des données sous l'égide de l'analyse de données topologiques (TDA). Ce type de méthode est apparu dans les années 1990 pour tenter de mesurer de manière insensible et robuste au bruit. pour analyser la « forme des données ».
Les racines du TDA remontent aux travaux de l'un des topologues les plus prolifiques, Léopold Vietnam Oris, à la fin des années 1920. Cependant, ces technologies ont dû attendre l’avènement de l’informatique moderne avant de pouvoir être appliquées à grande échelle.

Légende : Etant donné un nuage de points, l'intersection entre des sphères fermées de rayon fixe autour de chaque point produit un complexe simple. En augmentant progressivement le rayon de la sphère, on peut obtenir une séquence emboîtée de complexes simples. Source de l'image : Bastian Rieck.
Le cheval de bataille de TDA est l'homologie persistante (PH), une méthode d'extraction de caractéristiques topologiques à partir de nuages de points. Étant donné un ensemble de données de points, PH crée une séquence imbriquée de nombres complexes simples, où chaque nombre complexe correspond à une certaine échelle du nuage de points sous-jacent en cours d'analyse. Il suit ensuite diverses caractéristiques topologiques (par exemple, composants connectés, boucles ou trous) qui apparaissent et disparaissent à mesure que l'échelle augmente progressivement et que l'on passe d'un complexe de la séquence au suivant.
À l'ère de l'apprentissage profond, l'homologie persistante a eu une "seconde vie" car il a été démontré que l'on pouvait effectuer une rétropropagation à travers elle, permettant l'intégration de dispositifs TDA déjà établis dans des cadres d'apprentissage profond.
Un corpus de travaux récent propose différentes utilisations des simplifications et des complexes cellulaires dans l'apprentissage profond géométrique, en tant qu'espace topologique sous-jacent plus riche pour prendre en charge les données et les calculs effectués dessus.
Plusieurs des premiers travaux visant à exploiter cette perspective proposaient des modèles convolutifs et des méthodes de marche aléatoire fonctionnant sur des complexes simplifiés. Comme dans cet article, les modèles convolutifs peuvent être compris comme des exemples simples et concrets de transfert d’informations sur des complexes de cellules.
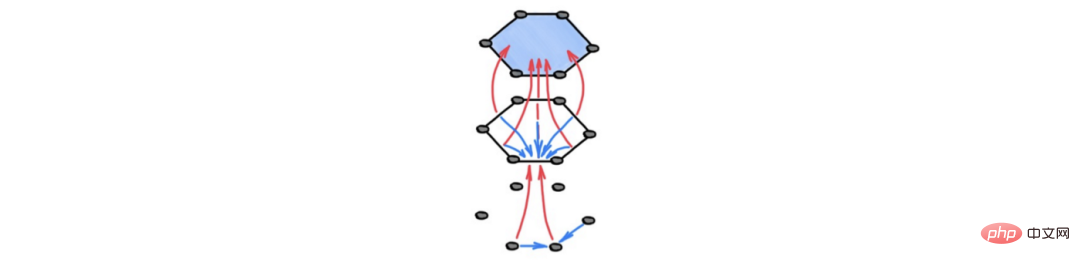
Étant donné que le calcul est piloté par la structure topologique de ces espaces (c'est-à-dire la structure du quartier), nous appelons cette méthode le transfert d'informations topologiques. Dans ce cadre, des unités adjacentes, éventuellement de dimensions différentes, échangent des informations, comme le montre la figure ci-dessous.
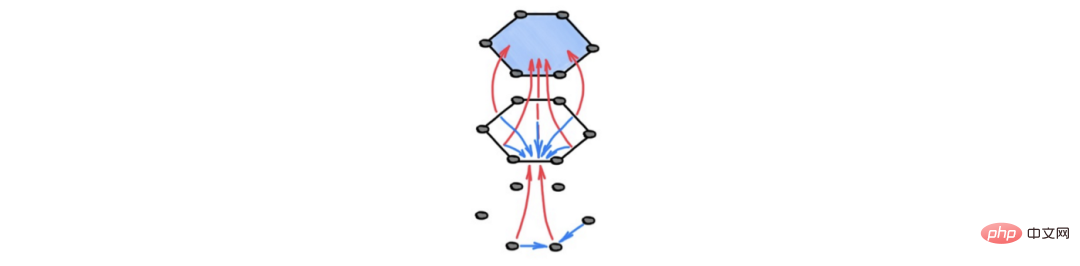
Légende : Diagramme schématique du transfert d'informations topologiques. Les flèches bleues décrivent la propagation « horizontale » de l'information entre des cellules adjacentes dans la couche supérieure, c'est-à-dire des cellules situées aux limites d'une même cellule de grande dimension. La flèche rouge représente la propagation « verticale » des informations, où une cellule reçoit des informations provenant de cellules de dimension inférieure situées à ses frontières. Ce calcul peut être interprété comme une forme d'ensemble (différentiable) en résumant les informations des cellules limites dans une représentation plus grossière.
Au-delà des graphiques dans les GNN
Bien que les complexes cellulaires fournissent une structure riche, nous ne pouvons ignorer que les graphiques sont de loin les objets topologiques les plus courants dans l'apprentissage automatique, et que peu d'ensembles de données les surpassent. Néanmoins, on peut toujours exploiter ces espaces topologiques intéressants en transformant le graphe d'entrée.
Nous appelons la conversion d'un graphe en un espace topologique de grande dimension "lifting", pour ressembler au concept du même nom dans la théorie des catégories. Il s'agit d'une transformation qui ajoute des cellules de grande dimension au graphique d'entrée en suivant certaines règles. Par exemple, un graphe peut être promu en complexe cellulaire en attachant une cellule de dimension supérieure à chaque falaise ou cycle du graphe. En faisant cela, le graphe est remplacé par un espace différent qui a plus de structure et peut fournir au GNN une meilleure structure de calcul que le graphe d'origine. Ci-dessous, nous discutons des avantages spécifiques de cette approche.
Légende : En collant les limites d'un disque fermé bidimensionnel aux boucles induites dans le graphique, des complexes cellulaires de grande dimension peuvent être construits à partir du graphique.
Caractéristiques et structures d'ordre élevé
GNN adopte généralement une vue centrée sur les nœuds, et les données résidant sur les bords ne sont considérées que comme des informations auxiliaires pour augmenter la communication entre les sommets. Dans le transfert d'informations topologiques, toutes les unités sont des citoyens de première classe. Quelles que soient leurs dimensions, ils se voient attribuer une représentation spécifique, élaborée par échange d'informations avec les unités voisines. Cela fournit une recette pour modéliser explicitement certaines structures d’ordre supérieur et les interactions entre elles. En particulier, il fournit une approche de principe pour faire évoluer les caractéristiques de bord (c'est-à-dire 1 unité) du graphe d'entrée, ce qui est un problème qu'une grande classe de modèles GNN ne prend pas en compte.
Interactions d'ordre supérieurLes diagrammes sont par définition binaires ("par paires") et ne peuvent pas représenter des relations et des interactions impliquant plus de deux objets. Cela peut poser un problème lors de la modélisation de systèmes complexes caractérisés par des interactions d'ordre supérieur : par exemple, trois réactifs dans une réaction chimique peuvent interagir simultanément. Dans un complexe cellulaire, cette situation peut être codée en connectant des réactifs entre deux cellules (c'est-à-dire un triangle « rempli »). Par conséquent, le flux de calcul du modèle est adapté à la présence d’interactions d’ordre supérieur.
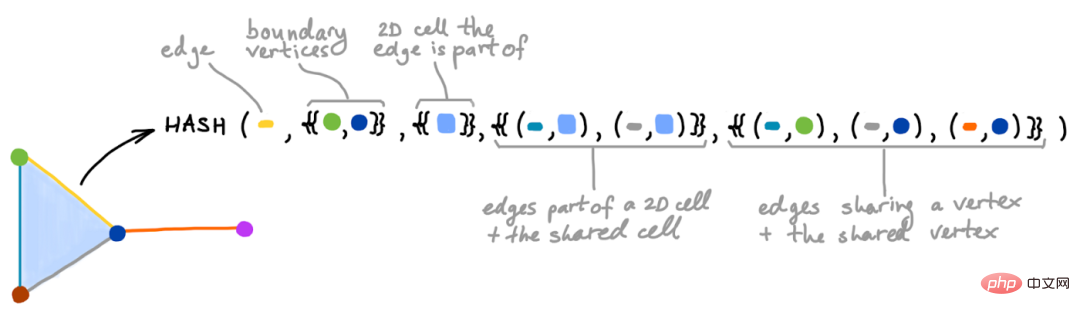
Légende : Test Cell Weisfeiler-Lehman (CWL), étendant le test WL classique aux populations cellulaires, chaque étape de l'algorithme hache parfaitement les couleurs des cellules adjacentes (il peut y avoir des dimensions différentes).
ExpressivitéLe pouvoir expressif des informations transmettant les GNN est limité par le test d'isomorphisme des graphes de Weisfeiler-Leman (WL). On sait que WL ne peut pas détecter certaines sous-structures de graphes, telles que les triangles ou les cycles, même très simples. - Les images isomorphes sont également indiscernables.
Selon des articles précédents (adresse papier : https://arxiv.org/abs/2103.03212; https://arxiv.org/abs/2106.12575), Test WL (CWL) Le cellulaire La version peut être utilisée pour tester l'isomorphisme des complexes cellulaires. Lorsque ce nouveau test est associé à la procédure de levage de graphes décrite ci-dessus, il s'avère qu'il peut distinguer des classes de graphes plus grandes que le test WL. Ainsi, sous certaines conditions, le processus de transfert d’informations topologiques hérite des avantages de ce test et améliore la capacité d’expression par rapport au GNN standard. Inadéquat, lissage excessif et goulots d'étranglement
GNN pour le transfert d'informations nécessite n couches pour permettre aux nœuds distants de n sauts de communiquer. Lorsque seules quelques couches sont utilisées afin que les nœuds éloignés ne puissent pas échanger d'informations
, ce phénomène est appelé sous-portée.En revanche, utiliser trop de couches peut entraîner un lissage excessif et des informations peuvent être perdues dans des goulots d'étranglement structurels du graphique.
Les complexes d'unités peuvent atténuer ces problèmes car la structure de voisinage plus riche induite par les unités de grande dimension crée des raccourcis entre des nœuds qui peuvent être éloignés. Par conséquent, les informations doivent uniquement contenir certaines étapes de calcul pour être diffusées pour être valides.
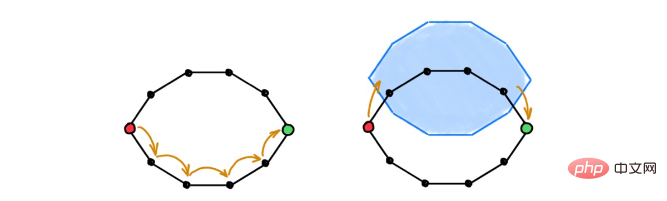 Légende : GNN nécessite de nombreuses couches pour permettre aux nœuds éloignés de communiquer (à gauche). Les cellules de grande dimension modifient la topologie sous-jacente de l'espace en créant des raccourcis (à droite). Cela permet aux nœuds distants d'échanger des informations en plusieurs étapes de messagerie.
Légende : GNN nécessite de nombreuses couches pour permettre aux nœuds éloignés de communiquer (à gauche). Les cellules de grande dimension modifient la topologie sous-jacente de l'espace en créant des raccourcis (à droite). Cela permet aux nœuds distants d'échanger des informations en plusieurs étapes de messagerie.
Modélisation hiérarchique
TopologieInformation
Les calculs effectués par transmission d'informations sont hiérarchiques et les informations circulent des unités de basse dimension vers les unités de haute dimension et inversement, ce qui peut être considéré comme un système « vertical » (et différentiable). ) pool Une forme de pooling « horizontal » dans les réseaux de neurones graphiques standard. Cela préserve le biais inductif des régions de graphique « compressées » sans ignorer les informations fines du graphique d'entrée qui nuiraient aux performances basées sur le pooling GNN.
Légende : Le transfert d'informations topologiques permet aux informations d'exister en couches entre des unités de différentes dimensions
Alignement de domaine
Certaines applications sont naturellement cohérentes avec la structure des complexes cellulaires, par exemple, les atomes, les liaisons et les anneaux chimiques peuvent être représenté par 0 cellule, 1 cellule et 2 cellules. La correspondance directe entre la structure physique de la molécule et la représentation complexe de la cellule permet au transfert d'informations topologiques de tirer parti des propriétés ci-dessus. Le transfert d'informations permet d'obtenir des résultats de pointe dans les tâches de prédiction des propriétés moléculaires.
D'autres applications qui présentent un bon alignement peuvent inclure des variétés discrètes (grilles) dans les applications d'infographie, les réseaux sociaux (les cliques sont particulièrement importantes) ou des graphiques spatiaux tels que Google Maps (les pâtés de maisons entre les rues peuvent être naturellement le sol est représenté comme une cellule "cube").
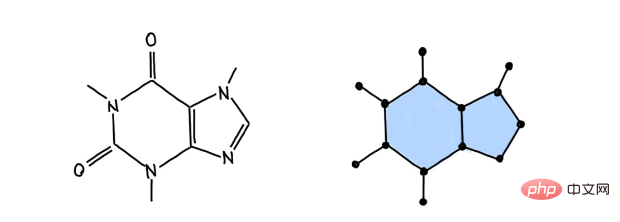
Légende : Le facteur café est modélisé comme un complexe cellulaire bidimensionnel
2 La combinaison de la topologie et de la géométrie différentielle
Algèbre de trous et équivalence de direction
En topologie algébrique, il est courant d'utiliser des complexes simpliciaux dirigés, où il y a une "orientation" arbitraire pour chaque simplexe, par exemple, on choisit un nœud source et un nœud cible, et choisissez un ordre de parcours de ses nœuds pour chaque triangle. Une fois la direction choisie, des opérateurs algébriques intéressants peuvent être effectués sur des formes complexes, comme le calcul des frontières de certains simplexes via des « opérateurs de frontière ». Ces opérations algébriques peuvent également être utilisées pour trouver des « trous » dans des complexes simpliciaux – des régions qui n’ont pas de frontières mais qui ne sont pas aux frontières de quelque chose d’autre. En coulisses, l’homologie persistante s’appuie sur ces calculs pour détecter les caractéristiques topologiques.
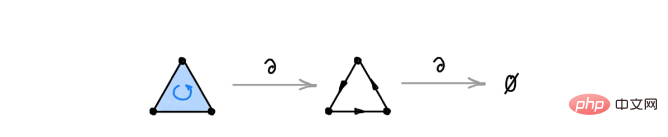
Légende : L'opérateur frontière appliqué à un 2-simplex produit un triangle. En appliquant à nouveau l’opérateur au triangle, le résultat est nul, puisque le triangle est un cycle, il n’a pas de limites.
Le transfert d'informations topologiques peut être vu comme une généralisation (non linéaire) d'opérateurs algébriques (tels que les opérateurs de frontière). Par conséquent, il est nécessaire que le transfert d’informations topologiques se comporte de manière similaire : nous voulons que la sortie de chaque couche réponde « uniformément » aux changements d’orientation du complexe d’entrée. En d’autres termes, nous voulons que nos couches soient directionnellement équivalentes. Dans notre travail, nous étudions comment le transfert d'information topologique satisfait cette propriété en choisissant des non-linéarités et des fonctions de transfert d'information appropriées, et cela est également étudié dans un cadre purement convolutif.Distinguer les espaces topologiquesL'un des premiers invariants topologiques connus, la signature d'Euler, a été à l'origine utilisée dans la classification des solides platoniciens, que nous pouvons définir comme la somme alternée du nombre de cellules dans chaque dimension. Étonnamment, si deux complexes cellulaires sont homéomorphes, ces sommes seront cohérentes même s’il s’agit de discrétisations différentes du même espace.
Fait intéressant, l'opération de lecture du modèle de transfert d'informations topologiques facilite le calcul de l'invariance de la topologie car elle applique une réduction invariante inclusive à chaque unité dimensionnelle.Par conséquent, ce type de modèle peut distinguer structurellement certains espaces non isomorphes (c'est-à-dire avoir des caractéristiques d'Euler différentes). D'un point de vue informatique, cela peut être considéré comme une généralisation du test WL, dans lequel nous cherchons non seulement à déterminer si deux complexes cellulaires sont identiques, mais également s'ils sont isomorphes l'un par rapport à l'autre.
La théorie de Hodge discrèteLa théorie de Hodge discrète fournit une explication plus géométrique des propriétés topologiques des complexes cellulaires. Lorsque le signe des caractéristiques associées à une k-cellule dépend de l'orientation de la k-cellule, ces caractéristiques peuvent être considérées mathématiquement comme des versions discrètes de formes k différentielles en géométrie différentielle (c'est-à-dire des éléments de volume à k dimensions qui peuvent être intégré) . Un opérateur appelé Hoch Laplacien généralise le Laplacien graphique et opère sur ces formes différentielles. On peut prouver que l'EDP de diffusion basée sur cet opérateur laplacien convergera dans la limite vers le signal lié au trou du composite.
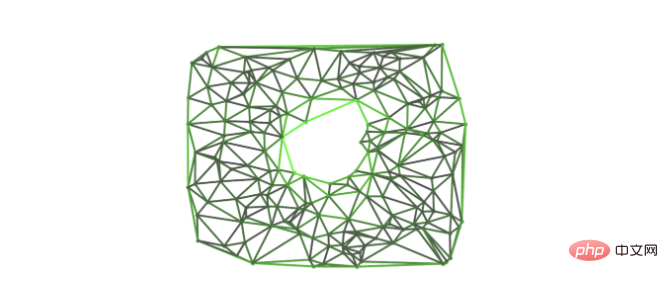
Légende : L'équation différentielle partielle de diffusion basée sur l'opérateur de Hoch Laplace converge vers la limite de la projection de la forme différentielle initiale sur le noyau de l'opérateur de Laplace. Cette image montre comment le vecteur propre nul du Hoch Laplacien prend des valeurs élevées autour des trous du complexe.
Le premier modèle simple de réseau neuronal était en fait basé sur le modèle convolutif de Hoch Laplace, lui-même inspiré du traitement topologique du signal. Tout récemment, une version du modèle convolutif basée sur cet opérateur a été utilisée pour résoudre des problèmes NP-difficiles en topologie algébrique computationnelle.3 réflexions finales
S'agit-il simplement de graphiques déguisés ?
Des articles récents soutiennent que, entre autres choses, les méthodes de transfert d'informations topologiques ne sont rien de plus que des GNN qui opèrent le transfert d'informations sur des graphiques modifiés codant pour la structure de complexes cellulaires. Cela est vrai pour les modèles convolutifs, où les calculs de transfert d'informations impliquent des paires de cellules.Cependant, dans sa forme la plus générale, la fonction
information information permet à une cellule de haute dimension de moduler les informations information transmises entre des cellules de dimension inférieure sur sa frontière. En général, les informations peuvent être transférées via des messages réguliers sur le graphique, car une arête connecte exactement deux nœuds, et une cellule à 2 peut connecter n'importe quel nombre d'arêtes. Dans les deux cas, le calcul est piloté par la topologie de l'espace sous-jacent auquel les données sont attachées. Nous pensons que les avantages de l’adoption de cette perspective topologique sur le transfert d’informations s’étendent au-delà des considérations purement informatiques. En plus de liens mathématiques précieux, il ouvre le discours de recherche à d’autres disciplines mathématiques et informatiques, facilitant ainsi une fertilisation croisée positive au sein de nos communautés souvent trop monotones.
Quelle est la prochaine étape pour la transmission des informations topologiques ?
Nous prévoyons deux principales orientations futures pour les méthodes de transfert d'informations topologiques :
Premièrement, bon nombre des architectures développées dans les GNN au fil des ans (telles que les mécanismes d'attention) pourraient être adoptées dans ces nouveaux espaces topologiques, tout en exploitant leurs caractéristiques spécifiques.
Deuxièmement, davantage d'objets et d'outils mathématiques issus du domaine de la topologie algébrique (y compris des structures comme les poulies en nid d'abeille, qui peuvent sembler étrangères même aux chercheurs en ML les plus avertis en mathématiques) seront adoptés par la communauté d'apprentissage profond des graphes et de la géométrie. .
Ces méthodes peuvent non seulement fournir des réponses à d'anciens problèmes, mais également aider à résoudre de nouveaux problèmes. Comme le disait Robert Ghrist : « les nouveaux défis nécessitent de nouvelles mathématiques » (les nouveaux défis nécessitent de nouvelles mathématiques).
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle générale (GEMM) est un élément essentiel de nombreuses applications et algorithmes, et constitue également l'un des indicateurs importants pour évaluer les performances du matériel informatique. Une recherche approfondie et l'optimisation de la mise en œuvre de GEMM peuvent nous aider à mieux comprendre le calcul haute performance et la relation entre les systèmes logiciels et matériels. En informatique, une optimisation efficace de GEMM peut augmenter la vitesse de calcul et économiser des ressources, ce qui est crucial pour améliorer les performances globales d’un système informatique. Une compréhension approfondie du principe de fonctionnement et de la méthode d'optimisation de GEMM nous aidera à mieux utiliser le potentiel du matériel informatique moderne et à fournir des solutions plus efficaces pour diverses tâches informatiques complexes. En optimisant les performances de GEMM
 Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
WORD est un traitement de texte puissant. Nous pouvons utiliser Word pour éditer divers textes. Dans les tableaux Excel, nous maîtrisons les méthodes de calcul d'addition, de soustraction et de multiplicateurs. Ainsi, si nous avons besoin de calculer l'addition de valeurs numériques dans les tableaux Word, Comment soustraire le multiplicateur ? Puis-je utiliser uniquement une calculatrice pour le calculer ? La réponse est bien sûr non, WORD peut aussi le faire. Aujourd'hui, je vais vous apprendre à utiliser des formules pour calculer des opérations de base telles que l'addition, la soustraction, la multiplication et la division dans des tableaux dans des documents Word. Apprenons ensemble. Alors, aujourd'hui, permettez-moi de vous montrer en détail comment calculer l'addition, la soustraction, la multiplication et la division dans un document WORD ? Étape 1 : ouvrez un WORD, cliquez sur [Tableau] sous [Insérer] dans la barre d'outils et insérez un tableau dans le menu déroulant.
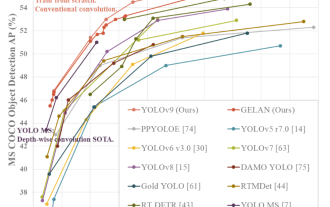 YOLO est immortel ! YOLOv9 est sorti : performances et vitesse SOTA~
Feb 26, 2024 am 11:31 AM
YOLO est immortel ! YOLOv9 est sorti : performances et vitesse SOTA~
Feb 26, 2024 am 11:31 AM
Les méthodes d'apprentissage profond d'aujourd'hui se concentrent sur la conception de la fonction objectif la plus appropriée afin que les résultats de prédiction du modèle soient les plus proches de la situation réelle. Dans le même temps, une architecture adaptée doit être conçue pour obtenir suffisamment d’informations pour la prédiction. Les méthodes existantes ignorent le fait que lorsque les données d’entrée subissent une extraction de caractéristiques couche par couche et une transformation spatiale, une grande quantité d’informations sera perdue. Cet article abordera des problèmes importants lors de la transmission de données via des réseaux profonds, à savoir les goulots d'étranglement de l'information et les fonctions réversibles. Sur cette base, le concept d'information de gradient programmable (PGI) est proposé pour faire face aux différents changements requis par les réseaux profonds pour atteindre des objectifs multiples. PGI peut fournir des informations d'entrée complètes pour la tâche cible afin de calculer la fonction objectif, obtenant ainsi des informations de gradient fiables pour mettre à jour les pondérations du réseau. De plus, un nouveau cadre de réseau léger est conçu
 Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment utiliser la fonction count() de Python pour compter le nombre d'éléments dans une liste nécessite des exemples de code spécifiques. En tant que langage de programmation puissant et facile à apprendre, Python fournit de nombreuses fonctions intégrées pour gérer différentes structures de données. L'une d'elles est la fonction count(), qui peut être utilisée pour compter le nombre d'éléments dans une liste. Dans cet article, nous expliquerons en détail comment utiliser la fonction count() et fournirons des exemples de code spécifiques. La fonction count() est une fonction intégrée de Python, utilisée pour calculer un certain
 Compter le nombre d'occurrences d'une sous-chaîne de manière récursive en Java
Sep 17, 2023 pm 07:49 PM
Compter le nombre d'occurrences d'une sous-chaîne de manière récursive en Java
Sep 17, 2023 pm 07:49 PM
Étant donné deux chaînes str_1 et str_2. Le but est de compter le nombre d'occurrences de la sous-chaîne str2 dans la chaîne str1 en utilisant une procédure récursive. Une fonction récursive est une fonction qui s'appelle dans sa définition. Si str1 est "Je sais que vous savez que je sais" et str2 est "savoir", le nombre d'occurrences est de -3 Comprenons à travers des exemples. Par exemple, entrez str1="TPisTPareTPamTP", str2="TP" ; sortie Countofoccurrencesofasubstringrecursi.
 Comment utiliser la fonction Math.Pow en C# pour calculer la puissance d'un nombre spécifié
Nov 18, 2023 am 11:32 AM
Comment utiliser la fonction Math.Pow en C# pour calculer la puissance d'un nombre spécifié
Nov 18, 2023 am 11:32 AM
En C#, il existe une bibliothèque de classes Math, qui contient de nombreuses fonctions mathématiques. Il s'agit notamment de la fonction Math.Pow, qui calcule les puissances, ce qui peut nous aider à calculer la puissance d'un nombre spécifié. L'utilisation de la fonction Math.Pow est très simple, il suffit de spécifier la base et l'exposant. La syntaxe est la suivante : Math.Pow(base,exponent) ; où base représente la base et exponent représente l'exposant. Cette fonction renvoie un résultat de type double, c'est-à-dire le résultat du calcul de puissance. Allons
 1,3 ms prend 1,3 ms ! La dernière architecture de réseau neuronal mobile open source de Tsinghua, RepViT
Mar 11, 2024 pm 12:07 PM
1,3 ms prend 1,3 ms ! La dernière architecture de réseau neuronal mobile open source de Tsinghua, RepViT
Mar 11, 2024 pm 12:07 PM
Adresse papier : https://arxiv.org/abs/2307.09283 Adresse code : https://github.com/THU-MIG/RepViTRepViT fonctionne bien dans l'architecture ViT mobile et présente des avantages significatifs. Ensuite, nous explorons les contributions de cette étude. Il est mentionné dans l'article que les ViT légers fonctionnent généralement mieux que les CNN légers sur les tâches visuelles, principalement en raison de leur module d'auto-attention multi-têtes (MSHA) qui permet au modèle d'apprendre des représentations globales. Cependant, les différences architecturales entre les ViT légers et les CNN légers n'ont pas été entièrement étudiées. Dans cette étude, les auteurs ont intégré des ViT légers dans le système efficace.
 Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Introduction Le programme Java pour calculer l'aire d'un triangle à l'aide d'un déterminant est un programme concis et efficace qui peut calculer l'aire d'un triangle à partir des coordonnées de trois sommets. Ce programme est utile à toute personne qui apprend ou travaille avec la géométrie, car il montre comment utiliser les calculs arithmétiques et algébriques de base en Java, ainsi que comment utiliser la classe Scanner pour lire les entrées de l'utilisateur. Le programme demande à l'utilisateur les coordonnées de trois points du triangle, qui sont ensuite lues et utilisées pour calculer le déterminant de la matrice de coordonnées. Utilisez la valeur absolue du déterminant pour vous assurer que l'aire est toujours positive, puis utilisez une formule pour calculer l'aire du triangle et l'afficher à l'utilisateur. Le programme peut être facilement modifié pour accepter des entrées dans différents formats ou pour effectuer des calculs supplémentaires, ce qui en fait un outil polyvalent pour les calculs géométriques. rangs de déterminants





