 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Comment prouver qu'un problème est un problème VPN ? Les informaticiens ont trouvé un moyen simple
Comment prouver qu'un problème est un problème VPN ? Les informaticiens ont trouvé un moyen simple
Comment prouver qu'un problème est un problème VPN ? Les informaticiens ont trouvé un moyen simple
Le problème P/NP est un problème non résolu dans le domaine de la complexité informatique. Les gens ont essayé de trouver la réponse à une question : « Pouvons-nous résoudre efficacement tous les problèmes informatiques dans un délai raisonnable ? »
Qu'est-ce qu'un délai raisonnable ? En fait, les problèmes qui peuvent être résolus avant la fin de l’univers sont envisagés dans un délai raisonnable. Pourtant, de nombreux problèmes semblent difficiles à résoudre dans un délai raisonnable, ce qui oblige les mathématiques à démontrer la difficulté de ces problèmes.
Une étude de 2021 répond à la question ci-dessus, ce qui confirme : Une grande partie des problèmes sont difficiles à résoudre efficacement.
Paul Beame de l'Université de Washington a commenté cette recherche : "Comme gravir une montagne, cette recherche est un point d'arrêt sur le chemin de la recherche en théorie computationnelle."

Les trois chercheurs de la recherche : des informaticiens Srikanth Srinivasan (à gauche), Nutan Limaye (en haut à droite) et Sébastien Tavenas.
L'étude a examiné des problèmes impliquant uniquement l'addition et la multiplication, mais ils deviennent très difficiles lorsque ces problèmes se limitent à être résolus d'une manière spécifique (un certain modèle alterné d'addition et de multiplication).
Étonnamment, l'étude n'a pas utilisé de nouveau cadre ou outil, les auteurs ont réussi à contourner des décennies de travail décrit par Wigderson, professeur à l'École de mathématiques de l'Institute for Advanced Study de Princeton, en collaboration avec Noam Nisan. à l'Université hébraïque de Jérusalem.
L'un des chercheurs, Srikanth Srinivasan de l'Université d'Aarhus au Danemark, a déclaré : « Nous avons réalisé qu'il existe un moyen très simple de contourner cet obstacle. Et si une méthode aussi simple pouvait être utilisée pour faire ce que nous pensions impossible , alors il doit y avoir une meilleure solution. "
Question importante
Après l'avènement des ordinateurs, les scientifiques ont découvert que les algorithmes informatiques peuvent résoudre de nombreux problèmes, mais parfois ces algorithmes prennent trop de temps - plus longtemps que le temps de calcul réel. .
Ils commencent à soupçonner que certains problèmes sont intrinsèquement trop difficiles à résoudre, quelle que soit leur taille. Par exemple, dans les graphiques, un problème important consiste à déterminer s’il existe un chemin hamiltonien, c’est-à-dire s’il existe un chemin passant par chaque sommet exactement une fois. L'augmentation du nombre de sommets (et d'arêtes) devrait prendre plus de temps pour déterminer si un tel chemin existe, mais même les meilleurs algorithmes prennent un temps exponentiellement plus long à mesure que la taille du graphique augmente, ce qui rend la résolution de ce problème irréaliste.
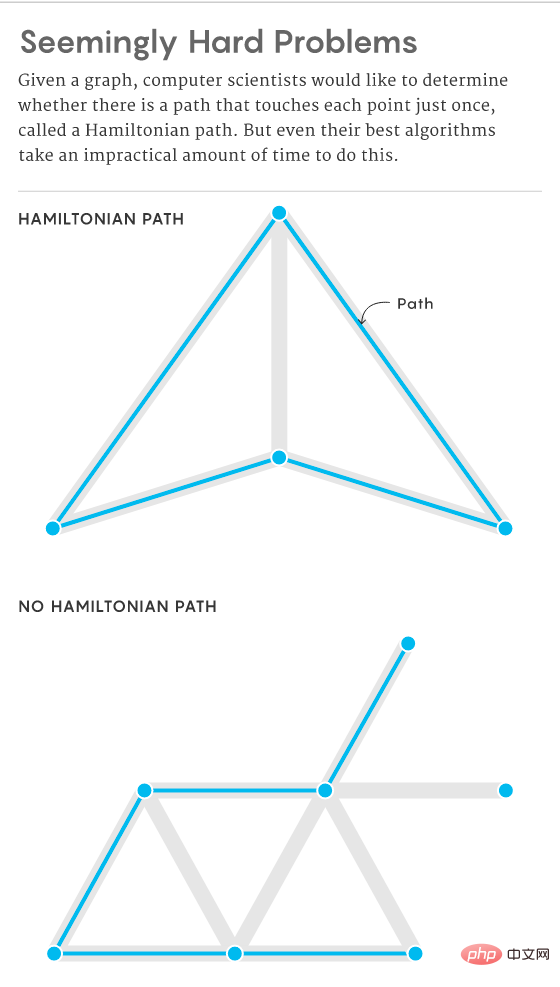
Les informaticiens tentent de prouver que tout algorithme capable de résoudre efficacement un problème difficile d'un certain type de problème d'une manière ou d'une autre peut être transformé en une solution à d'autres problèmes tout aussi difficiles. Ils appellent ce type de problème problème NP.
Bien sûr, il existe aussi de nombreux problèmes qui ne semblent pas difficiles et ne prennent pas trop de temps à résoudre. Beaucoup de ces problèmes sont également équivalents dans un certain sens, et ces problèmes sont appelés problèmes P. Ils soutiennent que les problèmes NP sont en effet plus difficiles que les problèmes P et que les problèmes NP ne peuvent jamais être résolus efficacement. Mais sans preuves, cette idée pourrait être fausse.
Les informaticiens ont donc commencé à chercher des moyens de prouver que les problèmes NP sont effectivement plus difficiles. Cela nécessitait de prouver que les problèmes NP doivent prendre un temps exponentiel à résoudre, mais prouver que cela n'est pas facile.
À quel point est-ce que « dur » est difficile ?
Imaginez un ensemble spécifique de problèmes qui ne nécessitent que des additions et des multiplications. Par exemple, étant donné un ensemble de points, il est possible de calculer tous les chemins hamiltoniens possibles (s'ils existent) en utilisant les données sur les points, simplement par addition et multiplication.
À mesure que la taille du problème augmente, certains problèmes arithmétiques (tels que le calcul des chemins hamiltoniens) prennent plus de temps. En 1979, Leslie Valiant de l'Université Harvard a montré que de nombreux problèmes arithmétiques sont équivalents en termes de difficulté, tandis que d'autres sont équivalents en termes d'absence de difficulté. Les informaticiens ont ensuite donné son nom à ces deux types de problèmes, respectivement VNP et VP.
Et P Comme le problème NP, nous ne pouvons pas prouver la difficulté du problème VNP. Nous savons seulement que le problème VNP est plus difficile que le problème NP car il est basé sur ce dernier. Par exemple, calculer un chemin nécessite d'abord de déterminer si. le chemin existe.
« C’est plus difficile que NP, donc il devrait être plus facile de montrer que c’est difficile », a déclaré Shpilka.
Au cours des décennies suivantes, les informaticiens ont fait des progrès beaucoup plus importants sur le problème VP contre VNP que sur le problème P contre NP, mais la plupart se limitaient à ce que Valiant a créé, appelé sous-champs de complexité algébrique. Avant les travaux récents de Limaye, Srinivasan et Tavenas, il était encore difficile de dire s'il y avait des problèmes en arithmétique au sens général.
Ajustement des polynômes
Ce nouveau travail permet d'explorer la façon dont les informaticiens réfléchissent aux problèmes d'addition et de multiplication. Mathématiquement, ces problèmes peuvent être écrits en termes de polynômes (par exemple x^2 + 5y + 6) constitués de variables ajoutées et multipliées.
Pour tout problème particulier, comme le calcul d'un chemin hamiltonien, vous pouvez construire un polynôme qui le représente. Par exemple, vous pouvez utiliser une variable pour représenter chaque point et chaque arête, de sorte qu'à mesure que davantage de points et d'arêtes sont ajoutés, davantage de variables puissent être ajoutées au polynôme.
Pour montrer qu'un problème arithmétique comme le calcul d'un chemin hamiltonien est difficile, il faut montrer que plus on ajoute de points et d'arêtes, plus les polynômes correspondants nécessitent plus d'opérations pour être résolus en temps exponentiel. Par exemple, x^2 nécessite une opération (x * x), tandis que x^2 + y nécessite deux opérations (x * x plus y). Le nombre d'opérations est appelé taille du polynôme.
Mais la taille du polynôme est difficile à déterminer. Par exemple le polynôme x^2 + 2x + 1. Il semble avoir une taille de 4 (deux multiplications et deux additions), mais le polynôme peut être réécrit comme le produit de deux sommes, (x + 1)(x + 1), qui a moins d'opérandes - deux fois l'addition, une multiplication. Souvent, à mesure qu’un problème s’agrandit et que davantage de variables sont ajoutées au polynôme, les transformations mathématiques peuvent aider à simplifier et à réduire sa taille.
Quelques années après les recherches de Valiant, des informaticiens ont trouvé un moyen de faciliter l’analyse de l’ampleur du problème. Pour ce faire, ils ont proposé une propriété appelée « profondeur », qui spécifie le nombre de fois où le polynôme bascule ou alterne entre sommes et produits. Par exemple, le polynôme x^2 + 2x + 1 a une profondeur de 2 car il s'agit de la somme de produits (tels que x^2 et 2x). En revanche, l'expression (x + 1)(x + 1) a une profondeur de 3 car elle a la même profondeur que 0 + (x + 1)(x + 1), calculée comme la somme des produits.
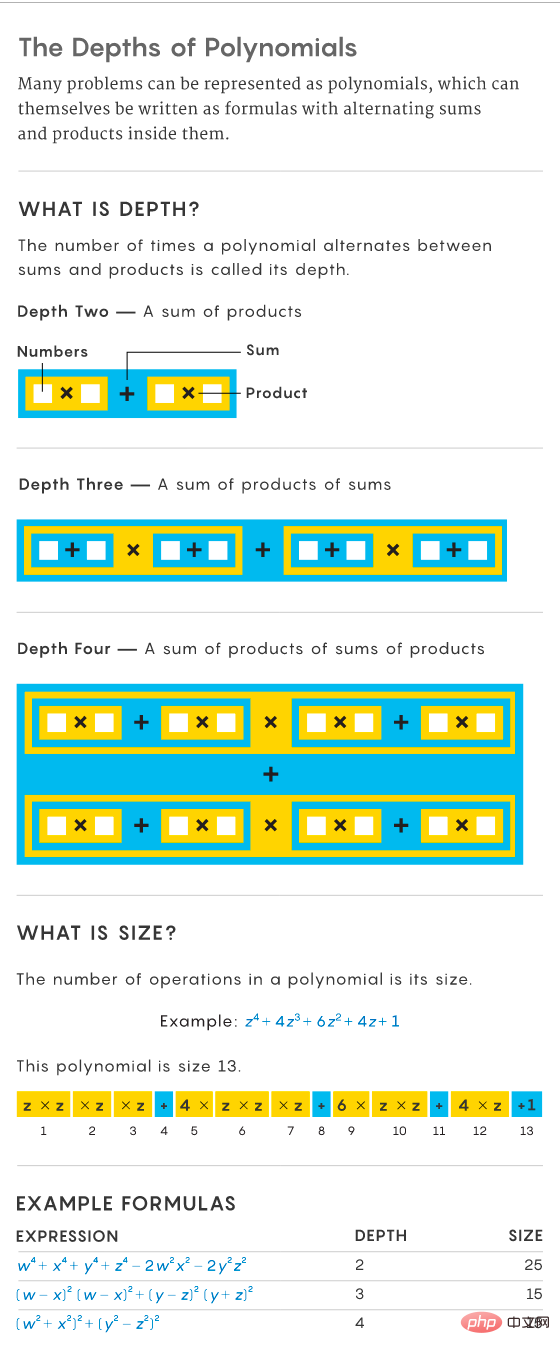
Pour simplifier les polynômes, les informaticiens les contraignent à une forme fixe avec une propriété appelée « profondeur constante », où le modèle des sommes et des produits ne change pas à mesure que le problème grandit. Cela les rend de taille plus fixe, la taille du polynôme diminuant à mesure que sa profondeur augmente. Une expression pour une profondeur constante s’appelle une formule. Une profondeur constante permet de progresser davantage dans l'étude des polynômes.
"Profondeur" magique
En 1996, un article de Nisan et Wigderson s'est concentré sur la résolution du problème de la multiplication matricielle. Ils ont simplifié ce problème de deux manières. Tout d’abord, ils l’ont exprimé en utilisant la formule de profondeur constante – une profondeur de 3. Deuxièmement, ils n’ont considéré que des formules ayant une structure simple dans lesquelles chaque variable a un exposant maximum de 1, ce qui fait du problème initial un problème « multilinéaire ».
Les informaticiens ont découvert que certains problèmes peuvent être convertis en structures ensemble-multilinéaires relativement simples au détriment d'une augmentation sous-exponentielle de la taille du polynôme (comparable au taux de croissance de la croissance exponentielle).
Nisan et Wigderson ont montré plus tard que le problème de multiplication matricielle prend un temps exponentiel à résoudre à mesure que la matrice grandit. En d’autres termes, ils montrent qu’un problème important est difficile, et ils s’efforcent de montrer qu’une catégorie de problèmes est difficile. Cependant, leurs résultats ne sont valables que pour des formulations avec des structures multilinéaires simples et collectives.

Leslie Valiant
Augmenter la profondeur d'un polynôme a tendance à faire diminuer sa taille. Au fil du temps, les informaticiens ont précisé l’arbitrage entre ces deux propriétés. Ils montrent qu’en ajoutant deux niveaux de profondeur à la profondeur 3, les polynômes multilinéaires d’ensemble peuvent équilibrer le gain de taille de leur structure multilinéaire d’ensemble. Si les formules structurées de profondeur 5 prennent un temps exponentiel, il en va de même pour les formules de profondeur 3 de nature générale et non structurée.
De nouveaux travaux de Srikanth Srinivasan et al. montrent que les formulations multilinéaires profondes en 5 ensembles de problèmes de multiplication matricielle croissent effectivement à un rythme exponentiel. Cela signifie que la formule générale de profondeur 3 prend également un temps exponentiel. Ils ont ensuite montré qu’une tendance similaire était valable pour toutes les profondeurs (pas seulement 3 et 5). Avec cette relation, ils ont montré que la taille d’une formule générale de toute profondeur pour le même problème croît de façon exponentielle avec la taille du problème.
Ils montrent également qu'il est difficile d'exprimer la multiplication matricielle dans une formule à profondeur constante, quelle que soit cette profondeur.
Les résultats de cette étude fournissent la première compréhension générale du moment où un problème arithmétique est « difficile » - lorsqu'il ne peut pas être exprimé dans une formule à profondeur constante. Le problème spécifique de la multiplication matricielle est connu sous le nom de problème VP. Et on sait que le problème VP est relativement simple lorsqu'il n'est pas limité à une profondeur constante, il s'avère donc que la profondeur constante est la source de la « difficulté » du problème.
Les problèmes VNP sont-ils plus difficiles que les problèmes VP ? Les nouveaux résultats n’illustrent pas directement cela, ils montrent seulement que la formule de profondeur constante est difficile. Mais cela reste une étape importante pour prouver que le problème VNP ne peut pas être équivalent au problème VP.
Pour le problème plus vaste P vs NP, nous pouvons désormais être plus optimistes que la réponse sera un jour trouvée. Après tout, pour résoudre des problèmes difficiles, nous devons d’abord savoir quelles directions sont désespérées.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1393
1393
 52
52
 1206
1206
 24
24
 La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle générale (GEMM) est un élément essentiel de nombreuses applications et algorithmes, et constitue également l'un des indicateurs importants pour évaluer les performances du matériel informatique. Une recherche approfondie et l'optimisation de la mise en œuvre de GEMM peuvent nous aider à mieux comprendre le calcul haute performance et la relation entre les systèmes logiciels et matériels. En informatique, une optimisation efficace de GEMM peut augmenter la vitesse de calcul et économiser des ressources, ce qui est crucial pour améliorer les performances globales d’un système informatique. Une compréhension approfondie du principe de fonctionnement et de la méthode d'optimisation de GEMM nous aidera à mieux utiliser le potentiel du matériel informatique moderne et à fournir des solutions plus efficaces pour diverses tâches informatiques complexes. En optimisant les performances de GEMM
 Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
WORD est un traitement de texte puissant. Nous pouvons utiliser Word pour éditer divers textes. Dans les tableaux Excel, nous maîtrisons les méthodes de calcul d'addition, de soustraction et de multiplicateurs. Ainsi, si nous avons besoin de calculer l'addition de valeurs numériques dans les tableaux Word, Comment soustraire le multiplicateur ? Puis-je utiliser uniquement une calculatrice pour le calculer ? La réponse est bien sûr non, WORD peut aussi le faire. Aujourd'hui, je vais vous apprendre à utiliser des formules pour calculer des opérations de base telles que l'addition, la soustraction, la multiplication et la division dans des tableaux dans des documents Word. Apprenons ensemble. Alors, aujourd'hui, permettez-moi de vous montrer en détail comment calculer l'addition, la soustraction, la multiplication et la division dans un document WORD ? Étape 1 : ouvrez un WORD, cliquez sur [Tableau] sous [Insérer] dans la barre d'outils et insérez un tableau dans le menu déroulant.
 Une plongée approfondie dans les modèles, les données et les frameworks : une revue exhaustive de 54 pages de grands modèles de langage efficaces
Jan 14, 2024 pm 07:48 PM
Une plongée approfondie dans les modèles, les données et les frameworks : une revue exhaustive de 54 pages de grands modèles de langage efficaces
Jan 14, 2024 pm 07:48 PM
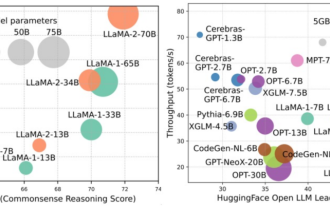
Les modèles linguistiques à grande échelle (LLM) ont démontré des capacités convaincantes dans de nombreuses tâches importantes, notamment la compréhension du langage naturel, la génération de langages et le raisonnement complexe, et ont eu un impact profond sur la société. Cependant, ces capacités exceptionnelles nécessitent des ressources de formation importantes (illustrées dans l’image de gauche) et de longs temps d’inférence (illustrés dans l’image de droite). Les chercheurs doivent donc développer des moyens techniques efficaces pour résoudre leurs problèmes d’efficacité. De plus, comme on peut le voir sur le côté droit de la figure, certains LLM (LanguageModels) efficaces tels que Mistral-7B ont été utilisés avec succès dans la conception et le déploiement de LLM. Ces LLM efficaces peuvent réduire considérablement la mémoire d'inférence tout en conservant une précision similaire à celle du LLaMA1-33B
 Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment utiliser la fonction count() de Python pour compter le nombre d'éléments dans une liste nécessite des exemples de code spécifiques. En tant que langage de programmation puissant et facile à apprendre, Python fournit de nombreuses fonctions intégrées pour gérer différentes structures de données. L'une d'elles est la fonction count(), qui peut être utilisée pour compter le nombre d'éléments dans une liste. Dans cet article, nous expliquerons en détail comment utiliser la fonction count() et fournirons des exemples de code spécifiques. La fonction count() est une fonction intégrée de Python, utilisée pour calculer un certain
 Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Introduction Le programme Java pour calculer l'aire d'un triangle à l'aide d'un déterminant est un programme concis et efficace qui peut calculer l'aire d'un triangle à partir des coordonnées de trois sommets. Ce programme est utile à toute personne qui apprend ou travaille avec la géométrie, car il montre comment utiliser les calculs arithmétiques et algébriques de base en Java, ainsi que comment utiliser la classe Scanner pour lire les entrées de l'utilisateur. Le programme demande à l'utilisateur les coordonnées de trois points du triangle, qui sont ensuite lues et utilisées pour calculer le déterminant de la matrice de coordonnées. Utilisez la valeur absolue du déterminant pour vous assurer que l'aire est toujours positive, puis utilisez une formule pour calculer l'aire du triangle et l'afficher à l'utilisateur. Le programme peut être facilement modifié pour accepter des entrées dans différents formats ou pour effectuer des calculs supplémentaires, ce qui en fait un outil polyvalent pour les calculs géométriques. rangs de déterminants
 Crushing H100, le GPU nouvelle génération de Nvidia se dévoile ! La première conception de module multipuce 3 nm, dévoilée en 2024
Sep 30, 2023 pm 12:49 PM
Crushing H100, le GPU nouvelle génération de Nvidia se dévoile ! La première conception de module multipuce 3 nm, dévoilée en 2024
Sep 30, 2023 pm 12:49 PM
Processus 3 nm, les performances dépassent le H100 ! Récemment, le média étranger DigiTimes a annoncé que Nvidia développait le GPU de nouvelle génération, le B100, dont le nom de code est "Blackwell". Il s'agirait d'un produit destiné aux applications d'intelligence artificielle (IA) et de calcul haute performance (HPC). , le B100 utilisera le processus de traitement 3 nm de TSMC, ainsi qu'une conception de module multi-puces (MCM) plus complexe, et apparaîtra au quatrième trimestre 2024. Pour Nvidia, qui monopolise plus de 80 % du marché des GPU d’intelligence artificielle, il peut utiliser le B100 pour frapper pendant que le fer est chaud et attaquer davantage des challengers comme AMD et Intel dans cette vague de déploiement d’IA. Selon les estimations de NVIDIA, d'ici 2027, la valeur de production de ce domaine devrait atteindre environ
 Compter le nombre d'occurrences d'une sous-chaîne de manière récursive en Java
Sep 17, 2023 pm 07:49 PM
Compter le nombre d'occurrences d'une sous-chaîne de manière récursive en Java
Sep 17, 2023 pm 07:49 PM
Étant donné deux chaînes str_1 et str_2. Le but est de compter le nombre d'occurrences de la sous-chaîne str2 dans la chaîne str1 en utilisant une procédure récursive. Une fonction récursive est une fonction qui s'appelle dans sa définition. Si str1 est "Je sais que vous savez que je sais" et str2 est "savoir", le nombre d'occurrences est de -3 Comprenons à travers des exemples. Par exemple, entrez str1="TPisTPareTPamTP", str2="TP" ; sortie Countofoccurrencesofasubstringrecursi.
 Comment utiliser la fonction Math.Pow en C# pour calculer la puissance d'un nombre spécifié
Nov 18, 2023 am 11:32 AM
Comment utiliser la fonction Math.Pow en C# pour calculer la puissance d'un nombre spécifié
Nov 18, 2023 am 11:32 AM
En C#, il existe une bibliothèque de classes Math, qui contient de nombreuses fonctions mathématiques. Il s'agit notamment de la fonction Math.Pow, qui calcule les puissances, ce qui peut nous aider à calculer la puissance d'un nombre spécifié. L'utilisation de la fonction Math.Pow est très simple, il suffit de spécifier la base et l'exposant. La syntaxe est la suivante : Math.Pow(base,exponent) ; où base représente la base et exponent représente l'exposant. Cette fonction renvoie un résultat de type double, c'est-à-dire le résultat du calcul de puissance. Allons



