
Le contenu d'un objet ndarray est accessible et modifié via l'indexation ou le découpage, tout comme l'opération de découpage pour les listes en Python.
Le tableau ndarray peut être indexé en fonction des indices de 0 à n-1. L'objet slice peut être découpé dans un nouveau tableau à partir du tableau d'origine via la fonction slice intégrée et en définissant les paramètres de démarrage, d'arrêt et d'étape. .
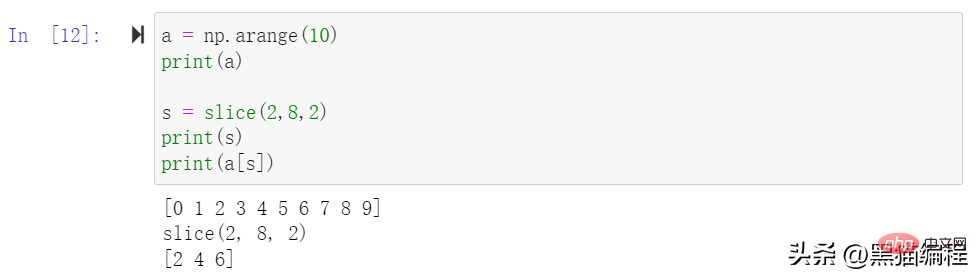

Les tranches peuvent également inclure des ellipses… pour que la longueur du tuple de sélection soit la même que les dimensions du tableau. Si des points de suspension sont utilisés à la position de la ligne, ils renverront un ndarray contenant les éléments de la ligne.
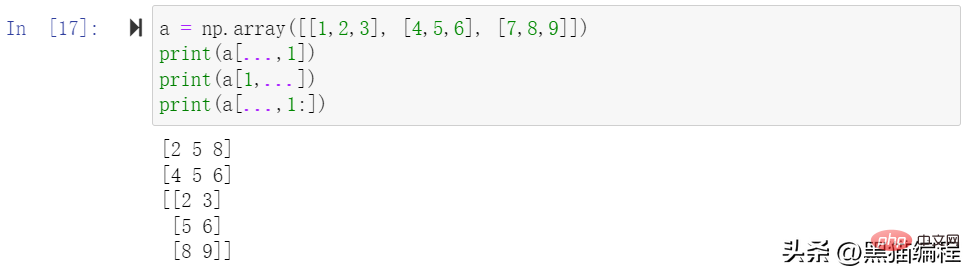
L'exemple suivant récupère les éléments aux positions (0,0), (1,1) et (2,0) dans le tableau.

a = np.array([[0,1,2], [3,4,5], [6,7,8], [9,10,11]])
print(a)
print('-' * 20)
rows = np.array([[0,0], [3,3]])
cols = np.array([[0,2], [0,2]])
b = a[rows, cols]
print(b)
print('-' * 20)
rows = np.array([[0,1], [2,3]])
cols = np.array([[0,2], [0,2]])
c = a[rows, cols]
print(c)
print('-' * 20)
rows = np.array([[0,1,2], [1,2,3], [1,2,3]])
cols = np.array([[0,1,2], [0,1,2], [0,1,2]])
d = a[rows, cols]
print(d)Le résultat renvoyé est un objet ndarray contenant chaque élément de coin.
Peut être combiné avec des tableaux indexés à l'aide de tranches : ou ... . Comme dans l'exemple suivant :
[[ 012] [ 345] [ 678] [ 9 10 11]] -------------------- [[ 02] [ 9 11]] -------------------- [[ 05] [ 6 11]] -------------------- [[ 048] [ 37 11] [ 37 11]]
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(a)
print('-' * 20)
b = a[1:3, 1:3]
print(b)
print('-' * 20)
c = a[1:3, [0,2]]
print(c)
print('-' * 20)
d = a[..., 1:]
print(d)Nous pouvons indexer le tableau cible via un tableau booléen.
L'indexation booléenne utilise des opérations booléennes (telles que des opérateurs de comparaison) pour obtenir un tableau d'éléments qui répondent à des conditions spécifiées.
L'exemple suivant obtient des éléments supérieurs à 5 :
[[1 2 3] [4 5 6] [7 8 9]] -------------------- [[5 6] [8 9]] -------------------- [[4 6] [7 9]] -------------------- [[2 3] [5 6] [8 9]]
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(a)
print('-' * 20)
print(a[a > 5])L'exemple suivant utilise ~ (opérateur complémentaire) pour filtrer NaN.
[[1 2 3] [4 5 6] [7 8 9]] -------------------- [6 7 8 9]
a = np.array([np.nan, 1, 2, np.nan, 3, 4, 5])
print(a)
print('-' * 20)
print(a[~np.isnan(a)])L'exemple suivant montre comment filtrer les éléments non complexes d'un tableau.
[nan1.2. nan3.4.5.] -------------------- [1. 2. 3. 4. 5.]
a = np.array([1, 3+4j, 5, 6+7j])
print(a)
print('-' * 20)
print(a[np.iscomplex(a)])L'indexation sophistiquée fait référence à l'utilisation d'un tableau d'entiers pour l'indexation.
Fancy index prend la valeur basée sur la valeur du tableau d'index comme indice d'un axe du tableau cible.
Pour utiliser un tableau d'entiers unidimensionnels comme index, si la cible est un tableau unidimensionnel, alors le résultat de l'index est l'élément à la position correspondante. Si la cible est un tableau à deux dimensions, alors c'est le cas. la ligne correspondant à l'indice.
L'indexation sophistiquée est différente du découpage, elle copie toujours les données dans un nouveau tableau.
Tableau unidimensionnel
[1.+0.j 3.+4.j 5.+0.j 6.+7.j] -------------------- [3.+4.j 6.+7.j]
a = np.arange(2, 10)
print(a)
print('-' * 20)
b = a[[0,6]]
print(b)Tableau bidimensionnel
1. Passer dans le tableau d'index séquentiel
[2 3 4 5 6 7 8 9] -------------------- [2 8]
a = np.arange(32).reshape(8, 4)
print(a)
print('-' * 20)
print(a[[4, 2, 1, 7]])2. -tableau d'index de commande
[[ 0123] [ 4567] [ 89 10 11] [12 13 14 15] [16 17 18 19] [20 21 22 23] [24 25 26 27] [28 29 30 31]] -------------------- [[16 17 18 19] [ 89 10 11] [ 4567] [28 29 30 31]]
3, transmettez plusieurs tableaux d'index (pour utiliser np.ix_)
np.ix_ la fonction consiste à saisir deux tableaux et à générer une relation de mappage de produit cartésien.
Le produit cartésien fait référence au produit cartésien (produit cartésien) de deux ensembles X et Y en mathématiques, également appelé produit direct, exprimé par X×Y, le premier objet est membre de Le deuxième objet est un membre de toutes les paires ordonnées possibles de Y.
Par exemple, A={a,b}, B={0,1,2}, alors :
a = np.arange(32).reshape(8, 4) print(a[[-4, -2, -1, -7]])
[[16 17 18 19] [24 25 26 27] [28 29 30 31] [ 4567]]
A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}Broadcast (Broadcast) est un tableau numpy de formes différentes ( forme) De la même manière que les calculs numériques sont effectués, les opérations arithmétiques sur les tableaux sont généralement effectuées sur les éléments correspondants.
如果两个数组 a 和 b 形状相同,即满足 a.shape == b.shape,那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同,且各维度的长度相同。
a = np.arange(1, 5) b = np.arange(1, 5) c = a * b print(c)
[ 149 16]
当运算中的 2 个数组的形状不同时,numpy 将自动触发广播机制。如:
a = np.array([ [0, 0, 0], [10, 10, 10], [20, 20, 20], [30, 30, 30] ]) b = np.array([0, 1, 2]) print(a + b)
[[ 012] [10 11 12] [20 21 22] [30 31 32]]
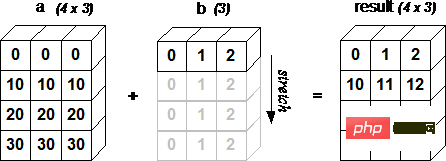
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。
tile扩展数组
a = np.array([1, 2])
b = np.tile(a, (6, 1))
print(b)
print('-' * 20)
c = np.tile(a, (2, 3))
print(c)[[1 2] [1 2] [1 2] [1 2] [1 2] [1 2]] -------------------- [[1 2 1 2 1 2] [1 2 1 2 1 2]]
4x3 的二维数组与长为 3 的一维数组相加,等效于把数组 b 在二维上重复 4 次再运算:
a = np.array([ [0, 0, 0], [10, 10, 10], [20, 20, 20], [30, 30, 30] ]) b = np.array([0, 1, 2]) bb = np.tile(b, (4, 1)) print(a + bb)
[[ 012] [10 11 12] [20 21 22] [30 31 32]]
广播的规则:
简单理解:对两个数组,分别比较他们的每一个维度(若其中一个数组没有当前维度则忽略),满足:
若条件不满足,抛出 "ValueError: frames are not aligned" 异常。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!