 Périphériques technologiques
Périphériques technologiques
 IA
IA
 La recherche opérationnelle basée sur l'IA optimise les « machines de lithographie » ! L'Université des sciences et technologies de Chine et d'autres ont proposé un modèle de séquence hiérarchique pour améliorer considérablement l'efficacité de la résolution de la programmation mathématique.
La recherche opérationnelle basée sur l'IA optimise les « machines de lithographie » ! L'Université des sciences et technologies de Chine et d'autres ont proposé un modèle de séquence hiérarchique pour améliorer considérablement l'efficacité de la résolution de la programmation mathématique.
La recherche opérationnelle basée sur l'IA optimise les « machines de lithographie » ! L'Université des sciences et technologies de Chine et d'autres ont proposé un modèle de séquence hiérarchique pour améliorer considérablement l'efficacité de la résolution de la programmation mathématique.
Les solveurs de programmation mathématique sont connus sous le nom de « machines lithographiques » dans le domaine de la recherche opérationnelle et de l'optimisation en raison de leur importance et de leur polyvalence.
Parmi eux, la programmation linéaire en nombres entiers mixtes (MILP) est un élément clé des solveurs de programmation mathématique et peut modéliser un grand nombre d'applications pratiques, telles que la planification de la production industrielle, la planification logistique, la conception de puces, la planification de chemins, l'investissement financier, etc. .des domaines majeurs.
Récemment, l'équipe du professeur Wang Jie du laboratoire MIRA de l'Université des sciences et technologies de Chine et du laboratoire Noah's Ark de Huawei ont proposé conjointement le modèle de séquence hiérarchique (HEM), qui améliore considérablement l'efficacité de résolution du solveur de programmation linéaire en nombres entiers mixtes. Les résultats pertinents ont été publiés dans ICLR 2023.
Actuellement, l'algorithme a été intégré à la bibliothèque de modèles MindSpore ModelZoo de Huawei, et les technologies et capacités associées seront intégrées au solveur OptVerse AI de Huawei au cours de cette année. Ce solveur vise à combiner la recherche opérationnelle et l'IA pour dépasser les limites d'optimisation de la recherche opérationnelle de l'industrie, aider les entreprises dans la prise de décision quantitative et les opérations raffinées, et parvenir à une réduction des coûts et à une amélioration de l'efficacité !

Liste des auteurs : Wang Zhihai*, Li Xijun*, Wang Jie**, Kuang Yufei, Yuan Mingxuan, Zeng Jia, Zhang Yongdong, Wu Feng
Lien papier : https://openreview.net/ forum?id=Zob4P9bRNcK
Ensemble de données open source : https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing
Code open source de la version PyTorch : https://github.com/MIRALab -USTC/L2O-HEM- Code open source de la version Torch
MindSpore : https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut
Tianchou (OptVerse) AI solveur : https://www.huaweicloud.com/product/modelarts/optverse.html
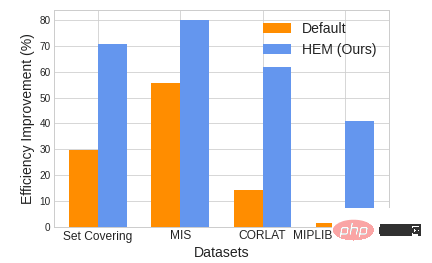
Figure 1. Comparaison de l'efficacité de résolution entre HEM et la stratégie par défaut du solveur (l'efficacité de résolution de HEM par défaut peut être améliorée par). jusqu'à 47,28%
1 Introduction
Les plans de coupe (coupes) sont cruciaux pour résoudre efficacement les problèmes de programmation linéaire en nombres entiers mixtes.
La sélection du plan de coupe (sélection de coupe) vise à sélectionner un sous-ensemble approprié de plans de coupe à sélectionner pour améliorer l'efficacité de la résolution du MILP. La sélection du plan de coupe dépend fortement de deux sous-problèmes : (P1) quels plans de coupe doivent être préférés et (P2) combien de plans de coupe doivent être sélectionnés.
Alors que de nombreux solveurs MILP modernes gèrent (P1) et (P2) avec des heuristiques conçues manuellement, les méthodes d'apprentissage automatique ont le potentiel d'apprendre des heuristiques plus efficaces.
Cependant, de nombreuses méthodes d'apprentissage existantes se concentrent sur l'apprentissage des plans de coupe à prioriser, mais ignorent l'apprentissage du nombre de plans de coupe à sélectionner. De plus, nous avons observé à partir d’un grand nombre de résultats expérimentaux qu’un autre sous-problème, à savoir (P3), quel ordre de plan de coupe doit être préféré, a également un impact significatif sur l’efficacité de la résolution du MILP.
Pour relever ces défis, nous proposons un nouveau modèle de séquence hiérarchique (HEM) et apprenons la stratégie de sélection du plan de coupe à travers un cadre d'apprentissage par renforcement.
À notre connaissance, HEM est la première méthode d'apprentissage capable de gérer (P1), (P2) et (P3) simultanément. Les expériences montrent que HEM améliore considérablement l'efficacité de la résolution du MILP par rapport aux lignes de base conçues et apprises manuellement sur des ensembles de données MILP du monde réel générés artificiellement et à grande échelle.
2 Introduction au contexte et au problème
2.1 Introduction aux plans de coupe (coupes)
La programmation linéaire en nombres entiers mixtes (MILP) est un modèle d'optimisation général qui peut être largement utilisé dans une variété de domaines d'application pratiques, tels que la gestion de la chaîne d'approvisionnement. [1], planification de la production [2], planification et expédition [3], sélection de l'emplacement de l'usine [4], problème d'emballage [5], etc.
Le MILP standard a la forme suivante :
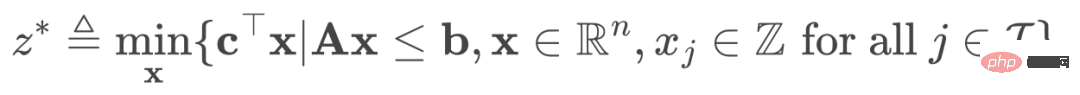
(1)
Étant donné le problème (1), nous supprimons toutes ses contraintes entières et obtenons le problème de relaxation par programmation linéaire (LPR). Sa forme est :
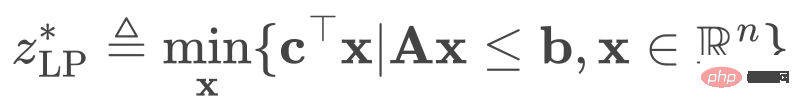
(2)
Puisque le problème (2) étend l'ensemble des réalisables du problème (1), nous pouvons avoir que la valeur optimale du problème LPR est le problème MILP d'origine Nether.
Étant donné le problème LPR dans (2), les plans de coupe (coupes) sont une classe d'inégalités linéaires légales qui, lorsqu'elles sont ajoutées au problème de relaxation de programmation linéaire, peuvent réduire l'espace de domaine réalisable dans le problème LPR, et n'en suppriment aucun solutions entières réalisables au problème MILP d’origine.
2.2 Introduction à la sélection de coupe
Le solveur MILP peut générer un grand nombre de plans de coupe pendant le processus de résolution du problème MILP, et continuera à ajouter des plans de coupe au problème d'origine au cours des tours successifs.
Plus précisément, chaque tour comprend cinq étapes :
(1) Résoudre le problème LPR actuel ;
(2) Générer une série de plans de coupe à sélectionner
(3) À partir des plans de coupe à sélectionner ; sous-ensemble approprié ;
(4) Ajoutez le sous-ensemble sélectionné au problème LPR dans (1) pour obtenir un nouveau problème LPR
(5) Répétez le cycle, en fonction du nouveau problème LPR, entrez dans le tour suivant ;
L'ajout de tous les plans de coupe générés au problème LPR réduit au maximum l'espace des régions réalisables du problème afin de maximiser la limite inférieure.
Cependant, l'ajout de trop de plans de coupe peut entraîner un problème avec trop de contraintes, augmenter la charge de calcul de la résolution du problème et provoquer une instabilité numérique [6,7].
Par conséquent, les chercheurs ont proposé la sélection du plan de coupe (sélection de coupe), qui vise à sélectionner un sous-ensemble approprié de plans de coupe candidats pour améliorer autant que possible l'efficacité de la résolution des problèmes MILP. La sélection du plan de coupe est cruciale pour améliorer l'efficacité de la résolution des problèmes de programmation linéaire en nombres entiers mixtes [8, 9, 10].
2.3 Expérience heuristique — ordre d'ajout du plan de coupe
Nous avons conçu deux algorithmes heuristiques pour la sélection du plan de coupe, à savoir RandomAll et RandomNV (voir le chapitre 3 de l'article original pour plus de détails).
Ils ajoutent tous les coupes sélectionnées au problème MILP dans un ordre aléatoire après avoir sélectionné un lot de coupes. Comme le montrent les résultats de la figure 2, lorsque le même plan de coupe est sélectionné, l'ajout de ces plans de coupe sélectionnés dans des ordres différents a un impact important sur l'efficacité de résolution du solveur (voir le chapitre 3 de l'article original pour une analyse détaillée des résultats).
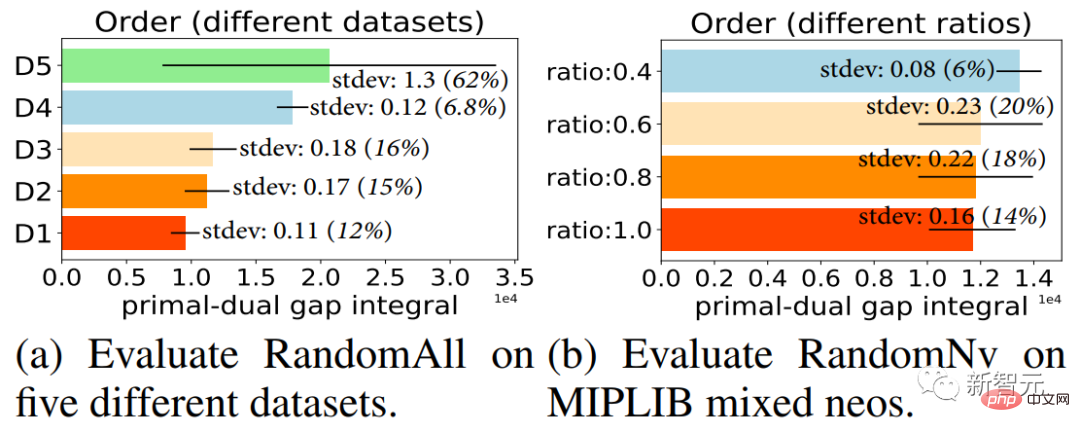
Figure 2. Chaque colonne représente la valeur moyenne de l'efficacité de la solution finale du solveur lorsque le même lot de plans de coupe est sélectionné dans le solveur et que ces plans de coupe sélectionnés sont ajoutés en 10 tours d'ordres différents. les lignes d'écart dans les colonnes représentent l'écart type de l'efficacité de la solution sous différents ordres. Plus l’écart type est grand, plus l’impact de l’ordre sur l’efficacité de résolution du solveur est grand.
3 Introduction à la méthode
Dans la tâche de sélection du plan de coupe, le sous-ensemble optimal à sélectionner ne peut pas être obtenu à l'avance.
Cependant, nous pouvons utiliser le solveur pour évaluer la qualité de tout sous-ensemble sélectionné et utiliser cette évaluation comme retour à l'algorithme d'apprentissage.
Par conséquent, nous utilisons le paradigme de l'apprentissage par renforcement (RL) pour apprendre la stratégie de sélection du plan de coupe par essais et erreurs.
Dans cette section, nous développons notre cadre RL proposé.
Tout d'abord, nous modélisons la tâche de sélection du plan de coupe comme un processus de décision de Markov (MDP) ; puis, nous présentons en détail notre modèle de séquence hiérarchique (HEM) proposé. Enfin, nous dérivons des gradients de politique hiérarchique pour une formation efficace des HEM ; Notre diagramme global de cadre RL est présenté à la figure 3.
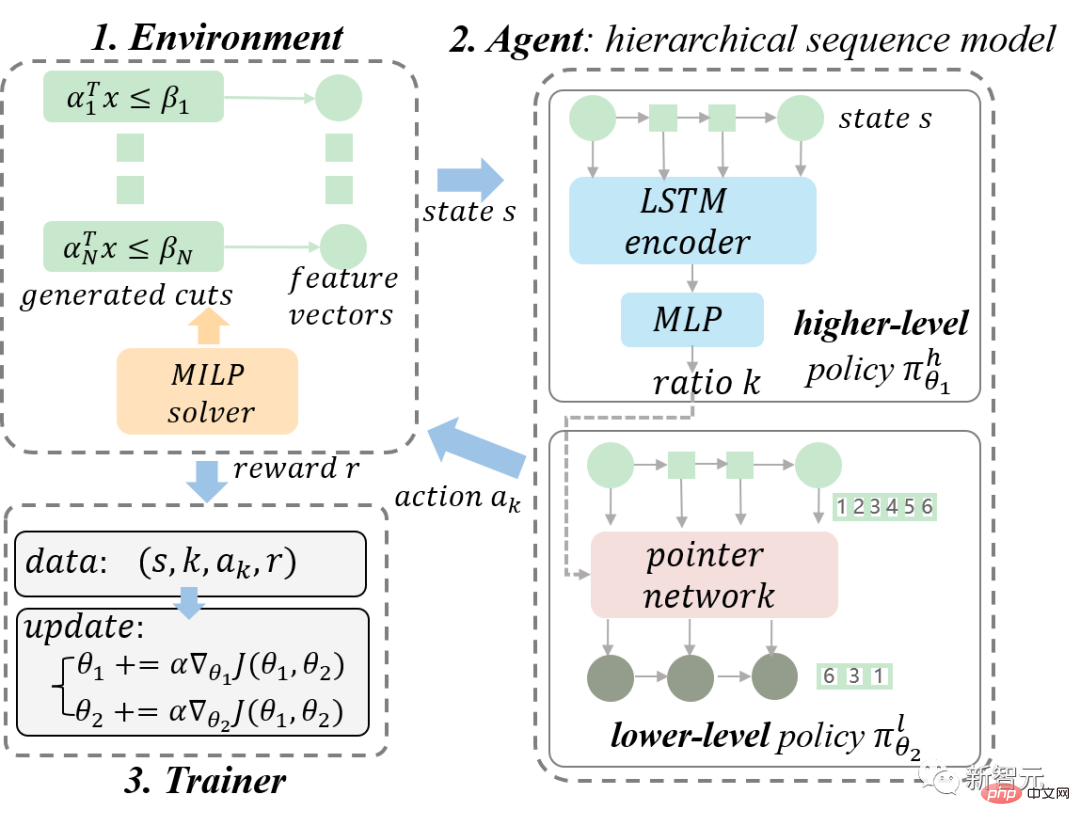
Figure 3. Schéma de notre cadre RL global proposé. Nous modélisons le solveur MILP comme l'environnement et le modèle HEM comme l'agent. Nous collectons des données de formation grâce à une interaction continue entre l'agent et l'environnement, et formons le modèle HEM à l'aide d'un gradient de politique hiérarchique.
3.1 Modélisation du problème
Espace d'état : étant donné que la relaxation LP actuelle et les coupes candidates générées contiennent les informations de base de la sélection du plan de coupe, nous définissons l'état. Représente ici le modèle mathématique de la relaxation LP actuelle, représente l'ensemble des plans de coupe candidats et représente la solution optimale de relaxation LP. Afin de coder les informations d'état, nous concevons 13 fonctionnalités pour chaque plan de coupe candidat en fonction des informations. Autrement dit, nous représentons les états à travers un vecteur de caractéristiques à 13 dimensions. Veuillez consulter le chapitre 4 de l'article original pour plus de détails.
Espace d'action : Afin de considérer à la fois la proportion et l'ordre des coupes sélectionnées, nous définissons l'espace d'action comme tous les sous-ensembles ordonnés de l'ensemble des coupes candidates.
Fonction de récompense : afin d'évaluer l'impact de l'ajout d'une coupe sur la résolution du MILP, nous pouvons utiliser le temps de solution, l'intégrale d'écart primal-double et l'amélioration de la double limite. Veuillez consulter le chapitre 4 de l'article original pour plus de détails.
Fonction de transition : la fonction de transfert génère l'état suivant en fonction de l'état actuel et de l'action entreprise. La fonction de transfert dans la tâche de sélection du plan de coupe est implicitement fournie par le solveur.
Pour plus de détails sur la modélisation, veuillez consulter le chapitre 4 de l'article original.
3.2 Modèle de politique : modèle de séquence hiérarchique
Comme le montre la figure 3, nous modélisons le solveur MILP en tant qu'environnement et le HEM en tant qu'agent. Le modèle HEM proposé est présenté en détail ci-dessous. Afin de faciliter la lecture, nous simplifions la motivation de la méthode et nous concentrons sur une explication claire de la mise en œuvre de la méthode. Les lecteurs intéressés sont invités à se référer au chapitre 4 de l'article original pour les détails pertinents.
Comme le montre le module Agent de la figure 3, HEM se compose de modèles de politique supérieur et inférieur. Les modèles de couche supérieure et inférieure apprennent respectivement la politique de couche supérieure (politique) et la politique de couche inférieure.
Tout d'abord, la politique de niveau supérieur apprend le nombre de coupes qui doivent être sélectionnées en prédisant la proportion appropriée. En supposant que la longueur de l'état est et que le rapport de prédiction est , alors le nombre de coupes qui doivent être sélectionnées pour la prédiction est 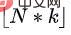
, où 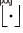 représente la fonction d'arrondi vers le bas. Nous définissons
représente la fonction d'arrondi vers le bas. Nous définissons  .
.
Deuxièmement, la politique de niveau inférieur apprend à sélectionner un sous-ensemble ordonné d'une taille donnée. La politique de niveau inférieur peut être définie 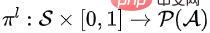 , où
, où 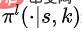 représente la distribution de probabilité sur l'espace d'action étant donné l'état S et la proportion K. Plus précisément, nous modélisons la politique sous-jacente sous la forme d’un modèle séquence à séquence (modèle séquentiel).
représente la distribution de probabilité sur l'espace d'action étant donné l'état S et la proportion K. Plus précisément, nous modélisons la politique sous-jacente sous la forme d’un modèle séquence à séquence (modèle séquentiel).
Enfin, la stratégie de sélection de coupe est dérivée de la loi de probabilité totale, c'est-à-dire
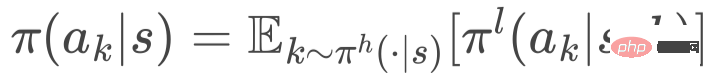
3.3 Méthode d'entraînement : gradient de stratégie hiérarchique
Étant donné la fonction objectif d'optimisation
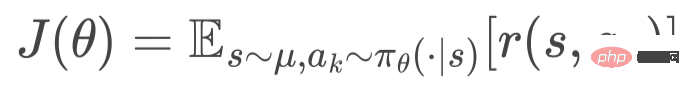
Figure 4 . Dégradé de stratégie hiérarchique. Nous optimisons le modèle HEM de cette manière stochastique par descente de gradient.
4 Introduction à l'expérience
Notre expérience comprend cinq parties principales :
Expérience 1. Évaluez notre méthode sur 3 problèmes MILP générés artificiellement et 6 références de problèmes MILP difficiles provenant de différents domaines d'application.
Expérience 2. Menez une expérience d'ablation soigneusement conçue pour fournir des informations approfondies sur l'HEM.
Expérience 3. Testez les performances de généralisation de HEM pour la taille du problème.
Expérience 4. Visualisez les caractéristiques des plans de coupe sélectionnés par notre méthode et notre base de référence.
Expérience 5. Déployer notre méthode sur le problème réel de planification de production de Huawei pour vérifier la supériorité de HEM.
Nous présentons uniquement l'expérience 1 dans cet article. Pour plus de résultats expérimentaux, veuillez consulter le chapitre 5 de l'article original. Veuillez noter que tous les résultats expérimentaux rapportés dans notre article sont des résultats obtenus sur la base d'une formation avec le code de la version PyTorch.
Les résultats de l'expérience 1 sont présentés dans le tableau 1. Nous avons comparé les résultats de HEM et de 6 références sur 9 ensembles de données open source. Les résultats expérimentaux montrent que HEM peut améliorer l’efficacité de résolution d’environ 20 % en moyenne.
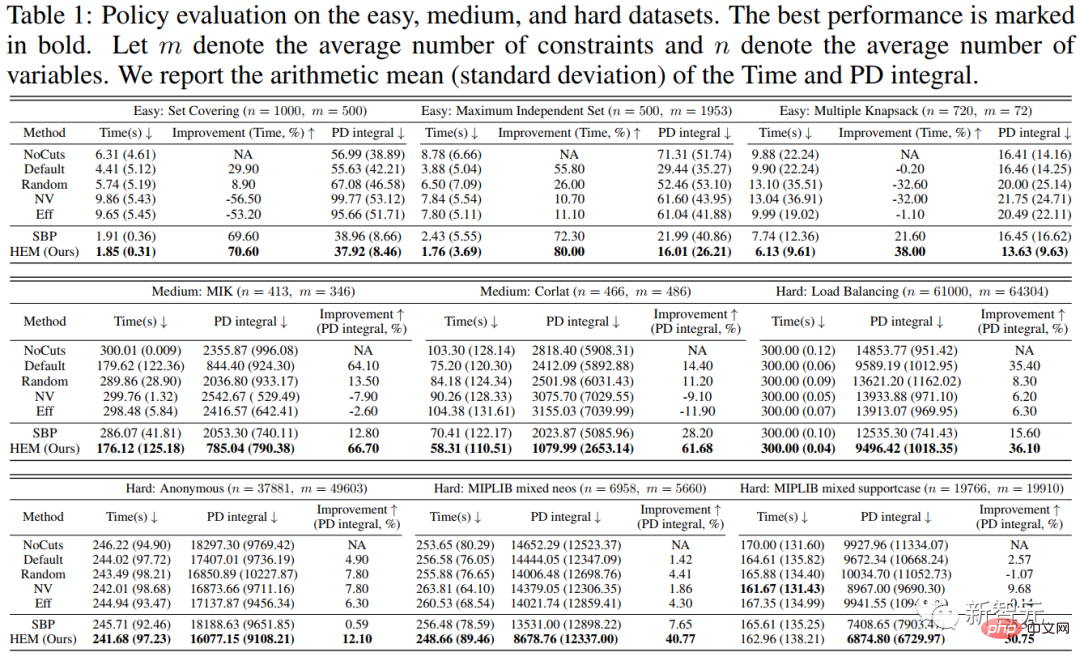
Figure 5. Évaluation de la stratégie sur des ensembles de données faciles, moyens et durs. Les performances optimales sont indiquées en gras. Soit m représente le nombre moyen de contraintes et n représente le nombre moyen de variables. Nous montrons la moyenne arithmétique (écart type) des temps de solution et des intégrales d'espacement primal-dual.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Il existe de nombreuses raisons pour lesquelles la startup MySQL échoue, et elle peut être diagnostiquée en vérifiant le journal des erreurs. Les causes courantes incluent les conflits de port (vérifier l'occupation du port et la configuration de modification), les problèmes d'autorisation (vérifier le service exécutant les autorisations des utilisateurs), les erreurs de fichier de configuration (vérifier les paramètres des paramètres), la corruption du répertoire de données (restaurer les données ou reconstruire l'espace de la table), les problèmes d'espace de la table InNODB (vérifier les fichiers IBDATA1), la défaillance du chargement du plug-in (vérification du journal des erreurs). Lors de la résolution de problèmes, vous devez les analyser en fonction du journal d'erreur, trouver la cause profonde du problème et développer l'habitude de sauvegarder régulièrement les données pour prévenir et résoudre des problèmes.
 Mysql peut-il renvoyer JSON
Apr 08, 2025 pm 03:09 PM
Mysql peut-il renvoyer JSON
Apr 08, 2025 pm 03:09 PM
MySQL peut renvoyer les données JSON. La fonction JSON_Extract extrait les valeurs de champ. Pour les requêtes complexes, envisagez d'utiliser la clause pour filtrer les données JSON, mais faites attention à son impact sur les performances. Le support de MySQL pour JSON augmente constamment, et il est recommandé de faire attention aux dernières versions et fonctionnalités.
 Comprendre les propriétés acides: les piliers d'une base de données fiable
Apr 08, 2025 pm 06:33 PM
Comprendre les propriétés acides: les piliers d'une base de données fiable
Apr 08, 2025 pm 06:33 PM
Une explication détaillée des attributs d'acide de base de données Les attributs acides sont un ensemble de règles pour garantir la fiabilité et la cohérence des transactions de base de données. Ils définissent comment les systèmes de bases de données gérent les transactions et garantissent l'intégrité et la précision des données même en cas de plantages système, d'interruptions d'alimentation ou de plusieurs utilisateurs d'accès simultanément. Présentation de l'attribut acide Atomicité: une transaction est considérée comme une unité indivisible. Toute pièce échoue, la transaction entière est reculée et la base de données ne conserve aucune modification. Par exemple, si un transfert bancaire est déduit d'un compte mais pas augmenté à un autre, toute l'opération est révoquée. BeginTransaction; UpdateAccountSsetBalance = Balance-100Wh
 Master SQL Limit Clause: Contrôlez le nombre de lignes dans une requête
Apr 08, 2025 pm 07:00 PM
Master SQL Limit Clause: Contrôlez le nombre de lignes dans une requête
Apr 08, 2025 pm 07:00 PM
Clause SQLLIMIT: Contrôlez le nombre de lignes dans les résultats de la requête. La clause limite dans SQL est utilisée pour limiter le nombre de lignes renvoyées par la requête. Ceci est très utile lors du traitement de grands ensembles de données, des affichages paginés et des données de test, et peut améliorer efficacement l'efficacité de la requête. Syntaxe de base de la syntaxe: selectColumn1, Column2, ... FromTable_NamelimitNumber_Of_Rows; Number_OF_ROWS: Spécifiez le nombre de lignes renvoyées. Syntaxe avec décalage: selectColumn1, Column2, ... FromTable_Namelimitoffset, numéro_of_rows; décalage: sauter
 Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Guide d'optimisation des performances de la base de données MySQL dans les applications à forte intensité de ressources, la base de données MySQL joue un rôle crucial et est responsable de la gestion des transactions massives. Cependant, à mesure que l'échelle de l'application se développe, les goulots d'étranglement des performances de la base de données deviennent souvent une contrainte. Cet article explorera une série de stratégies efficaces d'optimisation des performances MySQL pour garantir que votre application reste efficace et réactive dans des charges élevées. Nous combinerons des cas réels pour expliquer les technologies clés approfondies telles que l'indexation, l'optimisation des requêtes, la conception de la base de données et la mise en cache. 1. La conception de l'architecture de la base de données et l'architecture optimisée de la base de données sont la pierre angulaire de l'optimisation des performances MySQL. Voici quelques principes de base: sélectionner le bon type de données et sélectionner le plus petit type de données qui répond aux besoins peut non seulement économiser un espace de stockage, mais également améliorer la vitesse de traitement des données.
 La clé principale de MySQL peut être nul
Apr 08, 2025 pm 03:03 PM
La clé principale de MySQL peut être nul
Apr 08, 2025 pm 03:03 PM
La clé primaire MySQL ne peut pas être vide car la clé principale est un attribut de clé qui identifie de manière unique chaque ligne dans la base de données. Si la clé primaire peut être vide, l'enregistrement ne peut pas être identifié de manière unique, ce qui entraînera une confusion des données. Lorsque vous utilisez des colonnes entières ou des UUIdes auto-incrémentales comme clés principales, vous devez considérer des facteurs tels que l'efficacité et l'occupation de l'espace et choisir une solution appropriée.
 Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Il est impossible de visualiser le mot de passe MongoDB directement via NAVICAT car il est stocké sous forme de valeurs de hachage. Comment récupérer les mots de passe perdus: 1. Réinitialiser les mots de passe; 2. Vérifiez les fichiers de configuration (peut contenir des valeurs de hachage); 3. Vérifiez les codes (May Code Hardcode).
 Surveillez les gouttelettes MySQL et MariaDB avec Exportateur de Prometheus Mysql
Apr 08, 2025 pm 02:42 PM
Surveillez les gouttelettes MySQL et MariaDB avec Exportateur de Prometheus Mysql
Apr 08, 2025 pm 02:42 PM
Une surveillance efficace des bases de données MySQL et MARIADB est essentielle pour maintenir des performances optimales, identifier les goulots d'étranglement potentiels et assurer la fiabilité globale du système. Prometheus Mysql Exportateur est un outil puissant qui fournit des informations détaillées sur les mesures de base de données qui sont essentielles pour la gestion et le dépannage proactifs.





