 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Analyse du timing Guerrier du Pentagone ! L'Université Tsinghua propose TimesNet : leader en matière de prédiction, de remplissage, de classification et de détection
Analyse du timing Guerrier du Pentagone ! L'Université Tsinghua propose TimesNet : leader en matière de prédiction, de remplissage, de classification et de détection
Analyse du timing Guerrier du Pentagone ! L'Université Tsinghua propose TimesNet : leader en matière de prédiction, de remplissage, de classification et de détection
Atteindre la polyvalence des tâches est une question centrale dans la recherche de modèles de base d'apprentissage profond, et constitue également l'une des principales préoccupations dans l'orientation récente des grands modèles.
Cependant, dans le domaine des séries chronologiques, les différents types de tâches d'analyse varient considérablement, notamment les tâches de prédiction qui nécessitent une modélisation fine et les tâches de classification qui nécessitent l'extraction d'informations sémantiques de haut niveau. Comment créer un modèle de base profond unifié pour effectuer efficacement diverses tâches d'analyse temporelleIl n'y avait pas de solution établie auparavant.
À cette fin, une équipe de l'École de logiciel de l'Université Tsinghua a mené des recherches sur la question fondamentale de la modélisation des changements de timing et a proposé TimesNet, un modèle de base de timing universel pour les tâches. Le document a été accepté par l'ICLR 2023.

Liste des auteurs : Wu Haixu*, Hu Tenge*, Liu Yong*, Zhou Hang, Wang Jianmin, Long Mingsheng
Lien : https://openreview.net/pdf ?id=ju_Uqw384Oq
Code : https://github.com/thuml/TimesNet
Bibliothèque d'algorithmes de séries temporelles : https://github.com/thuml/Time-Series-Library
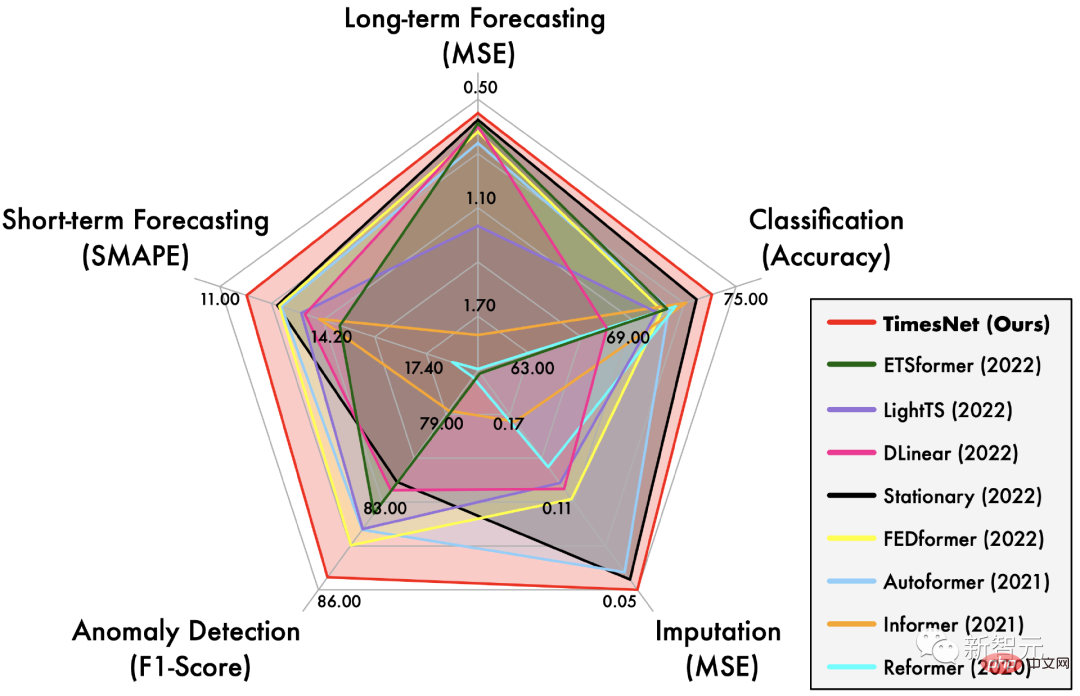
TimesNet Il a atteint un leadership complet dans les cinq tâches principales que sont la prévision à long terme et à court terme, le remplissage des valeurs manquantes, la détection des anomalies et la classification.
1 Analyse du problème
Différent du langage naturel, de la vidéo et d'autres données de séquence, seuls certains scalaires sont enregistrés à un seul instant de la série chronologique, et ses informations clés sont davantage contenues dans la variation temporelle (Variation temporelle) milieu.
Par conséquent, La modélisation des changements de timing est un problème central commun à tous les types de tâches d'analyse de timing.
Ces dernières années, divers modèles profonds ont été largement utilisés dans les tâches d'analyse temporelle, tels que les réseaux de neurones récurrents (RNN), les réseaux convolutifs temporels (TCN) et les réseaux de transformateurs (Transformer).
Cependant, les deux premiers types de méthodes se concentrent principalement sur la capture des changements entre des instants proches et ont des capacités de modélisation insuffisantes pour les dépendances à long terme.
Bien que Transformer présente des avantages naturels dans la modélisation des dépendances à long terme, en raison des changements de timing extrêmement complexes dans le monde réel, il est difficile d'exploiter des dépendances de timing fiables uniquement en s'appuyant sur l'attention entre des points temporels discrets.
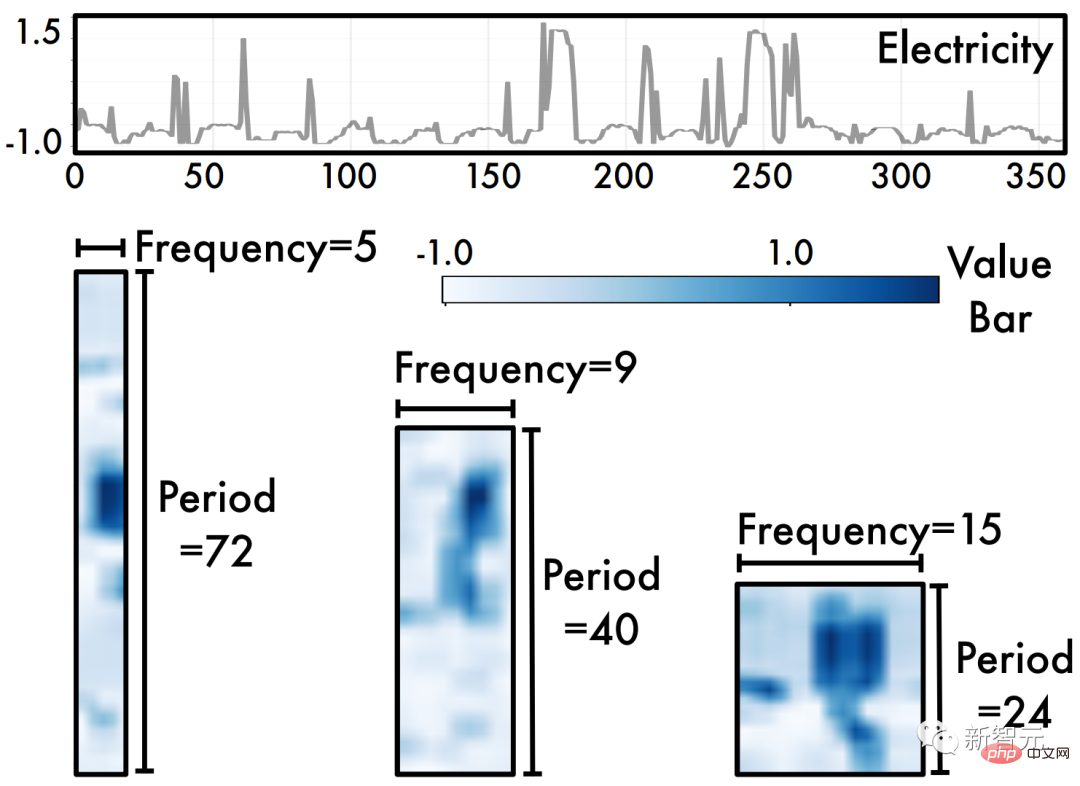
À cette fin, cet article analyse les changements de timing dans une nouvelle perspective multi-périodicité, comme le montre la figure ci-dessous. On observe que :
- les séries temporelles sont naturellement multi-périodiques.
Les données de séries chronologiques dans le monde réel sont souvent la superposition de différents processus périodiques. Par exemple, les données de trafic changent quotidiennement à court terme, alors qu'à long terme elles changent de manière hebdomadaire. Ces données de différentes périodes se chevauchent et interfèrent les unes avec les autres, ce qui pose de grands défis à l'analyse des séries chronologiques.
- La série chronologique présente deux types de changements de séries chronologiques au sein du cycle et entre les cycles.
Plus précisément, pour le processus d'une certaine période, le changement à chaque instant est non seulement lié au moment adjacent, mais également fortement lié à des processus similaires dans la période adjacente. Parmi eux, les changements intra-cycles correspondent à des processus à court terme, tandis que les changements inter-cycles peuvent refléter des tendances à long terme dans des cycles consécutifs. Remarque : Si la série chronologique n'a pas de périodicité évidente, cela équivaut à la situation où la période est infiniment longue.
2 Idées de conception
Sur la base des deux observations ci-dessus, nous avons conçu la structure de TimesNet comme suit :
La- multi-périodicité des séries temporelles a naturellement inspiré une idée de conception modulaire, c'est-à-dire qu'un module capture les changements de séries chronologiques dominés par une période spécifique. Cette idée de conception modulaire peut découpler des changements de temps complexes, ce qui est bénéfique pour la modélisation ultérieure. Pour les
- changements intra-cycles et inter-cycles des séries chronologiques, cet article propose de manière innovanteétendre les données de séries chronologiques unidimensionnelles à un espace bidimensionnel pour analyse. Comme le montre la figure ci-dessus, en repliant une série temporelle unidimensionnelle basée sur plusieurs cycles, plusieurs tenseurs bidimensionnels (tenseurs 2D) peuvent être obtenus. Les colonnes et les lignes de chaque tenseur bidimensionnel reflètent la série temporelle au sein du cycle. et entre les cycles respectivement, c'est-à-dire que nous obtenons des Variations temporelles 2D.
Par conséquent, après avoir plié les données de séries chronologiques, nous pouvons directement utiliser le
Visual Backbone Networkavancé pour effectuer une extraction de fonctionnalités sur les données de séries chronologiques, telles que Swin Transformer, ResNeXt, ConvNeXt, etc. Cette conception permet également aux tâches d'analyse temporelle de bénéficier directement du domaine en plein essor de la vision par ordinateur. 3 TimesNet
Sur la base des idées ci-dessus, nous avons proposé le modèle TimesNet, qui décompose les changements de séries chronologiques complexes en différents cycles via une structure modulaire, et réalise une modélisation intra-cycle et unifiée des variations hebdomadaires
.Dans cette section, nous présenterons d'abord la méthode d'extension des données de séries chronologiques à un espace bidimensionnel, puis présenterons l'architecture globale du modèle.
3.1 Changements de timing : 1D->2D
Le processus de pliage chronométré est illustré dans la figure ci-dessus, qui est principalement divisé en deux étapes suivantes :
(1) Extraction du cycle
pour Une série temporelle unidimensionnelle avec une longueur temporelle de et une dimension de canal de , peut extraire directement des informations périodiques grâce à la transformée de Fourier rapide (FFT) de la dimension temporelle, c'est-à-dire :
où représente l'intensité de chaque composante de fréquence dans , la fréquence avec la plus grande intensité correspond à la durée de la période la plus significative. 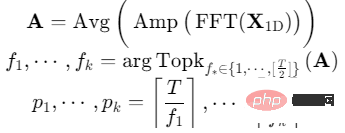
(2) Pliage de séquence 1D->2D
Pour les périodes sélectionnées, la série temporelle unidimensionnelle originale est pliée respectivement. Le processus peut être formalisé comme :
.
Parmi eux, le remplissage 0 à la fin de la séquence rend la longueur de la séquence divisible. 
Grâce aux opérations ci-dessus, nous obtenons un ensemble de tenseurs bidimensionnels, qui correspondent à des changements de séries temporelles bidimensionnelles avec une période de .
3.2 Conception du modèle
L'architecture globale de TimesNet est illustrée dans la figure :
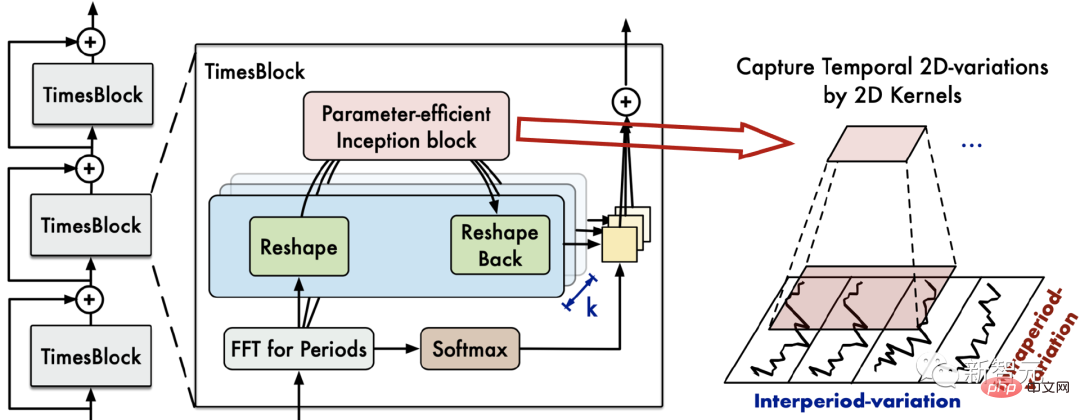 Dans l'ensemble, TimesNet se compose de TimesBlocks empilés. La séquence d'entrée passe d'abord par la couche d'intégration pour obtenir des fonctionnalités profondes. Pour la couche TimesBlock, son entrée est et sa sortie est :
Dans l'ensemble, TimesNet se compose de TimesBlocks empilés. La séquence d'entrée passe d'abord par la couche d'intégration pour obtenir des fonctionnalités profondes. Pour la couche TimesBlock, son entrée est et sa sortie est :
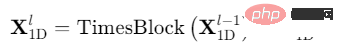
Plus précisément, comme le montre la figure ci-dessous, chaque TimesBlock contient les sous-processus suivants :
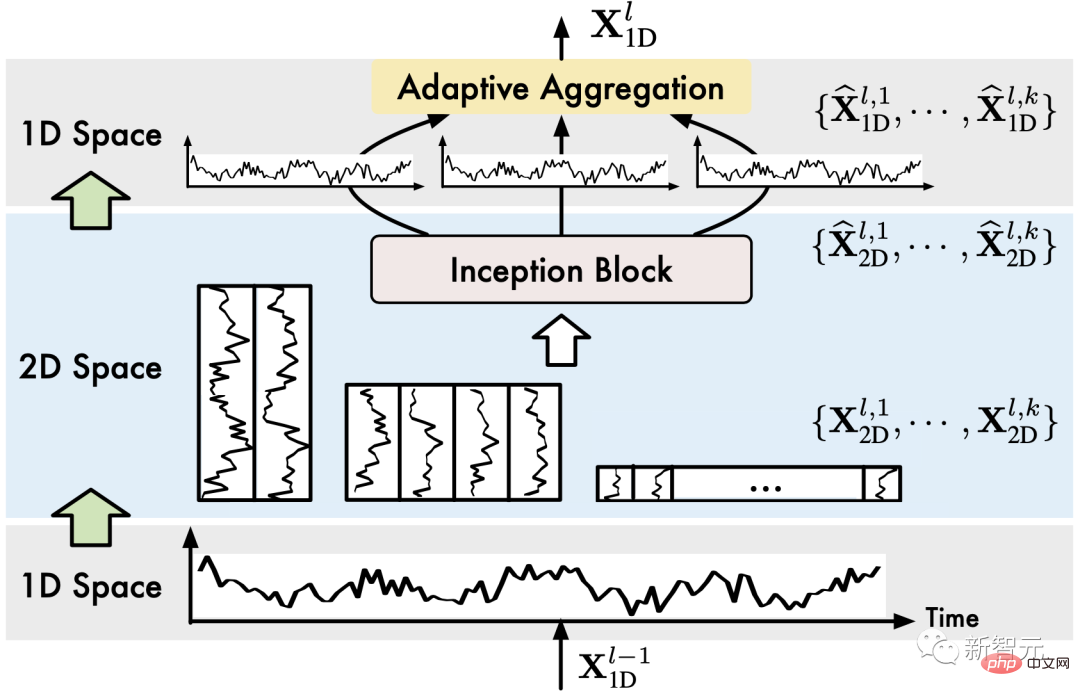
(1) Pliage des séries temporelles (1D->2D) : TimesBlock d'abord, les fonctionnalités de série chronologique unidimensionnelle d'entrée extraient le cycle, puis le convertissent en changements de séries chronologiques bidimensionnelles, ce qui a été abordé dans la section précédente :
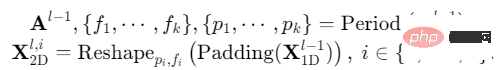
(2) Extraire les données bidimensionnelles représentation des changements de séries chronologiques (représentation 2D) : comme analysé précédemment, les changements de séries chronologiques bidimensionnels convertis ont une localité 2D, de sorte que la convolution 2D peut être utilisée directement pour extraire des caractéristiques. Ici, nous avons choisi le modèle Inception classique, à savoir :
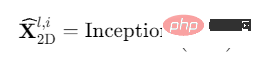
Il est à noter que parce que nous avons converti des caractéristiques temporelles 1D en espace 2D, nous pouvons également utiliser de nombreux modèles de pointe dans le domaine de l'informatique. vision, par exemple, ResNeXt, ConvNeXt, Attention-based Swin Transformer, etc. Cela permet à l’analyse des séries chronologiques de fonctionner main dans la main avec le réseau fédérateur visuel. ⋅ Supprimez le 0 ajouté par l'opération Padding (⋅) à l'étape (1).
(4) Fusion adaptative (agrégation 1D) : Afin de fusionner des informations multipériodes, nous effectuons une sommation pondérée des représentations de séries chronologiques bidimensionnelles extraites, et le poids de sommation sélectionné est obtenu à l'étape ( 1) L'intensité de fréquence correspondante :
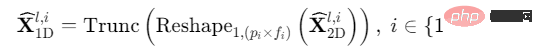
En convertissant une série chronologique 1D en une conception spatiale 2D, TimesNet réalise la construction de changements de séries chronologiques de "plusieurs périodes pour extraire séparément les changements de séries chronologiques bidimensionnelles, puis effectuer un processus de moulage par fusion adaptative.
4 Expériences
Nous avons mené des expériences sur cinq tâches principales : prédiction à long terme, prédiction à court terme, remplissage des valeurs manquantes, détection d'anomalies et classification, couvrant 36 ensembles de données et 81 paramètres expérimentaux différents.
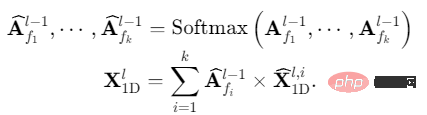
Dans le même temps, 19 méthodes approfondies différentes ont été comparées, y compris les derniers modèles basés sur RNN, CNN, MLP et Transformer, tels que N-BEATS (2019), Autoformer (2021), LSSL (2022) ), N-Hits (2022), FEDformer (2022), Dlinear (2023), etc.
4.1 Résultats globaux
Comme le montre le graphique radar d'ouverture, TimesNet a atteint SOTA sur les cinq tâches. 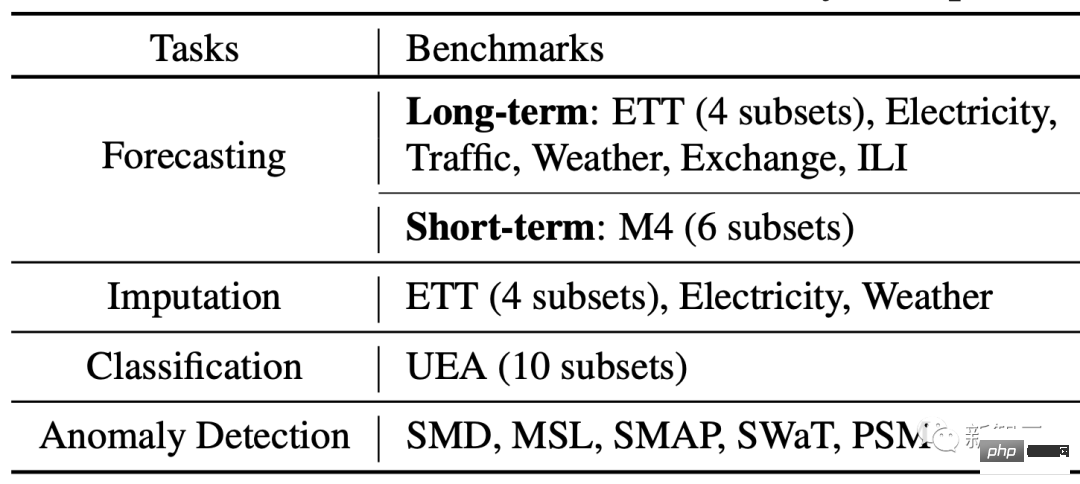
(1) Prédiction à long terme : dans cette tâche de grande envergure, TimesNet surpasse les modèles de pointe basés sur Transformer et MLP.
(2) Prédiction à court terme : L'ensemble de données M4 utilisé dans cette expérience contient 6 sous-ensembles de données avec différentes fréquences d'échantillonnage, avec un total de plus de 100 000 éléments de données. TimesNet a néanmoins obtenu des résultats optimaux dans cette situation complexe de distribution de données, en vérifiant les capacités de modélisation des changements temporels du modèle.

(3) Tâche de classification : Dans cette tâche, TimesNet a surpassé l'algorithme classique de Rocket et le modèle d'apprentissage en profondeur de pointe Flowformer.
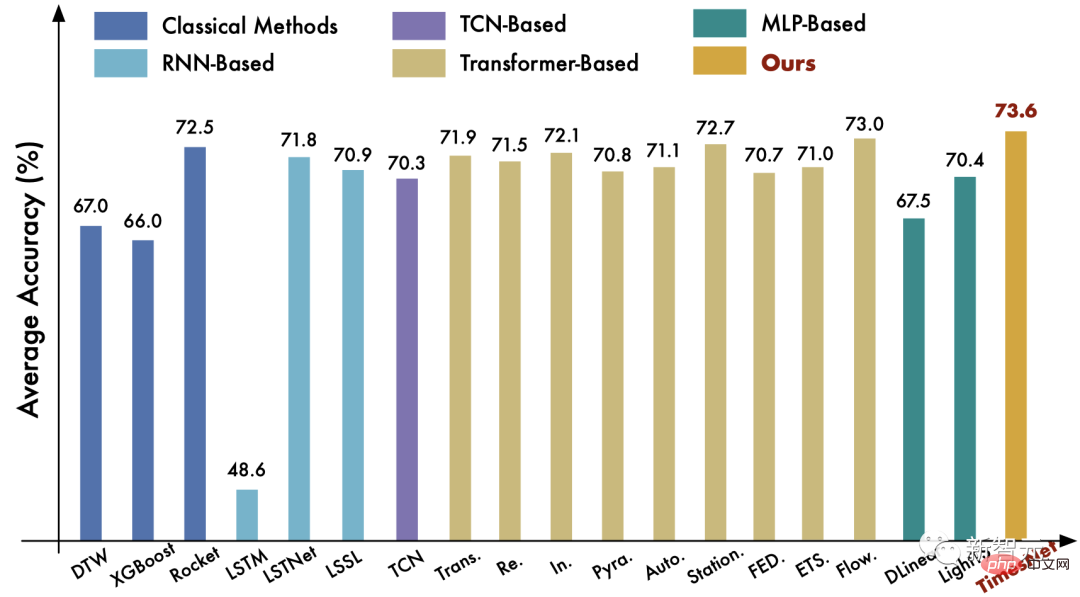
Veuillez consulter le document pour plus de comparaisons de tâches.
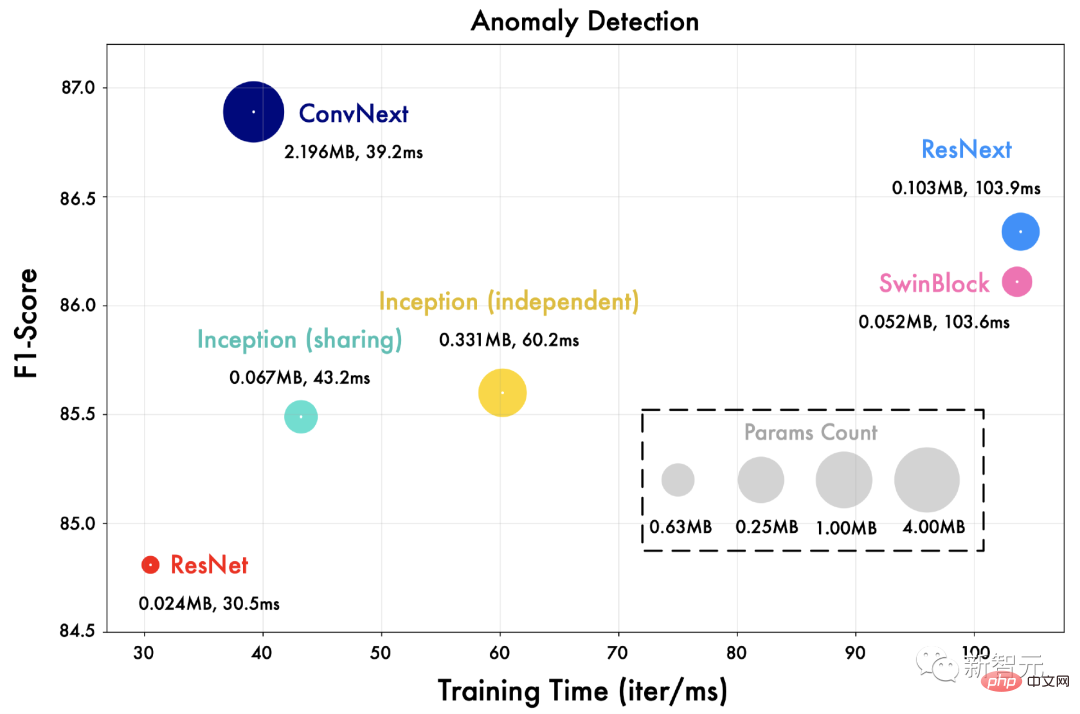
4.2 Généralisation du réseau fédérateur visuel
Nous remplaçons le réseau Inception dans TimesNet par différents réseaux fédérateurs visuels, tels que ResNet, ConvNext, Swin Transformer, etc.
Comme le montre la figure ci-dessous, un réseau fédérateur visuel plus avancé peut apporter de meilleurs résultats. Cela signifie également que dans le cadre de TimesNet, l’analyse des séries chronologiques peut directement bénéficier des avancées dans le domaine des réseaux fédérateurs visuels.
4.3 Analyse de représentation
Afin d'explorer davantage la source de l'effet TimesNet, nous montrons la relation entre "la similarité CKA entre la couche inférieure du modèle et la représentation de la couche supérieure" et "effet de modèle". Parmi eux, plus la similarité CKA est faible, plus la différence de représentation entre la couche inférieure et la couche supérieure du modèle est grande, c'est-à-dire une représentation plus hiérarchique. À partir de la visualisation ci-dessus, nous pouvons observer : , cela indique que la tâche nécessite des représentations de niveau inférieur ;
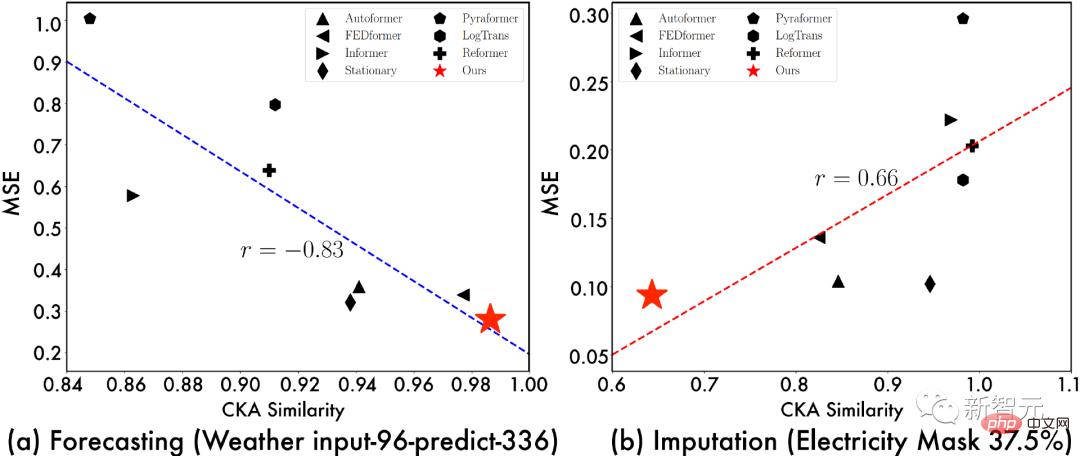
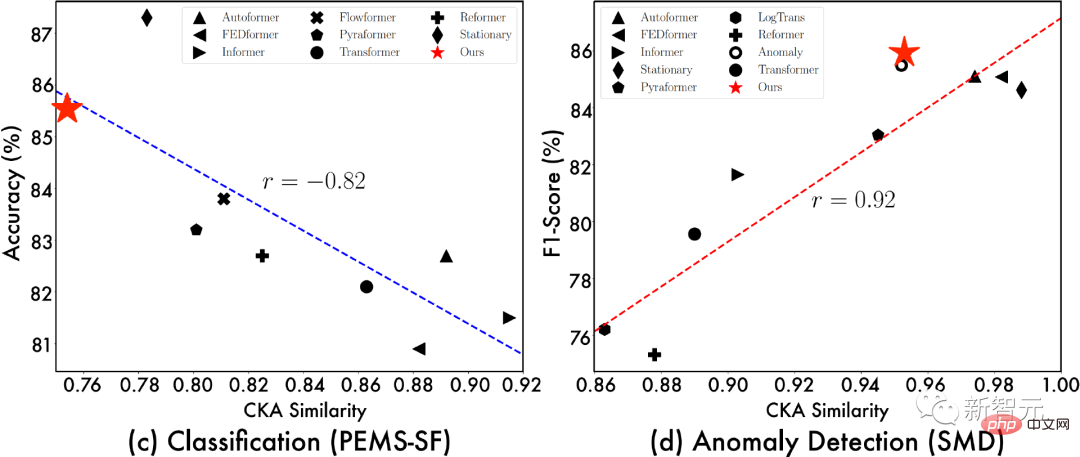
Dans le même temps, l'analyse de représentation ci-dessus fournit également des idées de conception de modèles profonds pour des tâches spécifiques. Par exemple, pour les tâches de prédiction, nous devons nous concentrer sur l'extraction de fonctionnalités sous-jacentes à granularité fine, et pour les tâches de remplissage, nous devons réfléchir davantage à l’apprentissage des représentations globales.
- 5 RésuméInspiré par la nature multipériode des séries chronologiques, cet article propose un modèle de base pour l'analyse des séries chronologiques qui est universel pour les tâches - TimesNet. Ce modèle plie de manière innovante les séries chronologiques unidimensionnelles dans un espace bidimensionnel et utilise la convolution 2D pour obtenir des caractéristiques de séries chronologiques. Cette innovation permet aux tâches d’analyse temporelle de bénéficier directement du réseau fédérateur visuel en plein essor, ce qui est très inspirant pour les recherches ultérieures.
- Dans le même temps, TimesNet a atteint un leadership complet dans les cinq tâches principales d'analyse de séries chronologiques que sont la prévision à long terme et à court terme, le remplissage des valeurs manquantes, la détection des anomalies et la classification, et possède une excellente valeur d'application.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Imaginez un modèle d'intelligence artificielle qui non seulement a la capacité de surpasser l'informatique traditionnelle, mais qui permet également d'obtenir des performances plus efficaces à moindre coût. Ce n'est pas de la science-fiction, DeepSeek-V2[1], le modèle MoE open source le plus puissant au monde est ici. DeepSeek-V2 est un puissant mélange de modèle de langage d'experts (MoE) présentant les caractéristiques d'une formation économique et d'une inférence efficace. Il est constitué de 236B paramètres, dont 21B servent à activer chaque marqueur. Par rapport à DeepSeek67B, DeepSeek-V2 offre des performances plus élevées, tout en économisant 42,5 % des coûts de formation, en réduisant le cache KV de 93,3 % et en augmentant le débit de génération maximal à 5,76 fois. DeepSeek est une entreprise explorant l'intelligence artificielle générale
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L’IA change effectivement les mathématiques. Récemment, Tao Zhexuan, qui a prêté une attention particulière à cette question, a transmis le dernier numéro du « Bulletin de l'American Mathematical Society » (Bulletin de l'American Mathematical Society). En se concentrant sur le thème « Les machines changeront-elles les mathématiques ? », de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, intense et passionnant. L'auteur dispose d'une équipe solide, comprenant Akshay Venkatesh, lauréat de la médaille Fields, le mathématicien chinois Zheng Lejun, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur. Le monde de l’IA a radicalement changé. Vous savez, bon nombre de ces articles ont été soumis il y a un an.
 Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas entre officiellement dans l’ère des robots électriques ! Hier, l'Atlas hydraulique s'est retiré "en larmes" de la scène de l'histoire. Aujourd'hui, Boston Dynamics a annoncé que l'Atlas électrique était au travail. Il semble que dans le domaine des robots humanoïdes commerciaux, Boston Dynamics soit déterminé à concurrencer Tesla. Après la sortie de la nouvelle vidéo, elle a déjà été visionnée par plus d’un million de personnes en seulement dix heures. Les personnes âgées partent et de nouveaux rôles apparaissent. C'est une nécessité historique. Il ne fait aucun doute que cette année est l’année explosive des robots humanoïdes. Les internautes ont commenté : Les progrès des robots ont fait ressembler la cérémonie d'ouverture de cette année à des êtres humains, et le degré de liberté est bien plus grand que celui des humains. Mais n'est-ce vraiment pas un film d'horreur ? Au début de la vidéo, Atlas est allongé calmement sur le sol, apparemment sur le dos. Ce qui suit est à couper le souffle
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Les performances de JAX, promu par Google, ont dépassé celles de Pytorch et TensorFlow lors de récents tests de référence, se classant au premier rang sur 7 indicateurs. Et le test n’a pas été fait sur le TPU présentant les meilleures performances JAX. Bien que parmi les développeurs, Pytorch soit toujours plus populaire que Tensorflow. Mais à l’avenir, des modèles plus volumineux seront peut-être formés et exécutés sur la base de la plate-forme JAX. Modèles Récemment, l'équipe Keras a comparé trois backends (TensorFlow, JAX, PyTorch) avec l'implémentation native de PyTorch et Keras2 avec TensorFlow. Premièrement, ils sélectionnent un ensemble de
 FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
La détection de cibles est un problème relativement mature dans les systèmes de conduite autonome, parmi lesquels la détection des piétons est l'un des premiers algorithmes à être déployés. Des recherches très complètes ont été menées dans la plupart des articles. Cependant, la perception de la distance à l’aide de caméras fisheye pour une vue panoramique est relativement moins étudiée. En raison de la distorsion radiale importante, la représentation standard du cadre de délimitation est difficile à mettre en œuvre dans les caméras fisheye. Pour alléger la description ci-dessus, nous explorons les conceptions étendues de boîtes englobantes, d'ellipses et de polygones généraux dans des représentations polaires/angulaires et définissons une métrique de segmentation d'instance mIOU pour analyser ces représentations. Le modèle fisheyeDetNet proposé avec une forme polygonale surpasse les autres modèles et atteint simultanément 49,5 % de mAP sur l'ensemble de données de la caméra fisheye Valeo pour la conduite autonome.
 Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
La dernière vidéo du robot Optimus de Tesla est sortie, et il peut déjà fonctionner en usine. À vitesse normale, il trie les batteries (les batteries 4680 de Tesla) comme ceci : Le responsable a également publié à quoi cela ressemble à une vitesse 20 fois supérieure - sur un petit "poste de travail", en sélectionnant et en sélectionnant et en sélectionnant : Cette fois, il est publié L'un des points forts de la vidéo est qu'Optimus réalise ce travail en usine, de manière totalement autonome, sans intervention humaine tout au long du processus. Et du point de vue d'Optimus, il peut également récupérer et placer la batterie tordue, en se concentrant sur la correction automatique des erreurs : concernant la main d'Optimus, le scientifique de NVIDIA Jim Fan a donné une évaluation élevée : la main d'Optimus est l'un des robots à cinq doigts du monde. le plus adroit. Ses mains ne sont pas seulement tactiles
 Une seule carte exécute Llama 70B plus rapidement que deux cartes, Microsoft vient de mettre le FP6 dans l'Open source A100 |
Apr 29, 2024 pm 04:55 PM
Une seule carte exécute Llama 70B plus rapidement que deux cartes, Microsoft vient de mettre le FP6 dans l'Open source A100 |
Apr 29, 2024 pm 04:55 PM
Le FP8 et la précision de quantification inférieure en virgule flottante ne sont plus le « brevet » du H100 ! Lao Huang voulait que tout le monde utilise INT8/INT4, et l'équipe Microsoft DeepSpeed a commencé à exécuter FP6 sur A100 sans le soutien officiel de NVIDIA. Les résultats des tests montrent que la quantification FP6 de la nouvelle méthode TC-FPx sur A100 est proche ou parfois plus rapide que celle de INT4, et a une précision supérieure à celle de cette dernière. En plus de cela, il existe également une prise en charge de bout en bout des grands modèles, qui ont été open source et intégrés dans des cadres d'inférence d'apprentissage profond tels que DeepSpeed. Ce résultat a également un effet immédiat sur l'accélération des grands modèles : dans ce cadre, en utilisant une seule carte pour exécuter Llama, le débit est 2,65 fois supérieur à celui des cartes doubles. un





