 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Les mathématiques derrière le modèle de diffusion sont-elles trop difficiles à digérer ? Google le dit clairement avec une perspective unifiée
Les mathématiques derrière le modèle de diffusion sont-elles trop difficiles à digérer ? Google le dit clairement avec une perspective unifiée
Les mathématiques derrière le modèle de diffusion sont-elles trop difficiles à digérer ? Google le dit clairement avec une perspective unifiée
Ces derniers temps, la peinture IA est devenue très populaire.
Bien que vous soyez émerveillé par les capacités de peinture de l’IA, ce que vous ne savez peut-être pas, c’est que le modèle de diffusion y joue un rôle important. Prenons l'exemple du modèle populaire DALL·E 2 d'OpenAI. Entrez simplement un simple texte (invite) et il peut générer plusieurs images haute définition 1024*1024.
Peu de temps après l'annonce de DALL·E 2, Google a ensuite publié Imagen, un modèle d'IA texte-image qui peut générer des images réalistes de la scène à partir d'une description textuelle donnée.
Il y a quelques jours à peine, Stability.Ai a rendu public la dernière version du modèle d'image de génération de texte Stable Diffusion, et les images qu'il a générées ont atteint la qualité commerciale.
Depuis que Google a lancé DDPM en 2020, le modèle de diffusion est progressivement devenu un nouveau point chaud dans le domaine de la génération. Plus tard, OpenAI a lancé les modèles GLIDE, ADM-G, etc., ce qui a rendu le modèle de diffusion populaire.
De nombreux chercheurs pensent que le modèle de génération d'images texte basé sur le modèle de diffusion possède non seulement un petit nombre de paramètres, mais génère également des images de meilleure qualité et a le potentiel de remplacer le GAN.
Cependant, la formule mathématique derrière le modèle de diffusion a intimidé de nombreux chercheurs, et de nombreux chercheurs pensent qu'elle est beaucoup plus difficile à comprendre que la VAE et le GAN.
Récemment, un chercheur de Google Research a écrit un article "Comprendre les modèles de diffusion : une perspective unifiée". Cet article montre les principes mathématiques derrière le modèle de diffusion de manière extrêmement détaillée, dans le but de permettre à d'autres chercheurs de suivre et de comprendre. le modèle de diffusion. Ce qu’ils sont et comment ils fonctionnent. 
Adresse de l'article : https://arxiv.org/pdf/2208.11970.pdf Quant à savoir à quel point cet article est « mathématique », l'auteur le décrit ainsi : Nous et ses détails atroces) montre les mathématiques derrière ces modèles.
L'article est divisé en 6 parties, comprenant principalement des modèles génératifs ; ELBO, VAE et VAE hiérarchique ;

Ce qui suit est un extrait de l'article d'introduction :
Modèle générateur
Étant donné un échantillon d'observation x dans la distribution, le but du modèle génératif est d'apprendre ses véritables données distribution p( x) Modélisation. Une fois le modèle appris, nous pouvons générer de nouveaux échantillons. De plus, sous certaines formes, nous pouvons également utiliser des modèles d’apprentissage pour évaluer des observations ou des échantillons de données.
Il existe plusieurs directions importantes dans la littérature de recherche actuelle. Cet article ne les présente que brièvement à un niveau élevé. Elles incluent principalement : le GAN, qui modélise le processus d'échantillonnage de distributions complexes et apprend de manière contradictoire. Les modèles génératifs, que nous pouvons également appeler méthodes « basées sur la vraisemblance », peuvent attribuer une probabilité élevée aux échantillons de données observés et incluent généralement l'autorégression, le flux normalisé et la VAE. Modélisation basée sur l'énergie, dans cette approche, la distribution est apprise comme une fonction énergétique flexible arbitraire puis normalisée. Dans les modèles génératifs basés sur les scores, au lieu d’apprendre à modéliser la fonction énergétique elle-même, le score basé sur le modèle énergétique est appris sous forme d’un réseau neuronal.
Dans cette étude, cet article explore et passe en revue les modèles de diffusion, comme le montre l'article, ils ont des interprétations basées sur la vraisemblance et les scores.
Modèle de diffusion variationnel
De manière simple, un modèle de diffusion variationnel (VDM) peut être considéré comme une variation hiérarchique de Markov avec trois restrictions (ou hypothèses) principales. Divisées en auto-encodeurs (MHVAE), elles sont :
- La dimension latente est exactement la même que la dimension des données ;
- La structure de l'encodeur latent à chaque pas de temps n'est pas apprise, elle est prédéfinie comme un modèle gaussien linéaire. En d'autres termes, il s'agit d'une distribution gaussienne centrée sur la sortie du pas de temps précédent ; les paramètres gaussiens du codeur latent changent avec le temps, et la distribution latente au pas de temps final T du processus est une distribution quasi-gaussienne.
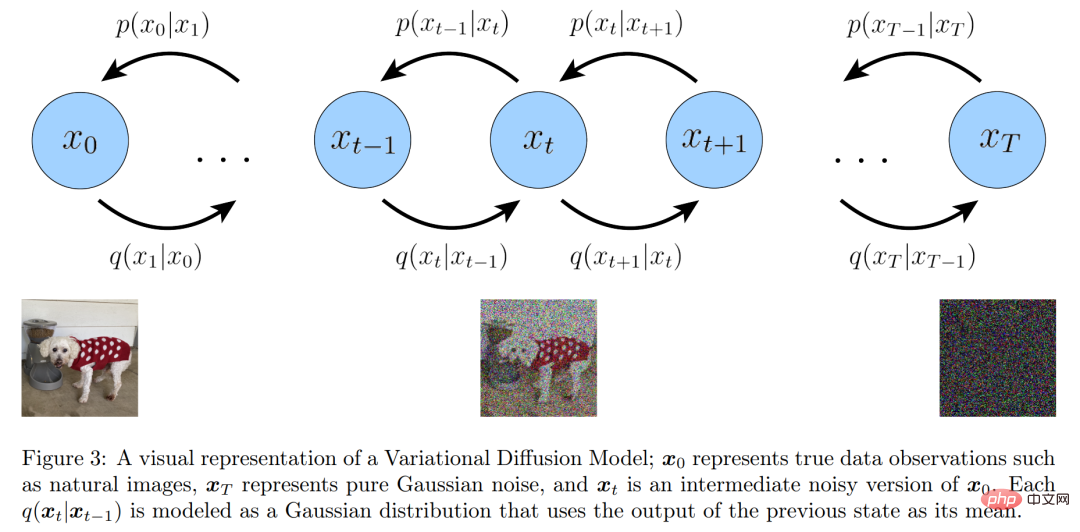 Représentation visuelle du modèle de diffusion variationnelle
Représentation visuelle du modèle de diffusion variationnelle
De plus, les chercheurs maintiennent explicitement la relation entre les transformations hiérarchiques à partir des auto-encodeurs variationnels hiérarchiques standard de Markov. Ils ont élargi une à une les implications des trois hypothèses principales ci-dessus.
À partir de la première hypothèse, en raison d'une mauvaise utilisation des symboles, les échantillons de données réelles et les variables latentes peuvent désormais être représentés par x_t, où t=0 représente les données réelles de l'échantillon et t ∈ [1, T] représente le variables latentes correspondantes, sa structure hiérarchique est indexée par t. Le postérieur VDM est le même que le postérieur MHVAE, mais peut maintenant être réécrit comme suit :
 De la deuxième hypothèse, on sait que la distribution de chaque variable latente dans l'encodeur est divisée par le précédent La variable latente de couche est une distribution gaussienne centrée. Contrairement à MHVAE, la structure du codeur à chaque pas de temps n'est pas apprise, elle est fixée comme un modèle gaussien linéaire, où la moyenne et l'écart type peuvent être prédéfinis comme hyperparamètres ou appris comme paramètres. Mathématiquement, la transformation du codeur s'exprime comme suit :
De la deuxième hypothèse, on sait que la distribution de chaque variable latente dans l'encodeur est divisée par le précédent La variable latente de couche est une distribution gaussienne centrée. Contrairement à MHVAE, la structure du codeur à chaque pas de temps n'est pas apprise, elle est fixée comme un modèle gaussien linéaire, où la moyenne et l'écart type peuvent être prédéfinis comme hyperparamètres ou appris comme paramètres. Mathématiquement, la transformation du codeur s'exprime comme suit :
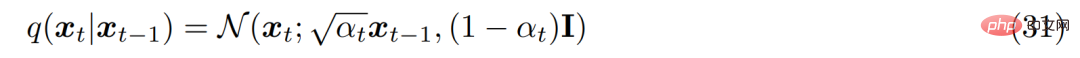 Pour la troisième hypothèse, α_t évolue dans le temps selon un planning fixe ou apprenable, tel que la distribution de la variable latente finale p(x_T) est la distribution gaussienne standard. La distribution conjointe de MHVAE peut alors être mise à jour et la distribution conjointe de VDM peut s'écrire comme suit :
Pour la troisième hypothèse, α_t évolue dans le temps selon un planning fixe ou apprenable, tel que la distribution de la variable latente finale p(x_T) est la distribution gaussienne standard. La distribution conjointe de MHVAE peut alors être mise à jour et la distribution conjointe de VDM peut s'écrire comme suit :
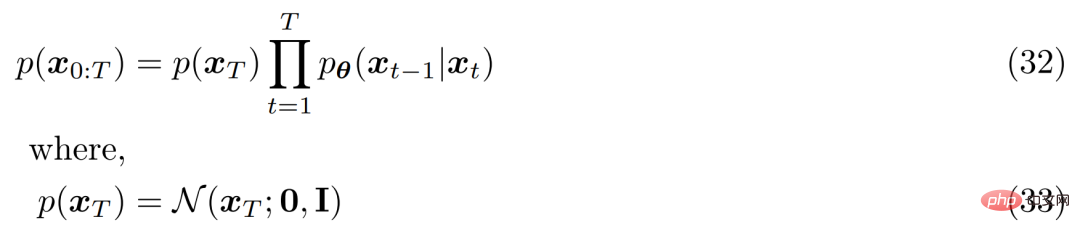 En résumé, cette série d'hypothèses décrit le bruit stable d'une image évoluant dans le temps. Les chercheurs ont progressivement corrompu l’image en ajoutant du bruit gaussien jusqu’à ce qu’elle devienne finalement identique au bruit gaussien.
En résumé, cette série d'hypothèses décrit le bruit stable d'une image évoluant dans le temps. Les chercheurs ont progressivement corrompu l’image en ajoutant du bruit gaussien jusqu’à ce qu’elle devienne finalement identique au bruit gaussien.
Semblable à n'importe quel HVACE, le VDM peut être optimisé en maximisant la limite inférieure des preuves (ELBO), qui peut être dérivée comme suit :
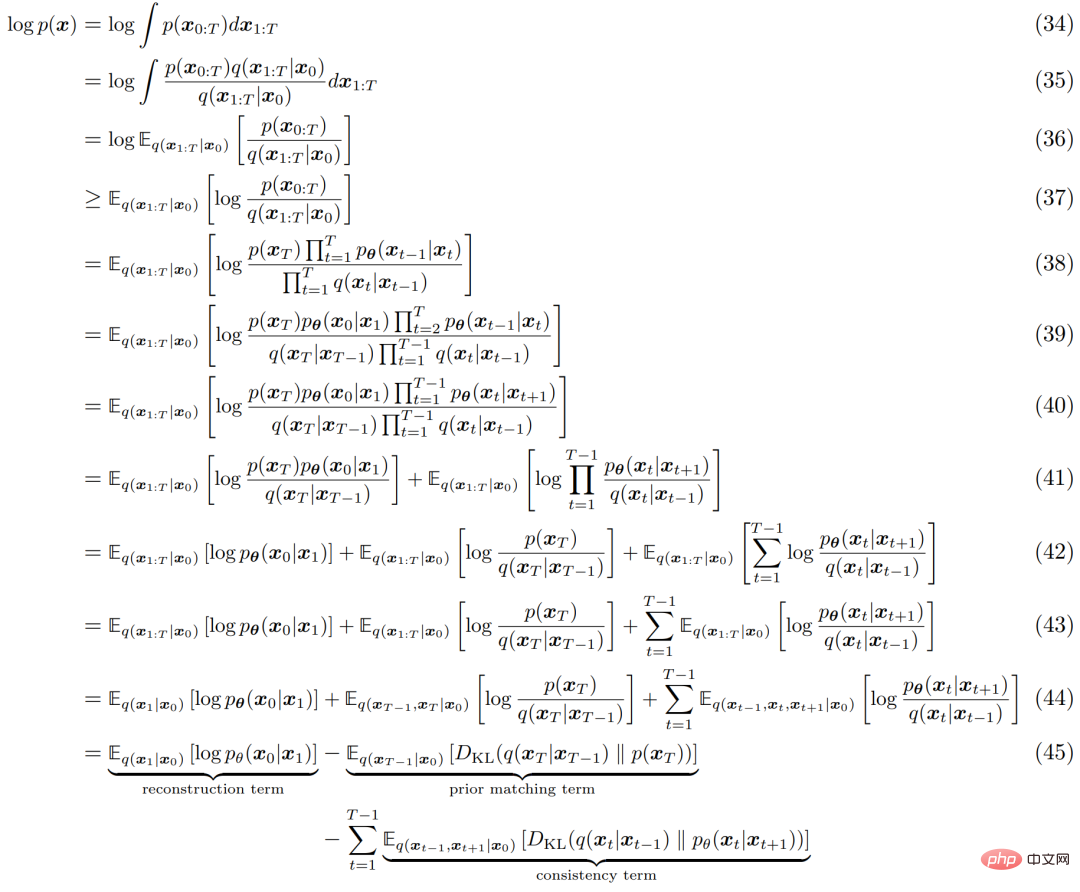 Le processus d'interprétation de l'ELBO est illustré dans la figure 4 ci-dessous. . :
Le processus d'interprétation de l'ELBO est illustré dans la figure 4 ci-dessous. . :
Trois interprétations équivalentes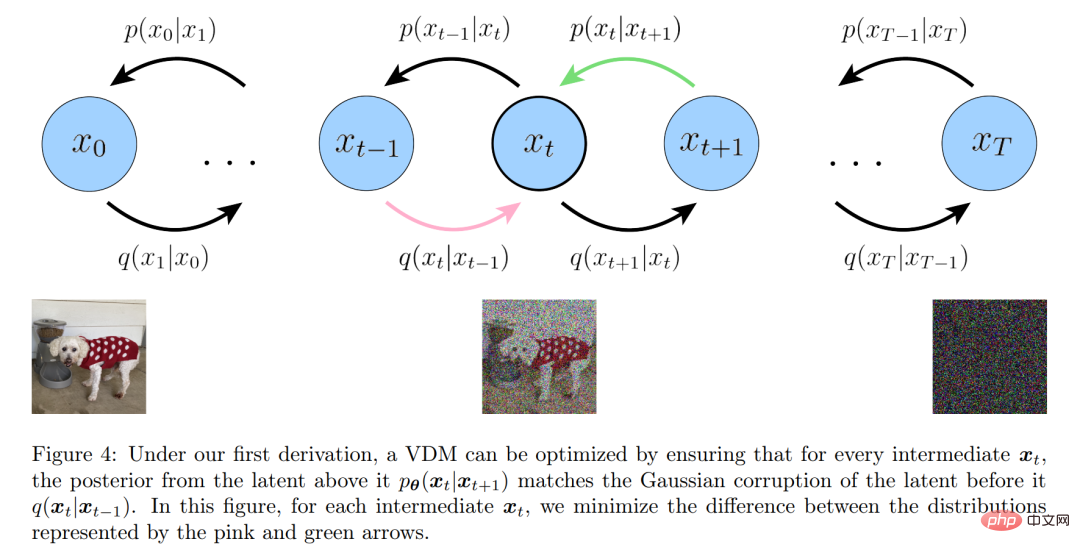
Tout d'abord, vous pouvez utiliser la technique de paramétrage lourd. Lors de la dérivation de la forme de q(x_t|x_0), l'équation 69 peut être réorganisée comme suit :
En l'introduisant dans la véritable moyenne de transformation de débruitage µ_q(x_t, x_0) précédemment dérivée, elle peut être re-dérivée comme suit : 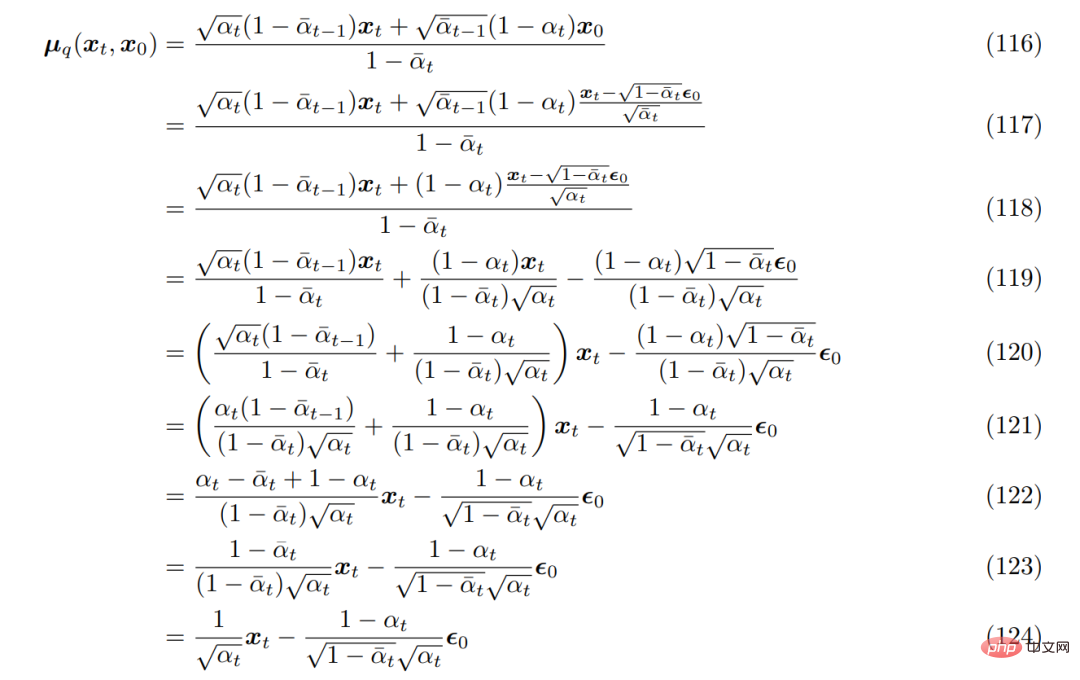
Par conséquent, la moyenne approximative de transformation de débruitage µ_θ(x_t, t) peut être définie comme suit :
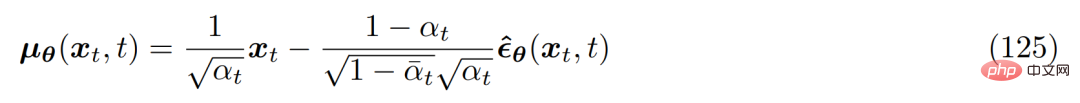
et le problème d'optimisation correspondant devient le suivant :
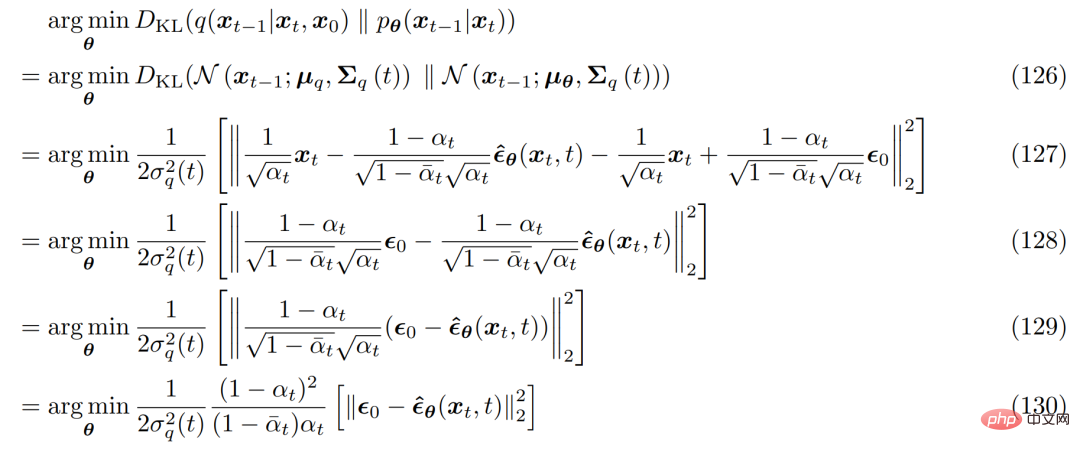
Afin de dériver les trois interprétations courantes des modèles de diffusion variationnelle, il faut se tourner vers la formule de Tweedie, ce qui fait référence au fait que lorsqu'un échantillon est donné, la vraie moyenne d'une distribution familiale exponentielle peut être estimée par l'estimation du maximum de vraisemblance de l'échantillon (également appelée moyenne empirique) plus un terme de correction impliquant le score estimé.
Mathématiquement parlant, pour une variable gaussienne z ∼ N (z; µ_z, Σ_z), la formule de Tweedie s'exprime comme suit :
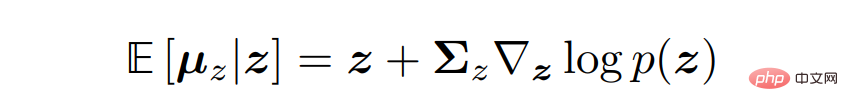
Modèle génératif basé sur les scores
Des chercheurs ont montré que , Les modèles de diffusion variationnelle peuvent être appris simplement en optimisant un réseau neuronal s_θ(x_t, t) pour prédire une fonction de score ∇ log p(x_t). Cependant, le terme de notation dans la dérivation provient de l'application de la formule de Tweedie. Cela ne fournit pas nécessairement une bonne intuition ou un bon aperçu de ce qu’est exactement la fonction de score ou pourquoi elle mérite d’être modélisée.
Heureusement, nous pouvons obtenir cette intuition à l'aide d'un autre type de modèle génératif, à savoir le modèle génératif basé sur les scores. Les chercheurs ont en effet démontré que la formulation VDM précédemment dérivée possède une formulation de modélisation générative basée sur des fractions équivalente, permettant une commutation flexible entre les deux interprétations.
Pour comprendre pourquoi l’optimisation d’une fonction de score est logique, les chercheurs ont revisité les modèles basés sur l’énergie. Une distribution de probabilité flexible arbitraire peut être écrite comme suit :

Une façon d'éviter de calculer ou de modéliser la constante de normalisation est d'utiliser un réseau neuronal s_θ(x) pour apprendre le score de la distribution p( x) Fonction ∇ log p(x). On observe que les deux côtés de l'équation 152 peuvent être différenciés logarithmiquement :
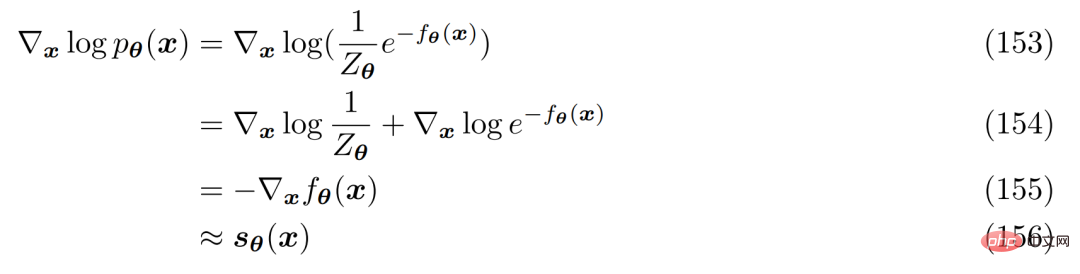
qui peut être librement exprimé comme un réseau neuronal sans impliquer de constantes de normalisation. La fonction de score peut être optimisée en minimisant la divergence de Fisher à l'aide de la fonction de score réel.

Intuitivement parlant, la fonction score définit un champ vectoriel sur tout l'espace où se trouvent les données x et pointe vers le modèle, comme le montre la figure 6 ci-dessous.
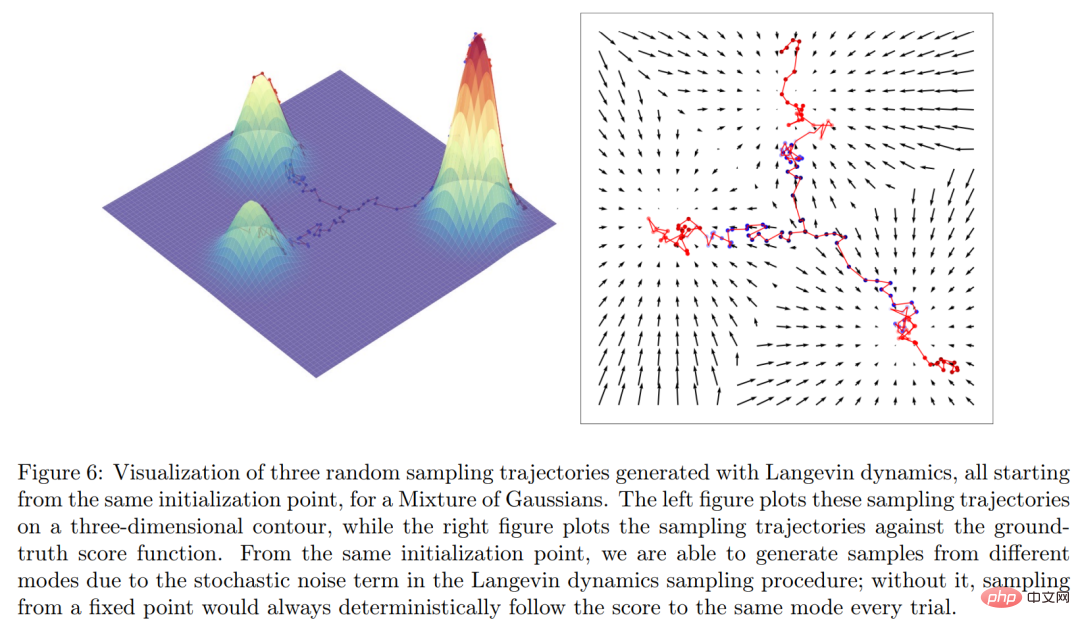
Enfin, les chercheurs ont établi un lien explicite entre le modèle de diffusion variationnelle et le modèle génératif basé sur les scores à partir des objectifs de formation et du processus d'échantillonnage.
Veuillez vous référer au document original pour plus de détails.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Imaginez un modèle d'intelligence artificielle qui non seulement a la capacité de surpasser l'informatique traditionnelle, mais qui permet également d'obtenir des performances plus efficaces à moindre coût. Ce n'est pas de la science-fiction, DeepSeek-V2[1], le modèle MoE open source le plus puissant au monde est ici. DeepSeek-V2 est un puissant mélange de modèle de langage d'experts (MoE) présentant les caractéristiques d'une formation économique et d'une inférence efficace. Il est constitué de 236B paramètres, dont 21B servent à activer chaque marqueur. Par rapport à DeepSeek67B, DeepSeek-V2 offre des performances plus élevées, tout en économisant 42,5 % des coûts de formation, en réduisant le cache KV de 93,3 % et en augmentant le débit de génération maximal à 5,76 fois. DeepSeek est une entreprise explorant l'intelligence artificielle générale
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L’IA change effectivement les mathématiques. Récemment, Tao Zhexuan, qui a prêté une attention particulière à cette question, a transmis le dernier numéro du « Bulletin de l'American Mathematical Society » (Bulletin de l'American Mathematical Society). En se concentrant sur le thème « Les machines changeront-elles les mathématiques ? », de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, intense et passionnant. L'auteur dispose d'une équipe solide, comprenant Akshay Venkatesh, lauréat de la médaille Fields, le mathématicien chinois Zheng Lejun, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur. Le monde de l’IA a radicalement changé. Vous savez, bon nombre de ces articles ont été soumis il y a un an.
 Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Les performances de JAX, promu par Google, ont dépassé celles de Pytorch et TensorFlow lors de récents tests de référence, se classant au premier rang sur 7 indicateurs. Et le test n’a pas été fait sur le TPU présentant les meilleures performances JAX. Bien que parmi les développeurs, Pytorch soit toujours plus populaire que Tensorflow. Mais à l’avenir, des modèles plus volumineux seront peut-être formés et exécutés sur la base de la plate-forme JAX. Modèles Récemment, l'équipe Keras a comparé trois backends (TensorFlow, JAX, PyTorch) avec l'implémentation native de PyTorch et Keras2 avec TensorFlow. Premièrement, ils sélectionnent un ensemble de
 Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas entre officiellement dans l’ère des robots électriques ! Hier, l'Atlas hydraulique s'est retiré "en larmes" de la scène de l'histoire. Aujourd'hui, Boston Dynamics a annoncé que l'Atlas électrique était au travail. Il semble que dans le domaine des robots humanoïdes commerciaux, Boston Dynamics soit déterminé à concurrencer Tesla. Après la sortie de la nouvelle vidéo, elle a déjà été visionnée par plus d’un million de personnes en seulement dix heures. Les personnes âgées partent et de nouveaux rôles apparaissent. C'est une nécessité historique. Il ne fait aucun doute que cette année est l’année explosive des robots humanoïdes. Les internautes ont commenté : Les progrès des robots ont fait ressembler la cérémonie d'ouverture de cette année à des êtres humains, et le degré de liberté est bien plus grand que celui des humains. Mais n'est-ce vraiment pas un film d'horreur ? Au début de la vidéo, Atlas est allongé calmement sur le sol, apparemment sur le dos. Ce qui suit est à couper le souffle
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
La dernière vidéo du robot Optimus de Tesla est sortie, et il peut déjà fonctionner en usine. À vitesse normale, il trie les batteries (les batteries 4680 de Tesla) comme ceci : Le responsable a également publié à quoi cela ressemble à une vitesse 20 fois supérieure - sur un petit "poste de travail", en sélectionnant et en sélectionnant et en sélectionnant : Cette fois, il est publié L'un des points forts de la vidéo est qu'Optimus réalise ce travail en usine, de manière totalement autonome, sans intervention humaine tout au long du processus. Et du point de vue d'Optimus, il peut également récupérer et placer la batterie tordue, en se concentrant sur la correction automatique des erreurs : concernant la main d'Optimus, le scientifique de NVIDIA Jim Fan a donné une évaluation élevée : la main d'Optimus est l'un des robots à cinq doigts du monde. le plus adroit. Ses mains ne sont pas seulement tactiles
 FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
La détection de cibles est un problème relativement mature dans les systèmes de conduite autonome, parmi lesquels la détection des piétons est l'un des premiers algorithmes à être déployés. Des recherches très complètes ont été menées dans la plupart des articles. Cependant, la perception de la distance à l’aide de caméras fisheye pour une vue panoramique est relativement moins étudiée. En raison de la distorsion radiale importante, la représentation standard du cadre de délimitation est difficile à mettre en œuvre dans les caméras fisheye. Pour alléger la description ci-dessus, nous explorons les conceptions étendues de boîtes englobantes, d'ellipses et de polygones généraux dans des représentations polaires/angulaires et définissons une métrique de segmentation d'instance mIOU pour analyser ces représentations. Le modèle fisheyeDetNet proposé avec une forme polygonale surpasse les autres modèles et atteint simultanément 49,5 % de mAP sur l'ensemble de données de la caméra fisheye Valeo pour la conduite autonome.
 DualBEV : dépassant largement BEVFormer et BEVDet4D, ouvrez le livre !
Mar 21, 2024 pm 05:21 PM
DualBEV : dépassant largement BEVFormer et BEVDet4D, ouvrez le livre !
Mar 21, 2024 pm 05:21 PM
Cet article explore le problème de la détection précise d'objets sous différents angles de vue (tels que la perspective et la vue à vol d'oiseau) dans la conduite autonome, en particulier comment transformer efficacement les caractéristiques de l'espace en perspective (PV) en vue à vol d'oiseau (BEV). implémenté via le module Visual Transformation (VT). Les méthodes existantes sont globalement divisées en deux stratégies : la conversion 2D en 3D et la conversion 3D en 2D. Les méthodes 2D vers 3D améliorent les caractéristiques 2D denses en prédisant les probabilités de profondeur, mais l'incertitude inhérente aux prévisions de profondeur, en particulier dans les régions éloignées, peut introduire des inexactitudes. Alors que les méthodes 3D vers 2D utilisent généralement des requêtes 3D pour échantillonner des fonctionnalités 2D et apprendre les poids d'attention de la correspondance entre les fonctionnalités 3D et 2D via un transformateur, ce qui augmente le temps de calcul et de déploiement.





