
「Dans un graphe orienté pondéré G=(V,E), le poids de chaque arête est un nombre réel De plus, un sommet en V est également donné, appelé la source.
Calcul du. La longueur du chemin le plus court entre la source et tous les autres sommets est le problème du chemin le plus court à source unique (SSSP). Les chercheurs du monde entier travaillent dur pour résoudre ce problème depuis plus d'un demi-siècle. Aujourd’hui, ce casse-tête algorithmique a finalement été résolu avec succès par une équipe de recherche du Département d’informatique de l’Université de Copenhague.
Algorithme SSSP de poids négatif : rapide et efficace
Lien papier : https://arxiv.org/abs/2203.03456
Dans une interview, le chercheur Christian Wulff -Nilsen a déclaré que leur solution est le premier algorithme de combinaison SSSP avec des poids négatifs à briser la contrainte de temps de fonctionnement Õ(
n(4/3) log W) qui existe depuis plus de 30 ans. Il existe deux algorithmes classiques concernant SSSP : l'algorithme de Dijkstra (algorithme de Dijkstra) et l'algorithme de Bellman-Ford (algorithme de Bellman-Ford), qui ont tous deux leurs propres limites.
L'algorithme de Dijkstra a le temps de fonctionnement le plus court et peut atteindre un temps presque linéaire O(
m+ n log n), mais il ne peut pas calculer les bords de poids négatifs. L'algorithme Bellman-Ford peut calculer des bords de poids négatifs, mais le temps de fonctionnement est trop long, atteignant O(
mn). Actuellement, les algorithmes SSSP de pointe pour résoudre les arêtes à pondération négative reposent sur une optimisation continue complexe et des algorithmes algébriques et graphiques dynamiques. Cela conduit au fait que même si les générations ultérieures de chercheurs continuent d'optimiser l'algorithme, son temps de calcul nécessite toujours Õ(n(4/3) log W). Cette contrainte de temps de calcul existe depuis trente ans. Face à ces limitations, Wulff-Nilsen a soulevé deux questions :
1) Le fonctionnement de l'algorithme de bord à pondération négative peut-il atteindre un temps quasi-linéaire ?
2) Cela peut-il être réalisé avec des outils simples ?
Existe-t-il une méthode qui demande à la fois du temps et de la qualité ?
Ne le dites pas, ça existe vraiment.
L'algorithme proposé par Wulff-Nilsen est un algorithme de mise à l'échelle d'image, qui est amélioré par l'algorithme simple de décomposition d'image Low Diameter Decomposition. Habituellement, cet algorithme de décomposition n'est utilisé que pour la décomposition graphique d'arêtes à pondération non négative, et l'une des contributions de cette recherche est de l'appliquer aux images d'arêtes à pondération négative pour renforcer l'algorithme de mise à l'échelle récursive SSSP à arêtes à pondération négative.
Le processus de dérivationWulff-Nilsen est basé sur l'algorithme de prix de Johnson. Proposer : Dans l'image
G= (
V, E, w), soit Φ n'importe quelle fonction : V→Z. Soit w(Φ) la fonction de poids : définition : , : . Dans l'image G = (V, E,w) et l'image G' = (V, E,w'), si : 1) Image La distance la plus courte dans G est égale à la distance la plus courte dans l'image G', et vice versa ; 2) G ne contient que des anneaux de poids négatif lorsque G' contient un poids négatif anneaux, Alors l'image G est égale à l'image G'. Corollaire 2.7 Considérons une image arbitraire Le but de cet algorithme est de rendre tous les poids de bord dans GΦ non négatifs lors du calcul de la fonction de prix Φ, en supposant qu'il n'y a pas de cycle de poids négatif. Ensuite, vous pouvez exécuter l'algorithme de Dijkstra sur Après cela, Wulff-Nilsen a commencé à présenter son cadre algorithmique. Premièrement, Wulff-Nilsen suppose qu'il existe un algorithme Dijkstra (G,s), saisissant un graphe G sans arêtes de poids négatifs, sommets s∈ V, G dans s génère l’arborescence du chemin le plus court. La durée d'exécution est de O(m + n log n). Si G est un DAG (graphe acyclique dirigé), calculer une fonction de prix Φ telle que Le but du problème du chemin le plus court à source unique est de trouver le chemin le plus court entre un nœud de départ donné et tous les autres nœuds du réseau. Un réseau est représenté comme un graphe composé de nœuds et des connexions entre eux, appelées arêtes. Chaque bord a une direction (par exemple, cela peut être utilisé pour représenter une route à sens unique) et un poids qui représente le coût du déplacement le long de ce bord. Si tous les poids des bords sont non négatifs, le problème peut être résolu en un temps presque linéaire en utilisant l'algorithme classique de Dijkstra. Les nouveaux résultats résolvent ce problème presque en même temps que l'algorithme de Dijkstra, mais permettent également des poids de bord négatifs. Après , Wulff-Nilsen a mentionné les deux algorithmes les plus importants dans les outils combinés : ScaleDown et SPmain. L'algorithme ScaleDown s'exécute par étapes, et dans la dernière étape, il utilise ElimNeg( Cela signifie que, pour tous Si l'algorithme se termine, alors pour tout Cela signifie pour tous Par induction, en supposant que la théorie est valable pour Par conséquent, grâce à la sortie de Parce que Nous pouvons donc conclure que si Cela peut prouver l'exactitude de l'algorithme SPmain. À ce stade, les deux algorithmes les plus importants de la solution SSSP à poids négatif de Wulff-Nilsen se sont avérés vrais. Le nouvel algorithme introduit avec succès des poids négatifs tout en garantissant un temps quasi-linéaire. L'année dernière, Wulff-Nilsen a fait une autre percée dans le même domaine, impliquant comment trouver le chemin le plus court dans un réseau qui change avec le temps. Sa solution à une énigme récente s’appuie sur ce travail. Il pense que la résolution du problème SSSP peut ouvrir la voie à des algorithmes qui peuvent non seulement aider les véhicules électriques à calculer instantanément l'itinéraire le plus rapide vers leur destination, mais également garantir qu'ils le font de la manière la plus économe en énergie. Wulff-Nilsen a expliqué : « Notre algorithme ajoute un poids négatif, une dimension que les algorithmes précédents n'avaient pas. Un exemple pratique est que lors de la conduite en montagne, avec la dimension de poids négatif, le système de navigation peut recommander des itinéraires avec. de nombreuses routes de descente pour les propriétaires de véhicules électriques afin que les véhicules électriques puissent se recharger en descente » Wulff-Nilsen a également déclaré que leur algorithme peut non seulement être utilisé pour la planification d'itinéraires de véhicules électriques, mais aussi pour la surveillance des spéculations. le secteur financier. Il a déclaré : « En principe, cet algorithme peut être utilisé pour fournir une alerte précoce aux utilisateurs tels que les banques centrales, avertissant les spéculateurs spéculant sur l'achat et la vente de diverses devises. Aujourd'hui, de nombreux criminels utilisent des ordinateurs pour commettre des crimes, mais parce que notre algorithme est si vite, cela peut être possible. Il est utilisé pour surveiller et détecter les vulnérabilités à temps avant que les gens ne les exploitent. « En 1959, lorsque Dijkstra a proposé pour la première fois le problème de la distance la plus courte, il n'aurait probablement pas pensé que les gens optimisaient continuellement ce problème. plan de plus de 60 ans. Vous pourriez également être surpris que la réponse à l’énigme ait des connotations si riches. C'est peut-être ça le charme de la science. 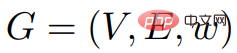 et une fonction prix Φ. En toi, v ∈ V,
et une fonction prix Φ. En toi, v ∈ V, 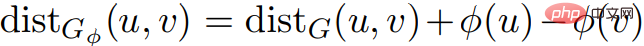 . Et dans n'importe quelle bague C,
. Et dans n'importe quelle bague C, 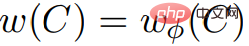 . Par conséquent, G et
. Par conséquent, G et 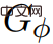 sont égaux. Si
sont égaux. Si 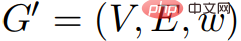
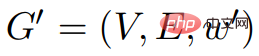 ,
,  , alors G et G' sont égaux.
, alors G et G' sont égaux. 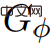 .
. 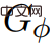 ait des bords de poids non négatifs est simple : juste v1, ... , bouclez sur vn et définissez Φ(vi) pour que tous les poids de bord entrants soient non négatifs.
ait des bords de poids non négatifs est simple : juste v1, ... , bouclez sur vn et définissez Φ(vi) pour que tous les poids de bord entrants soient non négatifs. 
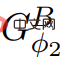 ) pour calculer la fonction de prix Φ2. Si ElimNeg se termine, il renverra la fonction de prix ψ′, rendant
) pour calculer la fonction de prix Φ2. Si ElimNeg se termine, il renverra la fonction de prix ψ′, rendant 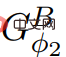 toutes les valeurs de bord non négatives, en d'autres termes, car
toutes les valeurs de bord non négatives, en d'autres termes, car 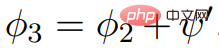 , donc
, donc 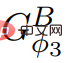 ne contient pas ; poids négatifs.
ne contient pas ; poids négatifs. 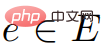 ,
, 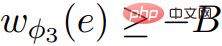 satisfait à la condition (car
satisfait à la condition (car 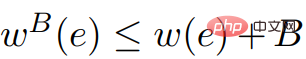 ). Cela prouve l'exactitude de la sortie ScaleDown.
). Cela prouve l'exactitude de la sortie ScaleDown. 
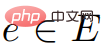 et
et 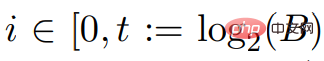 ,
, 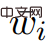 est l'intégrale, et pour tout
est l'intégrale, et pour tout 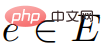 ,
, 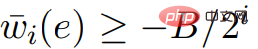 .
. 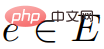 ,
, 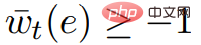 . Par conséquent, le graphique G* a des poids non négatifs.
. Par conséquent, le graphique G* a des poids non négatifs. 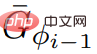 , l'appel à ScaleDown
, l'appel à ScaleDown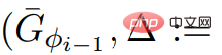
 à la ligne 5 de l'algorithme satisfait les propriétés d'entrée nécessaires.
à la ligne 5 de l'algorithme satisfait les propriétés d'entrée nécessaires. 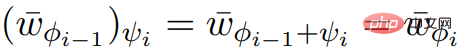 et ScaleDown, vous pouvez obtenir
et ScaleDown, vous pouvez obtenir 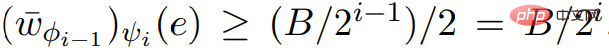 .
. 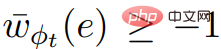 , Si C est un poids négatif sonne dans
, Si C est un poids négatif sonne dans  , puisque toutes les valeurs de dans
, puisque toutes les valeurs de dans  sont des multiples de 2n, et
sont des multiples de 2n, et 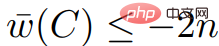 ; Nous savons également que
; Nous savons également que 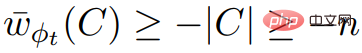 , , donc
, , donc 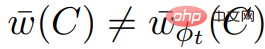 est incompatible avec le corollaire 2.7.
est incompatible avec le corollaire 2.7. 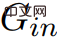 contient un cycle de poids négatif, l'algorithme ne se terminera pas.
contient un cycle de poids négatif, l'algorithme ne se terminera pas. 60 ans plus tard, la recherche de réponses est plus qu'un simple casse-tête
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Algorithme de remplacement de page
Algorithme de remplacement de page
 Utilisation de PathFileExists
Utilisation de PathFileExists
 Comment utiliser la fonction nanosleep
Comment utiliser la fonction nanosleep
 Quelle plateforme est Fengxiangjia ?
Quelle plateforme est Fengxiangjia ?
 métamoteur de recherche
métamoteur de recherche
 Méthodes d'analyse des données
Méthodes d'analyse des données
 Comment résoudre le problème selon lequel WLAN n'a pas de configuration IP valide
Comment résoudre le problème selon lequel WLAN n'a pas de configuration IP valide
 Outils de test de logiciels
Outils de test de logiciels
 La différence entre le lecteur C et le lecteur D
La différence entre le lecteur C et le lecteur D