
Depuis que Google a proposé Vision Transformer (ViT), ViT est progressivement devenu l'épine dorsale par défaut de nombreuses tâches visuelles. Avec la structure ViT, le SoTA pour de nombreuses tâches visuelles a été encore amélioré, notamment la classification, la segmentation, la détection, la reconnaissance, etc.
Cependant, former ViT n’est pas chose aisée. En plus de nécessiter des techniques de formation plus complexes, la quantité de calcul requise pour la formation du modèle est souvent bien supérieure à celle des CNN précédents. Récemment, les équipes de recherche du Singapore Sea AI LAB (SAIL) et du ZERO Lab de l'Université de Pékin ont proposé conjointement un nouveau optimiseur de modèle profond Adan, qui peut compléter la formation de ViT avec seulement la moitié du montant de calcul.

Lien papier : https://arxiv.org/pdf/2208.06677.pdf
Lien code : https://github.com/sail-sg/Adan
De plus, avec la même quantité de calcul, Adan peut effectuer dans plusieurs scénarios (impliquant CV, PNL, RL), plusieurs méthodes de formation (supervisées et auto-supervisées) et diverses structures/algorithmes de réseau( Swin, ViT, ResNet, ConvNext, MAE, LSTM, BERT, Transformer-XL, algorithme PPO), tous ont obtenu des améliorations de performances.
Le code, les fichiers de configuration et les journaux de formation sont tous open source.
Paradigme de formation et optimiseur de modèles profondsAvec l'introduction de ViT, les méthodes de formation des modèles profonds sont devenues de plus en plus complexes. Les techniques de formation courantes incluent l'amélioration des données complexes (telles que MixUp, CutMix, AutoRand), le traitement des étiquettes (telles que le lissage des étiquettes et l'étiquette de bruit), la moyenne mobile des paramètres du modèle, la profondeur du réseau aléatoire, l'abandon, etc. Avec l'application mixte de ces techniques, la généralisation et la robustesse du modèle ont été améliorées, mais parallèlement, la complexité informatique de la formation du modèle est devenue de plus en plus grande.
Sur ImageNet 1k, le nombre d'époques de formation est passé de 90 récemment proposées par ResNet à 300 couramment utilisées pour la formation ViT. Même pour certains modèles d'apprentissage auto-supervisés, tels que MAE et ViT, le nombre d'époques de pré-formation a atteint 1,6 000. L'augmentation du temps de formation signifie que la durée de la formation est considérablement allongée, ce qui augmente fortement le coût de la recherche universitaire ou de la mise en œuvre industrielle. Une solution courante à l'heure actuelle consiste à augmenter la taille du lot de formation et à faciliter la formation en parallèle pour réduire le temps de formation. Cependant, le problème qui l'accompagne est qu'une taille de lot importante signifie souvent une diminution des performances, et plus la taille du lot est grande, plus elle est évidente. la situation.
Cela est principalement dû au fait que le nombre de mises à jour des paramètres du modèle diminue fortement à mesure que la taille du lot augmente. L'optimiseur actuel ne peut pas réaliser une formation rapide du modèle avec un petit nombre de mises à jour dans des paradigmes de formation complexes, ce qui aggrave encore l'augmentation du nombre d'époques de formation du modèle.
Alors, existe-t-il un nouvel optimiseur capable d'entraîner des modèles approfondis plus rapidement et mieux avec moins de mises à jour de paramètres ? Tout en réduisant le nombre d’époques de formation, cela peut-il également atténuer l’impact négatif de l’augmentation de la taille des lots ?
Impulsion ignoréePour accélérer la vitesse de convergence de l'optimiseur, le moyen le plus direct est d'introduire une impulsion. Les optimiseurs de modèles profonds proposés ces dernières années suivent tous le paradigme d'impulsion utilisé dans Adam - la méthode de la balle lourde :
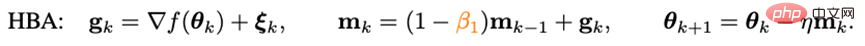
où g_k est le bruit aléatoire, m_k est le moment et eta est le taux d'apprentissage. Adam a modifié la mise à jour de m_k de la forme cumulative à la forme de moyenne mobile et a introduit le moment de second ordre (n_k) pour augmenter le taux d'apprentissage, à savoir :
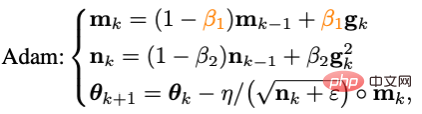
Cependant, comme Adam n'a pas réussi à entraîner le ViT original, sa version améliorée AdamW est progressivement devenue le premier choix pour entraîner ViT et même ConvNext. Cependant, AdamW ne change pas le paradigme d'impulsion chez Adam, donc lorsque la taille du lot dépasse 4 096, les performances de ViT entraînées par AdamW chuteront fortement.
Dans le domaine de l'optimisation convexe traditionnelle, il existe une technique d'impulsion aussi célèbre que la méthode de la balle lourde - Algorithme d'impulsion Nesterov :
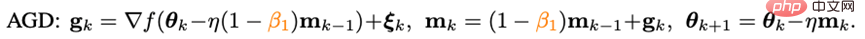
L'algorithme d'impulsion Nesterov a de bonnes performances sur des surfaces lisses. et des problèmes généralement convexes. Il a une vitesse de convergence théorique plus rapide que la méthode des billes lourdes et peut théoriquement supporter des lots de plus grande taille. Différent de la méthode de la balle pondérée, l'algorithme Nesterov ne calcule pas le gradient au point actuel, mais utilise l'impulsion pour trouver un point d'extrapolation, puis accumule l'impulsion après avoir calculé le gradient à ce point.
Les points d'extrapolation peuvent aider l'algorithme Nesterov à percevoir à l'avance les informations géométriques autour du point actuel. Cette caractéristique rend l'impulsion de Nesterov plus adaptée aux paradigmes de formation complexes et aux structures de modèle (telles que ViT), car elle ne s'appuie pas simplement sur les impulsions passées pour contourner les points minimums locaux précis, mais les ajuste en observant à l'avance les gradients environnants.
Bien que l'algorithme d'impulsion de Nesterov présente certains avantages, il a rarement été appliqué et exploré dans les optimiseurs approfondis. L'une des principales raisons est que l'algorithme de Nesterov doit calculer le gradient au point d'extrapolation et le mettre à jour au point actuel. Pendant cette période, il nécessite plusieurs rechargements de paramètres de modèle et une rétro-propagation artificielle (BP) au point d'extrapolation. Ces inconvénients limitent considérablement l'application de l'algorithme d'impulsion de Nesterov dans les optimiseurs de modèles profonds.
En combinant l'impulsion Nesterov réécrite avec l'algorithme d'optimisation adaptative et en introduisant une décroissance de poids découplée, l'optimiseur Adan final peut être obtenu. À l'aide de points d'extrapolation, Adan peut percevoir à l'avance les informations sur le gradient environnant, s'échappant ainsi efficacement des zones minimales locales précises pour accroître la généralisation du modèle.
1) Impulsion adaptative de Nesterov
Afin de résoudre le problème de la surcharge de plusieurs paramètres de modèle dans l'algorithme d'impulsion de Nesterov, les chercheurs ont d'abord réécrit Nesterov :
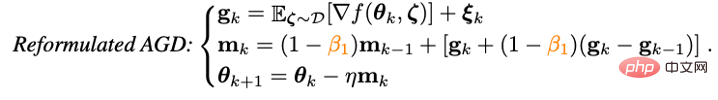
On peut prouver que , L'algorithme d'impulsion Nesterov réécrit est équivalent à l'algorithme original. Les points d'itération des deux peuvent être convertis l'un dans l'autre et les points de convergence finaux sont les mêmes. On peut voir qu’en introduisant le terme différentiel du gradient, la surcharge manuelle des paramètres et la pression artérielle artificielle au point d’extrapolation peuvent être évitées.
Combinez l'algorithme d'impulsion Nesterov réécrit avec l'optimiseur de classe adaptatif - remplacez la mise à jour de m_k de la forme cumulative à la forme moyenne mobile et utilisez le moment de second ordre pour augmenter le taux d'apprentissage :
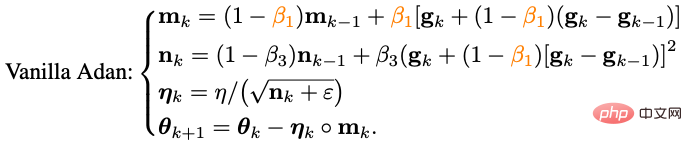
Nous avons maintenant obtenu la version de base de l'algorithme d'Adan.
2) Impulsion de différence de dégradé
On peut constater que la mise à jour de m_k couple le dégradé et la différence de dégradé ensemble, mais dans les scénarios réels, il est souvent nécessaire de traiter les deux éléments avec différentes significations physiques séparément, les chercheurs ont donc introduit l'impulsion v_k de la différence de gradient :
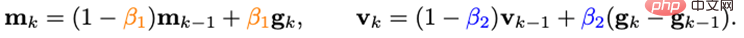
Ici, différents coefficients d'impulsion/moyenne sont définis pour l'impulsion du gradient et l'impulsion de sa différence. Le terme de différence de gradient peut ralentir la mise à jour de l'optimiseur lorsque les dégradés adjacents sont incohérents, et inversement, accélérer la mise à jour lorsque les directions des gradients sont cohérentes.
3) Décroissance pondérale découplée
Pour la fonction objectif avec régularisation du poids L2, l'optimiseur AdamW actuellement populaire a obtenu de meilleures performances sur ViT et ConvNext en découplant la régularisation L2 et la perte d'entraînement. Cependant, la méthode de découplage utilisée par AdamW est biaisée en faveur de l’heuristique, et il n’existe actuellement aucune garantie théorique de sa convergence.
Basée sur l'idée de découplage de la régularité L2, une stratégie de perte de poids découplée est également introduite dans Adan. À l'heure actuelle, chaque itération d'Adan peut être considérée comme minimisant une approximation du premier ordre de l'objectif d'optimisation F :
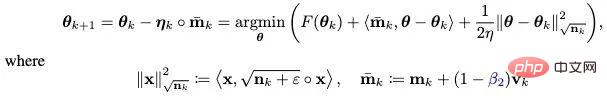
Étant donné que la régularisation du poids L2 dans F est trop simple et fluide, il n'est pas nécessaire de le faire. une approximation du premier ordre. Par conséquent, vous ne pouvez faire qu'une approximation de premier ordre de la perte d'entraînement et ignorer la régularité du poids L2, alors la dernière itération d'Adan deviendra :
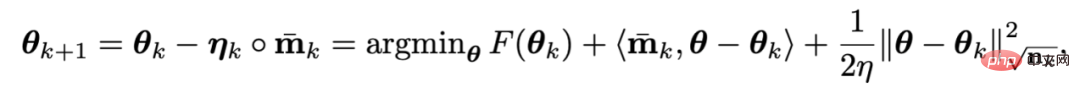
Fait intéressant, on peut constater que le critère de mise à jour d'AdamW est le critère de mise à jour d'Adan dans une approximation du premier ordre lorsque le taux d'apprentissage eta est proche de 0. Par conséquent, une explication raisonnable peut être donnée à Adan ou même à AdamW du point de vue de l’opérateur proximal au lieu de l’amélioration heuristique originale.
4) Optimiseur Adan
Combinez les deux améliorations 2) et 3) dans la version de base d'Adan, et vous pourrez obtenir l'optimiseur Adan suivant.

Adan combine les avantages de l'optimiseur adaptatif, de l'impulsion Nesterov et de la stratégie de décroissance du poids découplée, peut supporter des taux d'apprentissage et des tailles de lots plus élevés, et peut mettre en œuvre une régularisation dynamique L2 des paramètres du modèle.
5) Analyse de convergence
Ignorez ici le processus d'analyse mathématique compliqué et donnez seulement la conclusion :
Théorème : Deux types de conditions lisses de Hesse données ou non Dans de telles circonstances, le la vitesse de convergence de l'optimiseur Adan peut atteindre la limite inférieure théorique connue sur les problèmes d'optimisation stochastique non convexes, et cette conclusion est toujours vraie avec une stratégie de désintégration de poids découplée.
1) Apprentissage supervisé - Modèle ViT
Pour le modèle ViT, les chercheurs l'ont testé respectivement sur les structures ViT et Swin. performance.

On constate que par exemple, sur ViT-small, ViT-base, Swin-tiny et Swin-base, Adan ne consomme que la moitié des ressources informatiques pour obtenir des résultats proches de l'optimiseur SoTA, et Sous le même montant de calcul, Adan présente de grands avantages sur les deux modèles ViT.
De plus, les performances d'Adan ont également été testées sous de grandes tailles de lots :

On peut voir qu'Adan fonctionne bien sous différentes tailles de lots et est relativement conçu pour de grandes tailles de lots. L'optimiseur ( LAMB) présente également certains avantages.
2) Apprentissage supervisé - Modèle CNN
En plus du modèle ViT plus difficile à former, les chercheurs ont également testé les performances d'Adan sur des modèles CNN avec relativement peu de points minimum locaux précis - y compris le ResNet classique et le ConvNext plus avancé. Les résultats sont les suivants :
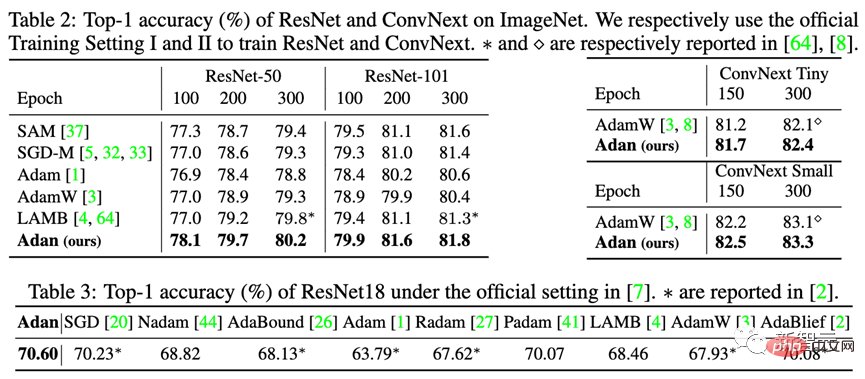
On peut observer que qu'il s'agisse de ResNet ou de ConvNext, Adan peut atteindre des performances au-delà de SoTA dans environ 2/3 de l'époque d'entraînement.
3) Apprentissage non supervisé
Dans le cadre de formation non supervisée, les chercheurs ont testé les performances d'Adan sur le MAE nouvellement proposé. Les résultats sont les suivants :

Conformément à la conclusion de l'apprentissage supervisé, Adan ne consomme que la moitié du montant de calcul pour égaler ou même dépasser l'optimiseur SoTA d'origine, et lorsque l'époque d'entraînement devient plus petite, l'avantage d'Adan devient plus grand. . Plus c’est évident.
1) Apprentissage supervisé
Sur la tâche d'apprentissage supervisé de la PNL, observez les performances d'Adan sur le LSTM classique et le Transformer-XL avancé.
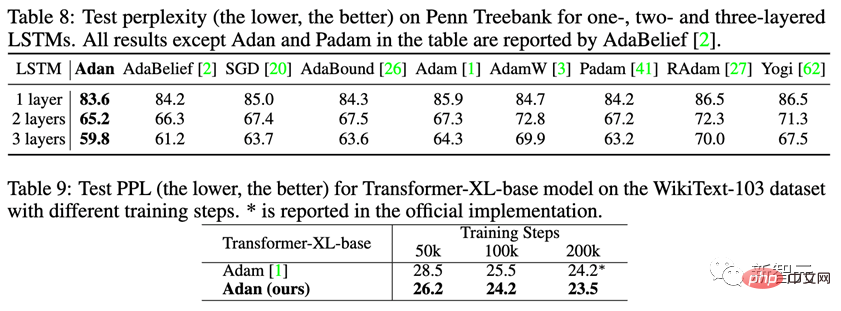
Adan a montré une supériorité constante sur les deux réseaux ci-dessus. Et pour Transformer-XL, Adan a lié l'optimiseur Adam par défaut en deux fois moins d'étapes de formation.
2) Apprentissage non supervisé
Afin de tester la formation modèle d'Adan sur des tâches non supervisées dans des scénarios PNL. Les chercheurs ont formé BERT à partir de zéro : après 1 000 000 itérations de pré-entraînement, les performances du modèle formé par Adan ont été testées sur 7 sous-tâches de l'ensemble de données GLUE, et les résultats sont les suivants :

Adan a bien performé sur les 7 testés Il montre de grands avantages dans les tâches de classification de mots et de phrases. Il convient de mentionner que les résultats du modèle de base BERT formé par Adan sur certaines sous-tâches (telles que RTE, CoLA et SST-2) ont même dépassé le modèle BERT-large formé par Adam.
Les chercheurs ont remplacé l'optimiseur de l'algorithme PPO couramment utilisé en RL par Adan et ont testé les performances d'Adan sur 4 jeux dans le moteur MuJoCo. Dans 4 jeux, l'algorithme PPO utilisant Adan comme optimiseur de réseau peut toujours obtenir des récompenses plus élevées.
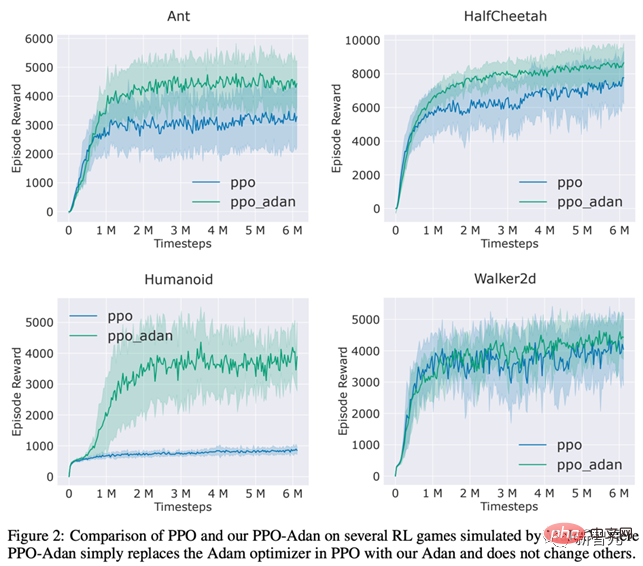
Adan montre également un grand potentiel en formation réseau RL.
L'optimiseur Adan introduit un nouveau paradigme d'impulsion aux optimiseurs de modèles profonds actuels. Réalisez une formation rapide de modèles selon des paradigmes de formation complexes avec moins de mises à jour.
Les expériences montrent que Adan peut égaler l'optimiseur SoTA existant avec seulement 1/2-2/3 du montant de calcul.
Adan a démontré des performances exceptionnelles dans plusieurs scénarios (impliquant CV, PNL, RL), plusieurs méthodes de formation (supervisées et auto-supervisées) et diverses structures de réseau (ViT, CNN, LSTM, Transformer, etc.) Gros avantage en termes de performances . De plus, la vitesse de convergence de l’optimiseur Adan a atteint la limite inférieure théorique de l’optimisation stochastique non convexe.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Quelle est la différence entre le protocole TCP et le protocole UDP ?
Quelle est la différence entre le protocole TCP et le protocole UDP ?
 comment créer un site Web
comment créer un site Web
 Comment intégrer des styles CSS dans HTML
Comment intégrer des styles CSS dans HTML
 WeChat Moments, deux tirets et un point
WeChat Moments, deux tirets et un point
 qu'est-ce que le framework vue
qu'est-ce que le framework vue
 Comment se connecter pour accéder à la base de données en VB
Comment se connecter pour accéder à la base de données en VB
 Moyenne du tableau
Moyenne du tableau
 Quelles sont les méthodes de détection des vulnérabilités ASP ?
Quelles sont les méthodes de détection des vulnérabilités ASP ?