 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Explication détaillée des méthodes de contrôle couramment utilisées pour la planification et le contrôle des voitures intelligentes
Explication détaillée des méthodes de contrôle couramment utilisées pour la planification et le contrôle des voitures intelligentes
Explication détaillée des méthodes de contrôle couramment utilisées pour la planification et le contrôle des voitures intelligentes
Le contrôle est la stratégie qui fait avancer le véhicule. L'objectif du contrôle est d'utiliser des quantités de contrôle réalisables pour minimiser les écarts par rapport à la trajectoire cible, maximiser le confort des passagers, etc.

Comme le montre la figure ci-dessus, les modules associés à l'entrée du module de contrôle comprennent le module de planification, le module de positionnement et les informations sur le véhicule, etc. Le module de positionnement fournit des informations de localisation du véhicule, le module de planification fournit des informations de trajectoire cible, et les informations sur le véhicule comprennent le rapport, la vitesse, l'accélération, etc. Les sorties de commande sont les grandeurs de direction, d'accélération et de freinage.
Le module de contrôle est principalement divisé en contrôle horizontal et contrôle vertical. Selon les différentes formes de couplage, il peut être divisé en deux méthodes : indépendante et intégrée.
1 Méthode de contrôle
1.1 Contrôle de découplage
Le contrôle dit de découplage signifie contrôler indépendamment les méthodes de contrôle horizontales et verticales.
1.2 Contrôle de couplage
Le contrôle de couplage prend en compte les problèmes de couplage qui existent en contrôle horizontal et vertical. Un exemple typique est qu'une voiture ne peut pas prendre un virage à grande vitesse car lorsque la vitesse longitudinale est trop élevée, la vitesse angulaire latérale doit être limitée, sinon la force centripète ne peut pas satisfaire l'accélération centripète.

La méthode représentative typique de l'intégration horizontale et verticale est le contrôle prédictif de modèle linéaire variable dans le temps. Cette méthode ajoute des contraintes conjointes horizontales et verticales sur la base du contrôle prédictif du modèle. Comme les contraintes d'accélération centripète maximale, etc.
1.3 Contrôle latéral

Comme le montre la figure ci-dessus, le contrôle latéral peut être divisé en méthodes géométriques, méthodes basées sur un modèle cinématique et méthodes basées sur un modèle dynamique.
1.3.1 Contrôle anticipatif
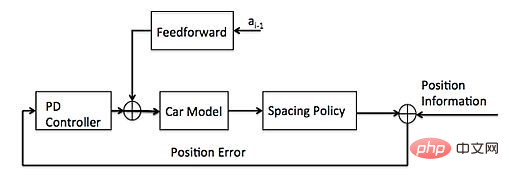
Le contrôle dit anticipatif signifie compenser de manière appropriée la quantité de contrôle à l'avance en fonction des informations du point de suivi. Un exemple typique consiste à utiliser les informations de courbure dans les points de la séquence de suivi pour compenser l'angle de rotation.
1.3.2 Forme chaînée
Le système chaîné effectue une linéarisation multicouche du système non linéaire. Il décompose le système couche par couche et peut accélérer le système, de la même manière que le système de filtrage [3].

Le modèle du système en coordonnées Frenet :
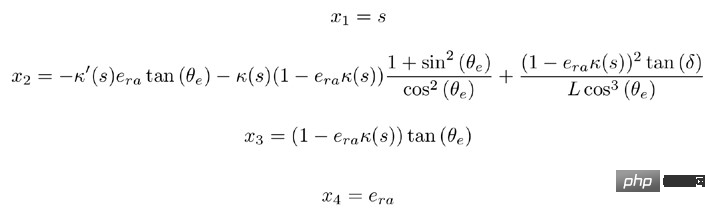
Après le budget intégral inverse, le taux de contrôle peut être obtenu :

1.3.3 Lyapunov
Basé sur Li Yap La conception de la méthode de stabilité Nove peut être appliquée aux modèles cinématiques et dynamiques. L'idée de base est d'abord d'établir un modèle cinématique ou dynamique, de proposer une méthode de suivi basée sur le modèle, puis d'établir une fonction de Lyapunov pour prouver la stabilité asymptotique du système en boucle fermée via la stabilité de Lyapunov [4].
- Modèle cinématique
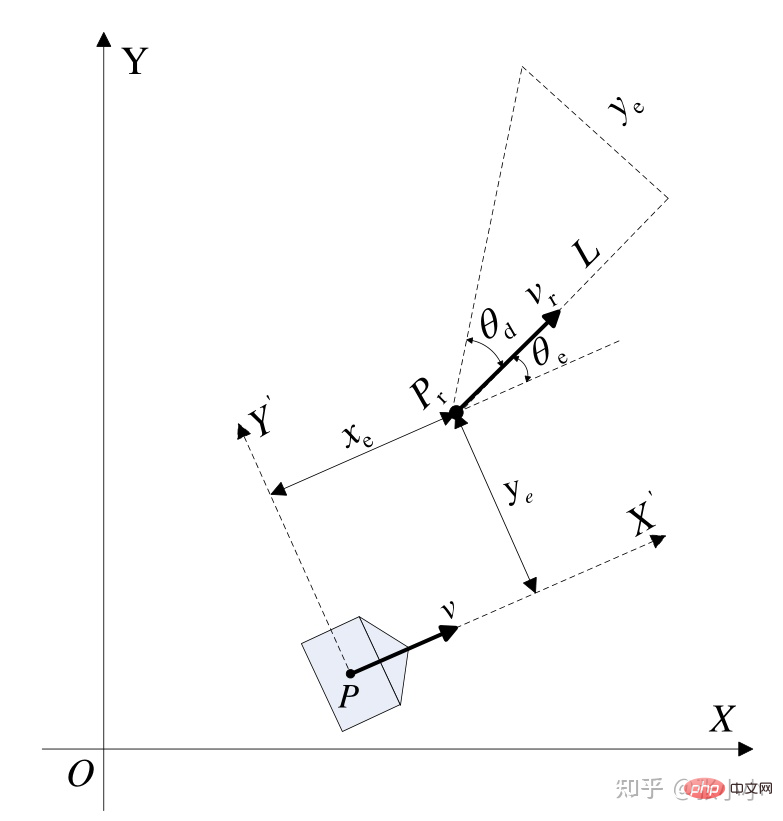
Comme le montre la figure ci-dessus, le point actuel de la voiture est P et le point cible de suivi est Pr. est la différence de pose entre la position actuelle et le point cible, et sont respectivement la vitesse de référence et la vitesse angulaire. Conception de la fonction Lyapunov :

Conception du taux de suivi :
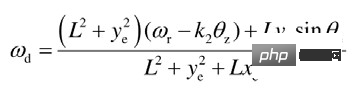
Enfin, en limitant les paramètres de conception des contraintes, la stabilité asymptotique du taux de suivi est prouvée, c'est-à-dire lorsque → ∞, → 0 .
- Modèle dynamique
Établissez d'abord le modèle cinétique :
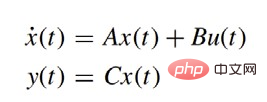
où :

commander

Alors l'erreur est :

Fonction de coût de conception :
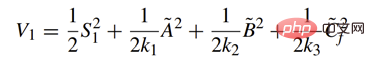
Taux de contrôle de conception :
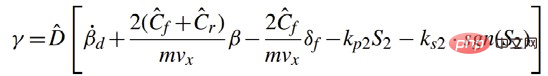
Prouvez enfin la stabilité asymptotique.
1.3.4 Pure Pursuit
Pure tracking est un contrôleur de suivi de chemin géométrique. Ce contrôleur utilise la relation géométrique entre le mouvement du véhicule et la trajectoire de référence pour suivre le contrôleur de la trajectoire de référence. Cette méthode de contrôle utilise le centre de l'essieu arrière du véhicule comme point de référence.

Selon la figure ci-dessus, la commande d'angle de roue avant peut être dérivée :

où R est le rayon de braquage, L est l'empattement du véhicule et e est l'attitude actuelle du véhicule et du waypoint cible dans la direction latérale L'erreur de , est la distance de visée avant et .

Selon les données expérimentales de la figure ci-dessus, à mesure que la distance prospective augmente, la gigue de suivi devient de plus en plus petite. Une distance de guidon plus courte permet un suivi plus précis, tandis qu'une distance de guidon plus longue permet un suivi plus fluide. Une autre caractéristique du PurePursuit est qu'une distance excessive du guidon peut provoquer des « raccourcis » lors du suivi des virages. Le Pure Pursuit est un compromis difficile entre stabilité et performances de suivi.
1.3.5 Stanley
Différent de la méthode de poursuite pure et de suivi pur qui utilise l'axe arrière comme point de référence, le contrôleur Stanley utilise l'axe avant comme point de référence. Il prend en compte à la fois les erreurs de cap et les erreurs latérales. Le contrôleur Stanley prend en compte non seulement les erreurs de cap mais également les erreurs latérales.

Selon la figure ci-dessus, la commande d'angle de la roue avant peut être dérivée :
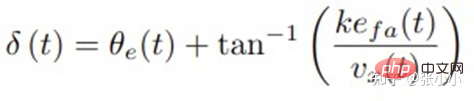
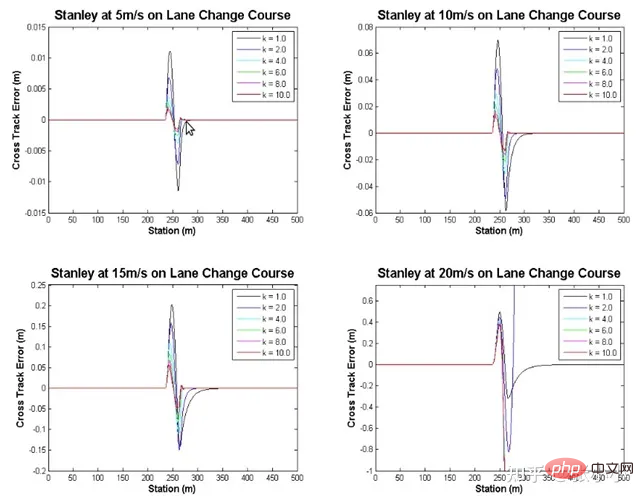
Selon les données expérimentales de la figure ci-dessus, à mesure que k augmente, les performances de suivi seront également s'améliorer. Stanley n'a pas assez de stabilité comme Pure Pursuit lorsque la vitesse du véhicule augmente.
1.3.6 LQR
La méthode basée sur le modèle cinématique du véhicule ignore les caractéristiques dynamiques du véhicule, de sorte que l'algorithme ne peut pas satisfaire le contrôle de stabilité du véhicule lorsque la vitesse du véhicule est trop rapide ou que la courbure change Le taux est trop élevé. Pour les méthodes de contrôle basées sur des modèles de dynamique du véhicule, la tâche principale est de modéliser la dynamique du véhicule. Étant donné que le modèle dynamique précis à deux degrés de liberté est non linéaire, afin de faciliter les calculs de contrôle de suivi en temps réel, il est généralement nécessaire de faire quelques approximations simplifiées basées sur le modèle dynamique précis à deux degrés de liberté pour obtenir un modèle dynamique linéaire à deux degrés de liberté.
- Modèle dynamique à deux degrés de liberté du véhicule :


- LQR :
Le régulateur quadratique linéaire (LQR) est un contrôleur basé sur un modèle, qui utilise l'état du véhicule pour minimiser l'erreur. La théorie LQR est la méthode de conception d’espace d’état la plus ancienne et la plus mature de la théorie du contrôle moderne. LQR peut obtenir la loi de contrôle optimale de la rétroaction linéaire d'état et est facile à former un contrôle optimal en boucle fermée.
La conception optimale de LQR signifie que le contrôleur de rétroaction d'état conçu K doit minimiser la fonction objectif quadratique J, et K est déterminé de manière unique par les matrices de poids Q et R, de sorte que la sélection de Q et R est particulièrement importante. La formule suivante est la fonction de coût LQR :
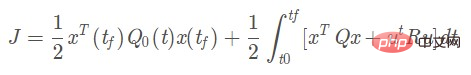
Selon le modèle de dynamique du véhicule et la fonction de coût LQR, l'équation algébrique de Riccati peut être dérivée :

Enfin, la matrice de rétroaction est calculé via l'équation itérative de Riccati, puis obtenir la quantité de contrôle optimale en fonction de la matrice de rétroaction.
1.3.7 MPC
MPC (Model Prediction Control) est un type de problème de contrôle d'optimisation dédié à la décomposition de périodes plus longues, voire infinies, en plusieurs périodes plus courtes, ou périodes de temps finies. problème dans un laps de temps, tout en poursuivant la solution optimale dans une certaine mesure.
MPC se compose des trois éléments suivants :
- Modèle de prédiction : le modèle de prédiction peut très bien prédire les changements dans l'état du système dans un court laps de temps
- Optimisation continue en ligne : étant donné que les résultats obtenus par le modèle de prédiction s'écartent toujours de la situation réelle, l'optimisation continue est utilisé pour trouver chaque instant Pour la solution optimale locale sous le problème, généralement une fonction cible (perte) sera conçue et convertie en un problème de programmation quadratique pour trouver la solution optimale
- Correction du feedback : refaites-le selon ; le nouvel état au prochain instant Prédiction et optimisation.
- Modèle de prédiction :
Un modèle de prédiction peut être dérivé sur la base du modèle de dynamique du véhicule dans LQR.
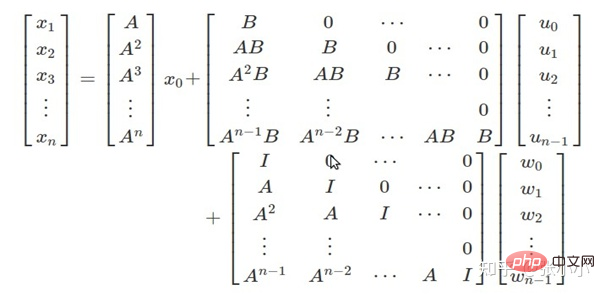

- Optimisation du roulement :
Fonction de coût MPC :
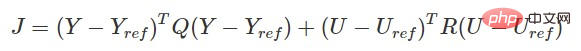
Sur la base du modèle de prédiction, des contraintes latérales du véhicule et de la fonction de coût, le contrôle correspondant les instructions peuvent être obtenu par optimisation et résolution.
1.3.8 Comparaison des algorithmes de contrôle horizontal

1.4 Vertical
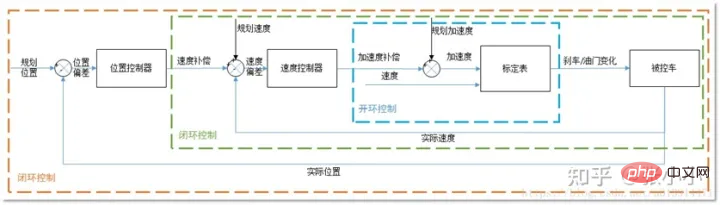
Comme le montre la figure ci-dessus, le contrôle vertical utilise généralement la méthode de contrôle pid en cascade.
2 Conception détaillée
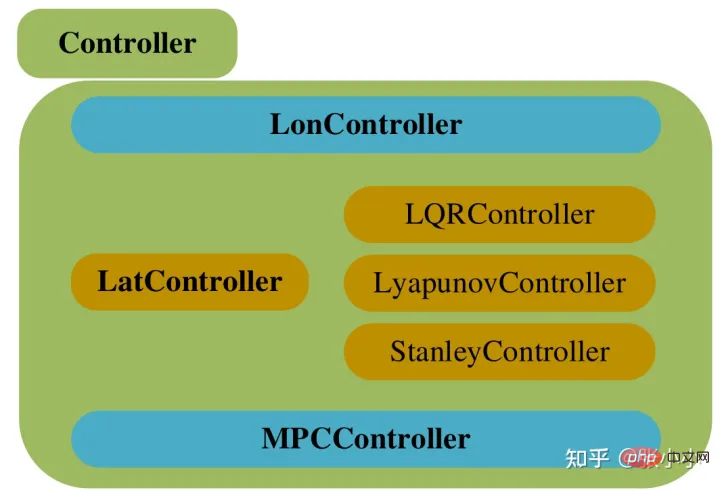
La conception du contrôleur est celle indiquée dans la figure ci-dessus, où Controller est la classe de base et LonController, LonController et MPCController héritent de cette classe de base. LonController a dérivé des sous-classes telles que LQRController, LyapunovController et StanleyController.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Les traits du visage volent, ouvrent la bouche, regardent fixement et lèvent les sourcils. L'IA peut les imiter parfaitement, ce qui rend impossible la prévention des escroqueries vidéo.
Dec 14, 2023 pm 11:30 PM
Les traits du visage volent, ouvrent la bouche, regardent fixement et lèvent les sourcils. L'IA peut les imiter parfaitement, ce qui rend impossible la prévention des escroqueries vidéo.
Dec 14, 2023 pm 11:30 PM
Avec une capacité d'imitation de l'IA aussi puissante, il est vraiment impossible de l'empêcher. Le développement de l’IA a-t-il atteint ce niveau aujourd’hui ? Votre pied avant fait voler les traits de votre visage, et sur votre pied arrière, la même expression est reproduite. Regarder fixement, lever les sourcils, faire la moue, aussi exagérée que soit l'expression, tout est parfaitement imité. Augmentez la difficulté, haussez les sourcils, ouvrez plus grand les yeux, et même la forme de la bouche est tordue, et l'avatar du personnage virtuel peut parfaitement reproduire l'expression. Lorsque vous ajustez les paramètres à gauche, l'avatar virtuel à droite modifiera également ses mouvements en conséquence pour donner un gros plan de la bouche et des yeux. On ne peut pas dire que l'imitation soit exactement la même, seule l'expression est exactement la même. idem (extrême droite). La recherche provient d'institutions telles que l'Université technique de Munich, qui propose GaussianAvatars, qui
 MotionLM : technologie de modélisation de langage pour la prédiction de mouvement multi-agents
Oct 13, 2023 pm 12:09 PM
MotionLM : technologie de modélisation de langage pour la prédiction de mouvement multi-agents
Oct 13, 2023 pm 12:09 PM
Cet article est reproduit avec la permission du compte public Autonomous Driving Heart. Veuillez contacter la source pour la réimpression. Titre original : MotionLM : Multi-Agent Motion Forecasting as Language Modeling Lien vers l'article : https://arxiv.org/pdf/2309.16534.pdf Affiliation de l'auteur : Conférence Waymo : ICCV2023 Idée d'article : Pour la planification de la sécurité des véhicules autonomes, prédisez de manière fiable le comportement futur des agents routiers est cruciale. Cette étude représente les trajectoires continues sous forme de séquences de jetons de mouvement discrets et traite la prédiction de mouvement multi-agents comme une tâche de modélisation du langage. Le modèle que nous proposons, MotionLM, présente les avantages suivants :
 Le robot humanoïde universel intelligent GR-1 Fourier est sur le point de commencer la prévente !
Sep 27, 2023 pm 08:41 PM
Le robot humanoïde universel intelligent GR-1 Fourier est sur le point de commencer la prévente !
Sep 27, 2023 pm 08:41 PM
Le robot humanoïde, qui mesure 1,65 mètre, pèse 55 kilogrammes et possède 44 degrés de liberté dans son corps, peut marcher rapidement, éviter les obstacles rapidement, monter et descendre régulièrement les pentes et résister aux chocs et aux interférences. Vous pouvez désormais le ramener chez vous. ! Le robot humanoïde universel GR-1 de Fourier Intelligence a commencé la prévente. Salle de conférence Robot Le robot humanoïde universel Fourier GR-1 de Fourier Intelligence est maintenant ouvert à la prévente. GR-1 a une configuration de tronc hautement bionique et un contrôle de mouvement anthropomorphique. Il a 44 degrés de liberté dans tout le corps. Il a la capacité de marcher, d'éviter les obstacles, de franchir des obstacles, de monter et de descendre des pentes, de résister aux interférences et de s'adapter. à différentes surfaces routières. C'est un système d'intelligence artificielle général. Page de prévente du site officiel : www.fftai.cn/order#FourierGR-1# Fourier Intelligence doit être réécrit.
 Savez-vous que les programmeurs seront en déclin dans quelques années ?
Nov 08, 2023 am 11:17 AM
Savez-vous que les programmeurs seront en déclin dans quelques années ?
Nov 08, 2023 am 11:17 AM
Le magazine "ComputerWorld" a écrit un article disant que "la programmation disparaîtra d'ici 1960" parce qu'IBM a développé un nouveau langage FORTRAN, qui permet aux ingénieurs d'écrire les formules mathématiques dont ils ont besoin, puis de les soumettre à l'ordinateur pour que la programmation se termine. Picture Quelques années plus tard, nous avons entendu un nouveau dicton : tout homme d'affaires peut utiliser des termes commerciaux pour décrire ses problèmes et dire à l'ordinateur quoi faire. Grâce à ce langage de programmation appelé COBOL, les entreprises n'ont plus besoin de programmeurs. Plus tard, il est dit qu'IBM a développé un nouveau langage de programmation appelé RPG qui permet aux employés de remplir des formulaires et de générer des rapports, de sorte que la plupart des besoins de programmation de l'entreprise puissent être satisfaits grâce à lui.
 Quelles sont les méthodes efficaces et les méthodes de base communes pour la prédiction de trajectoires piétonnes ? Partage des meilleurs articles de conférence !
Oct 17, 2023 am 11:13 AM
Quelles sont les méthodes efficaces et les méthodes de base communes pour la prédiction de trajectoires piétonnes ? Partage des meilleurs articles de conférence !
Oct 17, 2023 am 11:13 AM
La prédiction de trajectoire a pris de l'ampleur au cours des deux dernières années, mais l'essentiel se concentre sur la direction de la prédiction de trajectoire des véhicules. Aujourd'hui, Autonomous Driving Heart partagera avec vous l'algorithme de prédiction de trajectoire des piétons sur NeurIPS - SHENet. les schémas de déplacement sont généralement, dans une certaine mesure, conformes à des règles limitées. Sur la base de cette hypothèse, SHENet prédit la trajectoire future d'une personne en apprenant des règles de scène implicites. L'article a été autorisé comme original par Autonomous Driving Heart ! La compréhension personnelle de l'auteur est qu'à l'heure actuelle, prédire la trajectoire future d'une personne reste un problème difficile en raison du caractère aléatoire et subjectif du mouvement humain. Cependant, les schémas de mouvement humain dans les scènes contraintes varient souvent en raison des contraintes de la scène (telles que les plans d'étage, les routes et les obstacles) et de l'interactivité d'humain à humain ou d'humain à objet.
 Huawei lancera le système de détection Xuanji dans le domaine des appareils portables intelligents, capable d'évaluer l'état émotionnel de l'utilisateur en fonction de la fréquence cardiaque
Aug 29, 2024 pm 03:30 PM
Huawei lancera le système de détection Xuanji dans le domaine des appareils portables intelligents, capable d'évaluer l'état émotionnel de l'utilisateur en fonction de la fréquence cardiaque
Aug 29, 2024 pm 03:30 PM
Récemment, Huawei a annoncé qu'il lancerait en septembre un nouveau produit portable intelligent équipé du système de détection Xuanji, qui devrait être la dernière montre intelligente de Huawei. Ce nouveau produit intégrera des fonctions avancées de surveillance de la santé émotionnelle. Le système de perception Xuanji fournit aux utilisateurs une évaluation complète de la santé avec ses six caractéristiques : précision, exhaustivité, rapidité, flexibilité, ouverture et évolutivité. Le système utilise un module de super-détection et optimise la technologie d'architecture de chemin optique multicanal, ce qui améliore considérablement la précision de surveillance des indicateurs de base tels que la fréquence cardiaque, l'oxygène dans le sang et la fréquence respiratoire. En outre, le système de détection Xuanji a également élargi la recherche sur les états émotionnels sur la base des données de fréquence cardiaque. Il ne se limite pas aux indicateurs physiologiques, mais peut également évaluer l'état émotionnel et le niveau de stress de l'utilisateur. Il prend en charge la surveillance de plus de 60 sports. indicateurs de santé, couvrant les domaines cardiovasculaire, respiratoire, neurologique, endocrinien,
 Ma montre intelligente ne s'allume pas : que faire maintenant
Aug 23, 2023 pm 05:41 PM
Ma montre intelligente ne s'allume pas : que faire maintenant
Aug 23, 2023 pm 05:41 PM
Que faire si votre montre connectée ne s'allume pas ? Voici les options disponibles pour restaurer la vie de votre montre intelligente bien-aimée. VÉRIFIEZ POWER PLAY : Imaginez une scène remplie de stars avec votre montre intelligente en tête d'affiche, mais les rideaux ne se lèvent pas parce qu'elle a oublié la batterie ! Avant d'entrer dans les détails, assurez-vous que votre montre intelligente ne fonctionne pas uniquement sur de la fumée et des miroirs. Donnez-lui un temps de charge approprié et si vous vous sentez un peu plus, offrez-lui un nouveau câble élégant – du genre avant-gardiste ! Reboot fantastique : en cas de doute, donnez-lui un peu de R&R : c'est Reboot and Revival ! Appuyez et maintenez ces boutons comme un maestro dirigeant une symphonie. Différentes montres intelligentes ont leurs propres rituels de redémarrage – Google est votre guide. C'est un
 UniOcc : Unifier la prédiction d'occupation centrée sur la vision avec un rendu géométrique et sémantique !
Sep 16, 2023 pm 08:29 PM
UniOcc : Unifier la prédiction d'occupation centrée sur la vision avec un rendu géométrique et sémantique !
Sep 16, 2023 pm 08:29 PM
Titre original : UniOcc : UnifyingVision-Centric3DOccupancyPredictionwithGeometricandSemanticRendering Veuillez cliquer sur le lien suivant pour consulter l'article : https://arxiv.org/pdf/2306.09117.pdf Idée d'article : Dans ce rapport technique, nous proposons une solution appelée UniOCC, utilisant For vision- trajectoires de prédiction d'occupation 3D centrées dans CVPR2023nuScenesOpenDatasetChallenge. Les méthodes de prévision d'occupation existantes se concentrent principalement sur l'utilisation d'étiquettes d'occupation tridimensionnelles.





