Périphériques technologiques
IA
10 lignes de code pour compléter le graphique Transformer, le cadre de réseau neuronal graphique DGL a inauguré la version 1.0
10 lignes de code pour compléter le graphique Transformer, le cadre de réseau neuronal graphique DGL a inauguré la version 1.0
En 2019, l'Université de New York et Amazon Cloud Technology ont lancé conjointement le framework de réseau neuronal graphique DGL (Deep Graph Library). Maintenant, DGL 1.0 est officiellement publié ! DGL 1.0 résume les différents besoins en matière d'apprentissage profond des graphes et de technologie de réseau neuronal graphique (GNN) dans le monde universitaire ou industriel au cours des trois dernières années. De la recherche universitaire sur des modèles de pointe à la mise à l'échelle des GNN vers des applications industrielles, DGL 1.0 fournit une solution complète et facile à utiliser pour que tous les utilisateurs puissent mieux tirer parti de l'apprentissage automatique des graphes.
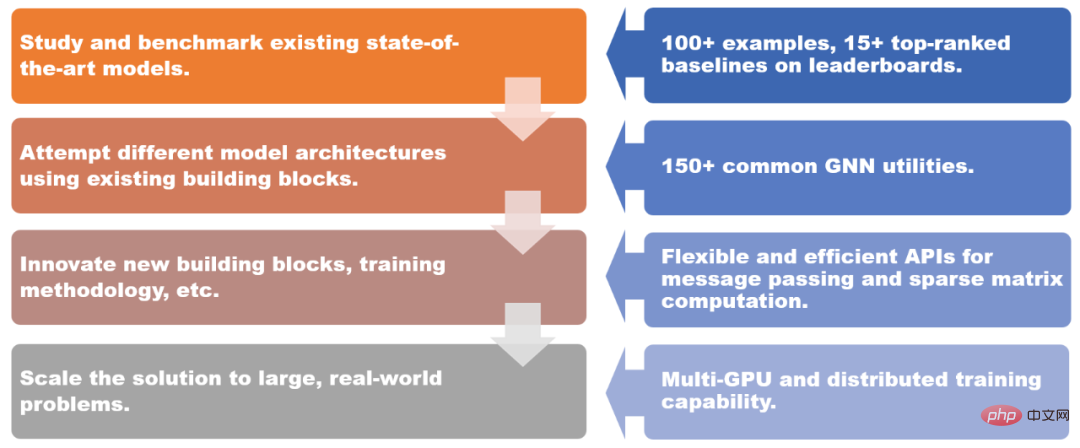
DGL 1.0 fournit des solutions pour différents scénarios.
DGL 1.0 adopte une conception en couches et modulaire pour répondre aux différents besoins des utilisateurs. Les principales fonctionnalités de cette version incluent :
- +100 exemples de modèles GNN prêts à l'emploi, plus de 15 modèles de référence les mieux classés sur Open Graph Benchmark (OGB) ;
- +150 modules GNN communs, y compris les couches GNN, les ensembles de données, les modules de conversion de données graphiques, les échantillonneurs graphiques, etc., peuvent être utilisés pour créer de nouvelles architectures de modèles ou des solutions basées sur GNN
- Transmission de messages flexible et efficace et abstraction matricielle clairsemée, en utilisant Pour le développement ; de nouveaux modules GNN ;
- Les capacités de formation multi-GPU et distribuées prennent en charge la formation sur des dizaines de milliards de graphiques.
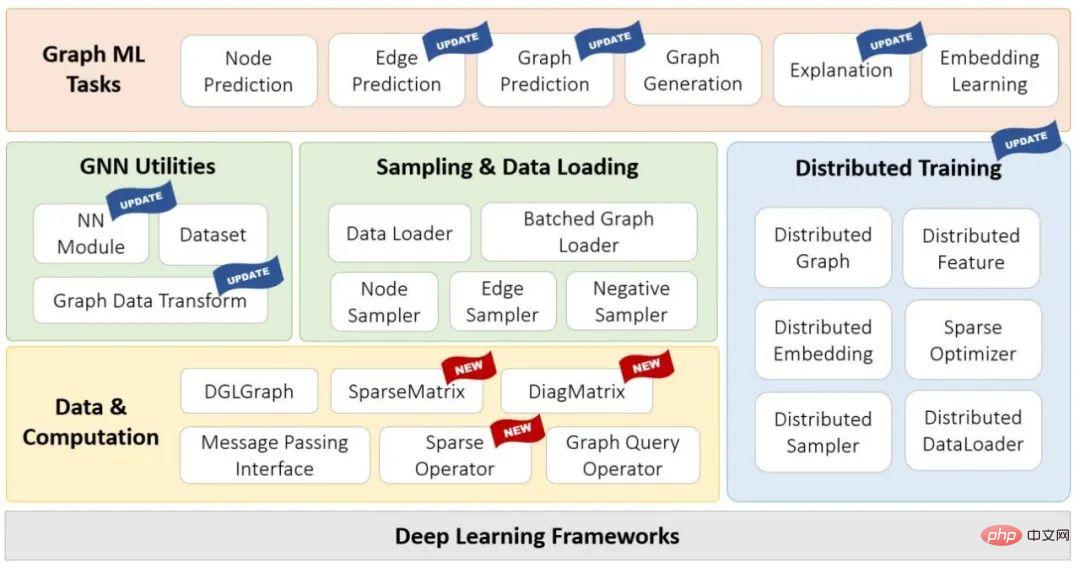
Diagramme de la pile technologique DGL 1.0
Adresse : https://github.com/dmlc/dgl
L'un des points forts de cette version est l'introduction de DGL-Sparse, une nouvelle interface de programmation qui utilise des matrices clairsemées comme abstraction de programmation principale. DGL-Sparse simplifie non seulement le développement de modèles GNN existants (tels que les réseaux convolutionnels graphes), mais fonctionne également avec les modèles les plus récents, notamment les GNN basés sur la diffusion, les réseaux neuronaux hypergraphiques et les transformateurs graphiques.
La sortie de la version 1.0 de DGL a suscité des réactions enthousiastes sur Internet. Des chercheurs tels que Yann Lecun, l'un des trois géants du deep learning, et Xavier Bresson, professeur agrégé à l'Université nationale de Singapour, ont tous apprécié et l'a transmis.
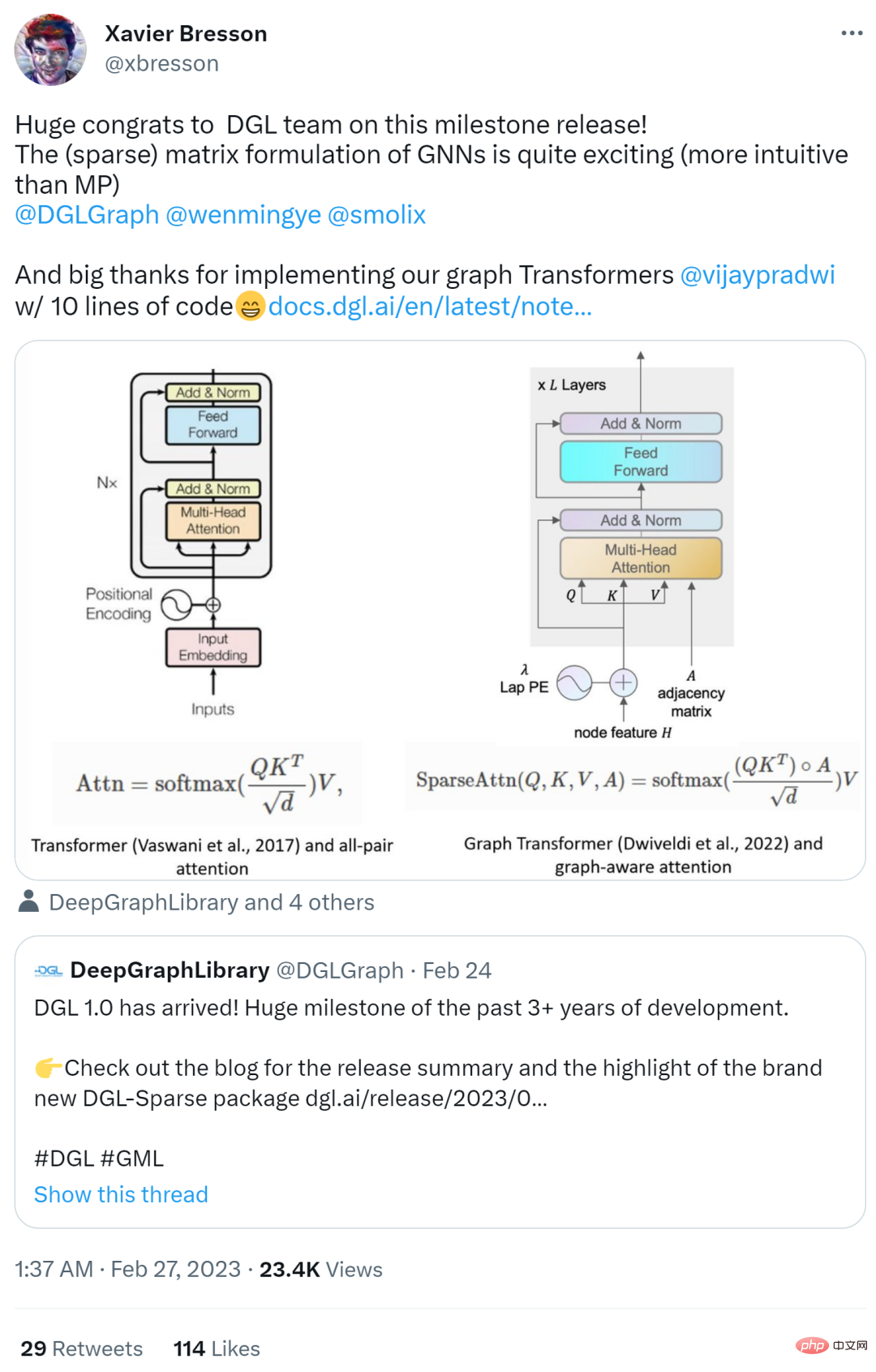
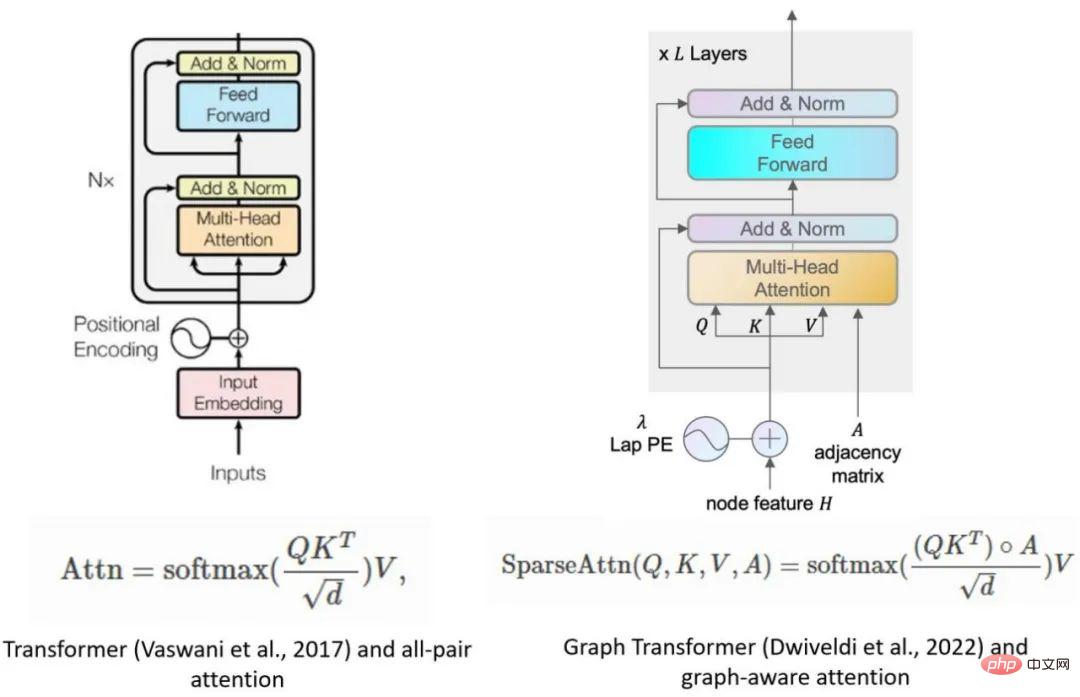
Dans l'article suivant, l'auteur décrit deux paradigmes GNN traditionnels, à savoir la vue de transmission de messages et la vue matricielle. Ces paradigmes peuvent aider les chercheurs à mieux comprendre le mécanisme de fonctionnement interne du GNN, et la perspective matricielle est également l'une des motivations du développement de DGL Sparse.
Vue de passage de messages et vue matricielle
Il y a un dicton dans le film "Arrivée": "La langue que vous utilisez détermine votre façon de penser et affecte votre vision des choses." Cette phrase convient également à GNN.
signifie que les réseaux de neurones graphes ont deux paradigmes différents. La première, appelée vue de transmission de messages, exprime le modèle GNN d'un point de vue local et précis, détaillant comment les messages sont échangés le long des bords et comment les états des nœuds sont mis à jour en conséquence. La seconde est la perspective matricielle. Étant donné que les graphiques ont une équivalence algébrique avec des matrices d’adjacence clairsemées, de nombreux chercheurs choisissent d’exprimer les modèles GNN dans une perspective globale à gros grain, en mettant l’accent sur les opérations impliquant des matrices d’adjacence clairsemées et des vecteurs propres.
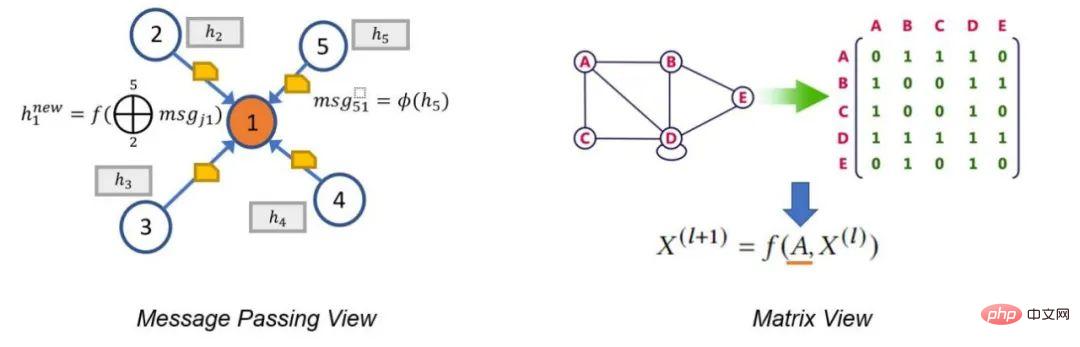
La perspective de transmission de messages révèle le lien entre les GNN et le test d'isomorphisme des graphes de Weisfeiler Lehman (WL), qui repose également sur l'agrégation d'informations provenant des voisins. La perspective matricielle comprend GNN d'un point de vue algébrique, conduisant à des découvertes intéressantes, telles que le problème du sur-lissage.
En bref, ces deux perspectives sont des outils indispensables pour étudier le GNN. Elles se complètent et aident les chercheurs à mieux comprendre et décrire la nature et les caractéristiques des modèles GNN. C'est pour cette raison que l'une des principales motivations de la sortie de DGL 1.0 est d'ajouter le support de la perspective matricielle basée sur l'interface de transmission de messages existante.
DGL Sparse : une bibliothèque de matrices clairsemées conçue pour l'apprentissage automatique des graphes
La version DGL 1.0 possède une nouvelle bibliothèque appelée DGL Sparse (dgl.sparse), qui, avec l'interface de transmission de messages dans DGL, améliore la prise en charge de tous les types de modèles de réseaux neuronaux graphiques. DGL Sparse fournit des classes et des opérations matricielles clairsemées spécifiquement pour l'apprentissage automatique des graphes, ce qui facilite l'écriture de GNN d'un point de vue matriciel. Dans la section suivante, les auteurs présentent plusieurs exemples de GNN, montrant leurs formulations mathématiques et les implémentations de code correspondantes dans DGL Sparse.
Graph Convolutional Network
GCN est l'un des pionniers de la modélisation GNN. GCN peut être représenté à la fois avec une vue de transmission de messages et une vue matricielle. Le code suivant compare les différences entre ces deux méthodes dans DGL.
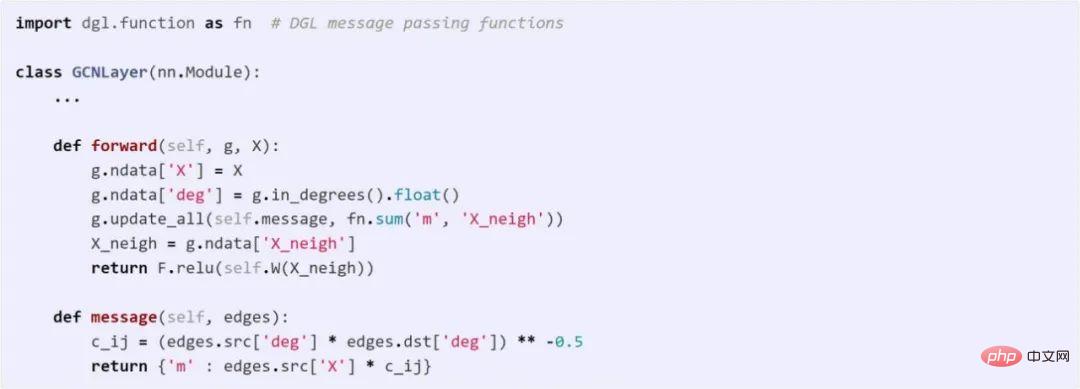
Utilisez l'API de messagerie pour implémenter GCN
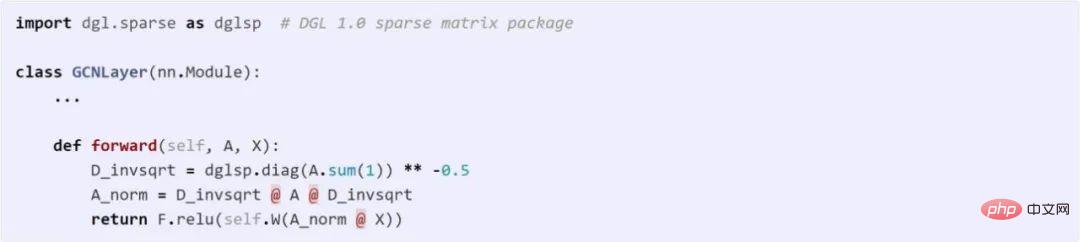
Utilisation de DGL Sparse pour implémenter GCN
GNN basé sur la diffusion graphique
La diffusion graphique est le processus de propagation ou de lissage des caractéristiques ou des signaux des nœuds le long des bords. De nombreux algorithmes graphiques classiques tels que le PageRank entrent dans cette catégorie. Une série d'études ont montré que la combinaison de la diffusion de graphes avec des réseaux de neurones est un moyen efficace et efficient d'améliorer les prédictions des modèles. L'équation suivante décrit le calcul de base de l'un des modèles les plus représentatifs, APPNP. Il peut être implémenté directement dans DGL Sparse.
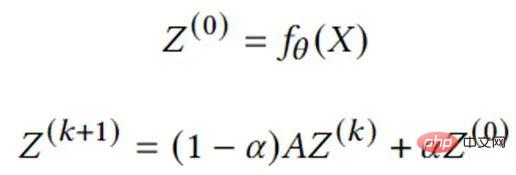
Réseau neuronal hypergraphique
Un hypergraphe est une généralisation de graphiques où les arêtes peuvent connecter n'importe quel nombre de nœuds (appelés hyperedges). Les hypergraphes sont particulièrement utiles dans les scénarios où des relations d'ordre supérieur doivent être capturées, comme le comportement de co-achat sur les plateformes de commerce électronique ou la co-auteur dans les réseaux de citations. Une caractéristique typique d'un hypergraphe est sa matrice de corrélation clairsemée, de sorte que les réseaux de neurones hypergraphiques (HGNN) sont souvent définis à l'aide de matrices clairsemées. Ce qui suit est un réseau convolutionnel hypergraphique (Feng et al., 2018) et son implémentation de code. Le modèle Transformer est devenu l'architecture de modèle la plus performante en matière de traitement du langage naturel. Les chercheurs commencent également à étendre Transformer à l’apprentissage automatique graphique. Dwivedi et al. ont été les pionniers de l'idée de limiter toute attention multi-têtes aux paires de nœuds connectées dans le graphique. Ce modèle peut être facilement implémenté avec seulement 10 lignes de code à l'aide de l'outil DGL Sparse.
Principales fonctionnalités de DGL Sparse
Par rapport aux bibliothèques matricielles clairsemées telles que scipy.sparse ou torch.sparse, la conception globale de DGL Sparse est de servir l'apprentissage automatique des graphes, y compris Les fonctionnalités clés suivantes :
- Sélection automatique du format clairsemé : DGL Sparse est conçu pour que les utilisateurs n'aient pas à se soucier du choix de la bonne structure de données pour stocker les matrices clairsemées (également appelées formats clairsemés). ). Les utilisateurs doivent seulement se rappeler que dgl.sparse.spmatrix crée une matrice clairsemée et que DGL sélectionnera automatiquement en interne le format optimal en fonction de l'opérateur appelé
- éléments scalaires ou vectoriels non nuls : a ; Les modèles GNN apprennent plusieurs poids sur les bords (tels que les vecteurs d'attention multi-têtes démontrés dans l'exemple Graph Transformer). Pour s'adapter à cette situation, DGL Sparse permet aux éléments non nuls d'avoir des formes vectorielles et étend les opérations clairsemées courantes telles que la multiplication de matrice clairsemée-dense (SpMM), etc. Vous pouvez vous référer à l'opération bspmm dans l'exemple de Graph Transformer.
En tirant parti de ces fonctionnalités de conception, DGL Sparse réduit la longueur du code de 2,7x en moyenne par rapport aux implémentations précédentes de modèles de vue matricielle utilisant des interfaces de transmission de messages. Le code simplifié réduit également la surcharge du framework de 43%. De plus, DGL Sparse est compatible avec PyTorch et peut être facilement intégré à divers outils et packages de l'écosystème PyTorch.
Démarrez avec DGL 1.0
DGL 1.0 a été publié sur toutes les plates-formes et peut être facilement installé à l'aide de pip ou conda. En plus des exemples présentés précédemment, la première version de DGL Sparse comprend également 5 didacticiels et 11 exemples de bout en bout, qui peuvent tous être expérimentés directement dans Google Colab sans nécessiter d'installation locale.
Pour en savoir plus sur les nouvelles fonctionnalités de DGL 1.0, veuillez vous référer au journal de publication de l'auteur. Si vous rencontrez des problèmes ou avez des suggestions ou des commentaires lors de l'utilisation de DGL, vous pouvez également contacter l'équipe DGL via le forum de discussion ou Slack.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Outils d'IA chauds
Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes
AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.
Undress AI Tool
Images de déshabillage gratuites
Clothoff.io
Dissolvant de vêtements AI
AI Hentai Generator
Générez AI Hentai gratuitement.
Article chaud
Outils chauds
Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit
SublimeText3 version chinoise
Version chinoise, très simple à utiliser
Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP
Dreamweaver CS6
Outils de développement Web visuel
SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
Cet article vous amènera à comprendre SHAP : explication du modèle pour l'apprentissage automatique
Jun 01, 2024 am 10:58 AM
Dans les domaines de l’apprentissage automatique et de la science des données, l’interprétabilité des modèles a toujours été au centre des préoccupations des chercheurs et des praticiens. Avec l'application généralisée de modèles complexes tels que l'apprentissage profond et les méthodes d'ensemble, la compréhension du processus décisionnel du modèle est devenue particulièrement importante. Explainable AI|XAI contribue à renforcer la confiance dans les modèles d'apprentissage automatique en augmentant la transparence du modèle. L'amélioration de la transparence des modèles peut être obtenue grâce à des méthodes telles que l'utilisation généralisée de plusieurs modèles complexes, ainsi que les processus décisionnels utilisés pour expliquer les modèles. Ces méthodes incluent l'analyse de l'importance des caractéristiques, l'estimation de l'intervalle de prédiction du modèle, les algorithmes d'interprétabilité locale, etc. L'analyse de l'importance des fonctionnalités peut expliquer le processus de prise de décision du modèle en évaluant le degré d'influence du modèle sur les fonctionnalités d'entrée. Estimation de l’intervalle de prédiction du modèle
Transparent! Une analyse approfondie des principes des principaux modèles de machine learning !
Apr 12, 2024 pm 05:55 PM
En termes simples, un modèle d’apprentissage automatique est une fonction mathématique qui mappe les données d’entrée à une sortie prédite. Plus précisément, un modèle d'apprentissage automatique est une fonction mathématique qui ajuste les paramètres du modèle en apprenant à partir des données d'entraînement afin de minimiser l'erreur entre la sortie prédite et la véritable étiquette. Il existe de nombreux modèles dans l'apprentissage automatique, tels que les modèles de régression logistique, les modèles d'arbre de décision, les modèles de machines à vecteurs de support, etc. Chaque modèle a ses types de données et ses types de problèmes applicables. Dans le même temps, il existe de nombreux points communs entre les différents modèles, ou il existe une voie cachée pour l’évolution du modèle. En prenant comme exemple le perceptron connexionniste, en augmentant le nombre de couches cachées du perceptron, nous pouvons le transformer en un réseau neuronal profond. Si une fonction noyau est ajoutée au perceptron, elle peut être convertie en SVM. celui-ci
Identifier le surapprentissage et le sous-apprentissage grâce à des courbes d'apprentissage
Apr 29, 2024 pm 06:50 PM
Cet article présentera comment identifier efficacement le surajustement et le sous-apprentissage dans les modèles d'apprentissage automatique grâce à des courbes d'apprentissage. Sous-ajustement et surajustement 1. Surajustement Si un modèle est surentraîné sur les données de sorte qu'il en tire du bruit, alors on dit que le modèle est en surajustement. Un modèle surajusté apprend chaque exemple si parfaitement qu'il classera mal un exemple inédit/inédit. Pour un modèle surajusté, nous obtiendrons un score d'ensemble d'entraînement parfait/presque parfait et un score d'ensemble/test de validation épouvantable. Légèrement modifié : "Cause du surajustement : utilisez un modèle complexe pour résoudre un problème simple et extraire le bruit des données. Parce qu'un petit ensemble de données en tant qu'ensemble d'entraînement peut ne pas représenter la représentation correcte de toutes les données."
L'évolution de l'intelligence artificielle dans l'exploration spatiale et l'ingénierie des établissements humains
Apr 29, 2024 pm 03:25 PM
Dans les années 1950, l’intelligence artificielle (IA) est née. C’est à ce moment-là que les chercheurs ont découvert que les machines pouvaient effectuer des tâches similaires à celles des humains, comme penser. Plus tard, dans les années 1960, le Département américain de la Défense a financé l’intelligence artificielle et créé des laboratoires pour poursuivre son développement. Les chercheurs trouvent des applications à l’intelligence artificielle dans de nombreux domaines, comme l’exploration spatiale et la survie dans des environnements extrêmes. L'exploration spatiale est l'étude de l'univers, qui couvre l'ensemble de l'univers au-delà de la terre. L’espace est classé comme environnement extrême car ses conditions sont différentes de celles de la Terre. Pour survivre dans l’espace, de nombreux facteurs doivent être pris en compte et des précautions doivent être prises. Les scientifiques et les chercheurs pensent qu'explorer l'espace et comprendre l'état actuel de tout peut aider à comprendre le fonctionnement de l'univers et à se préparer à d'éventuelles crises environnementales.
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
IA explicable : Expliquer les modèles IA/ML complexes
Jun 03, 2024 pm 10:08 PM
Traducteur | Revu par Li Rui | Chonglou Les modèles d'intelligence artificielle (IA) et d'apprentissage automatique (ML) deviennent aujourd'hui de plus en plus complexes, et le résultat produit par ces modèles est une boîte noire – impossible à expliquer aux parties prenantes. L'IA explicable (XAI) vise à résoudre ce problème en permettant aux parties prenantes de comprendre comment fonctionnent ces modèles, en s'assurant qu'elles comprennent comment ces modèles prennent réellement des décisions et en garantissant la transparence des systèmes d'IA, la confiance et la responsabilité pour résoudre ce problème. Cet article explore diverses techniques d'intelligence artificielle explicable (XAI) pour illustrer leurs principes sous-jacents. Plusieurs raisons pour lesquelles l’IA explicable est cruciale Confiance et transparence : pour que les systèmes d’IA soient largement acceptés et fiables, les utilisateurs doivent comprendre comment les décisions sont prises
Flash Attention est-il stable ? Meta et Harvard ont constaté que les écarts de poids de leur modèle fluctuaient de plusieurs ordres de grandeur.
May 30, 2024 pm 01:24 PM
MetaFAIR s'est associé à Harvard pour fournir un nouveau cadre de recherche permettant d'optimiser le biais de données généré lors de l'apprentissage automatique à grande échelle. On sait que la formation de grands modèles de langage prend souvent des mois et utilise des centaines, voire des milliers de GPU. En prenant comme exemple le modèle LLaMA270B, sa formation nécessite un total de 1 720 320 heures GPU. La formation de grands modèles présente des défis systémiques uniques en raison de l’ampleur et de la complexité de ces charges de travail. Récemment, de nombreuses institutions ont signalé une instabilité dans le processus de formation lors de la formation des modèles d'IA générative SOTA. Elles apparaissent généralement sous la forme de pics de pertes. Par exemple, le modèle PaLM de Google a connu jusqu'à 20 pics de pertes au cours du processus de formation. Le biais numérique est à l'origine de cette imprécision de la formation,
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
