Le réseau neuronal graphique a été publié dans une sous-revue Nature, mais il a été révélé qu'il était 104 fois plus lent que l'algorithme ordinaire. Questionneurs : est-ce une nouvelle hauteur ?

GNN est un domaine très populaire ces dernières années. Récemment, un article de la sous-revue Nature a proposé une méthode pour utiliser GNN pour résoudre des problèmes d'optimisation combinatoire et a affirmé que les performances de l'optimiseur GNN sont équivalentes, voire supérieures, aux solveurs existants. Cependant, cet article a suscité quelques doutes : certaines personnes ont souligné que les performances de ce GNN ne sont en réalité pas aussi bonnes que celles de l'algorithme glouton classique, et que la vitesse est beaucoup plus lente que l'algorithme glouton (pour les problèmes avec un million de variables, l'algorithme glouton l'algorithme est meilleur que le GNN 104 fois plus rapide). Alors les sceptiques ont dit : « Nous ne voyons aucune bonne raison d’utiliser ces GNN pour résoudre ce problème, c’est comme utiliser un marteau pour casser des noix. Ils espèrent que les auteurs de ces articles pourront d’abord résoudre ce problème difficile avant de revendiquer la solution. » supériorité de la méthode. Comparez les benchmarks.

Ces dernières années, les réseaux de neurones ont résolu de nombreux problèmes difficiles en sciences appliquées et fondamentales, y compris des problèmes d'optimisation combinatoire discrète, qui constituent également la base de notre compréhension des limites de l'informatique.

L'étude 2022 de Martin JA Schuetz et al. "Optimisation combinatoire avec des réseaux de neurones graphistes inspirés de la physique" [4] propose d'utiliser des réseaux de neurones graphes non supervisés (GNN) inspirés de la physique pour résoudre des problèmes d'optimisation combinatoire sur les graphes. Cette approche semble prometteuse et a été publiée dans une revue à fort impact (Nature Machine Intelligence). L'étude a testé les performances des GNN sur deux problèmes d'optimisation standard : la coupe maximale et l'ensemble indépendant maximal (MIS). Cet optimiseur GNN récemment proposé possède une propriété très intéressante : il peut être étendu à de nombreux problèmes d'instance plus importants.

Adresse papier : https://arxiv.org/pdf/2107.01188.pdf

Cependant, un nouvel article récent « Casser des noix avec un marteau : quand les réseaux de neurones graphes modernes font pire que "Les algorithmes gourmands classiques" ont remis en question les recherches de Martin JA Schuetz et al., estimant que l'optimiseur GNN proposé par Martin JA Schuetz et al. "casse des noix avec un marteau, semblable à l'utilisation d'un mortier pour frapper les moustiques", ce qui est un. gaspillage de ressources et donne de mauvais résultats.

Adresse papier : https://arxiv.org/abs/2206.13211

MIS Le problème est défini comme suit : Étant donné un régulier aléatoire non orienté avec n nœuds et degré fixé à d Graph ( d-RRG), l'ensemble indépendant (IS) fait référence au sous-ensemble de sommets qui ne contient aucune paire de voisins les plus proches ; le problème MIS nécessite de trouver le plus grand IS, dont la taille est appelée α ; MIS est un problème NP-difficile, mais on souhaite trouver un algorithme pour trouver un SI avec une taille aussi proche que possible du maximum en temps polynomial. De plus, un bon algorithme ne devrait pas subir de dégradation des performances pour des valeurs de n plus élevées.

Le nouveau GNN proposé par Martin JA Schuetz et al. peut trouver IS pour de très grands graphes (n≤ 10^6) : le temps d'exécution de l'algorithme est proportionnel à la taille du problème : t∼ n^1,7, et à l'algorithme. les performances augmentent avec n L'augmentation reste stable, comme le montre la figure 1 ci-dessous.

​

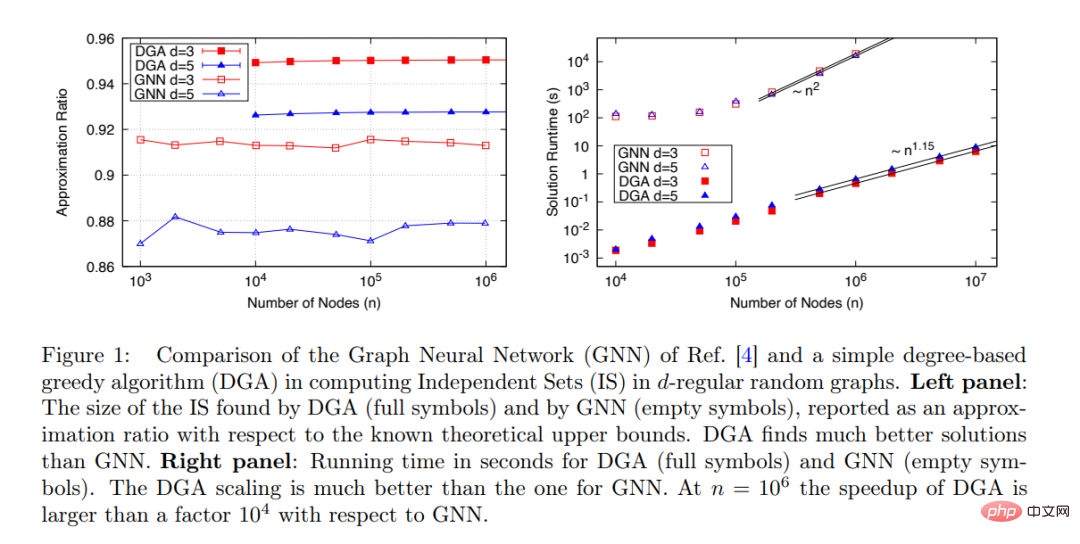
Cependant, en comparant les performances du GNN proposé avec d'autres algorithmes disponibles, l'étude l'a uniquement comparé à l'algorithme d'approximation de Boppana-Halldorsson (BH) [8], qui est utilisé lorsque n≤ À 500, le temps d'exécution est t∼n^2,9. ​

Il existe en fait de nombreux autres algorithmes de calcul de IS qui sont beaucoup plus rapides que BH, et l'étude devrait comparer l'optimiseur GNN proposé avec ces algorithmes. Parmi eux, l’algorithme le plus simple est l’algorithme glouton (GA) [9]. Une fois l’algorithme glouton basé sur le degré (DGA) optimisé, le temps d’exécution est presque linéaire avec le nombre de nœuds n. ​

Cette étude compare les performances de l'optimiseur GNN (ouvert) et DGA (solide) proposés par Martin JA Schuetz et al dans la recherche de MIS sur les d-RRG avec d=3 et d=5. Comme le montre la figure 1 (à droite), du point de vue de la relation entre le temps d'exécution et la taille du problème (nombre de nœuds), DGA est bien meilleur que GNN. Le temps d'exécution du premier est presque linéairement lié au nombre. de nœuds n (l'exposant est 1,15, probablement en raison de l'effet pré-asymptotique), et le temps d'exécution de GNN a une relation presque quadratique avec le nombre de nœuds n.

Cette étude estime que l'affirmation de Martin JA Schuetz et al. selon laquelle « les performances des optimiseurs basés sur des réseaux de neurones graphiques sont équivalentes ou meilleures que celles des solveurs existants, ont la capacité de surpasser le modèle SOTA actuel et peuvent être étendues à "Le problème des millions de variables" ne résiste pas à un examen minutieux et est incompatible avec les résultats expérimentaux réels. Martin JA Schuetz et d'autres devraient réviser l'article. ​

Cette étude clarifie les performances de la DGA en détail et estime que cet algorithme glouton simple doit être considéré comme une référence minimale, et que les performances de tout nouvel algorithme doivent être au moins meilleures que celles de la DGA avant de pouvoir être adoptées.

Bien sûr, DGA n'est qu'un algorithme extrêmement simple, et il existe de nombreux autres algorithmes standards qui sont meilleurs que DGA. L'article de Maria Chiara et al. de 2019 « Les algorithmes de Monte-Carlo sont très efficaces pour trouver le plus grand ensemble indépendant dans des graphiques aléatoires clairsemés » fournit une étude approfondie des performances de plusieurs algorithmes pour résoudre les problèmes MIS. ​

Sur cette base, l'étude soulève une question : "Lors de l'évaluation d'un nouvel algorithme d'optimisation, quels problèmes vraiment difficiles doivent être utilisés comme référence pour tester les performances de l'algorithme

Par exemple, le l'étude estime que dans d 16 MIS sur d-RRG. Ici, les résultats pour d = 20 et d = 100 peuvent être comparés aux résultats donnés dans l'article de 2019 « Les algorithmes de Monte Carlo sont très efficaces pour trouver le plus grand ensemble indépendant dans des graphiques aléatoires clairsemés ».

Évidemment, un bon algorithme d'optimisation doit être complété en un temps polynomial de n. Il serait préférable que la relation soit linéaire. La qualité de la solution trouvée devrait être meilleure que celle des algorithmes simples existants, et elle ne devrait pas augmenter. avec n. augmenté tandis que la qualité diminuait.

L'étude conclut : actuellement, les optimiseurs basés sur les réseaux neuronaux (tels que ceux proposés par Martin JA Schuetz et al.) ne répondent pas aux exigences ci-dessus et ne peuvent pas rivaliser avec des algorithmes standards simples pour résoudre des problèmes d'optimisation difficiles. Il est crucial de déterminer si les réseaux de neurones peuvent répondre à cette exigence ou s’il existe des raisons plus profondes à leur échec.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!