Utilisez Python pour implémenter le suivi automatique des missiles, super gravure !

Bonjour à tous, je suis Frère J.

C'est difficile à calculer sans quelques fondements mathématiques. Mais c'est différent lorsque nous avons des ordinateurs. En nous appuyant sur la vitesse de calcul extrêmement rapide des ordinateurs, nous pouvons y parvenir en utilisant l'idée de différenciation et en ajoutant un peu de connaissances simples en trigonométrie.

D'accord, sans plus tarder, jetons un coup d'œil à son principe d'algorithme. Regardez l'image :

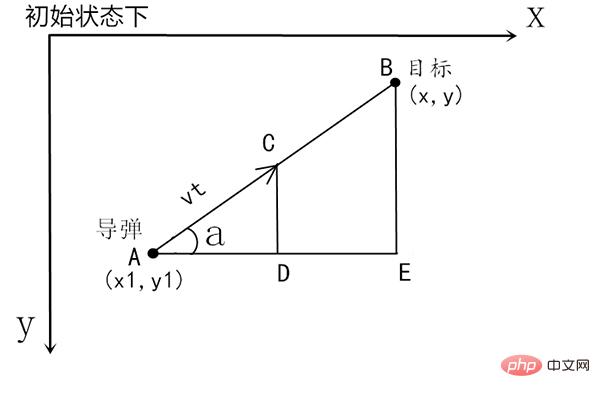
Puisque nous utiliserons pygame pour démontrer plus tard, son système de coordonnées est l'axe y vers le bas, nous utilisons donc également y. ici. Système de coordonnées vers le bas.

L'idée générale de l'algorithme est de diviser le temps t en segments suffisamment petits (par exemple 1/1000, plus la tranche de temps est petite, plus elle est précise) en fonction de la figure ci-dessus. Chaque segment construit le triangle. comme ci-dessus pour calculer la prochaine tranche de temps du missile. La direction de marche (c'est-à-dire ∠a) et la distance parcourue (c'est-à-dire vt=|AC|), à ce moment la cible se déplace à nouveau dans la deuxième tranche de temps, puis la le point C qui vient d'être calculé devient la deuxième fois le point initial de la tranche, puis construisez un triangle au point C et au nouveau point cible dans la deuxième tranche de temps pour calculer un nouveau vt, puis entrez la troisième tranche de temps et répétez cette opération.

Supposons que les coordonnées initiales du missile et de la cible sont respectivement (x1, y1), (x, y), et construisons un triangle rectangle ABE. Ce triangle est utilisé pour trouver les valeurs sinusoïdales et cosinusoïdales de ∠. a, parce que vt est défini par vous-même, nous devons calculer de combien les coordonnées x et y du point A ont bougé respectivement. La valeur du mouvement est la longueur de AD et CD. Ces deux peuvent être multipliées par vt cos(a. ) et sin(a) respectivement.

Calculez sin(a) et cos(a), sinus par rapport à la pente, cosinus adjacent à la pente, l'hypoténuse peut être calculée à l'aide de la formule de distance en deux points, c'est-à-dire :

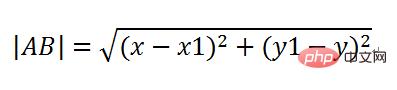
Ensuite, la longueur de

AC est la vitesse du missile qui est multipliée par le temps, qui est |AC|=vt, puis les longueurs de AD et CD peuvent être calculées. Ainsi, une fois cette tranche de temps écoulée, le missile devrait apparaître à la nouvelle position C. , et ses coordonnées sont l'ancien point A. x augmente AD et y moins CD.

Donc, les nouvelles coordonnées du point C sont :

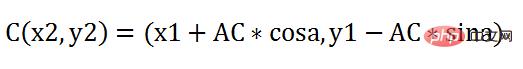
Continuez simplement à répéter cette opération à plusieurs reprises. Eh bien, pour la rendre plus vivante, assemblons la première tranche temporelle et la deuxième tranche temporelle :

.

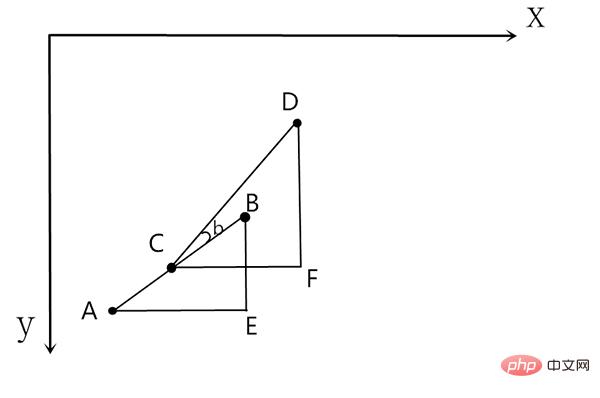
Le premier triangle construit par la tranche de temps est ABE. Après une tranche de temps, la cible marche du point B au point D. Le missile est au point C à ce moment, donc un nouveau triangle CDF est construit et répété. d'accord

D'accord, depuis que j'utilise la bibliothèque pygame de Python pour créer des petits jeux récemment, nous utiliserons pygame pour démontrer cet effet. L'effet est le suivant :

Le code très simple est le suivant :

import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()

.

Si seulement si le missile est considéré comme une particule, alors l'algorithme ci-dessus suffit. Je n'ai pas fait la rotation du missile, car une particule n'a pas besoin de tourner, qu'elle soit tête ou queue. Bien sûr, cela présuppose. que l'image du missile que vous chargez ne tourne pas lorsqu'elle est très petite. Cela ne semble pas poser de problème. Mais faire une rotation dans pygame n'est pas une tâche facile. Remplaçons d'abord l'image par un rectangle, puis ajoutons la fonction de rotation pour voir l'effet

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-
missile.get_height()/2))

car le point de coordonnées de l'image est son coin supérieur gauche, donc si nous voulons que les coordonnées de l'image soient fixées à la pointe de la flèche, réduisez simplement la position d'impression réelle x de l'image en réduisant la longueur de l'image et y en réduisant la largeur de moitié. Mais l'effet opérationnel réel n'est pas bon :

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢。经过一番研究，我发现原来是这个图旋转的机制问题，我们看看旋转后的图片变成什么样了：

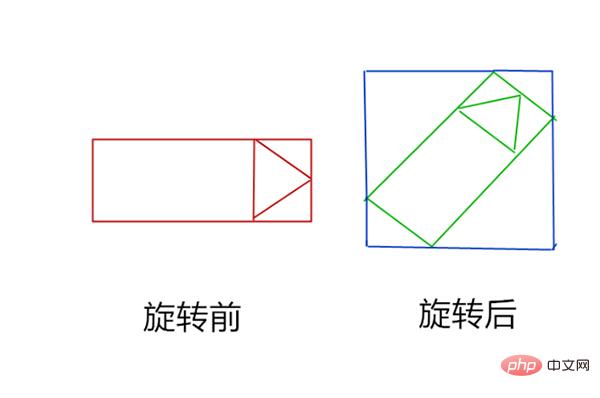
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，我们看旋转90的情况

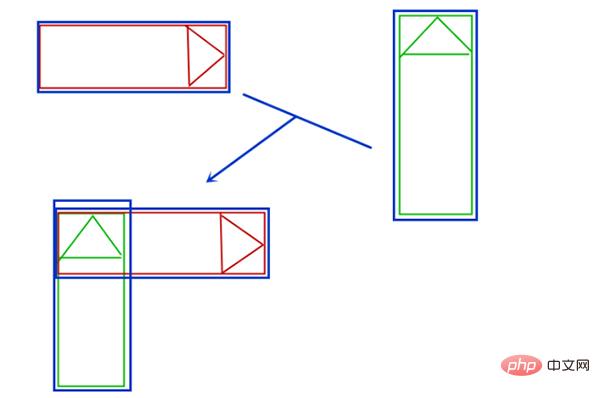
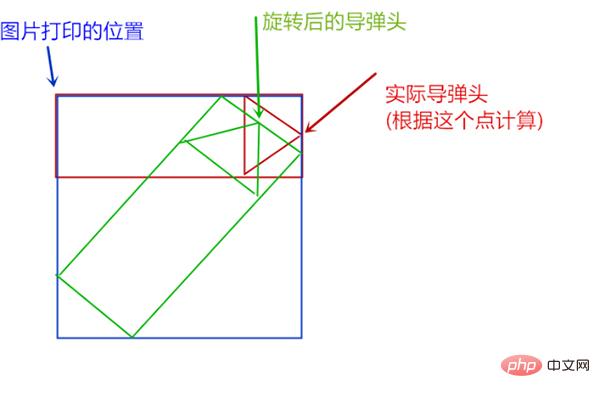
我们发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下，下，x，y分别移动两个头的距离，就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置，移动后应该是这样的：

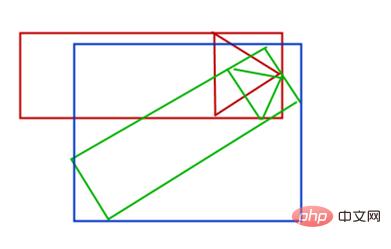
这样，两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以我们分为这四种情况

1，2象限

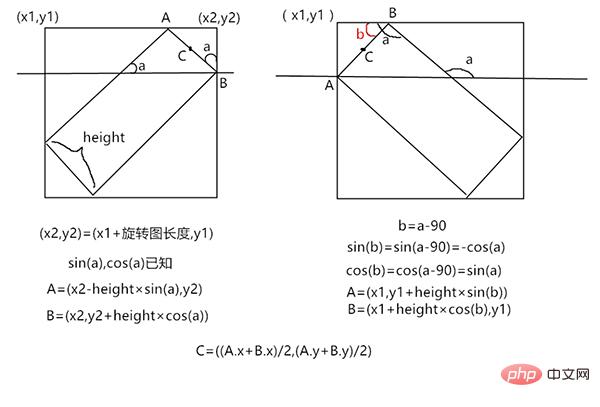
3，4象限，它的旋转只有正负0—180，所以3，4象限就是负角

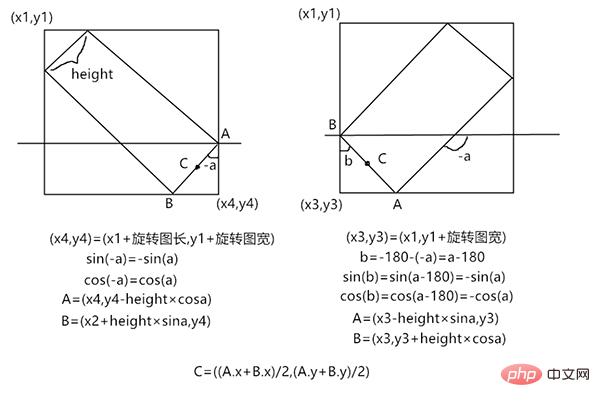
显示图片的时候我们将他移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)

所以最后我们加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()

以上便是用Python模拟导弹自动追踪的代码实例。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!