 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Résumé des principales idées techniques et méthodes d'inférence causale
Résumé des principales idées techniques et méthodes d'inférence causale
Résumé des principales idées techniques et méthodes d'inférence causale

Introduction : L'inférence causale est une branche importante de la science des données. Elle joue un rôle important dans l'itération des produits, l'évaluation des algorithmes et des stratégies d'incitation dans les milieux Internet et industriels. Elle est combinée avec des données, des expériences ou des modèles économétriques statistiques. Le calcul des avantages des nouveaux changements constitue la base de la prise de décision. Cependant, l’inférence causale n’est pas une question simple. Premièrement, dans la vie quotidienne, les gens confondent souvent corrélation et causalité. La corrélation signifie souvent que deux variables ont tendance à augmenter ou à diminuer en même temps, mais la causalité signifie que nous voulons savoir ce qui se passera lorsque nous modifions une variable, ou que nous nous attendons à obtenir un résultat contrefactuel si nous l'avons fait dans le même temps. passé Si nous prenons des mesures différentes, y aura-t-il des changements dans le futur ? La difficulté réside toutefois dans le fait que les données contrefactuelles sont souvent difficiles à observer et à collecter dans le monde réel.
Cet articlepasse en revue les principales idées et méthodes techniques des deux écoles d'inférence causale - le modèle causal de Rubin (RCM ; Rubin 1978) et le diagramme causal (Pearl 1995), ainsi que les développements récents dans Nouvelles méthodes et applications. Étant donné que la formation universitaire de l'auteur est relativement liée à l'économétrie, les méthodes et les articles cités se réfèrent principalement à la littérature économique. Il peut y avoir des omissions dans la profondeur et l'étendue de la théorie et de l'application de certaines méthodes.
Modèle de résultat potentiel
Nous utilisons i pour représenter chaque objet de recherche ou utilisateur, qui peut recevoir certaines interventions stratégiques : Ti=1représente l'intervention (groupe expérimental), Ti=0 ne représente aucune intervention ( groupe de référence), et les résultats correspondants qui nous intéressent sont respectivement Yi0 et Yi1, mais une seule situation se produira réellement, c'est-à-dire Yi0 et Yi1 un seul d'entre eux peut être observé, l'autre est inconnu. Le résultat de l'inférence causale que nous attendons ici est l'effet moyen du traitement ATE=E[Y1-Y0].
Nous pouvons expliquer la difficulté d'estimer l'ATE grâce à certaines dérivations mathématiques. Puisque nous n'observerons qu'un seul des Yi0 et Yi1, ce que nous pouvons directement calculer est en fait la différence inter-groupe E[Y entre le groupe expérimental et le groupe de base. i1 | ti = 1] -e [yi0 | cette différence peut être améliorée, le démontage est égal à E [yi1 |Ti=1]-E[Yi0|Ti=1] +E [Yi0 |T i=1]-E[Yi0|Ti=0]. Parmi eux, E[Yi1|Ti=1]-E[Yi0|Ti=1] le groupe expérimental individuel L'effet moyen du traitement (ATT) sur le test, ATT et ATE ne sont souvent pas égaux, et la différence entre les deux représente la validité externe (Validité Externe) que nous avons calculée. Si l'échantillon est limité aux utilisateurs d'un certain groupe d'âge, les résultats peuvent ne pas être généralisables aux utilisateurs de tous les groupes d'âge, ce qui indique que notre analyse peut ne pas avoir de validité externe. La deuxième partie de la formule ci-dessus est E[Yi0|Ti=1] -E[Yi0|Ti = 0] représente le biais de sélectivité de l'échantillon. Le biais de sélection peut souvent ne pas être nul dans la vie réelle. Par exemple, si le groupe expérimental et le groupe de référence ne sont pas échantillonnés de manière aléatoire et qu'il y aura des différences dans certaines distributions de caractéristiques, un biais de sélection peut alors se produire. Par conséquent, la différence entre les groupes que nous calculons représente en réalité l’effet de traitement moyen que nous attendons uniquement lorsque le biais de sélection est éliminé, a une validité externe et est basé sur un échantillon large et suffisant. La méthode de réflexion du modèle à effet potentiel consiste en fait à atteindre de telles conditions à travers certains paramètres et modèles. Derrière ses idées se cachent également des hypothèses mathématiques relativement strictes. Ci-dessous, nous passons en revue les idées principales ainsi que le développement technologique et les applications de ces dernières années selon différentes méthodes. En raison de contraintes d'espace, la méthode de régression par points d'arrêt ne sera pas présentée en détail ici. 1. Tests A/B
La méthode la plus courante de modèle d'effet potentiel est l'expérience randomisée, ou test A/B, que nous utilisons couramment dans l'industrie. Nous avons construit le groupe expérimental et le groupe de base grâce à un certain échantillonnage aléatoire pour observer les différences entre les groupes. Cependant, il convient de souligner que même si le caractère aléatoire est satisfait, l'efficacité de l'inférence causale doit encore ici répondre à une hypothèse importante : l'hypothèse de valeur de traitement unitaire stable (SUTVA). Les résultats potentiels de chaque individu ne concernent que lui-même et n'ont rien à voir avec l'intervention éventuelle d'autres individus par la stratégie expérimentale. Dans le même temps, l'intervention stratégique unique qui nous préoccupe n'a pas de formes ou d'intensités différentes qui conduisent à cela. différents résultats potentiels. Dans la vie réelle, il existe de nombreux scénarios dans lesquels les hypothèses du SUTVA ne sont pas respectées, ce qui a également inspiré le développement de diverses nouvelles techniques de tests A/B, telles que le contrôle budgétaire ou stratégique des problèmes d'encombrement, ou l'amélioration de la conception des détournements. Nous donnons ici quelques exemples liés au détournement :Chez LinkedIn, les expérimentateurs utilisent des méthodes expérimentales d'échantillonnage de réseau pour relever les défis que les réseaux sociaux posent aux expériences aléatoires individuelles traditionnelles. Premièrement, les utilisateurs sont divisés en différents groupes, et chaque groupe est utilisé individuellement pour distribuer et mesurer de manière aléatoire les indicateurs expérimentaux. L'effet estimé du traitement est corrigé en estimant l'exposition de l'utilisateur à l'effet de réseau (Gui et al. 2015).
Sur les plateformes comme Airbnb, il existe souvent une influence mutuelle entre acheteurs et vendeurs, qui peut également interférer avec les méthodes expérimentales traditionnelles. Les chercheurs construisent des indicateurs d’évaluation expérimentaux grâce à une conception expérimentale bilatérale et à des modèles dynamiques d’inventaires (Johari et al. 2022). Il convient de souligner que les expériences bilatérales constituent un domaine relativement nouveau et que leur conception expérimentale peut aider les expérimentateurs à découvrir les effets d’entraînement des expériences unilatérales traditionnelles. Cependant, il est difficile de faire des inférences statistiques et des corrections pour les résultats expérimentaux, et il se peut qu’il n’y en ait pas. une réponse absolue. Elle devrait être discutée davantage en combinaison avec des scénarios commerciaux.

Photos de l'article Johari et al. (2022)
2, Méthode des variables instrumentales
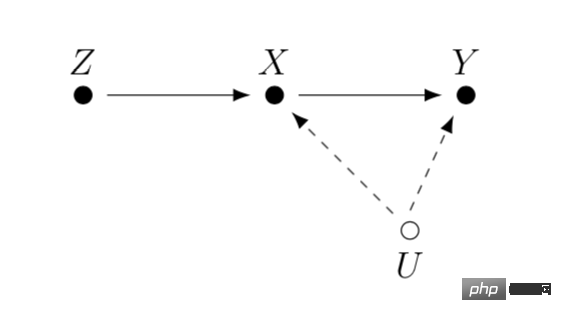
Les variables instrumentales sont une méthode pour résoudre l'en dogénéité des problèmes de régression linéaire . Ensuite, nous introduisons le problème de l'endogénéité et comment résoudre l'endogénéité à l'aide de variables instrumentales. Le principal problème de l’endogénéité est que nous nous soucions de l’effet de X sur Y, mais qu’il existe une variable U non mesurée qui affecte à la fois X et Y. Alors X est endogène et U est la variable de confusion mentionnée ci-dessus. Si nous pouvons trouver une variable Z liée à X et que Z n’est pas liée à U. Nous pouvons alors utiliser Z comme variable instrumentale pour estimer l’effet causal de X sur Y. La méthode de calcul spécifique est généralement la méthode des moindres carrés en deux étapes. Lorsque la méthode des variables instrumentales est effectivement utilisée, il convient de veiller à éviter le problème des « variables instrumentales faibles », c'est-à-dire que la corrélation entre la variable instrumentale Z et la variable d'intérêt X est très faible, ce qui entraînerait un biais dans la effet causal estimé. Vous pouvez vous fier à des méthodes de tests statistiques pour confirmer si un tel problème existe.

Un développement de la méthode des variables instrumentales consiste à la combiner avec un modèle d'apprentissage profond, comme la méthode Deep IV proposée par Hartford et al. Cette recherche transforme la méthode traditionnelle des moindres carrés en deux étapes des variables instrumentales en une tâche de prédiction plus flexible de deux réseaux neuronaux profonds, assouplissant les hypothèses fortes sur le processus de génération de données (DGP) de la méthode traditionnelle.
Dans des applications réelles, sur la base des scénarios accumulés à partir d'un grand nombre de tests A/B sur Internet, nous pouvons apprendre la relation causale entre les indicateurs grâce à des méthodes expérimentales de méta-apprentissage et de variables instrumentales. Par exemple, Peysakhovich & Eckles (2018) ont utilisé les données de Facebook, les informations du groupe expérimental comme variable instrumentale et ont combiné la régularisation L0 sur la base de la méthode des moindres carrés en deux étapes, ce qui peut résoudre le problème de biais de la variable instrumentale traditionnelle. méthode sur des échantillons limités, et peut également surmonter le problème des valeurs absolues d'effets relativement faibles (« variables instrumentales faibles ») observées dans un grand nombre d'expériences dans des situations du monde réel.
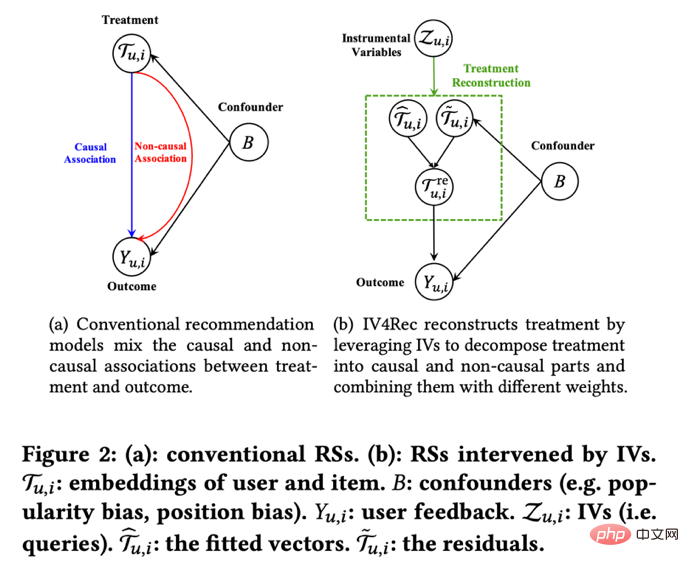
En plus d'apprendre la relation d'influence entre les indicateurs, l'idée devariables instrumentales peut également être utilisée pour résoudre le problème de biais dans les systèmes de recommandation. Dans les systèmes de recommandation, la formation des modèles s'appuie souvent sur les vues historiques des utilisateurs et les comportements de retour des likes, mais ces données historiques sont souvent affectées par des facteurs de confusion tels que l'emplacement d'affichage et le mode d'exposition. Chercheurs de Kuaishou et de l'Université Renmin Si et al. a proposé le cadre IV4Rec en utilisant l'idée de variables instrumentales, en utilisant la requête de recherche comme variable instrumentale pour décomposer les relations causales et non causales dans l'intégration du système de recommandation. Combiné avec l'apprentissage en profondeur, il peut être utilisé à la fois sur les données Kuaishou et. l’ensemble de données publiques MIND Vérifier l’effet de l’amélioration du modèle de recommandation.

Photos du journal Si et al.3. Méthode d'appariement
L'appariement est une méthode d'analyse causale largement utilisée par les entreprises, principalement pour résoudre le problème lorsque le groupe expérimental et le groupe témoin sont incomparables pour une raison quelconque (confondeur), en faisant correspondre chaque utilisateur. dans le groupe expérimental avec l'utilisateur du groupe témoin qui lui ressemble le plus dans certaines caractéristiques (appariement à gros grains CEM) ou qui a la probabilité la plus similaire de recevoir une intervention (score de propension) (appariement du score de propension PSM), pour recréer des groupe expérimental et groupe témoin. L'appariement est la méthode la plus similaire à l'expérience aléatoire AB/RCT (essai contrôlé randomisé). La méthode de fonctionnement est relativement similaire et les résultats sont très intuitifs. De plus, l’appariement est une méthode non paramétrique d’estimation des effets du traitement et n’est pas soumis aux hypothèses générales du modèle paramétrique linéaire. En faisant correspondre les échantillons, la méthode de la double différence peut également être utilisée, qui est souvent utilisée pour résoudre le problème du faible taux de pénétration des nouvelles fonctions. Ces dernières années, le développement de méthodes d'appariement a été principalement combiné avec des modèles d'apprentissage automatique pour rendre l'appariement des scores de propension plus précis. Dans le même temps, les idées présentées ici ont également été appliquées à d'autres méthodes causales et corrections de modèles d'apprentissage automatique. sera discuté plus tard.
4. Méthodes sérielles et développement des données de panel
Ces dernières années, de nombreuses nouvelles méthodes ont vu le jour autour de l'inférence causale des données de panel. Passons d’abord en revue les méthodes traditionnelles de données de panel.
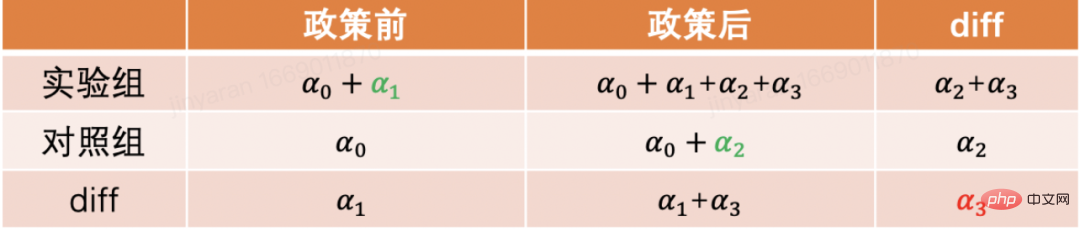
La méthode la plus couramment utilisée est la méthode de la double différence. La différence la plus simple consiste à contrôler la différence entre les groupes et à utiliser la forme d'un modèle de régression pour décrire yit=α0+α1Treati+α2 Postt+α 3Treati*Postt. Ici, Treati=1 représente si l'individu a été intervenu, et Postt=1 représente la période d'observation après l'intervention. Dans le tableau ci-dessous, nous pouvons constater que α2+α3 est la valeur de différence du groupe expérimental avant et après la date de l'expérience, α2 est la valeur de différence du groupe témoin avant et après la valeur de différence de date d'expérience. Par différence entre ces deux éléments, α3 est l'estimation de l'effet causal, qui est également le coefficient du terme d'interaction dans le modèle ci-dessus, et est le résultat de deux différences.

La méthode de différence en différence repose sur des hypothèses plus strictes. La « tendance parallèle » est la prémisse la plus importante, c'est-à-dire que les valeurs moyennes des indicateurs de résultats du groupe expérimental et du groupe de référence avant l'intervention politique sont stables dans le temps. Cela indique que l'impact d'autres facteurs que la politique. L'intervention elle-même est la même pour le groupe expérimental et le groupe de référence. Nous pouvons utiliser des graphiques de tendances temporelles pour tester des hypothèses parallèles, et certains logiciels d'inférence statistique fournissent également des fonctions correspondantes. Lorsque le test parallèle échoue, des tests supplémentaires peuvent être effectués en ajoutant des variables de contrôle ou des termes de tendance temporelle à la régression. Dans certains cas, ce problème peut également être résolu à l’aide de la méthode des triples différences. De plus, dans la pratique réelle, il existe de nombreuses façons de mettre en œuvre la méthode de la double différence. En plus de la méthode mentionnée ci-dessus, le paramètre "modèle à effets fixes bidirectionnel" Yit=τTreatit+Xitβ+αi+ξt+ε it , Mais cela repose également sur des hypothèses fortes : il n'y a pas de facteurs de confusion qui changent avec le temps, et les résultats passés n'affecteront pas l'état actuel du traitement. Cela nécessite également que l'effet thérapeutique de la politique reste inchangé. Concernant les limites de la théorie et des méthodes qui la sous-tendent, ainsi que les nouvelles méthodes élargies telles que l'appariement et la repondération, il est recommandé d'étudier en combinaison avec les cours dispensés par le professeur Xu Yiqing de l'Université de Stanford :
https://yiqingxu.org/teaching /
Ci-dessous, nous énumérons certaines des nouvelles méthodes les plus couramment utilisées :
La méthode de contrôle synthétique est un ensemble de méthodes dérivées de la méthode d'inférence causale des données de panel, et de nouvelles recherches sur les tests d'estimation ou d'inférence statistique émergent constamment. Lorsque l'intervention est mise en œuvre dans un groupe ou une région, le groupe expérimental n'a qu'une seule valeur d'observation à un moment donné et la période de temps des données est longue, comme une ville menant des activités de promotion locale, généralement la différence de La méthode de différence ne convient pas pour le moment, des méthodes de contrôle synthétiques peuvent être adoptées. Le principe est de sélectionner certaines villes témoins et de les intégrer dans un « groupe témoin virtuel » très similaire au groupe expérimental avant l'intervention. Pour une introduction théorique détaillée et une optimisation ces dernières années, veuillez vous référer au professeur Aberto Abadie du Massachusetts Institute. of Technology et ses collaborateurs (Abadie, Diamond et Hainmueller 2010) et son cours de courte durée au NBER pour poursuivre ses études :
https://www.nber.org/lecture/2021-summer-institute- méthodes-conférence-alberto-abadie-contrôles-synthétiques-méthodes-et-pratique
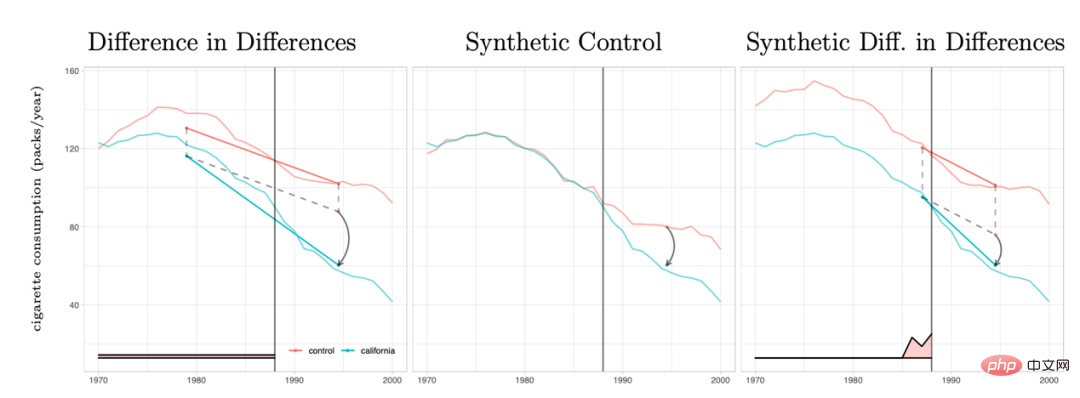
La méthode de la double différence et la méthode de contrôle synthétique peuvent en fait être unifiées au sein d'un système de cadre analytique. Les recherches d'Arkhangelsky et al. (2021) ont souligné que la différence dans les différences résout un problème de régression bidirectionnelle à effets fixes sans aucune pondération individuelle ou temporelle, tandis que la méthode de contrôle synthétique applique des poids ω aux individus avant que l'intervention politique ne se produise pour s'adapter. l'intervention. Le poids du temps λ peut ici être compris comme la période de données qui est la plus similaire à la période après l'intervention reçoit un poids plus élevé.


Comparaison de plusieurs méthodes : L'image est tirée de l'article Arkhangelsky et al (2021)
Les données de panel peuvent également être combinées avec la méthode de complétion matricielle pour l'inférence causale. , ce qui constitue également un nouveau développement dans ce domaine ces dernières années. L'algorithme de complétion matricielle résout le problème des données contrefactuelles manquantes rencontrées par l'inférence causale en résolvant un problème d'optimisation convexe. Cette méthode convient aux situations dans lesquelles les individus sont soumis à des délais d'intervention de stratégie incohérents. Par exemple, une itération d'un produit nécessite que les utilisateurs mettent à jour la version du produit pour prendre effet, mais les délais de mise à jour des utilisateurs sont incohérents. Pour une théorie détaillée de la méthode, veuillez vous référer à des articles connexes tels que Athey et al. Les méthodes de complétion matricielle, de contrôle synthétique et de prédiction de régression sous intervention aléatoire peuvent également être unifiées dans le cadre de problèmes d'optimisation, et nous pouvons également combiner plusieurs méthodes de manière globale pour obtenir des résultats d'estimation plus robustes (Athey et.al 2019) .

Schéma de principe de complétion matricielle : L'image provient du cours de Guidon Imbens à l'AEA, où W représente l'état du traitement https://www.aeaweb.org/conference/cont-ed/2018- webcasts
Dans cette section, nous avons présenté les principales méthodes et progrès de l'inférence causale sur données de panel. Ce domaine est un domaine avec des méthodes très diverses et des progrès très rapides, mais il nécessite que les utilisateurs réfléchissent pleinement aux raisons qui les sous-tendent. Les hypothèses et les limites peuvent être utilisées pour évaluer plus précisément diverses politiques dans la pratique. En raison du manque de place, nous ne donnons ici qu’une très brève introduction.
5. Un examen des méthodes pour les effets causals hétérogènes
La combinaison de méthodes d'apprentissage automatique pour étudier les effets causals hétérogènes est en fait une tendance dans le développement de l'inférence causale ces dernières années. Introduisons d'abord l'effet causal hétérogène : l'effet de traitement hétérogène (HTE) fait référence au phénomène selon lequel les expériences produisent des effets différents sur les individus en raison de différentes caractéristiques individuelles des échantillons. Exprimé en combinaison avec des formules mathématiques, le HTE revêt de nombreuses formes :
L'effet causal ITE (effet de traitement individuel) de chaque individu : τi=Yi1-Yi0, un seul de Yi1 et Yi0 peut être observé, l'autre et τ i doit être estimé par une certaine méthode de modèle.
L'effet causal moyen du groupe sur certaines caractéristiques. Nous utilisons ici l'Effet : τ(x)=E[Y1-Y0|X=x].
La méthode d’analyse de HTE propose actuellement un large éventail de scénarios d’application. Grâce à HTE, nous pouvons connaître les caractéristiques des groupes qui répondent le plus à une certaine intervention stratégique. Cela peut également nous aider à étudier le mécanisme d'une stratégie de test A/B qui a l'effet attendu ou n'a aucun effet. appliqué à diverses personnalisations parmi les stratégies. Les méthodes d'inférence causale hétérogène ont de nombreuses applications dans l'industrie et sur Internet. Par exemple, TripAdvisor est utilisé pour mesurer les incitations à l'inscription des membres et Microsoft utilise cette méthode et des données à court terme pour mesurer le retour sur investissement à long terme de différents projets. trouvé Reportez-vous au cours de formation KDD 2021 (https://causal-machine-learning.github.io/kdd2021-tutorial/).
La méthode la plus courante pour les effets causals hétérogènes est en fait l'analyse multidimensionnelle couramment utilisée en analyse expérimentale. Cependant, l'utilisation de l'analyse multidimensionnelle doit se méfier du problème des tests multiples. Dans le même temps, lorsqu'il y a suffisamment de dimensions, les exigences en matière de taille de l'échantillon expérimental sont relativement élevées et l'efficacité de l'analyse est relativement faible. La méthode d'apprentissage automatique fournit des méthodes d'exploration qui améliorent l'efficacité. Son avantage est qu'elle peut apprendre de manière adaptative la distribution des effets causals hétérogènes et ne nécessite pas d'hypothèses de forme fonctionnelle strictes. Elle est meilleure que les méthodes économétriques traditionnelles basées sur la régression linéaire ou l'analyse multidimensionnelle. les méthodes ont des degrés de liberté plus élevés, mais le défi technique consiste à savoir comment faire des inférences statistiques. Ces dernières années, avec l'approfondissement de la combinaison de l'apprentissage automatique et de l'économétrie, de nombreux ensembles de méthodes ont été innovés et appliqués dans ce domaine. Nous nous concentrons ici sur les types de méthodes suivants. Les hypothèses de base de ces méthodes sont des hypothèses d'indépendance conditionnelle (. Hypothèse d’indépendance conditionnelle), c’est-à-dire que ce n’est que lorsque diverses variables confondantes sont suffisamment contrôlées que nous pouvons obtenir des estimations relativement précises des effets causals.
Forêt causale : Basée sur une forêt aléatoire, il s'agit d'une méthode non paramétrique qui effectue directement une estimation d'ajustement. La principale logique d’estimation d’un arbre causal est de définir la fonction de perte de l’arbre global en définissant l’effet causal sur chaque feuille. L'arbre causal vise à maximiser la somme des pertes de toutes les feuilles selon une certaine manière de diviser X. Outre les différents objectifs d'estimation des algorithmes d'arbres dans l'apprentissage automatique, une autre différence est que dans les algorithmes d'inférence causale, les échantillons d'ensembles d'apprentissage sont généralement divisés en ensembles d'apprentissage et en ensembles d'estimation. L'ensemble d'apprentissage est utilisé pour le partitionnement des feuilles et l'ensemble d'estimation est utilisé. utilisé Calculer l’effet moyen du traitement sur chaque nœud foliaire après le feuillage. L'avantage de l'arbre causal est que les résultats sont très concis et faciles à comprendre. Vous pouvez identifier directement les groupes de personnes présentant des différences claires dans les effets expérimentaux grâce au regroupement. Le premier indicateur regroupé est souvent la plus grande dimension de la différence dans les effets causals. . Cependant, les arbres causals sont sujets au surajustement. Dans les travaux pratiques, il est recommandé d'utiliser des forêts aléatoires causales (pour plus de détails, veuillez vous référer à Athey et Imbens 2016, Wager et Athey 2018. Dans le même temps, les forêts causales aléatoires ont également de meilleurs résultats). propriétés d'inférence statistique. Pour l'expansion de cette méthode, veuillez vous référer aux travaux de recherche tels que Athey, Tibshirani et Wager (2019) et Friedberg et al (2020). Ces nouvelles méthodes peuvent traiter davantage les problèmes lorsqu'il existe des variables confondantes et estimer les résultats de manière plus fluide. .
Meta Learners : est différent des modèles qui utilisent des arbres causals pour estimer directement les effets causals. Il s'agit d'un type de modèle d'estimation indirecte : il modélise directement la variable de résultat Y. Par conséquent, Meta Learner ne peut pas utiliser directement l'HTE estimé pour l'inférence statistique. Dans des applications pratiques, certains chercheurs utiliseront des méthodes bootstrap pour résoudre ce problème. Il existe trois types d'algorithmes d'estimation des Meta Learners : T-Learner, S-Learner et X-Learner. La différence fondamentale entre les trois méthodes est la suivante :
La plus simple est S-learner. Il utilise la variable intermédiaire comme variable caractéristique pour la modélisation ponctuelle, ce qui convient aux situations où les variables de traitement et de résultat sont fortement corrélées, sinon le modèle ne peut pas identifier le changement du résultat causé par les changements de la variable intermédiaire
;Le plus compliqué est T-learner. Il identifie les effets causals en forçant deux modèles à apprendre respectivement Yi1 du groupe expérimental et Yi0 du groupe témoin. Il peut être utilisé lorsque les valeurs d'observation variables du groupe expérimental et du groupe témoin sont plus élevées. et plus moyen, sinon l'un d'eux Le modèle sera plus régularisé
X-learner est une méthode relativement nouvelle en utilisant une estimation en deux étapes et une correction du score de propension, il peut faire des comparaisons avec une petite quantité de. données Bonne estimation (voir Künzel et al. 2019 pour plus de détails).
Cadre d'estimation basé sur DML et DRL : Nous introduisons ces deux cadres en combinaison avec l'outil Econml de Microsoft :
https://www.microsoft.com/en-us /research /project/econml/
DML (double machine learning) est un cadre qui confond de manière flexible les variables et traite la relation entre les variables et les variables de résultat lorsque des variables confondantes de grande dimension existent. principalement divisé en deux étapes lors de l'estimation de l'effet causal : la première étape consiste à utiliser deux modèles d'apprentissage automatique (pas nécessairement les mêmes) pour estimer E(Y|X,W) et E(T| X, W) deux attentes conditionnelles, puis prenez le résidu. Ici, X et W sont des variables confusionnelles, mais seul X est la variable pertinente dans CATE. La deuxième étape consiste à estimer ATE ou CATE sur la base du résidu. Lors de l'estimation de CATE, le résidu de T-E(T|X,W) est multiplié par une fonction θ(X) autour de X pour l'estimation. Pour plus d’informations sur la façon d’estimer l’ATE, veuillez consulter Chernozhukov et al. Econml propose de nombreux modèles parmi lesquels choisir dans la deuxième étape : LinearDML (en utilisant le modèle OLS), DML (en utilisant un modèle personnalisé), CausalForestDML (en utilisant une forêt aléatoire causale)... Lorsque vous utilisez le framework DML, vous devez veiller à vérifier si les moyennes des termes résiduels des deux modèles sont significativement différentes de 0 ou significativement corrélées. Si tel est le cas, cela signifie que les variables confondantes ne sont peut-être pas suffisamment contrôlées.
Le framework DRL est basé sur la méthode Doublement Robuste, qui est également divisée en deux étapes. La première étape utilise X, W, T pour prédire Y et définit la valeur prédite comme gt. (X, W); La deuxième étape utilise un modèle de classification pour prédire T en utilisant Il convient de noter que T ici est une variable discrète et restreint gt(X,W) à une sorte de modèle basé sur la régression. Après le résultat en deux étapes, une variable de résultat ajustée est calculée :
Ensuite, le Y
i,tDR ajusté est dans le groupe expérimental et le contrôle Regroupez la différence Yi1DR-Yi0DR, et renvoyez X pour obtenir CATE. La raison pour laquelle DRL est appelé Doublement Robuste est que dans la formule ci-dessus, tant que l'un des gt(X,W) et pt(X,W) est correct, l'effet causal sera estimé. Il est impartial. Mais si les deux estimations du modèle sont fausses, l’erreur qui en résulte peut être très importante. Semblable au DML, la différence entre les différents apprenants de DRL dans Econml réside dans le type de modèle utilisé pour adapter Y avec .
Le plus grand défi d'application des méthodes d'inférence causale hétérogène basées sur des modèles d'apprentissage automatique est en fait de savoir comment sélectionner un modèle d'apprentissage automatique approprié et ajuster les paramètres pour obtenir des résultats d'estimation relativement robustes. Sur la base de l'expérience d'application et des recherches récentes, les précautions suivantes doivent être prises :
- Assurez-vous que la taille de l'échantillon de formation est suffisamment grande.
-
Si vous utilisez l'outil Econml, il est recommandé d'utiliser la fonction score* pour sélectionner le modèle (plus le score est petit, meilleur est le modèle), mais tous les modèles n'ont pas cette fonction : par exemple, DML l'a mais pas X-Learner ou Causal Forest. Si vous utilisez Causalml d'Uber, vous pouvez utiliser le graphique de gain cumulatif pour comparer les performances de différents méta-apprenants.
https://github.com/uber/causalml.
- Certaines méthodes peuvent effectuer des tests statistiques sur HTE, mais d'autres ne le peuvent pas. Dans Econml, les méthodes qui peuvent être utilisées pour effectuer des tests statistiques sur HTE sont limitées à la méthode dans laquelle la dernière étape du modèle dans DML/DRL est définie sur un modèle linéaire ou une forêt causale, tandis que la variable de caractéristique X et la Les variables expérimentales T sont liées de manière non linéaire dans de nombreux scénarios commerciaux. Le choix forcé d'un modèle linéaire peut entraîner un biais d'estimation de HTE (par exemple, la volatilité de HTE n'a rien à voir avec X et n'est que du bruit). Si des individus présentant une HTE significative doivent être dépistés pour une analyse ultérieure, une correction de tests multiples pour les tests d'effets individuels est nécessaire.
- En plus du degré d'ajustement du modèle, une norme est également nécessaire pour mesurer la qualité de l'estimation HTE : par exemple, si la variation de HTE est suffisamment importante pour distinguer les groupes sensibles des groupes non sensibles, vous peut se référer à la méthode proposée par Chernozhukov et al. (2018). L'inférence statistique basée sur les caractéristiques HTE est également très facile à appliquer.
Les méthodes présentées ci-dessus se concentrent essentiellement sur l'effet causal hétérogène statique sous une variable intermédiaire. Mais dans les applications pratiques, les problèmes que nous rencontrerons seront plus complexes. Par exemple, de multiples variables intervenantes sont impliquées : les incitations en matière de subventions fournies par le produit aux utilisateurs peuvent inclure à la fois des incitations à la connexion et des récompenses pour d'autres tâches. La manière d'équilibrer la répartition des différents types d'incitations peut être définie comme une construction à effet causal hétérogène. de multiples variables intervenantes dans des problèmes de modélisation et d'optimisation. Un autre exemple est celui des effets causals dynamiques, dans lesquels les variables confusionnelles changent avec l'intervention à différents moments (voir Lewis et Syrgkanis 2020). Prenons l'exemple des tâches d'incitation. Ces tâches peuvent amener les utilisateurs à prêter attention à de nouvelles ancres, modifiant ainsi leurs préférences en matière de visualisation du contenu, et affecteront également l'effet des incitations ultérieures. Ces scénarios complexes ont inspiré l’expansion de diverses méthodes, et nous attendons également avec impatience l’émergence de recherches et d’applications plus établies et plus systématiques à l’avenir.
Modèle causal structurel
Dans la section précédente, nous avons présenté les idées principales et le développement méthodologique des modèles de résultats latents. Ce type de méthode scolaire a une théorie statistique relativement complète et peut obtenir des résultats d'estimation relativement précis. Cependant, il existe certaines limites. Il ne peut être utilisé que pour estimer l'influence d'un seul degré de corrélation entre les variables (c'est-à-dire qu'une seule variable dépendante et certaines variables indépendantes sont autorisées, et les liens d'effets indirects ne peuvent pas être estimés). la relation entre de nombreuses variables Les liens et les relations complexes nécessitent l'utilisation d'une autre école de méthodes de modèles causals structurels.
Le modèle causal structurel utilise un graphe acyclique dirigé (DAG) pour décrire la relation causale et la distribution conditionnelle entre les variables. Chaque nœud du graphe est une variable, et la relation causale est représentée par les arêtes reliant ces nœuds. Par exemple, X11, on appelle aussi X. 1 un nœud enfant, et Pour un DAG formé d'un ensemble de variables aléatoires X=(X1, P(X)=∏pj=1P( est X Le nœud parent immédiat de j. Lorsque nous exprimons la relation causale, nous introduisons le concept d'opérateur do, en supposant que le courant X=(X1, )=(x1,x2 ,...xp), utilisez do(Xj=x ' j) représente l'intervention pour la variable P(X1 =x1, p =xp|do(Xj=x 'j)) , le changement attendu de chaque variable selon l'ancienne et la nouvelle distribution est l'effet causal de sur elles, tel que E(X1|do)( 1|do(X j=xj)). Judea Pearl, la fondatrice du modèle causal des résultats, a souligné dans ses recherches que lors de l'utilisation de diagrammes de causalité pour identifier les relations causales, si le « critère de la porte dérobée » et le « critère de la porte d'entrée » sont remplis, il n'est pas réellement nécessaire d'observer toutes les variables. Concernant les détails spécifiques, veuillez vous référer à Pearl (2009) pour les détails théoriques. Il convient d’ajouter que le modèle causal structurel et le modèle de résultats potentiels sont en réalité liés. Dans les applications pratiques, nous ne disposons peut-être pas directement des informations nécessaires pour définir un graphe causal, donc comment apprendre la structure du graphe causal entre les variables est devenu une question importante. Lors de la résolution de ce type de problème, nous devons d'abord clarifier les hypothèses requises :
Hypothèse causale de Markov : Cette hypothèse signifie que la distribution conditionnelle de tout nœud est basée uniquement sur son nœud parent direct.
Hypothèse de suffisance causale : Cette hypothèse équivaut à l'absence de variables confondantes non observées.
Hypothèse de fidélité causale : Cette hypothèse signifie que, sur la base d'une distribution de probabilité conditionnelle, certains nœuds sont indépendants les uns des autres (le graphique peut donc être coupé).
Les algorithmes sont grossièrement divisés en deux catégories :
Pour une introduction détaillée, veuillez vous référer à Glymour, Zhang et Sprites (2019) et à l'article "Statistical Methods of Causal Inference" dans "Science China : Mathématiques" Numéro 12, 2018 》:
https://cosx.org/2022/10/causality-statistical-method/.
Algorithmes basés sur les contraintes : Apprenez tous les graphiques causals qui satisfont aux hypothèses de fidélité et de markov causal basées sur le test d'indépendance de la distribution conditionnelle, c'est-à-dire testez si la distribution conditionnelle entre deux nœuds est indépendante. Par exemple, l'algorithme PC (Spirtes et Glymour 1991) et l'algorithme IC (Verma et Pearl 1990).
Algorithmes basés sur les scores : Trouvez la structure graphique qui correspond le mieux aux données en optimisant un certain score défini. Les équations structurelles et les fonctions de score doivent être définies. Par exemple, l'algorithme CGNN (Goudet et al. 2017) et l'algorithme NOTEARS (Zheng et al. 2018). Ici, nous nous concentrons sur l'algorithme NOTEARS. L'algorithme traditionnel est basé sur tous les nœuds et les relations possibles entre les nœuds, recherchant dans tous les graphiques possibles et sélectionnant la solution optimale selon une certaine norme. Il s'agit d'un problème NP-difficile typique qui prend beaucoup de temps. Les ressources informatiques de longue date et actuelles sont fondamentalement incapables de répondre aux besoins informatiques. L'algorithme NOTEARS transforme le problème de recherche discrète en un problème de recherche continue. Cet algorithme améliore considérablement la vitesse de calcul et le rend utilisable par les analystes de données ordinaires. Cependant, cette méthode présente également certaines limites. Par exemple, on suppose que le bruit de toutes les variables doit être distribué de manière gaussienne. Ces dernières années, de plus en plus de méthodes (telles que He et al. 2021) ont tenté d'améliorer les hypothèses de. de telles méthodes.
Avec le développement du domaine de l'apprentissage par renforcement, nous avons également découvert que l'inférence causale et l'apprentissage par renforcement peuvent être combinés pour favoriser le développement de chacun. L'inférence causale peut aider les algorithmes d'apprentissage par renforcement à apprendre plus efficacement les fonctions de valeur ou les stratégies optimales en déduisant la relation causale entre les états ou entre les états et les actions dans l'apprentissage par renforcement. Les lecteurs intéressés par cet aspect peuvent se référer au professeur Elias Bareinboim des cours de l'Université de Columbia (. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). D'autre part, l'apprentissage par renforcement peut également être intégré à l'algorithme d'apprentissage des graphiques causals, comme Zhu, Ng et Chen (2019) du laboratoire Noah's Ark de Huawei.
Concernant les perspectives d'avenir de l'inférence causale, il convient de mentionner un nouveau paradigme de recherche lié à l'apprentissage des graphes, à l'inférence causale et à l'apprentissage automatique ces dernières années : il s'agit du concept « d'apprentissage stable » proposé par l'équipe du professeur Cui Peng. de l’Université Tsinghua (Cui et Athey 2022). L'application de modèles tels que l'apprentissage automatique et l'intelligence artificielle repose sur une hypothèse importante : l'hypothèse d'indépendance et de distribution identique. C'est-à-dire que l'ensemble de formation et l'ensemble de test doivent provenir de la même distribution, mais en fait, il existe divers problèmes OOD (Out Of Distribution, out of distribution). À l'heure actuelle, les performances du modèle ne peuvent pas être garanties. C'est aussi un problème auquel sont confrontés divers modèles dans l'histoire, un risque technique important. L’inférence causale peut aider à surmonter de tels problèmes. S'il peut être garanti qu'une structure a le même effet prédictif dans divers environnements pour résoudre le problème OOD, alors cette structure doit être une structure causale et les performances d'une structure causale dans divers environnements sont relativement stables. Les recherches menées par l'équipe de Cui Peng (He et al. 2022, Shen et al. 2021) ont révélé qu'en utilisant l'idée de confondre l'équilibre d'appariement des variables, toutes les variables peuvent être rendues indépendantes en repondérant l'échantillon, faisant ainsi d'un modèle basé sur la corrélation un modèle basé sur les causes et les effets. L'apprentissage dit stable consiste à utiliser un ensemble d'apprentissage d'une distribution et un ensemble de test de plusieurs distributions inconnues différentes. L'objectif d'optimisation est de minimiser la variance de précision. Je pense qu'il s'agit d'un domaine très important à l'avenir et que les lecteurs intéressés peuvent continuer à prêter attention aux progrès de la recherche pertinents.

Comparaison de l'apprentissage indépendant et distribué à l'identique, de l'apprentissage par transfert et de l'apprentissage stable : images de l'article Cui et Athey 2022
Dans les applications pratiques, les systèmes de recommandation, la vision par ordinateur, la conduite automatique , naturel L'inférence causale et l'apprentissage de graphes causals ne manquent pas dans les domaines liés à l'apprentissage automatique et à l'intelligence artificielle tels que le traitement du langage, ce qui a favorisé le développement de ces domaines. Nous énumérons également ici quelques exemples d'applications plus détaillées liées à ces dernières années. à l'apprentissage automatique. Pour les simulateurs de référence et les ensembles de données, veuillez vous référer au résumé des chercheurs de l'UCL et de l'Université d'Oxford (Kaddour et al. 2022). Dans le domaine des systèmes de recommandation, comme nous l'avons introduit dans l'application des méthodes de variables instrumentales, les systèmes de recommandation comportent inévitablement des biais. L'identification de la relation graphique causale entre les utilisateurs et les éléments peut aider le système de recommandation à corriger les biais. Par exemple, Wang et al. (2021) et Zhang et al. (2021) ont utilisé des diagrammes de causalité pour éliminer respectivement les biais causés par le clickbait et la popularité. Dans le domaine de la conduite autonome, des chercheurs de Microsoft ont lancé CausalCity (McDuff et al. 2022), une plateforme d'environnement de conduite simulée qui intègre l'inférence causale dans la prédiction de trajectoire des véhicules. Dans le domaine du traitement du langage naturel, les chercheurs ont découvert que l'inférence causale peut aider les méthodes de PNL à être plus robustes et compréhensibles (Zeng et al. 2020), notamment en testant les biais dans les modèles de langage et les corpus (Vig et al. 2020)... I Je crois qu'à l'avenir, l'inférence causale continuera à prospérer, jouant un rôle important dans ces domaines et dans d'autres.
3. Méthode d'appariement
L'appariement est une méthode d'analyse causale largement utilisée par les entreprises, principalement pour résoudre le problème lorsque le groupe expérimental et le groupe témoin sont incomparables pour une raison quelconque (confondeur), en faisant correspondre chaque utilisateur. dans le groupe expérimental avec l'utilisateur du groupe témoin qui lui ressemble le plus dans certaines caractéristiques (appariement à gros grains CEM) ou qui a la probabilité la plus similaire de recevoir une intervention (score de propension) (appariement du score de propension PSM), pour recréer des groupe expérimental et groupe témoin. L'appariement est la méthode la plus similaire à l'expérience aléatoire AB/RCT (essai contrôlé randomisé). La méthode de fonctionnement est relativement similaire et les résultats sont très intuitifs. De plus, l’appariement est une méthode non paramétrique d’estimation des effets du traitement et n’est pas soumis aux hypothèses générales du modèle paramétrique linéaire. En faisant correspondre les échantillons, la méthode de la double différence peut également être utilisée, qui est souvent utilisée pour résoudre le problème du faible taux de pénétration des nouvelles fonctions. Ces dernières années, le développement de méthodes d'appariement a été principalement combiné avec des modèles d'apprentissage automatique pour rendre l'appariement des scores de propension plus précis. Dans le même temps, les idées présentées ici ont également été appliquées à d'autres méthodes causales et corrections de modèles d'apprentissage automatique. sera discuté plus tard.
4. Méthodes sérielles et développement des données de panel
Ces dernières années, de nombreuses nouvelles méthodes ont vu le jour autour de l'inférence causale des données de panel. Passons d’abord en revue les méthodes traditionnelles de données de panel.
La méthode la plus couramment utilisée est la méthode de la double différence. La différence la plus simple consiste à contrôler la différence entre les groupes et à utiliser la forme d'un modèle de régression pour décrire yit=α0+α1Treati+α2 Postt+α 3Treati*Postt. Ici, Treati=1 représente si l'individu a été intervenu, et Postt=1 représente la période d'observation après l'intervention. Dans le tableau ci-dessous, nous pouvons constater que α2+α3 est la valeur de différence du groupe expérimental avant et après la date de l'expérience, α2 est la valeur de différence du groupe témoin avant et après la valeur de différence de date d'expérience. Par différence entre ces deux éléments, α3 est l'estimation de l'effet causal, qui est également le coefficient du terme d'interaction dans le modèle ci-dessus, et est le résultat de deux différences.
La méthode de différence en différence repose sur des hypothèses plus strictes. La « tendance parallèle » est la prémisse la plus importante, c'est-à-dire que les valeurs moyennes des indicateurs de résultats du groupe expérimental et du groupe de référence avant l'intervention politique sont stables dans le temps. Cela indique que l'impact d'autres facteurs que la politique. L'intervention elle-même est la même pour le groupe expérimental et le groupe de référence. Nous pouvons utiliser des graphiques de tendances temporelles pour tester des hypothèses parallèles, et certains logiciels d'inférence statistique fournissent également des fonctions correspondantes. Lorsque le test parallèle échoue, des tests supplémentaires peuvent être effectués en ajoutant des variables de contrôle ou des termes de tendance temporelle à la régression. Dans certains cas, ce problème peut également être résolu à l’aide de la méthode des triples différences. De plus, dans la pratique réelle, il existe de nombreuses façons de mettre en œuvre la méthode de la double différence. En plus de la méthode mentionnée ci-dessus, le paramètre "modèle à effets fixes bidirectionnel" Yit=τTreatit+Xitβ+αi+ξt+ε it , Mais cela repose également sur des hypothèses fortes : il n'y a pas de facteurs de confusion qui changent avec le temps, et les résultats passés n'affecteront pas l'état actuel du traitement. Cela nécessite également que l'effet thérapeutique de la politique reste inchangé. Concernant les limites de la théorie et des méthodes qui la sous-tendent, ainsi que les nouvelles méthodes élargies telles que l'appariement et la repondération, il est recommandé d'étudier en combinaison avec les cours dispensés par le professeur Xu Yiqing de l'Université de Stanford :
https://yiqingxu.org/teaching /
Ci-dessous, nous énumérons certaines des nouvelles méthodes les plus couramment utilisées :
La méthode de contrôle synthétique est un ensemble de méthodes dérivées de la méthode d'inférence causale des données de panel, et de nouvelles recherches sur les tests d'estimation ou d'inférence statistique émergent constamment. Lorsque l'intervention est mise en œuvre dans un groupe ou une région, le groupe expérimental n'a qu'une seule valeur d'observation à un moment donné et la période de temps des données est longue, comme une ville menant des activités de promotion locale, généralement la différence de La méthode de différence ne convient pas pour le moment, des méthodes de contrôle synthétiques peuvent être adoptées. Le principe est de sélectionner certaines villes témoins et de les intégrer dans un « groupe témoin virtuel » très similaire au groupe expérimental avant l'intervention. Pour une introduction théorique détaillée et une optimisation ces dernières années, veuillez vous référer au professeur Aberto Abadie du Massachusetts Institute. of Technology et ses collaborateurs (Abadie, Diamond et Hainmueller 2010) et son cours de courte durée au NBER pour poursuivre ses études :
https://www.nber.org/lecture/2021-summer-institute- méthodes-conférence-alberto-abadie-contrôles-synthétiques-méthodes-et-pratique
La méthode de la double différence et la méthode de contrôle synthétique peuvent en fait être unifiées au sein d'un système de cadre analytique. Les recherches d'Arkhangelsky et al. (2021) ont souligné que la différence dans les différences résout un problème de régression bidirectionnelle à effets fixes sans aucune pondération individuelle ou temporelle, tandis que la méthode de contrôle synthétique applique des poids ω aux individus avant que l'intervention politique ne se produise pour s'adapter. l'intervention. Le poids du temps λ peut ici être compris comme la période de données qui est la plus similaire à la période après l'intervention reçoit un poids plus élevé.
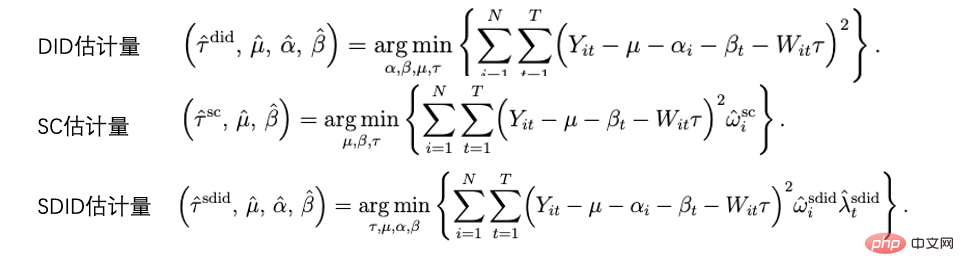
Comparaison de plusieurs méthodes : L'image est tirée de l'article Arkhangelsky et al (2021)
Les données de panel peuvent également être combinées avec la méthode de complétion matricielle pour l'inférence causale. , ce qui constitue également un nouveau développement dans ce domaine ces dernières années. L'algorithme de complétion matricielle résout le problème des données contrefactuelles manquantes rencontrées par l'inférence causale en résolvant un problème d'optimisation convexe. Cette méthode convient aux situations dans lesquelles les individus sont soumis à des délais d'intervention de stratégie incohérents. Par exemple, une itération d'un produit nécessite que les utilisateurs mettent à jour la version du produit pour prendre effet, mais les délais de mise à jour des utilisateurs sont incohérents. Pour une théorie détaillée de la méthode, veuillez vous référer à des articles connexes tels que Athey et al. Les méthodes de complétion matricielle, de contrôle synthétique et de prédiction de régression sous intervention aléatoire peuvent également être unifiées dans le cadre de problèmes d'optimisation, et nous pouvons également combiner plusieurs méthodes de manière globale pour obtenir des résultats d'estimation plus robustes (Athey et.al 2019) .

Schéma de principe de complétion matricielle : L'image provient du cours de Guidon Imbens à l'AEA, où W représente l'état du traitement https://www.aeaweb.org/conference/cont-ed/2018- webcasts
Dans cette section, nous avons présenté les principales méthodes et progrès de l'inférence causale sur données de panel. Ce domaine est un domaine avec des méthodes très diverses et des progrès très rapides, mais il nécessite que les utilisateurs réfléchissent pleinement aux raisons qui les sous-tendent. Les hypothèses et les limites peuvent être utilisées pour évaluer plus précisément diverses politiques dans la pratique. En raison du manque de place, nous ne donnons ici qu’une très brève introduction.
5. Un examen des méthodes pour les effets causals hétérogènes
La combinaison de méthodes d'apprentissage automatique pour étudier les effets causals hétérogènes est en fait une tendance dans le développement de l'inférence causale ces dernières années. Introduisons d'abord l'effet causal hétérogène : l'effet de traitement hétérogène (HTE) fait référence au phénomène selon lequel les expériences produisent des effets différents sur les individus en raison de différentes caractéristiques individuelles des échantillons. Exprimé en combinaison avec des formules mathématiques, le HTE revêt de nombreuses formes :
L'effet causal ITE (effet de traitement individuel) de chaque individu : τi=Yi1-Yi0, un seul de Yi1 et Yi0 peut être observé, l'autre et τ i doit être estimé par une certaine méthode de modèle.
L'effet causal moyen du groupe sur certaines caractéristiques. Nous utilisons ici l'Effet : τ(x)=E[Y1-Y0|X=x].
La méthode d’analyse de HTE propose actuellement un large éventail de scénarios d’application. Grâce à HTE, nous pouvons connaître les caractéristiques des groupes qui répondent le plus à une certaine intervention stratégique. Cela peut également nous aider à étudier le mécanisme d'une stratégie de test A/B qui a l'effet attendu ou n'a aucun effet. appliqué à diverses personnalisations parmi les stratégies. Les méthodes d'inférence causale hétérogène ont de nombreuses applications dans l'industrie et sur Internet. Par exemple, TripAdvisor est utilisé pour mesurer les incitations à l'inscription des membres et Microsoft utilise cette méthode et des données à court terme pour mesurer le retour sur investissement à long terme de différents projets. trouvé Reportez-vous au cours de formation KDD 2021 (https://causal-machine-learning.github.io/kdd2021-tutorial/).
La méthode la plus courante pour les effets causals hétérogènes est en fait l'analyse multidimensionnelle couramment utilisée en analyse expérimentale. Cependant, l'utilisation de l'analyse multidimensionnelle doit se méfier du problème des tests multiples. Dans le même temps, lorsqu'il y a suffisamment de dimensions, les exigences en matière de taille de l'échantillon expérimental sont relativement élevées et l'efficacité de l'analyse est relativement faible. La méthode d'apprentissage automatique fournit des méthodes d'exploration qui améliorent l'efficacité. Son avantage est qu'elle peut apprendre de manière adaptative la distribution des effets causals hétérogènes et ne nécessite pas d'hypothèses de forme fonctionnelle strictes. Elle est meilleure que les méthodes économétriques traditionnelles basées sur la régression linéaire ou l'analyse multidimensionnelle. les méthodes ont des degrés de liberté plus élevés, mais le défi technique consiste à savoir comment faire des inférences statistiques. Ces dernières années, avec l'approfondissement de la combinaison de l'apprentissage automatique et de l'économétrie, de nombreux ensembles de méthodes ont été innovés et appliqués dans ce domaine. Nous nous concentrons ici sur les types de méthodes suivants. Les hypothèses de base de ces méthodes sont des hypothèses d'indépendance conditionnelle (. Hypothèse d’indépendance conditionnelle), c’est-à-dire que ce n’est que lorsque diverses variables confondantes sont suffisamment contrôlées que nous pouvons obtenir des estimations relativement précises des effets causals.
Forêt causale : Basée sur une forêt aléatoire, il s'agit d'une méthode non paramétrique qui effectue directement une estimation d'ajustement. La principale logique d’estimation d’un arbre causal est de définir la fonction de perte de l’arbre global en définissant l’effet causal sur chaque feuille. L'arbre causal vise à maximiser la somme des pertes de toutes les feuilles selon une certaine manière de diviser X. Outre les différents objectifs d'estimation des algorithmes d'arbres dans l'apprentissage automatique, une autre différence est que dans les algorithmes d'inférence causale, les échantillons d'ensembles d'apprentissage sont généralement divisés en ensembles d'apprentissage et en ensembles d'estimation. L'ensemble d'apprentissage est utilisé pour le partitionnement des feuilles et l'ensemble d'estimation est utilisé. utilisé Calculer l’effet moyen du traitement sur chaque nœud foliaire après le feuillage. L'avantage de l'arbre causal est que les résultats sont très concis et faciles à comprendre. Vous pouvez identifier directement les groupes de personnes présentant des différences claires dans les effets expérimentaux grâce au regroupement. Le premier indicateur regroupé est souvent la plus grande dimension de la différence dans les effets causals. . Cependant, les arbres causals sont sujets au surajustement. Dans les travaux pratiques, il est recommandé d'utiliser des forêts aléatoires causales (pour plus de détails, veuillez vous référer à Athey et Imbens 2016, Wager et Athey 2018. Dans le même temps, les forêts causales aléatoires ont également de meilleurs résultats). propriétés d'inférence statistique. Pour l'expansion de cette méthode, veuillez vous référer aux travaux de recherche tels que Athey, Tibshirani et Wager (2019) et Friedberg et al (2020). Ces nouvelles méthodes peuvent traiter davantage les problèmes lorsqu'il existe des variables confondantes et estimer les résultats de manière plus fluide. .
Meta Learners : est différent des modèles qui utilisent des arbres causals pour estimer directement les effets causals. Il s'agit d'un type de modèle d'estimation indirecte : il modélise directement la variable de résultat Y. Par conséquent, Meta Learner ne peut pas utiliser directement l'HTE estimé pour l'inférence statistique. Dans des applications pratiques, certains chercheurs utiliseront des méthodes bootstrap pour résoudre ce problème. Il existe trois types d'algorithmes d'estimation des Meta Learners : T-Learner, S-Learner et X-Learner. La différence fondamentale entre les trois méthodes est la suivante :
La plus simple est S-learner. Il utilise la variable intermédiaire comme variable caractéristique pour la modélisation ponctuelle, ce qui convient aux situations où les variables de traitement et de résultat sont fortement corrélées, sinon le modèle ne peut pas identifier le changement du résultat causé par les changements de la variable intermédiaire
;Le plus compliqué est T-learner. Il identifie les effets causals en forçant deux modèles à apprendre respectivement Yi1 du groupe expérimental et Yi0 du groupe témoin. Il peut être utilisé lorsque les valeurs d'observation variables du groupe expérimental et du groupe témoin sont plus élevées. et plus moyen, sinon l'un d'eux Le modèle sera plus régularisé
X-learner est une méthode relativement nouvelle en utilisant une estimation en deux étapes et une correction du score de propension, il peut faire des comparaisons avec une petite quantité de. données Bonne estimation (voir Künzel et al. 2019 pour plus de détails).
Cadre d'estimation basé sur DML et DRL : Nous introduisons ces deux cadres en combinaison avec l'outil Econml de Microsoft :
https://www.microsoft.com/en-us /research /project/econml/
DML (double machine learning) est un cadre qui confond de manière flexible les variables et traite la relation entre les variables et les variables de résultat lorsque des variables confondantes de grande dimension existent. principalement divisé en deux étapes lors de l'estimation de l'effet causal : la première étape consiste à utiliser deux modèles d'apprentissage automatique (pas nécessairement les mêmes) pour estimer E(Y|X,W) et E(T| X, W) deux attentes conditionnelles, puis prenez le résidu. Ici, X et W sont des variables confusionnelles, mais seul X est la variable pertinente dans CATE. La deuxième étape consiste à estimer ATE ou CATE sur la base du résidu. Lors de l'estimation de CATE, le résidu de T-E(T|X,W) est multiplié par une fonction θ(X) autour de X pour l'estimation. Pour plus d’informations sur la façon d’estimer l’ATE, veuillez consulter Chernozhukov et al. Econml propose de nombreux modèles parmi lesquels choisir dans la deuxième étape : LinearDML (en utilisant le modèle OLS), DML (en utilisant un modèle personnalisé), CausalForestDML (en utilisant une forêt aléatoire causale)... Lorsque vous utilisez le framework DML, vous devez veiller à vérifier si les moyennes des termes résiduels des deux modèles sont significativement différentes de 0 ou significativement corrélées. Si tel est le cas, cela signifie que les variables confondantes ne sont peut-être pas suffisamment contrôlées.
Le framework DRL est basé sur la méthode Doublement Robuste, qui est également divisée en deux étapes. La première étape utilise X, W, T pour prédire Y et définit la valeur prédite comme gt. (X, W); La deuxième étape utilise un modèle de classification pour prédire T en utilisant Il convient de noter que T ici est une variable discrète et restreint gt(X,W) à une sorte de modèle basé sur la régression. Après le résultat en deux étapes, une variable de résultat ajustée est calculée :
Ensuite, le Y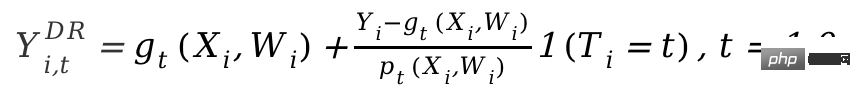
i,tDR ajusté est dans le groupe expérimental et le contrôle Regroupez la différence Yi1DR-Yi0DR, et renvoyez X pour obtenir CATE. La raison pour laquelle DRL est appelé Doublement Robuste est que dans la formule ci-dessus, tant que l'un des gt(X,W) et pt(X,W) est correct, l'effet causal sera estimé. Il est impartial. Mais si les deux estimations du modèle sont fausses, l’erreur qui en résulte peut être très importante. Semblable au DML, la différence entre les différents apprenants de DRL dans Econml réside dans le type de modèle utilisé pour adapter Y avec .
Le plus grand défi d'application des méthodes d'inférence causale hétérogène basées sur des modèles d'apprentissage automatique est en fait de savoir comment sélectionner un modèle d'apprentissage automatique approprié et ajuster les paramètres pour obtenir des résultats d'estimation relativement robustes. Sur la base de l'expérience d'application et des recherches récentes, les précautions suivantes doivent être prises :
- Assurez-vous que la taille de l'échantillon de formation est suffisamment grande.
-
Si vous utilisez l'outil Econml, il est recommandé d'utiliser la fonction score* pour sélectionner le modèle (plus le score est petit, meilleur est le modèle), mais tous les modèles n'ont pas cette fonction : par exemple, DML l'a mais pas X-Learner ou Causal Forest. Si vous utilisez Causalml d'Uber, vous pouvez utiliser le graphique de gain cumulatif pour comparer les performances de différents méta-apprenants.
https://github.com/uber/causalml. - Certaines méthodes peuvent effectuer des tests statistiques sur HTE, mais d'autres ne le peuvent pas. Dans Econml, les méthodes qui peuvent être utilisées pour effectuer des tests statistiques sur HTE sont limitées à la méthode dans laquelle la dernière étape du modèle dans DML/DRL est définie sur un modèle linéaire ou une forêt causale, tandis que la variable de caractéristique X et la Les variables expérimentales T sont liées de manière non linéaire dans de nombreux scénarios commerciaux. Le choix forcé d'un modèle linéaire peut entraîner un biais d'estimation de HTE (par exemple, la volatilité de HTE n'a rien à voir avec X et n'est que du bruit). Si des individus présentant une HTE significative doivent être dépistés pour une analyse ultérieure, une correction de tests multiples pour les tests d'effets individuels est nécessaire.
- En plus du degré d'ajustement du modèle, une norme est également nécessaire pour mesurer la qualité de l'estimation HTE : par exemple, si la variation de HTE est suffisamment importante pour distinguer les groupes sensibles des groupes non sensibles, vous peut se référer à la méthode proposée par Chernozhukov et al. (2018). L'inférence statistique basée sur les caractéristiques HTE est également très facile à appliquer.
Les méthodes présentées ci-dessus se concentrent essentiellement sur l'effet causal hétérogène statique sous une variable intermédiaire. Mais dans les applications pratiques, les problèmes que nous rencontrerons seront plus complexes. Par exemple, de multiples variables intervenantes sont impliquées : les incitations en matière de subventions fournies par le produit aux utilisateurs peuvent inclure à la fois des incitations à la connexion et des récompenses pour d'autres tâches. La manière d'équilibrer la répartition des différents types d'incitations peut être définie comme une construction à effet causal hétérogène. de multiples variables intervenantes dans des problèmes de modélisation et d'optimisation. Un autre exemple est celui des effets causals dynamiques, dans lesquels les variables confusionnelles changent avec l'intervention à différents moments (voir Lewis et Syrgkanis 2020). Prenons l'exemple des tâches d'incitation. Ces tâches peuvent amener les utilisateurs à prêter attention à de nouvelles ancres, modifiant ainsi leurs préférences en matière de visualisation du contenu, et affecteront également l'effet des incitations ultérieures. Ces scénarios complexes ont inspiré l’expansion de diverses méthodes, et nous attendons également avec impatience l’émergence de recherches et d’applications plus établies et plus systématiques à l’avenir.
Modèle causal structurel
Dans la section précédente, nous avons présenté les idées principales et le développement méthodologique des modèles de résultats latents. Ce type de méthode scolaire a une théorie statistique relativement complète et peut obtenir des résultats d'estimation relativement précis. Cependant, il existe certaines limites. Il ne peut être utilisé que pour estimer l'influence d'un seul degré de corrélation entre les variables (c'est-à-dire qu'une seule variable dépendante et certaines variables indépendantes sont autorisées, et les liens d'effets indirects ne peuvent pas être estimés). la relation entre de nombreuses variables Les liens et les relations complexes nécessitent l'utilisation d'une autre école de méthodes de modèles causals structurels.
Le modèle causal structurel utilise un graphe acyclique dirigé (DAG) pour décrire la relation causale et la distribution conditionnelle entre les variables. Chaque nœud du graphe est une variable, et la relation causale est représentée par les arêtes reliant ces nœuds. Par exemple, X11, on appelle aussi X. 1 un nœud enfant, et Pour un DAG formé d'un ensemble de variables aléatoires X=(X1, P(X)=∏pj=1P( est X Le nœud parent immédiat de j. Lorsque nous exprimons la relation causale, nous introduisons le concept d'opérateur do, en supposant que le courant X=(X1, )=(x1,x2 ,...xp), utilisez do(Xj=x ' j) représente l'intervention pour la variable P(X1 =x1, p =xp|do(Xj=x 'j)) , le changement attendu de chaque variable selon l'ancienne et la nouvelle distribution est l'effet causal de sur elles, tel que E(X1|do)( 1|do(X j=xj)). Judea Pearl, la fondatrice du modèle causal des résultats, a souligné dans ses recherches que lors de l'utilisation de diagrammes de causalité pour identifier les relations causales, si le « critère de la porte dérobée » et le « critère de la porte d'entrée » sont remplis, il n'est pas réellement nécessaire d'observer toutes les variables. Concernant les détails spécifiques, veuillez vous référer à Pearl (2009) pour les détails théoriques. Il convient d’ajouter que le modèle causal structurel et le modèle de résultats potentiels sont en réalité liés. Dans les applications pratiques, nous ne disposons peut-être pas directement des informations nécessaires pour définir un graphe causal, donc comment apprendre la structure du graphe causal entre les variables est devenu une question importante. Lors de la résolution de ce type de problème, nous devons d'abord clarifier les hypothèses requises : Hypothèse causale de Markov : Cette hypothèse signifie que la distribution conditionnelle de tout nœud est basée uniquement sur son nœud parent direct. Hypothèse de suffisance causale : Cette hypothèse équivaut à l'absence de variables confondantes non observées. Hypothèse de fidélité causale : Cette hypothèse signifie que, sur la base d'une distribution de probabilité conditionnelle, certains nœuds sont indépendants les uns des autres (le graphique peut donc être coupé). Les algorithmes sont grossièrement divisés en deux catégories : Pour une introduction détaillée, veuillez vous référer à Glymour, Zhang et Sprites (2019) et à l'article "Statistical Methods of Causal Inference" dans "Science China : Mathématiques" Numéro 12, 2018 》: https://cosx.org/2022/10/causality-statistical-method/. Algorithmes basés sur les contraintes : Apprenez tous les graphiques causals qui satisfont aux hypothèses de fidélité et de markov causal basées sur le test d'indépendance de la distribution conditionnelle, c'est-à-dire testez si la distribution conditionnelle entre deux nœuds est indépendante. Par exemple, l'algorithme PC (Spirtes et Glymour 1991) et l'algorithme IC (Verma et Pearl 1990). Algorithmes basés sur les scores : Trouvez la structure graphique qui correspond le mieux aux données en optimisant un certain score défini. Les équations structurelles et les fonctions de score doivent être définies. Par exemple, l'algorithme CGNN (Goudet et al. 2017) et l'algorithme NOTEARS (Zheng et al. 2018). Ici, nous nous concentrons sur l'algorithme NOTEARS. L'algorithme traditionnel est basé sur tous les nœuds et les relations possibles entre les nœuds, recherchant dans tous les graphiques possibles et sélectionnant la solution optimale selon une certaine norme. Il s'agit d'un problème NP-difficile typique qui prend beaucoup de temps. Les ressources informatiques de longue date et actuelles sont fondamentalement incapables de répondre aux besoins informatiques. L'algorithme NOTEARS transforme le problème de recherche discrète en un problème de recherche continue. Cet algorithme améliore considérablement la vitesse de calcul et le rend utilisable par les analystes de données ordinaires. Cependant, cette méthode présente également certaines limites. Par exemple, on suppose que le bruit de toutes les variables doit être distribué de manière gaussienne. Ces dernières années, de plus en plus de méthodes (telles que He et al. 2021) ont tenté d'améliorer les hypothèses de. de telles méthodes. Avec le développement du domaine de l'apprentissage par renforcement, nous avons également découvert que l'inférence causale et l'apprentissage par renforcement peuvent être combinés pour favoriser le développement de chacun. L'inférence causale peut aider les algorithmes d'apprentissage par renforcement à apprendre plus efficacement les fonctions de valeur ou les stratégies optimales en déduisant la relation causale entre les états ou entre les états et les actions dans l'apprentissage par renforcement. Les lecteurs intéressés par cet aspect peuvent se référer au professeur Elias Bareinboim des cours de l'Université de Columbia (. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). D'autre part, l'apprentissage par renforcement peut également être intégré à l'algorithme d'apprentissage des graphiques causals, comme Zhu, Ng et Chen (2019) du laboratoire Noah's Ark de Huawei. Concernant les perspectives d'avenir de l'inférence causale, il convient de mentionner un nouveau paradigme de recherche lié à l'apprentissage des graphes, à l'inférence causale et à l'apprentissage automatique ces dernières années : il s'agit du concept « d'apprentissage stable » proposé par l'équipe du professeur Cui Peng. de l’Université Tsinghua (Cui et Athey 2022). L'application de modèles tels que l'apprentissage automatique et l'intelligence artificielle repose sur une hypothèse importante : l'hypothèse d'indépendance et de distribution identique. C'est-à-dire que l'ensemble de formation et l'ensemble de test doivent provenir de la même distribution, mais en fait, il existe divers problèmes OOD (Out Of Distribution, out of distribution). À l'heure actuelle, les performances du modèle ne peuvent pas être garanties. C'est aussi un problème auquel sont confrontés divers modèles dans l'histoire, un risque technique important. L’inférence causale peut aider à surmonter de tels problèmes. S'il peut être garanti qu'une structure a le même effet prédictif dans divers environnements pour résoudre le problème OOD, alors cette structure doit être une structure causale et les performances d'une structure causale dans divers environnements sont relativement stables. Les recherches menées par l'équipe de Cui Peng (He et al. 2022, Shen et al. 2021) ont révélé qu'en utilisant l'idée de confondre l'équilibre d'appariement des variables, toutes les variables peuvent être rendues indépendantes en repondérant l'échantillon, faisant ainsi d'un modèle basé sur la corrélation un modèle basé sur les causes et les effets. L'apprentissage dit stable consiste à utiliser un ensemble d'apprentissage d'une distribution et un ensemble de test de plusieurs distributions inconnues différentes. L'objectif d'optimisation est de minimiser la variance de précision. Je pense qu'il s'agit d'un domaine très important à l'avenir et que les lecteurs intéressés peuvent continuer à prêter attention aux progrès de la recherche pertinents. Comparaison de l'apprentissage indépendant et distribué à l'identique, de l'apprentissage par transfert et de l'apprentissage stable : images de l'article Cui et Athey 2022 Dans les applications pratiques, les systèmes de recommandation, la vision par ordinateur, la conduite automatique , naturel L'inférence causale et l'apprentissage de graphes causals ne manquent pas dans les domaines liés à l'apprentissage automatique et à l'intelligence artificielle tels que le traitement du langage, ce qui a favorisé le développement de ces domaines. Nous énumérons également ici quelques exemples d'applications plus détaillées liées à ces dernières années. à l'apprentissage automatique. Pour les simulateurs de référence et les ensembles de données, veuillez vous référer au résumé des chercheurs de l'UCL et de l'Université d'Oxford (Kaddour et al. 2022). Dans le domaine des systèmes de recommandation, comme nous l'avons introduit dans l'application des méthodes de variables instrumentales, les systèmes de recommandation comportent inévitablement des biais. L'identification de la relation graphique causale entre les utilisateurs et les éléments peut aider le système de recommandation à corriger les biais. Par exemple, Wang et al. (2021) et Zhang et al. (2021) ont utilisé des diagrammes de causalité pour éliminer respectivement les biais causés par le clickbait et la popularité. Dans le domaine de la conduite autonome, des chercheurs de Microsoft ont lancé CausalCity (McDuff et al. 2022), une plateforme d'environnement de conduite simulée qui intègre l'inférence causale dans la prédiction de trajectoire des véhicules. Dans le domaine du traitement du langage naturel, les chercheurs ont découvert que l'inférence causale peut aider les méthodes de PNL à être plus robustes et compréhensibles (Zeng et al. 2020), notamment en testant les biais dans les modèles de langage et les corpus (Vig et al. 2020)... I Je crois qu'à l'avenir, l'inférence causale continuera à prospérer, jouant un rôle important dans ces domaines et dans d'autres. 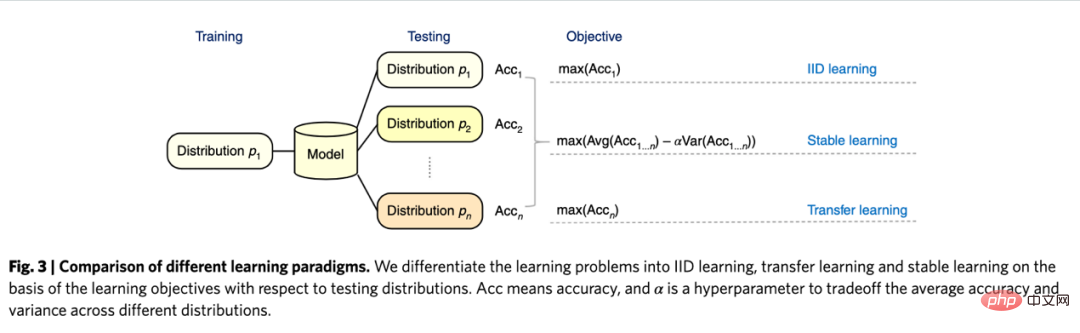
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
Écrit ci-dessus et compréhension personnelle de l'auteur : À l'heure actuelle, dans l'ensemble du système de conduite autonome, le module de perception joue un rôle essentiel. Le véhicule autonome roulant sur la route ne peut obtenir des résultats de perception précis que via le module de perception en aval. dans le système de conduite autonome, prend des jugements et des décisions comportementales opportuns et corrects. Actuellement, les voitures dotées de fonctions de conduite autonome sont généralement équipées d'une variété de capteurs d'informations de données, notamment des capteurs de caméra à vision panoramique, des capteurs lidar et des capteurs radar à ondes millimétriques pour collecter des informations selon différentes modalités afin d'accomplir des tâches de perception précises. L'algorithme de perception BEV basé sur la vision pure est privilégié par l'industrie en raison de son faible coût matériel et de sa facilité de déploiement, et ses résultats peuvent être facilement appliqués à diverses tâches en aval.
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
La couche inférieure de la fonction de tri C++ utilise le tri par fusion, sa complexité est O(nlogn) et propose différents choix d'algorithmes de tri, notamment le tri rapide, le tri par tas et le tri stable.
 L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
La convergence de l’intelligence artificielle (IA) et des forces de l’ordre ouvre de nouvelles possibilités en matière de prévention et de détection de la criminalité. Les capacités prédictives de l’intelligence artificielle sont largement utilisées dans des systèmes tels que CrimeGPT (Crime Prediction Technology) pour prédire les activités criminelles. Cet article explore le potentiel de l’intelligence artificielle dans la prédiction de la criminalité, ses applications actuelles, les défis auxquels elle est confrontée et les éventuelles implications éthiques de cette technologie. Intelligence artificielle et prédiction de la criminalité : les bases CrimeGPT utilise des algorithmes d'apprentissage automatique pour analyser de grands ensembles de données, identifiant des modèles qui peuvent prédire où et quand les crimes sont susceptibles de se produire. Ces ensembles de données comprennent des statistiques historiques sur la criminalité, des informations démographiques, des indicateurs économiques, des tendances météorologiques, etc. En identifiant les tendances qui pourraient échapper aux analystes humains, l'intelligence artificielle peut donner du pouvoir aux forces de l'ordre.
 Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
01Aperçu des perspectives Actuellement, il est difficile d'atteindre un équilibre approprié entre efficacité de détection et résultats de détection. Nous avons développé un algorithme YOLOv5 amélioré pour la détection de cibles dans des images de télédétection optique haute résolution, en utilisant des pyramides de caractéristiques multicouches, des stratégies de têtes de détection multiples et des modules d'attention hybrides pour améliorer l'effet du réseau de détection de cibles dans les images de télédétection optique. Selon l'ensemble de données SIMD, le mAP du nouvel algorithme est 2,2 % meilleur que YOLOv5 et 8,48 % meilleur que YOLOX, permettant ainsi d'obtenir un meilleur équilibre entre les résultats de détection et la vitesse. 02 Contexte et motivation Avec le développement rapide de la technologie de télédétection, les images de télédétection optique à haute résolution ont été utilisées pour décrire de nombreux objets à la surface de la Terre, notamment des avions, des voitures, des bâtiments, etc. Détection d'objets dans l'interprétation d'images de télédétection
 Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
1. Le développement historique des grands modèles multimodaux. La photo ci-dessus est le premier atelier sur l'intelligence artificielle organisé au Dartmouth College aux États-Unis en 1956. Cette conférence est également considérée comme le coup d'envoi du développement de l'intelligence artificielle. pionniers de la logique symbolique (à l'exception du neurobiologiste Peter Milner au milieu du premier rang). Cependant, cette théorie de la logique symbolique n’a pas pu être réalisée avant longtemps et a même marqué le début du premier hiver de l’IA dans les années 1980 et 1990. Il a fallu attendre la récente mise en œuvre de grands modèles de langage pour découvrir que les réseaux de neurones portent réellement cette pensée logique. Les travaux du neurobiologiste Peter Milner ont inspiré le développement ultérieur des réseaux de neurones artificiels, et c'est pour cette raison qu'il a été invité à y participer. dans ce projet.
 Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
1. Contexte de la construction de la plateforme 58 Portraits Tout d'abord, je voudrais partager avec vous le contexte de la construction de la plateforme 58 Portraits. 1. La pensée traditionnelle de la plate-forme de profilage traditionnelle ne suffit plus. La création d'une plate-forme de profilage des utilisateurs s'appuie sur des capacités de modélisation d'entrepôt de données pour intégrer les données de plusieurs secteurs d'activité afin de créer des portraits d'utilisateurs précis. Elle nécessite également l'exploration de données pour comprendre le comportement et les intérêts des utilisateurs. et besoins, et fournir des capacités côté algorithmes ; enfin, il doit également disposer de capacités de plate-forme de données pour stocker, interroger et partager efficacement les données de profil utilisateur et fournir des services de profil. La principale différence entre une plate-forme de profilage d'entreprise auto-construite et une plate-forme de profilage de middle-office est que la plate-forme de profilage auto-construite dessert un seul secteur d'activité et peut être personnalisée à la demande. La plate-forme de mid-office dessert plusieurs secteurs d'activité et est complexe ; modélisation et offre des fonctionnalités plus générales. 2.58 Portraits d'utilisateurs de l'arrière-plan de la construction du portrait sur la plate-forme médiane 58
 Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Écrit ci-dessus & La compréhension personnelle de l'auteur est que dans le système de conduite autonome, la tâche de perception est un élément crucial de l'ensemble du système de conduite autonome. L'objectif principal de la tâche de perception est de permettre aux véhicules autonomes de comprendre et de percevoir les éléments environnementaux environnants, tels que les véhicules circulant sur la route, les piétons au bord de la route, les obstacles rencontrés lors de la conduite, les panneaux de signalisation sur la route, etc., aidant ainsi en aval modules Prendre des décisions et des actions correctes et raisonnables. Un véhicule doté de capacités de conduite autonome est généralement équipé de différents types de capteurs de collecte d'informations, tels que des capteurs de caméra à vision panoramique, des capteurs lidar, des capteurs radar à ondes millimétriques, etc., pour garantir que le véhicule autonome peut percevoir et comprendre avec précision l'environnement environnant. éléments , permettant aux véhicules autonomes de prendre les bonnes décisions pendant la conduite autonome. Tête





