Incroyable! Utilisez Numpy pour développer un cadre d'apprentissage en profondeur et examiner le processus de formation des réseaux neuronaux

Bonjour à tous.

Aujourd'hui, j'aimerais partager avec vous un projet open source très génial. J'ai développé un framework d'apprentissage profond en utilisant Numpy. La syntaxe est fondamentalement la même que celle de Pytorch.

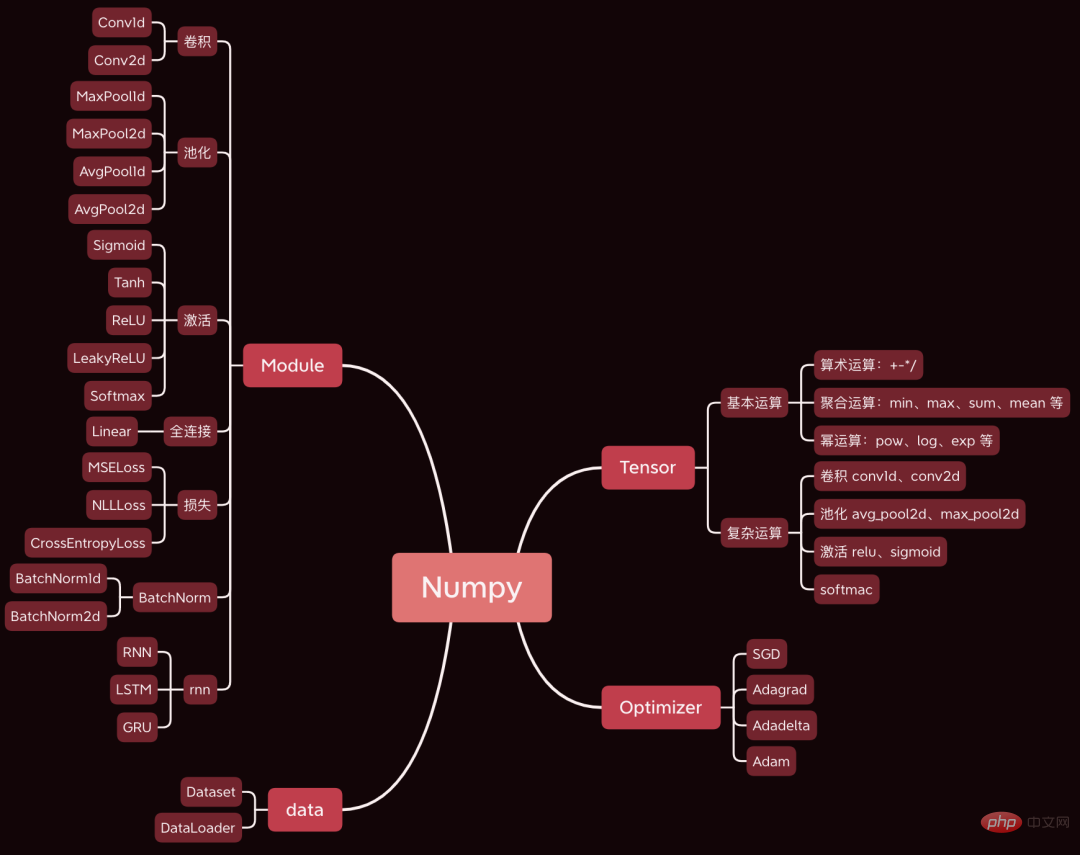
Aujourd'hui, nous prenons comme exemple un simple réseau neuronal convolutif pour analyser le code source des étapes principales impliquées dans le processus de formation du réseau neuronal, telles que la propagation avant, la propagation arrière et l'optimisation des paramètres.

Les ensembles de données et les codes utilisés ont été regroupés, et il existe des moyens de les obtenir à la fin de l'article.

1. Préparation

Préparez d'abord les données et le code.

1.1 Construisez le réseau

Tout d'abord, téléchargez le code source du framework, adresse : https://github.com/duma-repo/PyDyNet

git clone https://github.com/duma-repo/PyDyNet.git

Construisez le réseau neuronal convolutif LeNet et entraînez le modèle à trois classifications.

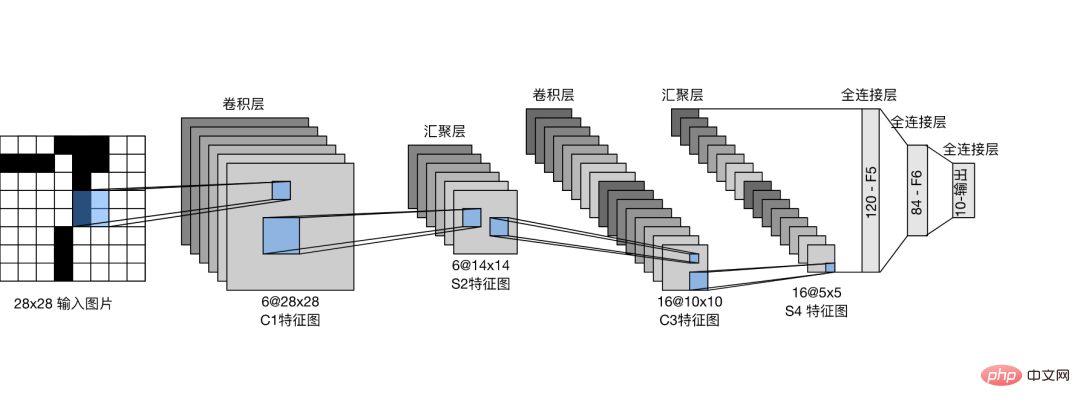
Créez le fichier de code directement dans le répertoire PyDyNet.

from pydynet import nn

class LeNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avg_pool = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
self.sigmoid = nn.Sigmoid()
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 3)

def forward(self, x):
x = self.conv1(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = self.conv2(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = x.reshape(x.shape[0], -1)

x = self.fc1(x)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)

return x

Vous pouvez voir que la définition du réseau est exactement la même que la syntaxe Pytorch.

Dans le code source que j'ai fourni, la fonction récapitulative est prévue pour imprimer la structure du réseau.

1.2 Préparer les données

Les données d'entraînement utilisent l'ensemble de données Fanshion-MNIST, qui contient 10 catégories d'images, 6 000 images dans chaque catégorie.

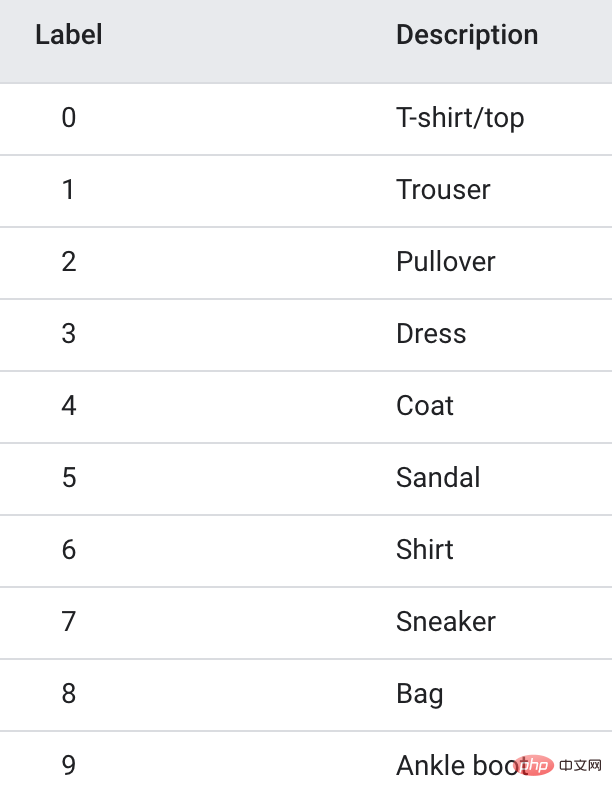
Afin d'accélérer l'entraînement, j'ai extrait uniquement les 3 premières catégories, soit un total de 1,80 000 images d'entraînement, pour réaliser un modèle à trois classifications.

1.3 Formation du modèle

import pydynet
from pydynet import nn
from pydynet import optim

lr, num_epochs = 0.9, 10
optimizer = optim.SGD(net.parameters(),
lr=lr)
loss = nn.CrossEntropyLoss()

for epoch in range(num_epochs):
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()

with pydynet.no_grad():
metric.add(l.numpy() * X.shape[0],
 accuracy(y_hat, y),
 X.shape[0])

Le code de formation est également le même que celui de Pytorch.

La chose clé à faire ensuite est de se plonger dans le code source de la formation sur modèle pour apprendre les principes de la formation sur modèle.

2. train, no_grad et eval

net.train seront appelés avant que le modèle ne commence l'entraînement.

def train(self, mode: bool = True):
set_grad_enabled(mode)
self.set_module_state(mode)

Vous pouvez voir qu'il définira grad​(gradient) sur True​, et le Tensor créé par la suite peut avoir un dégradé. Une fois que Tensor a apporté le gradient, il sera placé dans le graphique de calcul et attendra la dérivation pour calculer le gradient.

Ce qui suit avec no_grad() : le code

class no_grad:
def __enter__(self) -> None:
self.prev = is_grad_enable()
set_grad_enabled(False)

définira grad​(gradient) sur False​, afin que le Tensor créé ultérieurement ne soit pas placé dans le graphe de calcul, et naturellement il n'est pas nécessaire de calculer le gradient, ce qui peut accélérer l’inférence.

Nous voyons souvent l'utilisation de net.eval() dans Pytorch, et nous examinons également son code source.

def eval(self):
return self.train(False)

Vous pouvez voir qu'il appelle directement train(False)​ pour désactiver le dégradé, et l'effet est similaire à no_grad().

Donc, appelez généralement le train pour activer la pente avant l'entraînement. Après la formation, appelez eval pour fermer le gradient afin de faciliter une inférence rapide.

3. Propagation vers l'avant

En plus de calculer la probabilité de catégorie, la chose la plus importante dans la propagation vers l'avant est d'organiser les tenseurs du réseau dans un graphe de calcul dans l'ordre de propagation vers l'avant. rétro-propagation. Le gradient du tenseur.

Le Tensor dans les réseaux de neurones n'est pas seulement utilisé pour stocker des données, mais aussi pour calculer et stocker des gradients.

Prenons l'exemple de l'opération de convolution de la première couche pour voir comment générer un graphique de calcul.

def conv2d(x: tensor.Tensor,
 kernel: tensor.Tensor,
 padding: int = 0,
 stride: int = 1):
'''二维卷积函数
'''
N, _, _, _ = x.shape
out_channels, _, kernel_size, _ = kernel.shape
pad_x = __pad2d(x, padding)
col = __im2col2d(pad_x, kernel_size, stride)
out_h, out_w = col.shape[-2:]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
col_filter = kernel.reshape(out_channels, -1).T
out = col @ col_filter
return out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

x​ est l'image d'entrée et n'a pas besoin d'enregistrer le dégradé. Le noyau est le poids du noyau de convolution et doit calculer le gradient.

Ainsi, le nouveau tenseur généré par pad_x = __pad2d(x, padding)​ n'a pas non plus de dégradé, il n'a donc pas besoin d'être ajouté au graphe de calcul.

Le tenseur généré par kernel.reshape(out_channels, -1)​ doit calculer le gradient et doit également être ajouté au graphique de calcul.

Jetons un coup d'œil au processus de jointure :

def reshape(self, *new_shape):
return reshape(self, new_shape)

class reshape(UnaryOperator):
'''
张量形状变换算子，在Tensor中进行重载

Parameters
----------
new_shape : tuple
变换后的形状，用法同NumPy
'''
def __init__(self, x: Tensor, new_shape: tuple) -> None:
self.new_shape = new_shape
super().__init__(x)

def forward(self, x: Tensor)
return x.data.reshape(self.new_shape)

def grad_fn(self, x: Tensor, grad: np.ndarray)
return grad.reshape(x.shape)

La fonction reshape​ renverra un objet de classe reshape​ hérite de la classe UnaryOperator​, et dans la fonction __init__, la fonction d'initialisation de la classe parent est appelée. La classe

class UnaryOperator(Tensor):
def __init__(self, x: Tensor) -> None:
if not isinstance(x, Tensor):
x = Tensor(x)
self.device = x.device
super().__init__(
data=self.forward(x),
device=x.device,
# 这里 requires_grad 为 True
requires_grad=is_grad_enable() and x.requires_grad,
)

UnaryOperator​ hérite de la classe Tensor​, donc l'objet reshape​ est également un tenseur.

Dans la fonction __init__​ d'UnaryOperator, appelez la fonction d'initialisation de Tensor et le paramètre requis_grad transmis est True, ce qui signifie que le gradient doit être calculé. Le code de calcul de

requires_grad​ est is_grad_enable() et x.requires_grad. is_grad_enable()​ a été défini sur True par train, et x​ est le noyau de convolution, et son require_grad​ est également True.

class Tensor:
def __init__(
self,
data: Any,
dtype=None,
device: Union[Device, int, str, None] = None,
requires_grad: bool = False,
) -> None:
if self.requires_grad:
# 不需要求梯度的节点不出现在动态计算图中
Graph.add_node(self)

Enfin, dans la méthode d'initialisation de la classe Tensor, appelez Graph.add_node(self) pour ajouter le tenseur actuel au graphe de calcul.

De même, les nouveaux tenseurs que l'on voit couramment ci-dessous utilisant le tenseur qui require_grad=True seront placés dans le graphique de calcul.

Après une opération de convolution, 6 nœuds seront ajoutés au graphe de calcul.

4. Rétropropagation

Une fois la propagation vers l'avant terminée, commencez par le dernier nœud du graphique de calcul et effectuez une rétropropagation d'arrière en avant.

l = loss(y_hat, y)
l.backward()

se propage couche par couche à travers le réseau aller et atteint finalement le tenseur de perte l.

En prenant l comme point de départ et en se propageant d'avant en arrière, le gradient de chaque nœud du graphe de calcul peut être calculé.

Le code de base de l'arrière est le suivant :

def backward(self, retain_graph: bool = False):

for node in Graph.node_list[y_id::-1]:
grad = node.grad
for last in [l for l in node.last if l.requires_grad]:
add_grad = node.grad_fn(last, grad)

last.grad += add_grad

Graph.node_list[y_id::-1] trie le graphique de calcul dans l'ordre inverse.

node​是前向传播时放入计算图​中的每个tensor。

node.last​ 是生成当前tensor的直接父节点。

调用node.grad_fn计算梯度，并反向传给它的父节点。

grad_fn​其实就是Tensor的求导公式，如：

class pow(BinaryOperator):
'''
幂运算算子，在Tensor类中进行重载

See also
--------
add : 加法算子
'''
def grad_fn(self, node: Tensor, grad: np.ndarray)
if node is self.last[0]:
return (self.data * self.last[1].data / node.data) * grad

return​后的代码其实就是幂函数求导公式。

假设y=x^2，x​的导数为2x。

5. 更新参数

反向传播计算梯度后，便可以调用优化器，更新模型参数。

l.backward()
optimizer.step()

本次训练我们用梯度下降SGD算法优化参数，更新过程如下：

def step(self):
for i in range(len(self.params)):
grad = self.params[i].grad + self.weight_decay * self.params[i].data
self.v[i] *= self.momentum
self.v[i] += self.lr * grad
self.params[i].data -= self.v[i]
if self.nesterov:
self.params[i].data -= self.lr * grad

self.params​是整个网络的权重，初始化SGD时传进去的。

step​函数最核心的两行代码，self.v[i] += self.lr * grad​ 和 self.params[i].data -= self.v[i]​，用当前参数 - 学习速率 * 梯度​更新当前参数。

这是机器学习的基础内容了，我们应该很熟悉了。

一次模型训练的完整过程大致就串完了，大家可以设置打印语句，或者通过DEBUG的方式跟踪每一行代码的执行过程，这样可以更了解模型的训练过程。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!