CRPS : fonction de notation pour les modèles d'apprentissage automatique bayésiens

Le score de probabilité classée continue (CRPS) ou « score de probabilité classée continue » est une fonction ou une statistique qui compare les prédictions de distribution aux valeurs réelles.

Une partie importante du flux de travail d'apprentissage automatique est l'évaluation du modèle. Le processus lui-même peut être considéré comme du bon sens : diviser les données en ensembles de formation et de test, entraîner le modèle sur l'ensemble de formation et utiliser une fonction de notation pour évaluer ses performances sur l'ensemble de test.

Une fonction de notation (ou métrique) mappe les vraies valeurs et leurs prédictions à une valeur unique et comparable [1]. Par exemple, pour des prévisions continues, vous pouvez utiliser des fonctions de notation telles que RMSE, MAE, MAPE ou R-squared. Et si la prévision n’était pas une estimation point par point, mais une distribution ?

Dans l'apprentissage automatique bayésien, les prédictions ne sont généralement pas des estimations ponctuelles, mais plutôt des distributions de valeurs. Par exemple, les prédictions peuvent être des paramètres estimés d'une distribution, ou dans le cas non paramétrique, un tableau d'échantillons provenant d'une méthode MCMC.

Dans ce cas, les fonctions de notation traditionnelles ne conviennent pas à la conception statistique ; l'agrégation des distributions prédites en leur moyenne ou médiane entraîne la perte d'informations considérables sur la dispersion et la forme de la distribution prédite.

CRPS

Continuous Graded Probability Score (CRPS) est une fonction fractionnaire qui compare une seule valeur vraie à une fonction de distribution cumulative (CDF) :

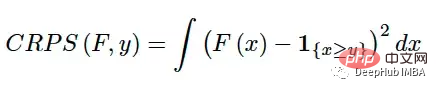
Elle a été introduite pour la première fois dans les années 1970 [4] et est principalement utilisée Les prévisions météorologiques font désormais l'objet d'une attention renouvelée dans la littérature et dans l'industrie [1][6]. Il peut être utilisé comme métrique pour évaluer les performances du modèle lorsque la variable cible est continue et que le modèle prédit la distribution de la cible. Les exemples incluent la régression bayésienne ou les modèles de séries chronologiques bayésiennes [5].

CRPS est utile pour les prédictions paramétriques et non paramétriques en utilisant CDF : pour de nombreuses distributions, CRPS [3] a une expression analytique, et pour les prédictions non paramétriques, CRPS utilise la fonction de distribution cumulative empirique (eCDF).

Après avoir calculé le CRPS pour chaque observation de l'ensemble de test, vous devez également regrouper les résultats en une seule valeur. Semblables au RMSE et au MAE, ils sont résumés à l'aide d'une moyenne (éventuellement pondérée) :

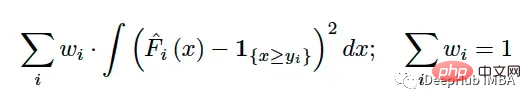
Le principal défi lors de la comparaison d'une valeur unique à une distribution est de savoir comment convertir la valeur unique en une représentation de la distribution. CRPS résout ce problème en convertissant la vérité terrain en une distribution dégénérée avec une fonction indicatrice. Par exemple, si la vraie valeur est 7, nous pouvons utiliser :

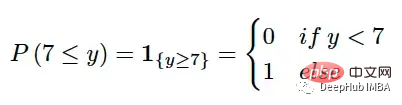
La fonction indicateur est un CDF valide et peut répondre à toutes les exigences d'un CDF. La distribution prédite peut alors être comparée à la distribution dégénérée des valeurs vraies. Nous voulons absolument que la distribution prédite soit aussi proche que possible de la réalité ; cela peut donc être exprimé mathématiquement en mesurant l'aire (au carré) entre ces deux CDF :

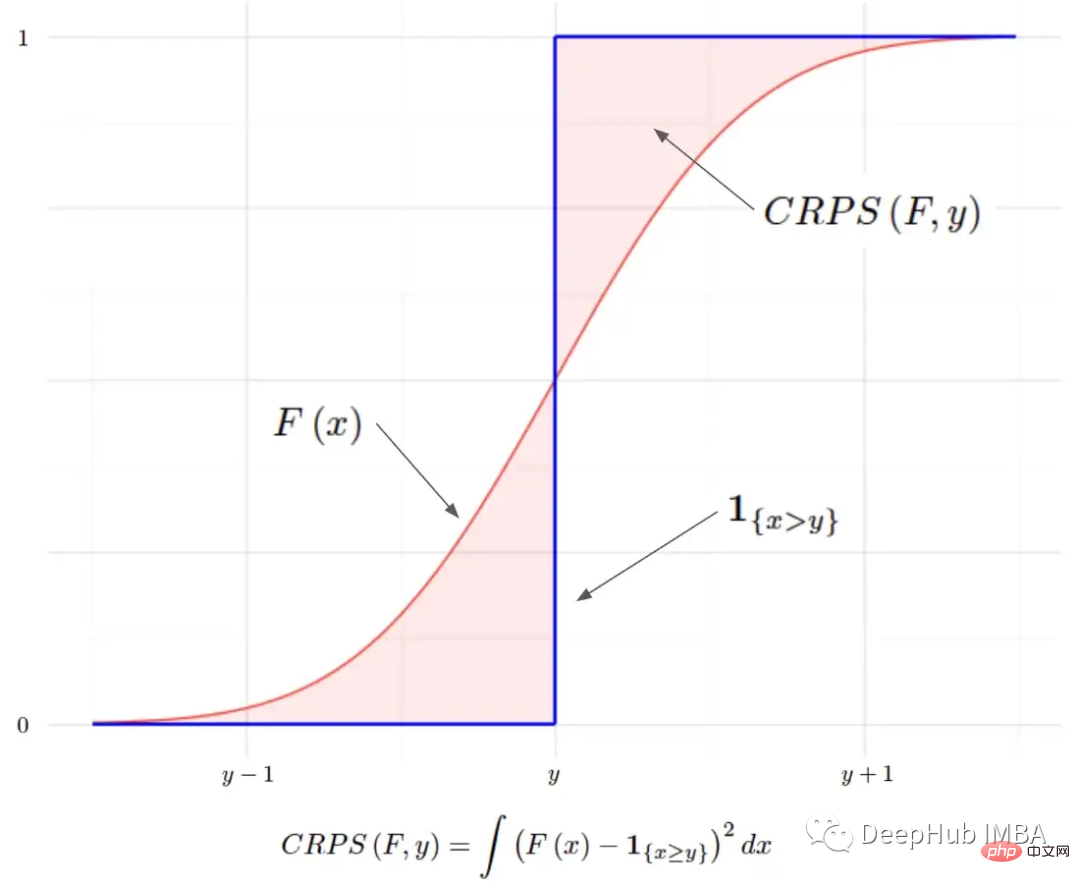
Relation MAE à MAE

CRPS au fameux MAE ( Erreur moyenne absolue) sont étroitement liés. Si nous prenons une prédiction ponctuelle et la traitons comme une CDF dégénérée et l'injectons dans l'équation CRPS, nous obtenons :

Donc, si la distribution de prédiction est une distribution dégénérée (par exemple, une estimation ponctuelle), la CRPS réduire en MAE. Cela nous aide à comprendre le CRPS sous un autre angle : cela peut être considéré comme une généralisation du MAE à la prédiction des distributions, ou que le MAE est un cas particulier du CRPS lorsque la distribution de prédiction dégénère.

Lorsque la prédiction du modèle est une distribution paramétrique (par exemple, les paramètres de distribution doivent être prédits), CRPS a une expression analytique pour certaines distributions courantes [3]. Si le modèle prédit les paramètres μ et σ de la distribution normale, le CRPS peut être calculé à l'aide de la formule suivante :

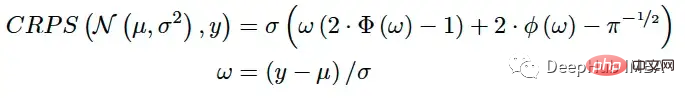
Ce schéma peut résoudre des distributions connues telles que la distribution Beta, Gamma, Logistique, Lognormale et autres [3 ].

Le calcul de l'eCDF est une tâche fastidieuse lorsque la prédiction est non paramétrique, ou plus précisément - la prédiction est une série de simulations. Mais le SDRC peut aussi s'exprimer comme suit :

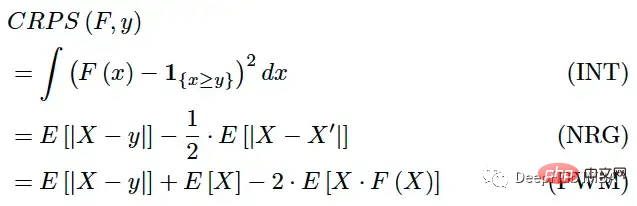
où X, X' sont des F indépendamment et distribués de manière identique. Ces expressions sont plus faciles à calculer, même si elles nécessitent néanmoins quelques calculs.

Implémentation Python

import numpy as np
 
 
 # Adapted to numpy from pyro.ops.stats.crps_empirical
 # Copyright (c) 2017-2019 Uber Technologies, Inc.
 # SPDX-License-Identifier: Apache-2.0
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 diff = y_pred[1:] - y_pred[:-1]
 weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1)
 weight = np.expand_dims(weight, -1)
 
 per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2
 return np.average(per_obs_crps, weights=sample_weight)

Fonction CRPS implémentée selon le formulaire NRG [2]. Adapté de pyroppl[6]

import numpy as np
 
 
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 b0 = y_pred.mean(axis=0)
 b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1))
 b1 = b1_values.mean(axis=0) / num_samples
 
 per_obs_crps = absolute_error + b0 - 2 * b1
 return np.average(per_obs_crps, weights=sample_weight)

Le code ci-dessus implémente CRPS basé sur le formulaire PWM[2].

Résumé

Le score de probabilité classé continu (CRPS) est une fonction de notation qui compare une seule valeur vraie à sa distribution prédite. Cette propriété le rend pertinent pour l’apprentissage automatique bayésien, où les modèles génèrent généralement des prédictions de distribution plutôt que des estimations ponctuelles. Cela peut être considéré comme une généralisation du célèbre MAE pour la prédiction de la distribution.

Il dispose d'expressions analytiques pour les prédictions paramétriques et permet des calculs simples pour les prédictions non paramétriques. Le CRPS pourrait devenir la nouvelle méthode standard pour évaluer les performances des modèles d’apprentissage automatique bayésiens avec des objectifs continus.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!