Périphériques technologiques
Périphériques technologiques
 IA
IA
 Articles très appréciés par les évaluateurs lors de la phase d'évaluation à l'aveugle de l'ICLR : s'agira-t-il d'une innovation majeure dans l'architecture Transformer ?
Articles très appréciés par les évaluateurs lors de la phase d'évaluation à l'aveugle de l'ICLR : s'agira-t-il d'une innovation majeure dans l'architecture Transformer ?
Articles très appréciés par les évaluateurs lors de la phase d'évaluation à l'aveugle de l'ICLR : s'agira-t-il d'une innovation majeure dans l'architecture Transformer ?
Malgré de nombreuses réalisations notables, les progrès pratiques dans la formation des réseaux de neurones profonds (DNN) ont été largement indépendants des bases théoriques. La plupart des DNN modernes à succès reposent sur des arrangements spécifiques de connexions résiduelles et de couches de normalisation, mais les principes généraux d'utilisation de ces composants dans les nouvelles architectures sont encore inconnus et leur rôle dans les architectures existantes n'est pas encore entièrement compris.
Les architectures résiduelles sont les plus populaires et les plus réussies, développées à l'origine dans le contexte des réseaux de neurones convolutifs (CNN), qui ont ensuite donné naissance à l'architecture de transformateur omniprésente des réseaux d'attention. L'une des raisons du succès des architectures résiduelles est une meilleure propagation du signal par rapport aux DNN ordinaires, où la propagation du signal fait référence à la transmission d'informations géométriques à travers les couches DNN et est représentée par une fonction de noyau.
Récemment, l'utilisation des principes de propagation du signal pour former des DNN plus profonds sans l'implication de connexions résiduelles et/ou de couches de normalisation dans les architectures résiduelles est devenue un domaine d'intérêt communautaire. Les raisons sont doubles : premièrement, cela valide l'hypothèse de propagation du signal pour l'efficacité des architectures résiduelles, élucidant ainsi la compréhension de l'interprétabilité du DNN ; deuxièmement, cela peut permettre des principes généraux et des méthodes pour l'entraînement du DNN au-delà du paradigme résiduel ;
Pour les CNN, les travaux de Xiao et al. (2018) montrent qu'une propagation améliorée du signal grâce à une meilleure initialisation peut entraîner efficacement les réseaux profonds ordinaires, bien qu'à une vitesse nettement plus lente que les réseaux résiduels. Les travaux de Martens et al. (2021) ont proposé le Deep Kernel Shaping (DKS), qui utilise la transformation de la fonction d'activation pour contrôler la propagation du signal, et utilise des optimiseurs puissants de second ordre tels que K-FAC pour mettre en œuvre la formation des réseaux ordinaires et des réseaux résiduels. sur ImageNet, les vitesses sont égales. Les travaux de Zhang et al. (2022) étendent le DKS à une classe plus large de fonctions d'activation et atteignent une quasi-égalité en généralisation.
La quantité clé à analyser dans la propagation du signal est le noyau du temps d'initialisation du DNN, ou plus précisément, le noyau approximatif sous la limite de largeur infinie. Pour les perceptrons multicouches (MLP) et les CNN utilisant l'initialisation delta, le noyau peut être écrit comme une simple récursion de couche contenant uniquement des fonctions 2D pour faciliter une analyse simple. L'évolution du noyau des transformateurs multicouches est plus complexe, de sorte que les méthodes existantes telles que DKS ne conviennent pas aux transformateurs ni même à toute architecture contenant des couches d'auto-attention.
Dans MLP, la propagation du signal est jugée en examinant le comportement des noyaux (unidimensionnels), tandis que la propagation du signal dans les transformateurs peut être jugée en examinant l'évolution des matrices de noyau (de haute dimension) dans les couches du réseau.
Cette recherche doit éviter une situation dans laquelle les éléments diagonaux grandissent ou rétrécissent rapidement avec l'augmentation de la profondeur, ce qui est lié à des normes d'activation incontrôlées et peut conduire à une perte de saturation ou à des problèmes numériques. Il est nécessaire d’éviter l’effondrement des rangs pour permettre la formation des transformateurs profonds, tandis que la question de savoir si des transformateurs profonds sans résidus peuvent être formés reste une question ouverte.
Cet article de l'étape d'examen à l'aveugle de l'ICLR 2023 résout ce problème et démontre pour la première fois qu'il est possible de former avec succès des transformateurs profonds sans connexions résiduelles ni couches de normalisation. À cette fin, ils étudient les problèmes de propagation du signal et d’effondrement des rangs dans les transformateurs profonds sans résidus et en dérivent trois méthodes pour les éviter. Plus précisément, l'approche utilise une combinaison d'initialisation de paramètres, de matrices de biais et de redimensionnement dépendant de la position, et met en évidence plusieurs complexités spécifiques à la propagation du signal dans les transformateurs, notamment les interactions avec le codage de position et le masquage causal. Les chercheurs ont démontré empiriquement que leur méthode peut générer des transformateurs profonds et sans résidus pouvant être entraînés.
Dans la partie expérimentale, sur les ensembles de données WikiText-103 et C4, les chercheurs ont démontré qu'en utilisant leur méthode principale, l'attention exponentielle de préservation du signal (E-SPA), peut être prolongée d'environ cinq fois le temps d'entraînement. perte du transformateur étalon comparable à celle du transformateur résiduel dans le papier. De plus, en combinant cette méthode avec des connexions résiduelles, les chercheurs ont également montré que les transformateurs sans couches de normalisation peuvent atteindre des vitesses d'entraînement comparables à celles des transformateurs standards.

Adresse papier : https://openreview.net/pdf?id=NPrsUQgMjKK
Pour cet article, l'ingénieur en chef de Google AI, Rohan Anil, estime qu'il s'agit d'un pas en avant pour l'architecture Transformer. . Un grand pas, ou une amélioration fondamentale.

Construire un transformateur profond qui peut être entraîné sans raccourcis
Jusqu'à présent, la seule stratégie pour corriger l'effondrement du rang du transformateur repose sur des connexions résiduelles, qui ignorent les problèmes inhérents à l'entraînement des couches d'auto-attention. En revanche, cette étude aborde directement cette question. Mieux comprendre d’abord la propagation du signal à travers les couches d’attention, puis modifier en fonction des informations obtenues pour obtenir une transmission fidèle du signal dans des transformateurs profonds, qui peuvent être entraînés avec ou sans connexions résiduelles.
Plus précisément, d'abord, l'étude a mené un réglage simple d'un transformateur vanille profond avec seulement une attention particulière, puis ils ont supposé que le transformateur avait un réglage à une tête (h = 1) ou un réglage à plusieurs têtes, où le la matrice d’attention A ne change pas entre les têtes. Si le bloc l ≤ L a une matrice d'attention A_l lors de l'initialisation, la représentation du bloc final est
peut être orthogonale lors de l'initialisation.
Sous les hypothèses ci-dessus, si 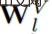 est utilisé pour représenter la matrice du noyau d'entrée à positions croisées, après quelques traitements de simplification, la formule suivante peut être obtenue :
est utilisé pour représenter la matrice du noyau d'entrée à positions croisées, après quelques traitements de simplification, la formule suivante peut être obtenue : 
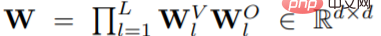 De cette formule simplifiée (profondeur attention uniquement à la matrice du noyau du transformateur), trois exigences pour (A_l)_l peuvent être déterminées :
De cette formule simplifiée (profondeur attention uniquement à la matrice du noyau du transformateur), trois exigences pour (A_l)_l peuvent être déterminées :
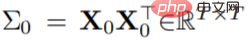 doit bien fonctionner dans chaque bloc, en évitant les situations dégénérées telles que l'effondrement des rangs et l'explosion/disparition des valeurs diagonales ; doit être ∀l non négatif au niveau des éléments ;
doit bien fonctionner dans chaque bloc, en évitant les situations dégénérées telles que l'effondrement des rangs et l'explosion/disparition des valeurs diagonales ; doit être ∀l non négatif au niveau des éléments ;
A_l doit être un ∀l triangulaire inférieur pour être compatible avec l'attention du masque causal. 
Dans les sections suivantes 3.1 et 3.2, la recherche se concentre sur la recherche d'une matrice d'attention qui répond aux besoins ci-dessus, et propose 3 méthodes E-SPA, U-SPA et Value-Skipinit, chaque méthode La matrice d'attention utilisée le contrôle du transformateur permet une propagation fidèle du signal même à de grandes profondeurs. De plus, la section 3.3 montre comment modifier l'attention softmax pour implémenter ces matrices d'attention.
-
 Dans la figure ci-dessous, l'étude a vérifié les deux schémas SPA proposés, U-SPA et E-SPA. Les résultats montrent qu'elle peut éviter avec succès l'attention des transformateurs vanille, même lorsque le réseau est en proie à un phénomène d'effondrement profond. .
Dans la figure ci-dessous, l'étude a vérifié les deux schémas SPA proposés, U-SPA et E-SPA. Les résultats montrent qu'elle peut éviter avec succès l'attention des transformateurs vanille, même lorsque le réseau est en proie à un phénomène d'effondrement profond. .
Expériences
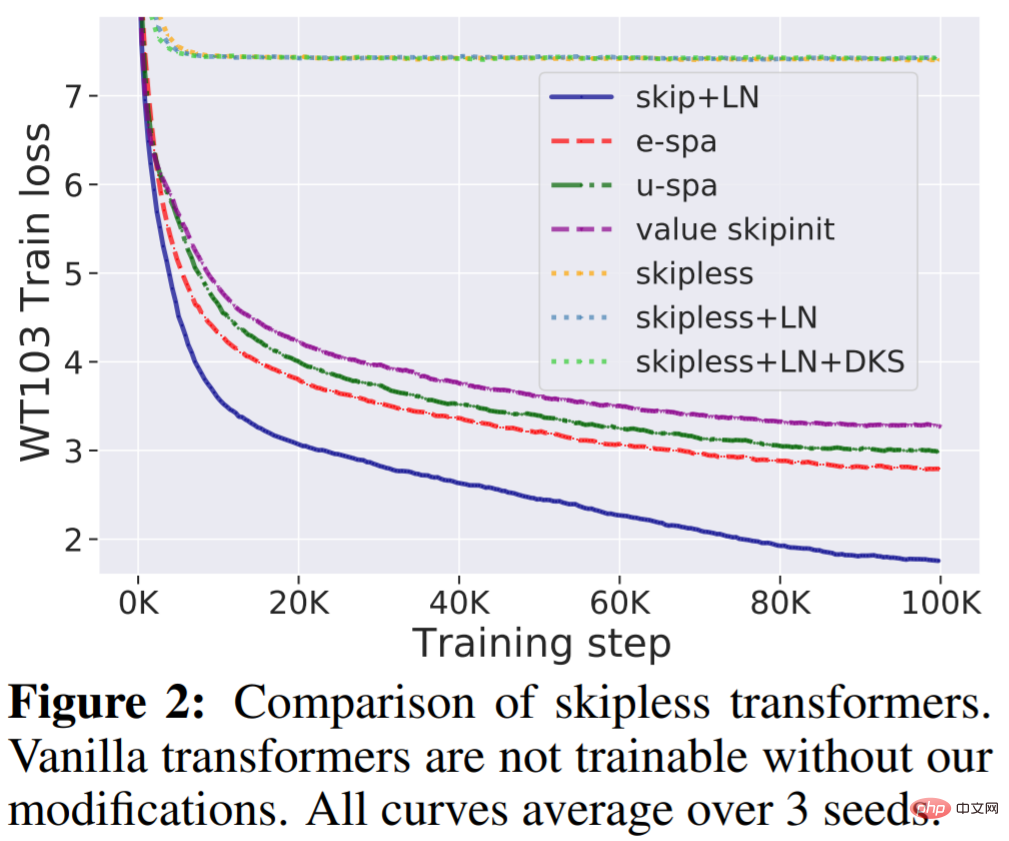
WikiText-103 Baseline : Premièrement, cette étude vérifie que les transformateurs profonds standards sans connexions résiduelles ne peuvent pas être entraînés, même s'ils ont des couches de normalisation (LN) et des activations transformées, mais notre méthode peut résoudre cette question. Comme le montre la figure 2, il est clairement visible que la suppression de la connexion résiduelle du transformateur standard le rend impossible à entraîner et la perte d'entraînement se stabilise à environ 7,5. Comme le montre la figure 1, le transformateur standard souffre d'un effondrement de rang.

En revanche, la méthode E-SPA proposée dans cette étude surpasse l'U-SPA et Value-Skipinit. Cependant, le transformateur par défaut avec résidu et LN conserve toujours l'avantage de la vitesse d'entraînement par rapport à notre méthode sans résidu.
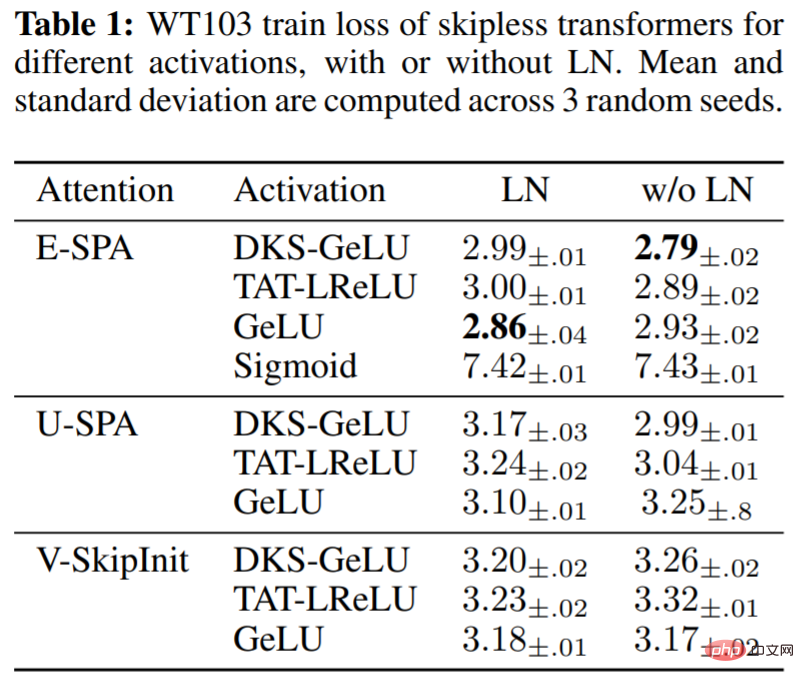
Dans le tableau 1, l'étude évalue l'impact des différentes fonctions d'activation dans le bloc MLP en utilisant la méthode proposée, ainsi que l'utilisation de LN dans le transformateur sans résidu. On peut voir qu'à la profondeur 36, notre méthode obtient de bonnes performances d'entraînement pour une série d'activations: GeLU transformé par DKS, Leaky ReLU transformé par TAT et GeLU non transformé, mais pas Sigmoïde non transformé. Il a également été constaté expérimentalement que la normalisation des couches est relativement peu importante pour la vitesse d'entraînement et peut même être préjudiciable à l'activation transformée lors de l'utilisation de SPA, qui dispose déjà de mécanismes intégrés pour contrôler les spécifications d'activation.

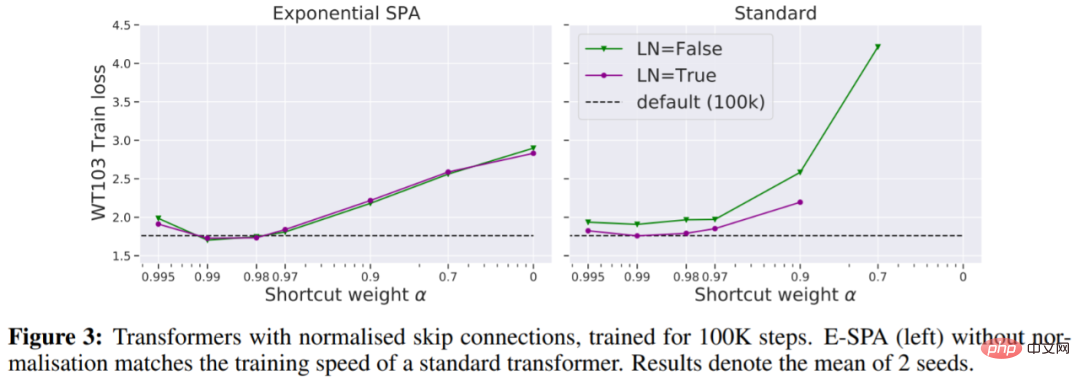
Dans la figure 3, nous voyons qu'une façon de faire correspondre la perte d'entraînement par défaut du transformateur sans nécessiter plus d'itérations consiste à utiliser une connexion résiduelle normalisée.

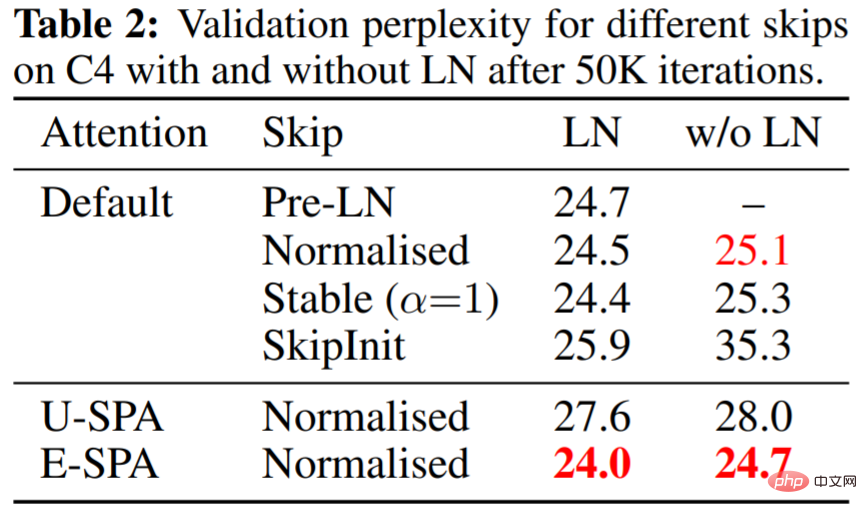
Le tableau 2 montre que l'E-SPA avec des résidus normalisés et du LN surpasse le transformateur PreLN par défaut.

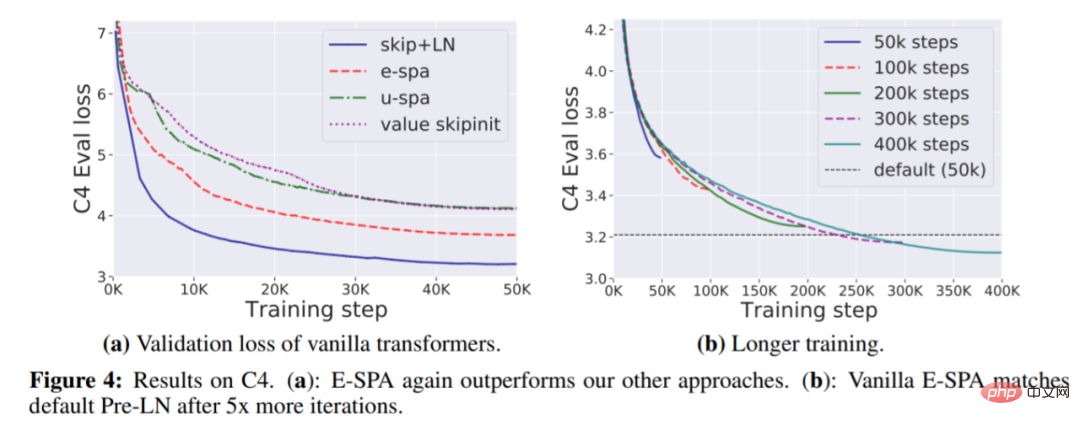
La figure 4(a) ci-dessous montre que l'E-SPA surpasse encore une fois les autres méthodes ; 4(b) montre que l'écart de perte d'entraînement peut être éliminé en augmentant simplement le temps d'entraînement.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
0. À quoi sert cet article ? Nous proposons DepthFM : un modèle d'estimation de profondeur monoculaire génératif de pointe, polyvalent et rapide. En plus des tâches traditionnelles d'estimation de la profondeur, DepthFM démontre également des capacités de pointe dans les tâches en aval telles que l'inpainting en profondeur. DepthFM est efficace et peut synthétiser des cartes de profondeur en quelques étapes d'inférence. Lisons ce travail ensemble ~ 1. Titre des informations sur l'article : DepthFM : FastMonocularDepthEstimationwithFlowMatching Auteur : MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 Abandonnez l'architecture codeur-décodeur et utilisez le modèle de diffusion pour la détection des contours avec de meilleurs résultats. L'Université nationale de technologie de la défense a proposé DiffusionEdge.
Feb 07, 2024 pm 10:12 PM
Abandonnez l'architecture codeur-décodeur et utilisez le modèle de diffusion pour la détection des contours avec de meilleurs résultats. L'Université nationale de technologie de la défense a proposé DiffusionEdge.
Feb 07, 2024 pm 10:12 PM
Les réseaux actuels de détection des contours profonds adoptent généralement une architecture d'encodeur-décodeur, qui contient des modules d'échantillonnage ascendant et descendant pour mieux extraire les fonctionnalités à plusieurs niveaux. Cependant, cette structure limite le réseau à produire des résultats de détection de contour précis et détaillés. En réponse à ce problème, un article sur AAAI2024 propose une nouvelle solution. Titre de la thèse : DiffusionEdge : DiffusionProbabilisticModelforCrispEdgeDetection Auteurs : Ye Yunfan (Université nationale de technologie de la défense), Xu Kai (Université nationale de technologie de la défense), Huang Yuxing (Université nationale de technologie de la défense), Yi Renjiao (Université nationale de technologie de la défense), Cai Zhiping (Université nationale de technologie de la défense) Lien vers l'article : https ://ar
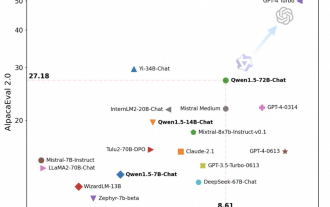 Tongyi Qianwen est à nouveau open source, Qwen1.5 propose six modèles de volume et ses performances dépassent GPT3.5
Feb 07, 2024 pm 10:15 PM
Tongyi Qianwen est à nouveau open source, Qwen1.5 propose six modèles de volume et ses performances dépassent GPT3.5
Feb 07, 2024 pm 10:15 PM
À temps pour la Fête du Printemps, la version 1.5 du modèle Tongyi Qianwen (Qwen) est en ligne. Ce matin, la nouvelle de la nouvelle version a attiré l'attention de la communauté IA. La nouvelle version du grand modèle comprend six tailles de modèle : 0,5B, 1,8B, 4B, 7B, 14B et 72B. Parmi eux, les performances de la version la plus puissante surpassent GPT3.5 et Mistral-Medium. Cette version inclut le modèle de base et le modèle Chat et fournit une prise en charge multilingue. L'équipe Tongyi Qianwen d'Alibaba a déclaré que la technologie pertinente avait également été lancée sur le site officiel de Tongyi Qianwen et sur l'application Tongyi Qianwen. De plus, la version actuelle de Qwen 1.5 présente également les points forts suivants : prend en charge une longueur de contexte de 32 Ko ; ouvre le point de contrôle du modèle Base+Chat ;
 Les grands modèles peuvent également être découpés, et Microsoft SliceGPT augmente considérablement l'efficacité de calcul de LAMA-2.
Jan 31, 2024 am 11:39 AM
Les grands modèles peuvent également être découpés, et Microsoft SliceGPT augmente considérablement l'efficacité de calcul de LAMA-2.
Jan 31, 2024 am 11:39 AM
Les grands modèles de langage (LLM) comportent généralement des milliards de paramètres et sont formés sur des milliards de jetons. Cependant, ces modèles sont très coûteux à former et à déployer. Afin de réduire les besoins de calcul, diverses techniques de compression de modèles sont souvent utilisées. Ces techniques de compression de modèles peuvent généralement être divisées en quatre catégories : distillation, décomposition tensorielle (y compris la factorisation de bas rang), élagage et quantification. Les méthodes d'élagage existent depuis un certain temps, mais beaucoup nécessitent un réglage fin de la récupération (RFT) après l'élagage pour maintenir les performances, ce qui rend l'ensemble du processus coûteux et difficile à faire évoluer. Des chercheurs de l'ETH Zurich et de Microsoft ont proposé une solution à ce problème appelée SliceGPT. L'idée principale de cette méthode est de réduire l'intégration du réseau en supprimant des lignes et des colonnes dans la matrice de pondération.
 Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas entre officiellement dans l’ère des robots électriques ! Hier, l'Atlas hydraulique s'est retiré "en larmes" de la scène de l'histoire. Aujourd'hui, Boston Dynamics a annoncé que l'Atlas électrique était au travail. Il semble que dans le domaine des robots humanoïdes commerciaux, Boston Dynamics soit déterminé à concurrencer Tesla. Après la sortie de la nouvelle vidéo, elle a déjà été visionnée par plus d’un million de personnes en seulement dix heures. Les personnes âgées partent et de nouveaux rôles apparaissent. C'est une nécessité historique. Il ne fait aucun doute que cette année est l’année explosive des robots humanoïdes. Les internautes ont commenté : Les progrès des robots ont fait ressembler la cérémonie d'ouverture de cette année à des êtres humains, et le degré de liberté est bien plus grand que celui des humains. Mais n'est-ce vraiment pas un film d'horreur ? Au début de la vidéo, Atlas est allongé calmement sur le sol, apparemment sur le dos. Ce qui suit est à couper le souffle
 Point Transformer mis à jour : plus efficace, plus rapide et plus puissant !
Jan 17, 2024 am 08:27 AM
Point Transformer mis à jour : plus efficace, plus rapide et plus puissant !
Jan 17, 2024 am 08:27 AM
Titre original : PointTransformerV3 : Simpler, Faster, Stronger Lien article : https://arxiv.org/pdf/2312.10035.pdf Lien code : https://github.com/Pointcept/PointTransformerV3 Unité auteur : HKUSHAILabMPIPKUMIT Idée article : Cet article est non destiné à être publié dans À la recherche de l’innovation au sein du mécanisme d’attention. Au lieu de cela, il se concentre sur l’exploitation de la puissance de l’échelle pour surmonter les compromis existants entre précision et efficacité dans le contexte du traitement des nuages de points. S'inspirer des avancées récentes en matière d'apprentissage des représentations 3D à grande échelle,
 La version Kuaishou de Sora 'Ke Ling' est ouverte aux tests : génère plus de 120 s de vidéo, comprend mieux la physique et peut modéliser avec précision des mouvements complexes
Jun 11, 2024 am 09:51 AM
La version Kuaishou de Sora 'Ke Ling' est ouverte aux tests : génère plus de 120 s de vidéo, comprend mieux la physique et peut modéliser avec précision des mouvements complexes
Jun 11, 2024 am 09:51 AM
Quoi? Zootopie est-elle concrétisée par l’IA domestique ? Avec la vidéo est exposé un nouveau modèle de génération vidéo domestique à grande échelle appelé « Keling ». Sora utilise une voie technique similaire et combine un certain nombre d'innovations technologiques auto-développées pour produire des vidéos qui comportent non seulement des mouvements larges et raisonnables, mais qui simulent également les caractéristiques du monde physique et possèdent de fortes capacités de combinaison conceptuelle et d'imagination. Selon les données, Keling prend en charge la génération de vidéos ultra-longues allant jusqu'à 2 minutes à 30 ips, avec des résolutions allant jusqu'à 1080p, et prend en charge plusieurs formats d'image. Un autre point important est que Keling n'est pas une démo ou une démonstration de résultats vidéo publiée par le laboratoire, mais une application au niveau produit lancée par Kuaishou, un acteur leader dans le domaine de la vidéo courte. De plus, l'objectif principal est d'être pragmatique, de ne pas faire de chèques en blanc et de se mettre en ligne dès sa sortie. Le grand modèle de Ke Ling est déjà sorti à Kuaiying.
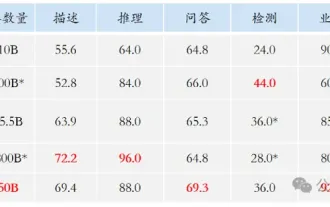 La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
Je pleure à mort. Le monde construit à la folie de grands modèles. Les données sur Internet ne suffisent pas du tout. Le modèle de formation ressemble à « The Hunger Games », et les chercheurs en IA du monde entier se demandent comment nourrir ces personnes avides de données. Ce problème est particulièrement important dans les tâches multimodales. À une époque où rien ne pouvait être fait, une équipe de start-up du département de l'Université Renmin de Chine a utilisé son propre nouveau modèle pour devenir la première en Chine à faire de « l'auto-alimentation des données générées par le modèle » une réalité. De plus, il s’agit d’une approche à deux volets, du côté compréhension et du côté génération, les deux côtés peuvent générer de nouvelles données multimodales de haute qualité et fournir un retour de données au modèle lui-même. Qu'est-ce qu'un modèle ? Awaker 1.0, un grand modèle multimodal qui vient d'apparaître sur le Forum Zhongguancun. Qui est l'équipe ? Moteur Sophon. Fondé par Gao Yizhao, doctorant à la Hillhouse School of Artificial Intelligence de l’Université Renmin.



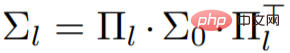 Dans la figure ci-dessous, l'étude a vérifié les deux schémas SPA proposés, U-SPA et E-SPA. Les résultats montrent qu'elle peut éviter avec succès l'attention des transformateurs vanille, même lorsque le réseau est en proie à un phénomène d'effondrement profond. .
Dans la figure ci-dessous, l'étude a vérifié les deux schémas SPA proposés, U-SPA et E-SPA. Les résultats montrent qu'elle peut éviter avec succès l'attention des transformateurs vanille, même lorsque le réseau est en proie à un phénomène d'effondrement profond. .