

Partie 01
weightQu'est-ce que l'intégration d'images Quantity
L'intégration de graphiques est la cartographie de la structure du graphique données Il s'agit d'un processus de vecteurs denses de basse dimension, et en même temps, les nœuds avec des structures topologiques similaires ou des attributs proches dans le graphe d'origine sont également proches en position dans l'espace vectoriel, ce qui peut bien résoudre le problème que représente le graphe- les données structurées sont difficiles à saisir efficacement dans les algorithmes d’apprentissage automatique.
Pour la représentation et le stockage de graphiques, la façon la plus simple de penser est d'utiliser la matrice de contiguïté. Numérotez chaque nœud du graphique pour construire une matrice de  , où
, où 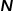 représente le nombre de nœuds dans le graphique. Le fait que deux nœuds du graphique soient connectés par une arête détermine la valeur de la position correspondante dans la matrice de contiguïté. Cette méthode de représentation est très facile à comprendre et intuitive, mais elle est très inefficace. Étant donné que les graphiques dans des scénarios réels peuvent contenir des milliers de nœuds, voire plus, et que la plupart des nœuds ne sont pas connectés par des arêtes, la matrice de contiguïté résultante sera très clairsemée. L'utilisation de matrices de contiguïté pour représenter et stocker des graphiques nécessite des coûts de calcul et d'espace élevés, tandis que les algorithmes d'intégration de graphiques peuvent résoudre efficacement les problèmes d'analyse de graphiques.
représente le nombre de nœuds dans le graphique. Le fait que deux nœuds du graphique soient connectés par une arête détermine la valeur de la position correspondante dans la matrice de contiguïté. Cette méthode de représentation est très facile à comprendre et intuitive, mais elle est très inefficace. Étant donné que les graphiques dans des scénarios réels peuvent contenir des milliers de nœuds, voire plus, et que la plupart des nœuds ne sont pas connectés par des arêtes, la matrice de contiguïté résultante sera très clairsemée. L'utilisation de matrices de contiguïté pour représenter et stocker des graphiques nécessite des coûts de calcul et d'espace élevés, tandis que les algorithmes d'intégration de graphiques peuvent résoudre efficacement les problèmes d'analyse de graphiques.
Partie 02
weight Concept de base Quantity
Concept 1 Photo :
Le graphique est représenté par 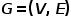 , où
, où 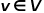 représente les nœuds et
représente les nœuds et 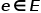 représente les arêtes.
représente les arêtes. 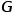 est associée à la fonction de mappage de type de nœud
est associée à la fonction de mappage de type de nœud 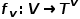 et à la fonction de mappage de type de bord
et à la fonction de mappage de type de bord 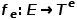 .
. 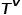 représente un ensemble de types de nœuds et
représente un ensemble de types de nœuds et 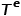 représente un ensemble de types d'arêtes.
représente un ensemble de types d'arêtes.
Concept 2 Graphique isomorphe :
graphique 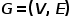 , où
, où 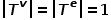 . C'est-à-dire que tous les nœuds appartiennent à un type et tous les bords appartiennent à un seul type. Par exemple, le graphe de relation d'attention de l'utilisateur dans un réseau social n'a qu'un seul type de nœud, l'utilisateur, et un seul type de bord, la relation d'attention.
. C'est-à-dire que tous les nœuds appartiennent à un type et tous les bords appartiennent à un seul type. Par exemple, le graphe de relation d'attention de l'utilisateur dans un réseau social n'a qu'un seul type de nœud, l'utilisateur, et un seul type de bord, la relation d'attention.
Concept 3 Graphique hétérogène :
graphique 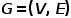 , où
, où 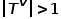 ou
ou 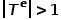 . C'est-à-dire qu'il existe plusieurs types de nœuds ou types de bords. Par exemple, dans la structure graphique d'un réseau universitaire, il existe plusieurs types de nœuds tels que les articles, les auteurs, les conférences, etc. Les relations de bord incluent la relation créative. entre les auteurs et les articles, les articles et les conférences, la relation de publication entre eux, la relation de citation entre les articles, etc.
. C'est-à-dire qu'il existe plusieurs types de nœuds ou types de bords. Par exemple, dans la structure graphique d'un réseau universitaire, il existe plusieurs types de nœuds tels que les articles, les auteurs, les conférences, etc. Les relations de bord incluent la relation créative. entre les auteurs et les articles, les articles et les conférences, la relation de publication entre eux, la relation de citation entre les articles, etc.
Concept 4 Similitude de premier ordre :
Si le poids de l'arête reliant deux nœuds est plus grand, la similarité de premier ordre entre eux est plus grande. La similarité de premier ordre entre le nœud 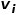 et le nœud
et le nœud 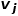 s'exprime par
s'exprime par 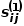 , il y a
, il y a 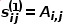 , où est le nœud
, où est le nœud 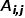 et nœuds Le poids des bords
et nœuds Le poids des bords 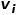 entre
entre 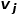 .
.  Concept 5 Similitude de second ordre :
Concept 5 Similitude de second ordre :
Si les structures de réseau de deux nœuds adjacents sont plus similaires, plus la similarité de second ordre entre eux est grande. La similarité de second ordre
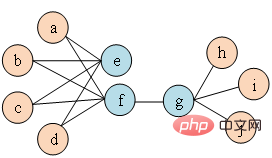
et le nœud Figure 1 Diagramme schématique de similarité du second ordre Concept 6 Incorporation de graphe : Étant donné le graphe d'entrée et les dimensions d'intégration prédéfinies, l'intégration de graphe doit être aussi efficace que possible Convertissez le graphique en espace dimensionnel tout en conservant les propriétés du graphique. S'appuyer sur la similarité du premier ordre ou la similarité d'ordre supérieur pour quantifier le degré de préservation des propriétés du graphe, en utilisant un vecteur dimensionnel ou un ensemble de Partie 03 weight Classification des algorithmes d'intégration de graphiques Quantity Au cours des dernières décennies , les chercheurs ont proposé de nombreux excellents algorithmes, dont il a été prouvé qu'ils ont des effets significatifs sur les réseaux sociaux, les réseaux de communication et d'autres scénarios. L'industrie divise généralement ces algorithmes d'intégration de graphiques dans les trois catégories suivantes en fonction des différences de granularité de sortie : (1) Incorporation de nœuds L'intégration de nœuds est le type le plus courant, utilisant des vecteurs en faible espace dimensionnel Représentant chaque nœud du graphique, les représentations vectorielles d'intégration des nœuds « similaires » sont également similaires. Lorsqu'il est nécessaire d'analyser les nœuds dans le graphique, puis d'effectuer des tâches telles que la classification ou le clustering de nœuds, l'intégration de nœuds est généralement choisie. (2) L'intégration des bords utilise un vecteur pour représenter chaque arête du graphique dans un espace de faible dimension. Une arête est constituée d’une paire de nœuds, représentant généralement une relation nœud-paire. L'intégration des bords convient lorsque vous devez analyser les bords du graphique et effectuer des tâches telles que la prédiction de relations dans un graphe de connaissances ou la prédiction de liens. (3) L'intégration de graphiques utilise des vecteurs pour représenter l'ensemble du graphique dans un espace de faible dimension, généralement un petit graphique tel qu'une molécule ou une protéine. La représentation d'un graphique sous forme de vecteur facilite le calcul des similitudes entre différents graphiques, résolvant ainsi les problèmes de classification des graphiques. Différentes exigences de tâche déterminent l'algorithme d'intégration de graphique sélectionné. Pour des raisons d'espace, l'algorithme DeepWalk et l'algorithme Node2Vec dans l'intégration de nœuds sont extraits ici pour un apprentissage relativement détaillé. Partie 04 weight Quantity 1.Algorithme DeepWalk Inspiré par l'idée de word2vec dans le domaine de traitement du langage naturel, Perozzi et al. ont proposé DeepWalk afin d'établir un modèle d'apprentissage des vecteurs de représentation des nœuds dans le graphe et d'analoguer la relation de co-occurrence entre les nœuds à la relation de co-occurrence entre les mots dans l'algorithme du corpus. La séquence de nœuds voisins dans le graphe est collectée via des marches aléatoires, ce qui équivaut à un corpus de contexte de nœud, et peut ainsi résoudre le problème de l'extraction des relations de cooccurrence entre les nœuds du graphe. Définissez à l'avance la longueur et le point de départ de la séquence de nœuds. La stratégie de marche aléatoire guidera la façon de déterminer le prochain nœud de marche parmi les nœuds voisins. Répétez cette étape pour obtenir une séquence qui répond aux conditions. Le diagramme de marche aléatoire est présenté dans la figure. 2. Montrez. Figure 2 Diagramme schématique de la marche aléatoire Les mots de l'algorithme word2vec correspondent aux nœuds du graphique Afin d'apprendre davantage la représentation des caractéristiques latentes des nœuds, l'algorithme DeepWalk introduit la fonction de mappage Le calcul de probabilité doit également faire référence au modèle skip-gram dans l'algorithme word2vec. Comme le montre la figure 3, le modèle skip-gram contient deux matrices clés, l'une est la matrice vectorielle de mots centrale Dans le processus de marche aléatoire, la relation séquentielle entre les nœuds dans la séquence d'échantillonnage n'est pas prise en compte, ce qui peut mieux refléter la relation de proximité des nœuds et réduire le coût de calcul. Figure 3 Diagramme du modèle Skip-gram 2. Basé sur l'algorithme DeepWalk, les chercheurs Grover A et Leskovec J ont proposé l'algorithme Node2Vec. L'algorithme Node2Vec optimise le processus de génération de séquences de nœuds via des marches aléatoires dans l'algorithme DeepWalk. Il définit les paramètres où Figure 4 Diagramme schématique de la stratégie de marche aléatoire Node2Vec Node2Vec est contrôlée en fonction de deux paramètres, comme le montre la figure 4. Supposons que le nœud v soit atteint via le bord , renvoie le nœud (2) Lorsque (3) Lorsque En d'autres termes, le paramètre Partie 05 weightRésumé Avec le développement rapide des technologies de l'information, l'environnement réseau est devenu de plus en plus complexe et les attaques réseau se produisent fréquemment. Parmi elles, les attaques APT sont fréquentes, ce qui constitue un problème de sécurité auquel les entreprises doivent prêter attention. En fait, le réseau, l'environnement de base dans lequel se produisent les attaques APT, est lui-même une structure de réseau composée d'ordinateurs et d'autres éléments. Il n'est pas difficile d'envisager d'utiliser des structures de données graphiques pour exprimer la relation entre ces éléments, puis de les transformer. problème de détection d'attaque dans une tâche de classification de nœud, de bord ou de sous-graphe dans un graphique. L'intégration de graphiques est une question riche avec un grand espace de recherche. Comment améliorer l'efficacité de la formation des modèles, innover dans les méthodes de construction de modèles et appliquer l'idée de l'intégration de graphiques à davantage de pratiques de production. Les entreprises ont besoin de recherches supplémentaires pour trouver de meilleures solutions. Références [1]Xu M. Comprendre les méthodes d'intégration de graphes et leurs applications[J]. [2]Cai H, Zheng VW, Chang KCC. Une étude complète de l'intégration de graphes : problèmes, techniques et applications[J] IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9) : 1616-1637.. [3]Goyal P, Ferrara E. Techniques, applications et performances d'intégration de graphiques : une enquête[J].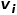 est le quartier
est le quartier 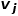 et de
et de 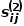 Quartiers de
Quartiers de 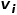 Similitudes entre
Similitudes entre 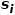 . Comme le montre la figure 1, comme il existe une arête reliant le nœud f et le nœud g, le nœud f et le nœud g sont similaires au premier ordre. Bien qu'il n'y ait pas de bord reliant le nœud e et le nœud g, ils ont quatre nœuds voisins identiques, donc le nœud e et le nœud g sont similaires au second ordre.
. Comme le montre la figure 1, comme il existe une arête reliant le nœud f et le nœud g, le nœud f et le nœud g sont similaires au premier ordre. Bien qu'il n'y ait pas de bord reliant le nœud e et le nœud g, ils ont quatre nœuds voisins identiques, donc le nœud e et le nœud g sont similaires au second ordre. 
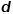 vecteurs dimensionnels pour représenter un graphe, chaque vecteur représentant l'incorporation d'une partie de le graphique, comme un nœud ou une arête.
vecteurs dimensionnels pour représenter un graphe, chaque vecteur représentant l'incorporation d'une partie de le graphique, comme un nœud ou une arête. 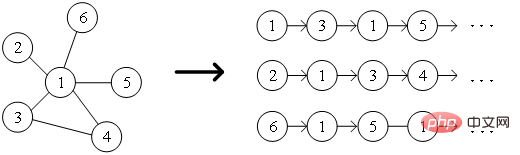
 , et la séquence de mots correspond à la séquence de nœuds obtenue par le marche aléatoire, puis pour Une marche aléatoire
, et la séquence de mots correspond à la séquence de nœuds obtenue par le marche aléatoire, puis pour Une marche aléatoire  définit sa fonction objectif d'optimisation comme indiqué dans la formule.
définit sa fonction objectif d'optimisation comme indiqué dans la formule. 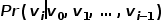
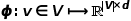 pour réaliser le mappage des nœuds dans le graphique aux vecteurs
pour réaliser le mappage des nœuds dans le graphique aux vecteurs 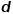 dimensionnels , alors le problème est transformé Pour estimer la probabilité de la formule suivante.
dimensionnels , alors le problème est transformé Pour estimer la probabilité de la formule suivante. 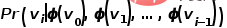
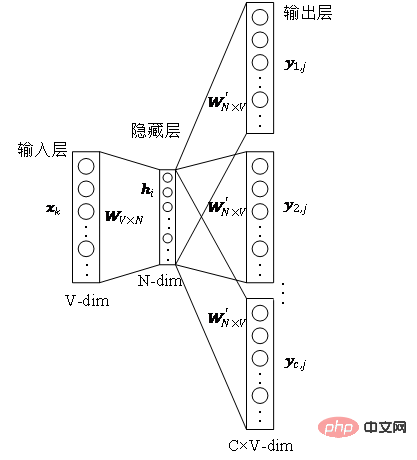
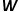 et l'autre est la matrice vectorielle de mots d'arrière-plan
et l'autre est la matrice vectorielle de mots d'arrière-plan  . Les matrices de poids représentent respectivement les vecteurs de mots associés aux mots comme différents rôles. Skip-gram est un modèle de prédiction du contexte des mots. Il apprend d'abord les relations entre les mots du corpus, puis utilise ces relations pour exprimer le contexte d'un mot spécifique, c'est-à-dire la représentation vectorielle du mot. C’est-à-dire que dans une même séquence, plus deux mots apparaissent fréquemment en même temps, plus les représentations vectorielles des deux mots sont similaires. Appliquez cette idée au graphique et définissez sa fonction objectif d'optimisation comme indiqué dans la formule.
. Les matrices de poids représentent respectivement les vecteurs de mots associés aux mots comme différents rôles. Skip-gram est un modèle de prédiction du contexte des mots. Il apprend d'abord les relations entre les mots du corpus, puis utilise ces relations pour exprimer le contexte d'un mot spécifique, c'est-à-dire la représentation vectorielle du mot. C’est-à-dire que dans une même séquence, plus deux mots apparaissent fréquemment en même temps, plus les représentations vectorielles des deux mots sont similaires. Appliquez cette idée au graphique et définissez sa fonction objectif d'optimisation comme indiqué dans la formule. 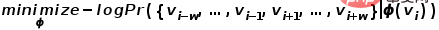
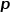 et les paramètres
et les paramètres 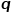 pour déterminer si chaque marche aléatoire a tendance à être un échantillonnage en largeur ou en profondeur. échantillonnage, donc l’adaptabilité est élevée. En supposant que le nœud
pour déterminer si chaque marche aléatoire a tendance à être un échantillonnage en largeur ou en profondeur. échantillonnage, donc l’adaptabilité est élevée. En supposant que le nœud 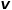 est actuellement visité, la probabilité de la prochaine visite du nœud
est actuellement visité, la probabilité de la prochaine visite du nœud 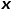 est celle indiquée dans la formule.
est celle indiquée dans la formule. 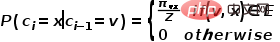
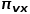 représente la probabilité de transition du nœud
représente la probabilité de transition du nœud 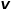 au nœud
au nœud 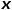 , et
, et 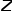 représente la constante de normalisation.
représente la constante de normalisation. 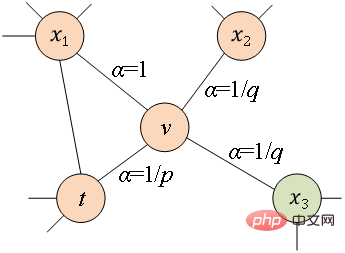
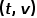 , et l'étape suivante consiste à visiter le nœud droit. Autrement dit, lorsque le graphe est un graphe non pondéré,
, et l'étape suivante consiste à visiter le nœud droit. Autrement dit, lorsque le graphe est un graphe non pondéré, 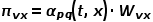 détermine directement la probabilité de transition du nœud. Lorsque le graphique est un graphique pondéré, le produit de
détermine directement la probabilité de transition du nœud. Lorsque le graphique est un graphique pondéré, le produit de 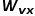 et le poids du bord
et le poids du bord 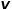 détermine la probabilité de transition finale du nœud.
détermine la probabilité de transition finale du nœud. 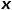 peut être calculé selon la formule suivante, où
peut être calculé selon la formule suivante, où 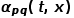 est la distance de chemin la plus courte entre le nœud
est la distance de chemin la plus courte entre le nœud 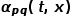 et le nœud
et le nœud 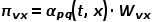 .
. 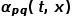 Lorsque l'échantillon errant passe du nœud
Lorsque l'échantillon errant passe du nœud 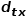 au nœud
au nœud 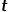 et doit sélectionner le nœud de saut suivant, les trois situations suivantes se présenteront.
et doit sélectionner le nœud de saut suivant, les trois situations suivantes se présenteront. 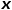 (1) Quand
(1) Quand 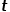 .
. 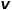
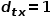 , sélectionnez le nœud adjacent commun du nœud
, sélectionnez le nœud adjacent commun du nœud 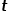 et du nœud
et du nœud 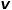 , tel que le nœud
, tel que le nœud 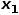 .
. 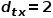 , sélectionnez le nœud adjacent du nœud
, sélectionnez le nœud adjacent du nœud 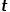 qui n'a rien à voir avec le nœud
qui n'a rien à voir avec le nœud 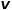 , tel que le nœud
, tel que le nœud 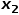 ou
ou 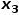 .
. 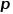 contrôle la probabilité de revenir au nœud du saut précédent, et le paramètre
contrôle la probabilité de revenir au nœud du saut précédent, et le paramètre 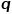 contrôle davantage s'il faut explorer les informations de structure locale ou les informations de structure globale. du réseau, DeepWalk Le modèle est en fait le modèle Node2Vec lorsque les valeurs de
contrôle davantage s'il faut explorer les informations de structure locale ou les informations de structure globale. du réseau, DeepWalk Le modèle est en fait le modèle Node2Vec lorsque les valeurs de 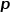 et
et 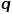 sont fixées à 1.
sont fixées à 1.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Promotion d'annonces
Promotion d'annonces
 Quel est le format du nom de compte de Steam
Quel est le format du nom de compte de Steam
 vim sauvegarder et quitter la commande
vim sauvegarder et quitter la commande
 Cinq raisons pour lesquelles votre ordinateur ne s'allume pas
Cinq raisons pour lesquelles votre ordinateur ne s'allume pas
 heure du système Linux
heure du système Linux
 Comment résoudre l'erreur 443
Comment résoudre l'erreur 443
 Où est le bouton d'impression ?
Où est le bouton d'impression ?
 Le rôle de la fonction parseint
Le rôle de la fonction parseint
 Que faire si l'installation du pilote de la carte son échoue
Que faire si l'installation du pilote de la carte son échoue