Comment générer de « bons » graphiques ? Examen systématique des modèles génératifs profonds pour la génération de graphiques

Les graphiques sont des représentations de données importantes qui décrivent les objets et leurs relations, et ils apparaissent dans une variété de scénarios réels. La génération de graphiques est l'un des problèmes clés dans ce domaine, qui consiste à apprendre la distribution d'un graphique donné et à générer davantage de nouveaux graphiques. Cependant, en raison de leurs applications répandues, les modèles génératifs de graphiques avec une histoire riche sont traditionnellement fabriqués à la main et ne peuvent modéliser que certaines propriétés statistiques des graphiques.

Les progrès récents dans les modèles génératifs profonds pour la génération de graphiques constituent une étape importante vers l'amélioration de la fidélité des graphiques générés et ouvrent la voie à de nouveaux types d'applications. Cet article fournit un aperçu détaillé de la littérature dans le domaine des modèles génératifs profonds pour la génération de graphes. Premièrement, la définition formelle et la connaissance préliminaire des modèles génératifs profonds pour la génération de graphes sont proposées ; deuxièmement, la classification des modèles génératifs profonds pour la génération de graphes inconditionnelle et conditionnelle est proposée respectivement et les travaux existants de chacun sont comparés et analysés ; Ensuite, un aperçu des paramètres d’évaluation dans ce domaine spécifique sera donné. Enfin, les applications de la génération de cartes de profondeur sont résumées et cinq directions de recherche prometteuses sont soulignées.

Introduction

Les graphiques sont omniprésents dans le monde réel, représentant les objets et leurs relations, tels que les réseaux sociaux, les réseaux de citations, les réseaux biologiques, les réseaux de transport, etc. Les graphiques sont également connus pour avoir des structures complexes contenant de riches valeurs sous-jacentes [1]. Des efforts importants ont été réalisés dans ce domaine, aboutissant à une littérature riche et à des méthodes permettant de traiter divers problèmes de graphes.

Ces tâches peuvent être divisées en deux catégories : 1) Prédire et analyser les modèles d'un graphique donné. 2) Apprenez la distribution d'un graphique donné et générez des graphiques plus nouveaux. Le premier type couvre de nombreux domaines de recherche, notamment la classification des nœuds, la classification des graphes et la prédiction des liens. De nombreux travaux ont été réalisés dans ce domaine au cours des dernières décennies. Par rapport au premier type de problèmes, le deuxième type de problèmes est lié aux problèmes de génération de graphes, qui font également l’objet de cet article.

La génération de graphiques comprend le processus de modélisation et de génération de graphiques du monde réel, qui a des applications dans plusieurs domaines, tels que la compréhension de la dynamique d'interaction dans les réseaux sociaux [2], [3], [4], la détection d'anomalies [ 5] , modélisation de la structure des protéines [6], [7], génération et traduction de code source [8], [9], analyse sémantique [10]. En raison de leur large application, le développement de modèles génératifs de graphes a une histoire riche, aboutissant à des modèles bien connus tels que les graphes aléatoires, les modèles de petit monde, les modèles de blocs stochastiques et les modèles de réseaux bayésiens, qui sont basés sur des modèles structurels a priori. hypothèses [11 ] Générer un graphique. Ces modèles générateurs de graphes [12], [13], [14] visent à modéliser des familles de graphes présélectionnées telles que les graphes aléatoires [15], les réseaux de petits mondes [16] et les graphes sans échelle [12]. Cependant, en raison de leur simplicité et de leur nature artisanale, ces modèles de graphes aléatoires ont souvent une capacité limitée à modéliser des dépendances complexes et ne peuvent modéliser que certaines propriétés statistiques du graphe.

Ces méthodes fonctionnent généralement bien pour les propriétés pour lesquelles les principes prédéfinis sont adaptés, mais ne fonctionnent souvent pas bien pour d'autres propriétés. Par exemple, les modèles de réseaux de contacts peuvent s’adapter aux épidémies de grippe mais pas à la connectivité fonctionnelle dynamique. Cependant, dans de nombreux domaines, la nature et les principes générateurs des réseaux sont largement inconnus, comme ceux qui expliquent les mécanismes de la maladie mentale, les cyberattaques et la propagation des logiciels malveillants dans les réseaux cérébraux. Pour un autre exemple, le graphique d'Erdos-Renyi n'a pas la distribution de degrés à queue lourde typique de nombreux réseaux du monde réel. De plus, l’utilisation d’hypothèses a priori empêche ces techniques traditionnelles d’explorer davantage d’applications dans des domaines à plus grande échelle où la connaissance a priori des graphiques est toujours indisponible.

Compte tenu des limites des techniques traditionnelles de génération de graphiques, un défi majeur consiste à développer des méthodes capables d'apprendre directement des modèles génératifs à partir d'une collection de graphiques observés, ce qui constitue une étape importante vers l'amélioration de la fidélité des graphiques générés. Cela ouvre la voie à de nouveaux types d’applications, telles que la découverte de nouveaux médicaments [17], [18] et la modélisation de la structure des protéines [19], [20], [21]. Des progrès récents dans les modèles génératifs profonds, tels que les auto-encodeurs variationnels (VAE) [22] et les réseaux contradictoires génératifs (GAN) [23], ont été proposés pour générer des graphiques. De nombreux modèles d'apprentissage profond ont été formalisés pour la génération de graphiques. modèles génératifs profonds, qui font l’objet de cette revue.

Divers travaux avancés ont été réalisés sur la génération de cartes approfondies, de la génération de graphiques ponctuels aux processus de génération de graphiques séquentiels, en s'adaptant à diverses stratégies d'apprentissage génératif profond. Ces méthodes visent à relever un ou plusieurs des défis ci-dessus en travaillant dans différents domaines, notamment l'apprentissage automatique, la bioinformatique, l'intelligence artificielle, la santé humaine et l'exploitation des réseaux sociaux. Cependant, les méthodes développées dans différents domaines de recherche utilisent souvent un vocabulaire différent et abordent les problèmes sous des angles différents.

De plus, il existe un manque de procédures d'évaluation standard et complètes pour valider les modèles génératifs profonds développés pour les graphiques. À cette fin, cet article propose une revue systématique des modèles génératifs profonds pour la génération de graphiques. L'objectif est d'aider les chercheurs interdisciplinaires à choisir les technologies appropriées pour résoudre les problèmes dans leurs domaines d'application et, plus important encore, d'aider les chercheurs en génération de graphes à comprendre les principes de base de la génération de graphes et à identifier les opportunités de recherche ouvertes dans le domaine de la génération de graphes profonds. Au meilleur de nos connaissances, il s'agit de la première revue complète des modèles génératifs profonds pour la génération de graphiques. Ci-dessous, nous résumons les principales contributions de cette revue :

Cet article propose une taxonomie de modèles génératifs profonds pour la génération de graphes, classés par problématique et approche. Les avantages, les inconvénients et les relations entre les différentes sous-catégories sont présentés. Des modèles génératifs profonds pour la génération de graphiques et des modèles génératifs profonds de base sont décrits, analysés et comparés en détail.

• Nous résumons et classifions les procédures et métriques d'évaluation existantes, les résultats sur les ensembles de données de référence et les modèles génératifs profonds correspondants pour les tâches de génération de graphiques.
• Nous présentons les domaines d'application existants des modèles génératifs de profondeur de graphe, ainsi que les avantages et opportunités potentiels qu'ils apportent à ces applications.
• Nous présentons plusieurs questions ouvertes et des orientations de recherche futures prometteuses dans le domaine des modèles génératifs profonds pour la génération de graphes.

Modèle générateur de profondeur inconditionnel pour la génération de graphiques

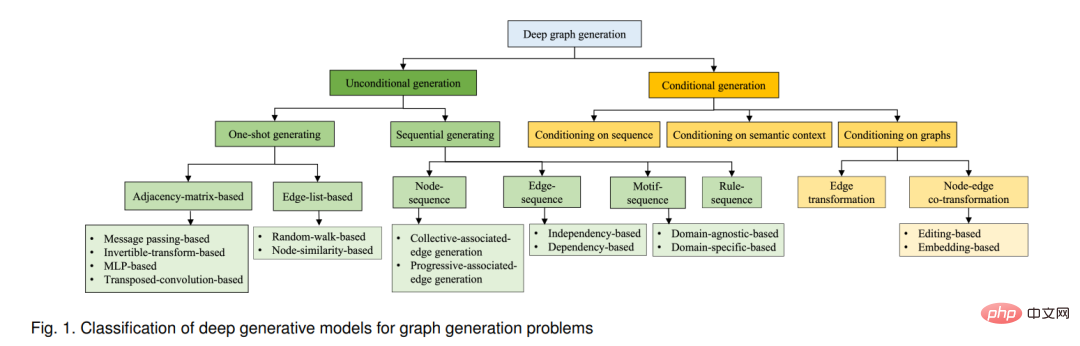
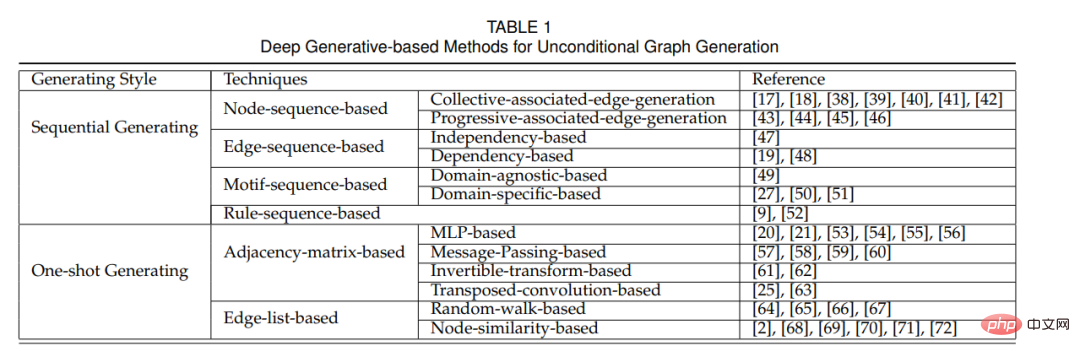
Le but de la génération inconditionnelle de cartes de profondeur est d'échantillonner un ensemble de graphiques réels observés à partir de la distribution réelle p(G) via un modèle générateur de profondeur. Apprenez le modèle p de distribution (G). Selon le style du processus de génération, nous pouvons diviser ces méthodes en deux branches principales : (1) Génération séquentielle : générer des nœuds et des arêtes en séquence (2) Génération unique : construire un modèle de graphe probabiliste selon la représentation matricielle ; et générer en même temps des nœuds et des arêtes. Les deux méthodes de génération de graphiques présentent des avantages et des inconvénients. La génération séquentielle, tout en exécutant efficacement les décisions locales de la génération précédente, a du mal à maintenir des dépendances à long terme. Par conséquent, certaines propriétés globales des graphiques (telles que les propriétés sans échelle) sont difficiles à inclure. De plus, les travaux existants sur la génération de séquences se limitent à l'ordonnancement de séquences prédéfinies, laissant le rôle des permutations. Les méthodes de génération ponctuelle peuvent générer et affiner simultanément l'ensemble du graphe (c'est-à-dire les nœuds et les arêtes) à travers plusieurs itérations, modélisant ainsi les propriétés globales du graphe, mais prennent du temps en raison de la nécessité de modéliser collectivement les relations globales entre les nœuds. La complexité dépasse généralement O(N2), ce qui rend la plupart des méthodes difficiles à adapter à de grands graphiques.

Modèle génératif de profondeur conditionnelle pour la génération de graphiques

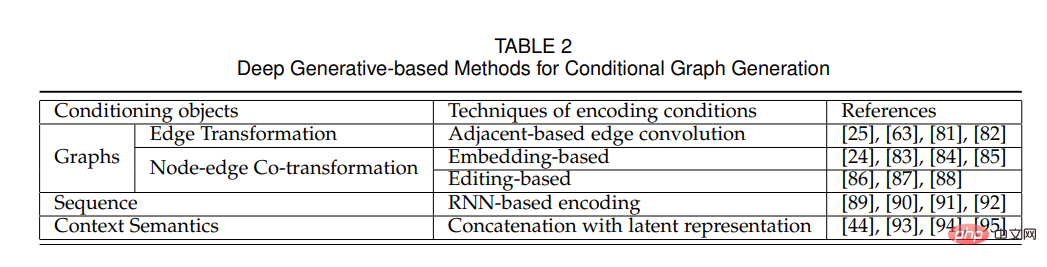
L'objectif de la génération de graphiques de profondeur conditionnelle est d'apprendre le modèle de distribution conditionnelle (G|y). Les informations auxiliaires peuvent être des étiquettes de catégorie, un contexte sémantique, des graphiques provenant d'autres espaces de distribution, etc. Par rapport à la génération inconditionnelle de cartes de profondeur, outre les défis liés à la génération de cartes, la génération conditionnelle doit également prendre en compte la manière d'extraire les caractéristiques de conditions données et de les intégrer dans la génération de cartes.

Par conséquent, afin d'introduire systématiquement les modèles de génération de cartes de profondeur conditionnelles existants, nous décrivons principalement comment ces méthodes gèrent les conditions. Étant donné que les conditions peuvent être n'importe quelle forme d'information auxiliaire, elles sont divisées en trois types, à savoir le graphique, la séquence et le contexte sémantique, comme le montre la partie jaune de l'arbre taxonomique de la figure 1

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!