Une nouvelle recherche de Stanford et de Berkeley renverse la « suprématie quantique » de Google ! Beau en théorie, mais inutile en pratique

Suprématie quantique, ce terme existe depuis près de 4 ans.

En 2019, les physiciens de Google ont annoncé avoir réussi à atteindre l'hégémonie quantique avec une machine de 53 qubits, ce qui constituait une étape symbolique importante.

Dans un article publié dans Nature, il a été déclaré que le système quantique ne prenait que 200 secondes pour effectuer un calcul, alors que le même calcul prenait environ 10 000 ans à l'aide de Summit, le supercalculateur le plus puissant de l'époque.

Qu'est-ce que la suprématie quantique ?

La soi-disant « suprématie quantique » ou « avantage quantique » (ci-après dénommé « suprématie quantique ») signifie que les tâches que les ordinateurs quantiques peuvent accomplir dépassent la portée de tout algorithme classique réalisable.

Même si ces tâches sont confiées aux supercalculateurs traditionnels les plus avancés, le long temps de calcul (souvent des milliers d'années) fera perdre à l'algorithme sa signification pratique.

Fait intéressant, dans les résultats de Google en 2019, il indiquait seulement que l’hégémonie quantique avait été atteinte, mais n’expliquait pas les cas spécifiques dans lesquels les ordinateurs quantiques ont surpassé les ordinateurs classiques.

C'est une question difficile à répondre car actuellement les ordinateurs quantiques sont en proie à des erreurs qui peuvent s'accumuler et nuire aux performances et à la stabilité de l'informatique quantique.

En fait, par rapport au domaine de la réalisation de l'hégémonie quantique, ce que les scientifiques veulent en savoir plus est une autre question : à mesure que les ordinateurs quantiques deviennent de plus en plus grands, les algorithmes classiques peuvent-ils suivre le rythme ?

Scott Aaronson, informaticien à l'Université du Texas à Austin, a déclaré : "Nous espérons qu'à terme, le côté quantique prendra complètement ses distances et mettra complètement fin à cette compétition.

La plupart des chercheurs spéculent que." , La réponse est non.

C'est-à-dire que les algorithmes classiques seront un jour complètement incapables de suivre le rythme de l'informatique quantique, mais ils ont été incapables de le prouver de manière précise et complète. Une façon de prouver définitivement cette inférence est de trouver les conditions dans lesquelles l’informatique quantique peut acquérir un « avantage durable » sur l’informatique traditionnelle.

Maintenant, cette question semble avoir une réponse préliminaire :

Gain de temps : l'informatique quantique produira des erreurs si la correction des erreurs ne peut pas suivre, ces erreurs briseront l'idéal « hégémonie quantique », permettant le classique. algorithmes pour suivre les algorithmes quantiques. ​

Récemment, dans un article préimprimé publié sur Arxiv, une équipe conjointe de l'Université Harvard, de l'Université de Californie à Berkeley et de l'Université hébraïque d'Israël a fait un grand pas en avant pour confirmer cette conclusion.

Ils ont démontré que la correction d'erreurs ciblée est une condition nécessaire pour une suprématie quantique durable dans l'échantillonnage de circuits aléatoires, confirmant les conclusions des recherches de Google il y a quelques années. Au niveau actuel de correction des erreurs quantiques, la suprématie quantique n’existe en réalité pas. ​

Il n'y a plus de « zone dorée » pour la suprématie quantique

Les chercheurs ont développé un algorithme classique capable de simuler des expériences d'échantillonnage de circuits aléatoires lorsque des erreurs existent pour prouver cette conclusion.

Commencez avec un tableau de qubits et manipulez ces qubits de manière aléatoire à l'aide d'opérations appelées « portes quantiques ». Certaines portes quantiques provoquent l’intrication de paires de qubits, ce qui signifie qu’ils partagent un état quantique qui ne peut être décrit individuellement.

La configuration répétée de ces portes quantiques dans des circuits multicouches peut permettre aux qubits d'entrer dans des états intriqués plus complexes.

Pour comprendre cet état quantique, les chercheurs ont mesuré tous les qubits du réseau. Ce comportement provoque l’effondrement de l’état quantique collectif de tous les qubits en une chaîne aléatoire de bits ordinaires, à savoir des 0 et des 1.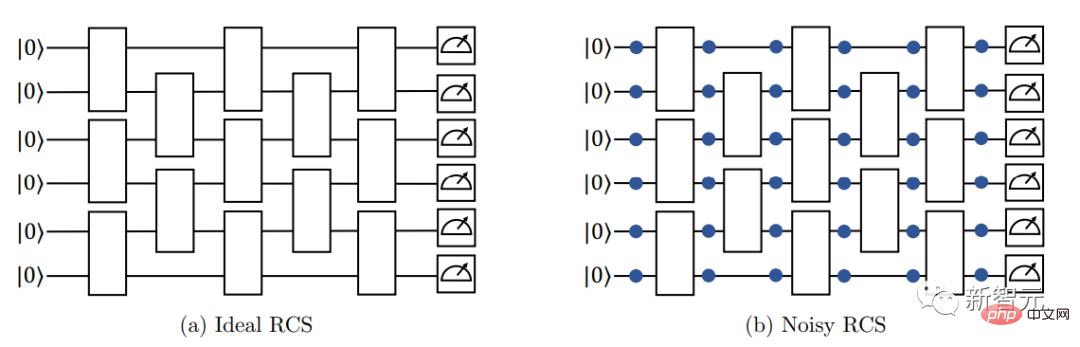

Le nombre de résultats possibles augmente rapidement avec le nombre de qubits dans le tableau. Dans l'expérience de Google de 2019, 53 qubits contenaient près de 10 000 milliards de résultats.

De plus, cette méthode nécessite plusieurs mesures répétées à partir d'un circuit aléatoire pour construire une carte de distribution de probabilité des résultats.

La question concernant la suprématie quantique est la suivante : est-il difficile, voire impossible, d'imiter cette distribution de probabilité avec un algorithme classique qui n'utilise aucune intrication ?

En 2019, des chercheurs de Google ont prouvé que cet objectif est difficile à atteindre pour les circuits quantiques sans erreur qui ne produisent pas d'erreurs. Il est en effet difficile de simuler sans erreurs une expérience d’échantillonnage de circuits aléatoires en utilisant des algorithmes classiques.

Du point de vue de la complexité informatique, lorsque le nombre de qubits augmente, la complexité informatique des algorithmes de classification traditionnels augmente de façon exponentielle, tandis que la complexité informatique des algorithmes quantiques augmente de manière polynomiale.

Lorsque n augmente suffisamment grand, un algorithme exponentiel en n est loin derrière tout algorithme polynomial en n.

C'est la différence à laquelle nous faisons référence lorsque nous parlons d'un problème difficile pour un ordinateur classique mais facile pour un ordinateur quantique. Les meilleurs algorithmes classiques prennent un temps exponentiel, tandis que les ordinateurs quantiques peuvent résoudre des problèmes en temps polynomial.

Cependant, l'article de 2019 n'a pas pris en compte l'impact des erreurs causées par des portes quantiques imparfaites, et la conclusion de la recherche a en fait laissé un trou. En d'autres termes, l'échantillonnage de circuits aléatoires sans correction d'erreur peut-il encore atteindre l'hégémonie quantique ?

En fait, si l'on considère les erreurs qui se produisent dans l'intrication quantique et peuvent s'accumuler, alors la difficulté de simuler des expériences d'échantillonnage de circuits aléatoires avec des algorithmes classiques sera considérablement réduite. Et si la complexité informatique de la simulation d’algorithmes classiques est réduite au même niveau polynomial que celle des algorithmes quantiques, l’hégémonie quantique n’existera plus.

Ce nouvel article montre que, en supposant que la profondeur du circuit reste constante, disons 3 couches très peu profondes, à mesure que le nombre de qubits augmente, il n'y aura pas trop d'intrication quantique et la sortie peut toujours être simulée de manière classique.

D'un autre côté, si la profondeur du circuit est augmentée pour suivre le nombre croissant de qubits, alors l'effet cumulatif des erreurs de porte quantique diluera la complexité causée par l'intrication, et il deviendra encore plus facile de simuler le sortie avec des algorithmes classiques.

Il existe une « zone dorée » entre les deux, c'est-à-dire la fenêtre dans laquelle l'hégémonie quantique peut continuer à survivre, c'est-à-dire la plage où les simulations algorithmiques traditionnelles ne peuvent pas suivre l'intrication quantique.

Avant la publication de cet article, même si le nombre de qubits augmentait, la suprématie quantique existait toujours lorsque le nombre de qubits atteignait une certaine plage intermédiaire.

À cette profondeur de circuit, il est difficile de simuler l'algorithme classique à chaque étape, même si la sortie se dégrade régulièrement en raison d'erreurs de l'algorithme quantique.

Ce nouveau papier élimine presque cette "zone dorée". ​

L'article dérive un algorithme classique pour simuler un échantillonnage de circuit aléatoire et prouve que son temps d'exécution est une

fonction polynomiale

du temps nécessaire pour exécuter l'expérience quantique correspondante, plutôt qu'une fonction exponentielle. Ce résultat établit un lien théorique étroit entre la rapidité de la méthode classique d'échantillonnage de circuits aléatoires et la méthode quantique, c'est-à-dire qu'il déclare que l'hégémonie quantique, qui a été réalisée en théorie, n'existe pratiquement pas.

La raison pour laquelle je dis "presque" est que les hypothèses de base du nouvel algorithme ne sont pas valables pour certains circuits moins profonds, laissant un "petit écart" inconnu.

Cependant, peu de chercheurs espèrent encore atteindre la suprématie quantique dans cette lacune. Même Bill Fefferman, informaticien à l'Université de Chicago et l'un des auteurs de l'article de Google de 2019, a déclaré : « Je pense que les chances sont assez faibles. »

On peut dire que selon les normes strictes de la théorie de la complexité informatique, l'échantillonnage de circuits aléatoires ne produira plus de suprématie quantique.

De plus, face à cette conclusion, tous les chercheurs s'accordent sur l'importance cruciale de la correction des erreurs quantiques pour le succès à long terme de l'informatique quantique. Fefferman a déclaré : "En fin de compte, nous avons découvert que la correction des erreurs quantiques est la solution."

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!