Anatomie de l'algorithme d'arbre de décision

Traducteur | Révisé par Zhao Qingyu

| Sun Shujuan

Avant-propos

Dans l'apprentissage automatique, la classification comporte deux étapes, à savoir l'étape d'apprentissage et l'étape de prédiction. Dans la phase d'apprentissage, un modèle est construit sur la base des données d'entraînement fournies ; dans la phase de prédiction, le modèle est utilisé pour prédire la réponse compte tenu des données. Les arbres de décision sont l’un des algorithmes de classification les plus simples à comprendre et à expliquer.

En machine learning, la classification comporte deux étapes, à savoir l'étape d'apprentissage et l'étape de prédiction. Dans la phase d'apprentissage, un modèle est construit sur la base des données d'entraînement fournies ; dans la phase de prédiction, le modèle est utilisé pour prédire la réponse compte tenu des données. Les arbres de décision sont l’un des algorithmes de classification les plus simples à comprendre et à expliquer.

Algorithme d'arbre de décision

L'algorithme d'arbre de décision est un type d'algorithme d'apprentissage supervisé. Contrairement à d’autres algorithmes d’apprentissage supervisé, l’algorithme d’arbre de décision peut être utilisé pour résoudre à la fois des problèmes de régression et de classification.

Le but de l'utilisation des arbres de décision est de créer un modèle de formation qui prédit la classe ou la valeur d'une variable cible en apprenant des règles de décision simples déduites de données précédentes (données de formation).

Dans les arbres de décision, on part de la racine de l'arbre pour prédire l'étiquette de classe d'un enregistrement. Nous comparons la valeur de l'attribut racine avec l'attribut enregistré, et sur la base de la comparaison, nous suivons la branche correspondant à cette valeur et passons au nœud suivant.

Types d'arbres de décision

En fonction du type de variable cible dont nous disposons, nous pouvons diviser l'arbre en deux types :

1 Arbre de décision à variable catégorielle : Un arbre de décision avec une variable cible catégorielle est appelé une décision à variable catégorielle. arbre.

2. Arbre de décision à variable continue : La variable cible de l'arbre de décision est continue, on l'appelle donc un arbre de décision à variable continue.

Exemple : Supposons que nous ayons un problème pour prédire si un client paiera une prime de renouvellement à une compagnie d'assurance. Le revenu d'un client est ici une variable importante, mais les compagnies d'assurance ne disposent pas de détails sur les revenus de tous les clients. Maintenant que nous savons qu'il s'agit d'une variable importante, nous pouvons alors créer un arbre de décision pour prédire les revenus d'un client en fonction de l'occupation, du produit et de diverses autres variables. Dans ce cas, nous prédisons que la variable cible est continue.

Termes importants liés aux arbres de décision

1. Nœud racine : il représente l'ensemble du membre ou de l'échantillon, qui sera ensuite divisé en deux ou plusieurs ensembles du même type.

2. Fractionnement) : Le processus de division d'un nœud en deux ou plusieurs nœuds enfants.

3. Nœud de décision : lorsqu'un nœud enfant se divise en plusieurs nœuds enfants, il est appelé nœud de décision.

4. Nœud feuille/terminal : Un nœud qui ne peut pas être divisé est appelé nœud feuille ou terminal.

5. Élagage : Le processus dans lequel nous supprimons les nœuds enfants d'un nœud de décision est appelé élagage. La construction peut également être considérée comme le processus inverse de la séparation.

6. Branche/Sous-arbre : Une sous-partie de l’arbre entier est appelée branche ou sous-arbre.

7. Nœud parent et enfant : un nœud qui peut être divisé en nœuds enfants est appelé nœud parent, et un nœud enfant est un nœud enfant du nœud parent.

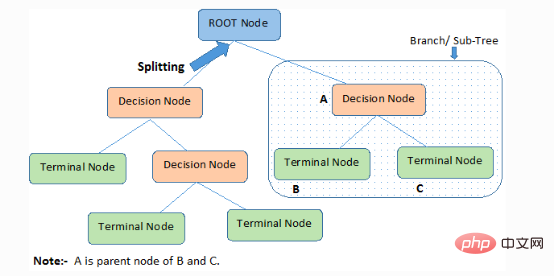
L'arbre de décision classe les échantillons par ordre décroissant de la racine aux nœuds feuilles/terminaux, qui fournissent la méthode de classification de l'échantillon. Chaque nœud de l'arborescence sert de scénario de test pour un certain attribut, et chaque direction descendante à partir du nœud correspond à une réponse possible au scénario de test. Ce processus est de nature récursive et est traité de la même manière pour chaque sous-arbre enraciné sur un nouveau nœud.

Hypothèses faites lors de la création d'arbres de décision

Voici quelques hypothèses que nous faisons lors de l'utilisation des arbres de décision :

●Tout d'abord, prenez l'ensemble de la formation comme racine.

QuantityLes valeurs des caractéristiques sont mieux classées. Si ces valeurs sont continues, elles peuvent être discrétisées avant de construire le modèle.

QuantityLes enregistrements sont distribués de manière récursive en fonction des valeurs d'attribut.

● En utilisant certaines méthodes statistiques pour placer les attributs correspondants au nœud racine de l'arbre ou aux nœuds internes de l'arbre dans l'ordre.

Les arbres de décision suivent la forme d'expression de la somme des produits. La somme des produits (SOP) est également connue sous le nom de forme normale disjonctive. Pour une classe, chaque branche allant de la racine de l'arbre à un nœud feuille de même classe est une conjonction de valeurs, et les différentes branches se terminant dans la classe constituent une disjonction.

Le principal défi dans le processus de mise en œuvre de l'arbre de décision est de déterminer les attributs du nœud racine et de chaque nœud de niveau. Ce problème est le problème de sélection des attributs. Il existe actuellement différentes méthodes de sélection d'attributs pour sélectionner les attributs des nœuds à chaque niveau.

Comment fonctionnent les arbres de décision ?

Les caractéristiques de séparation de la prise de décision affectent sérieusement la précision de l'arbre. Les critères de prise de décision des arbres de classification et des arbres de régression sont différents.

Les arbres de décision utilisent divers algorithmes pour décider de diviser un nœud en deux nœuds enfants ou plus. La création de nœuds enfants augmente l'homogénéité des nœuds enfants. En d’autres termes, la pureté du nœud est augmentée par rapport à la variable cible. L'arbre de décision sépare les nœuds sur toutes les variables disponibles, puis sélectionne les nœuds pouvant produire de nombreux nœuds enfants isomorphes pour le fractionnement.

L'algorithme est sélectionné en fonction du type de variable cible. Examinons ensuite quelques algorithmes utilisés dans les arbres de décision :

ID3→(Extension de D3)

C4.5→(Successeur de ID3)

CART→(Arbre de classification et de régression)

CHAID→ (Chi -la détection automatique des interactions carrées effectue une séparation à plusieurs niveaux lors du calcul des arbres de classification)

MARS → (Multiple Adaptive Regression Splines)

L'algorithme ID3 utilise une approche gourmande descendante Une méthode de recherche qui construit un arbre de décision à travers l'espace des branches possibles sans retour en arrière . Les algorithmes gourmands, comme leur nom l’indique, font toujours ce qui semble être le meilleur choix à un moment donné.

Étapes de l'algorithme ID3 :

1. Il prend l'ensemble d'origine S comme nœud racine.

2. Lors de chaque itération de l'algorithme, parcourez les attributs inutilisés dans l'ensemble S et calculez l'entropie (H) et le gain d'information (IG) de l'attribut.

3. Sélectionnez ensuite l'attribut avec la plus petite entropie ou le plus grand gain d'informations.

4. Séparez ensuite l'ensemble S en utilisant les attributs sélectionnés pour générer des sous-ensembles de données.

5. L'algorithme continue d'itérer sur chaque sous-ensemble, en considérant uniquement les attributs qui n'ont jamais été sélectionnés auparavant à chaque itération.

Méthode de sélection d'attribut

Si l'ensemble de données contient N attributs, alors décider quel attribut placer au nœud racine ou à différents niveaux de l'arborescence en tant que nœud interne est une étape complexe. Le problème ne peut pas être résolu en sélectionnant aléatoirement n’importe quel nœud comme nœud racine. Si nous adoptons une approche aléatoire, nous pourrions obtenir de pires résultats.

Pour résoudre ce problème de sélection d'attributs, les chercheurs ont conçu quelques solutions. Ils suggèrent d'utiliser les critères suivants :

• Entropie
• Gain d'information
• Indice de Gini
• Taux de gain
• Réduction de la variance
• Chi-carré

Calculez la valeur de chaque attribut en utilisant ces critères, puis classez ces valeurs, Et les attributs sont placés dans l'arborescence dans l'ordre, c'est-à-dire que les attributs avec des valeurs élevées sont placés à la position racine.

Lorsque nous utilisons le gain d'information comme critère, nous supposons que les attributs sont catégoriques, tandis que pour l'indice de Gini, nous supposons que les attributs sont continus.

1. Entropie

L'entropie est une mesure du caractère aléatoire des informations traitées. Plus la valeur d’entropie est élevée, plus il est difficile de tirer des conclusions à partir des informations. Lancer une pièce de monnaie est un exemple de comportement qui fournit des informations aléatoires.

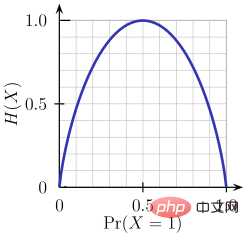
Comme le montre la figure ci-dessus, lorsque la probabilité est de 0 ou 1, l'entropie H(X) est nulle. L'entropie est plus grande lorsque la probabilité est de 0,5 car elle projette un caractère totalement aléatoire dans les données.

La règle suivie par ID3 est la suivante : une branche avec une entropie de 0 est un nœud feuille, et une branche avec une entropie supérieure à 0 doit être davantage séparée.

L'entropie mathématique d'un seul attribut est exprimée comme suit :

où S représente l'état actuel et Pi représente la probabilité d'un événement i dans l'état S ou le pourcentage de classe i dans les nœuds de l'état S.

L'entropie mathématique de plusieurs attributs s'exprime comme suit :

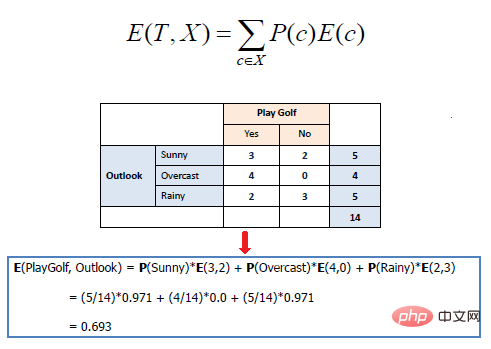
où T représente l'état actuel et Pour mesurer l'effet d'un entraînement séparé pour un attribut donné en fonction de la classe cible. Construire un arbre de décision est le processus de recherche d'un attribut qui renvoie le gain d'informations le plus élevé et l'entropie la plus faible.

L'augmentation de l'information est la diminution de l'entropie. Il calcule la différence d'entropie avant séparation et la différence d'entropie moyenne après séparation de l'ensemble de données en fonction de la valeur d'attribut donnée. L'algorithme d'arbre de décision ID3 utilise la méthode de gain d'informations.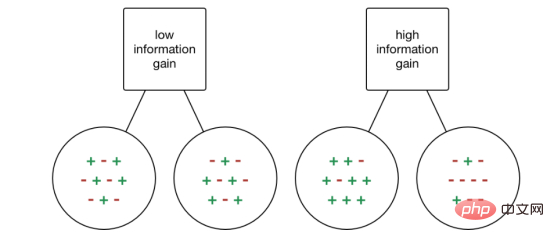

IG s'exprime mathématiquement comme suit :

En utilisant une méthode plus simple, nous pouvons tirer la conclusion suivante :

où avant est l'ensemble des données avant le fractionnement, et K est le résultat du fractionnement Le nombre de sous-ensembles, (j, après) est le sous-ensemble divisé j.

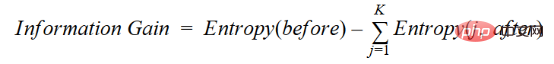3. Indice de Gini

Vous pouvez comprendre l'indice de Gini comme une fonction de coût utilisée pour évaluer la séparation dans un ensemble de données. Il est calculé en soustrayant de 1 la somme des carrés des probabilités pour chaque classe. Il favorise le cas de partitions plus grandes et est plus facile à mettre en œuvre, tandis que le gain d'informations favorise le cas de partitions plus petites avec des valeurs

différentes.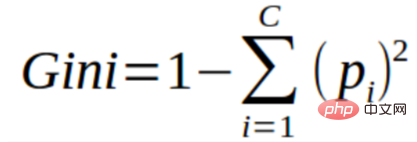

L'indice de Gini est indissociable de la variable cible catégorique « réussite » ou « échec ». Il effectue uniquement une séparation binaire. Plus le coefficient de Gini est élevé, plus le degré d’inégalité est élevé et plus l’hétérogénéité est forte.

Les étapes pour calculer la séparation de l'indice de Gini sont les suivantes :

• Calculez le coefficient de Gini du nœud enfant, en utilisant la formule ci-dessus (p²+q²) pour le succès (p) et l'échec (q).
• Calculez l'indice de coefficient de Gini de la séparation en utilisant le score de Gini pondéré de chaque nœud de la séparation.

CART (Classification and Regression Tree) utilise la méthode d'index de Gini pour créer des points de séparation.

4. Taux de gain

Le gain d'informations a tendance à sélectionner des attributs avec un grand nombre de valeurs comme nœuds racines. Cela signifie qu’il préfère les propriétés comportant un grand nombre de valeurs différentes.

C4.5 est une méthode améliorée d'ID3, qui utilise le rapport de gain, qui est une modification du gain d'information pour réduire son biais, qui est généralement la meilleure méthode de choix. Le taux de gain résout le problème du gain d'information en prenant en compte le nombre de branches avant de procéder au fractionnement. Il corrige le gain d'informations en prenant en compte des informations intrinsèques distinctes.

Supposons que nous ayons un ensemble de données contenant les utilisateurs et leurs préférences en matière de genre de film en fonction de variables telles que le sexe, la tranche d'âge, la classe, etc. Avec l'aide du gain d'informations, vous vous séparerez en « Sexe » (en supposant qu'il ait le gain d'informations le plus élevé), désormais les variables « Groupe d'âge » et « Note » peuvent être tout aussi importantes, avec l'aide du taux de gain, nous pouvons choisir les propriétés qui sont séparés dans la couche suivante.

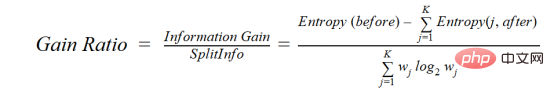
où before est l'ensemble de données avant la séparation, K est le nombre de sous-ensembles générés par la séparation, (j, après) est le sous-ensemble j après la séparation.

5. Réduction de la variance

La réduction de la variance est un algorithme utilisé pour les variables cibles continues (problèmes de régression). L'algorithme utilise la formule de variance standard pour choisir la meilleure séparation. Choisissez la séparation avec la variance la plus faible comme critère de séparation de la population :

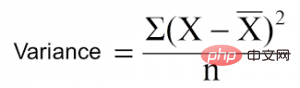
est la moyenne, X est la valeur réelle et n est le nombre de valeurs.

Étapes pour calculer la variance :

• Calculez la variance de chaque nœud.
• Calculez la variance de chaque séparation et utilisez-la comme moyenne pondérée de la variance de chaque nœud.

6. Chi-carré

CHAID est l'abréviation de Chi-carré Automatique Interaction Detector. Il s’agit de l’une des méthodes de classification des arbres les plus anciennes. Trouvez la différence statistiquement significative entre un nœud enfant et son nœud parent. Nous le mesurons par la somme des carrés des différences entre les fréquences observées et attendues de la variable cible.

Il fonctionne avec la variable cible catégorielle "Succès" ou "Échec". Il peut effectuer deux ou plusieurs séparations. Plus la valeur du chi carré est élevée, plus la différence entre le nœud enfant et le nœud parent est statistiquement significative. Il génère un arbre appelé CHAID.

Mathématiquement, le chi carré s'exprime comme suit :

Les étapes pour calculer le chi carré sont les suivantes :

• Calculez le chi carré d'un seul nœud en calculant l'écart de succès et échec
• Calculez le chi carré séparé en utilisant la somme de tous les chi carrés de succès et d'échec de chaque nœud séparé

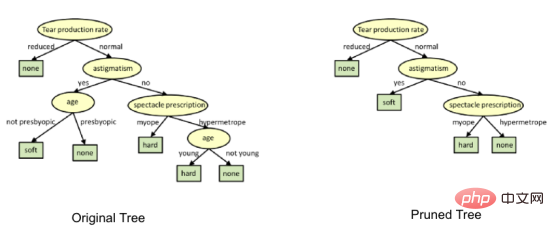
Comment éviter/lutte contre le surajustement des arbres de décision ?

Il existe un un problème courant dans les arbres de décision, en particulier pour un arbre plein de colonnes. Parfois, il semble que l'arbre ait mémorisé l'ensemble de données d'entraînement. Si un arbre de décision n'avait aucune contrainte, il vous donnerait une précision de 100 % sur l'ensemble de données d'entraînement, car dans le pire des cas, il finirait par produire une feuille pour chaque observation. Par conséquent, cela affecte la précision lors de la prédiction d’échantillons qui ne font pas partie de l’ensemble d’apprentissage.

Ici, je présente deux méthodes pour éliminer le surajustement, à savoir l'élagage des arbres de décision et des forêts aléatoires.

1. Taille de l'arbre de décision

Le processus de séparation produira un arbre complètement développé jusqu'à ce que le critère d'arrêt soit atteint. Cependant, les arbres matures sont susceptibles de surajuster les données, ce qui entraîne une mauvaise précision des données invisibles.

Lors de l'élagage, vous taillez les branches de l'arbre, c'est-à-dire supprimez les nœuds de décision à partir des nœuds feuilles afin que la précision globale ne soit pas perturbée. Cela se fait en divisant l'ensemble de données de formation réel en deux ensembles : l'ensemble de données d'entraînement D et l'ensemble de données de validation V, en préparant l'arbre de décision avec l'ensemble de données d'entraînement séparé D, puis en continuant à élaguer l'arbre en conséquence pour optimiser l'ensemble de données de validation V. précision.

Dans l'image ci-dessus, l'attribut "Âge" sur le côté gauche de l'arbre a été élagué car il est plus important sur le côté droit de l'arbre, éliminant ainsi le surapprentissage.

2. Random Forest

Random forest est un exemple d'apprentissage d'ensemble (Ensemble Learning). Nous combinons plusieurs algorithmes d'apprentissage automatique pour obtenir de meilleures performances de prédiction. Étant donné que l'ensemble de données d'entraînement est échantillonné de manière aléatoire lors de la construction de l'arborescence et que des sous-ensembles aléatoires de fonctionnalités sont pris en compte lors de la séparation des nœuds, nous appelons cette méthode aléatoire.

Une technique appelée bagging est utilisée pour créer une collection d'arbres où plusieurs ensembles d'apprentissage sont générés par remplacement.

La technologie d'ensachage utilise un échantillonnage aléatoire pour diviser l'ensemble de données en N échantillons. Ensuite, un seul algorithme d’apprentissage est utilisé pour construire le modèle sur tous les échantillons. Les prédictions sont ensuite combinées par vote parallèle ou calcul de moyenne.

Quel est le meilleur, un modèle linéaire ou un modèle arborescent ?

La question dépend du type de problème que vous essayez de résoudre.

1. Si la relation entre la variable dépendante et la variable indépendante peut être bien modélisée par un modèle linéaire, la régression linéaire sera meilleure que le modèle arborescent.

2. S'il existe une relation hautement non linéaire et complexe entre la variable dépendante et la variable indépendante, le modèle arborescent sera meilleur que la méthode de régression classique.

3. Si vous avez besoin de créer un modèle facile à comprendre, un modèle d'arbre de décision est toujours meilleur qu'un modèle linéaire. Le modèle d'arbre de décision est plus facile à comprendre que la régression linéaire !

Utilisez Scikit-learn pour la construction du classificateur d'arbre de décision

Les données que j'ai utilisées sont des données liées aux supermarchés téléchargées depuis https://drive.google.com/open?id=1x1KglkvJxNn8C8kzeV96YePFnCUzXhBS. , utilisez d'abord le code suivant pour charger toutes les bibliothèques de base :

import numpy as np
import matplotlib.pyplot as plt 
import pandas as pd

Après cela, nous chargeons l'ensemble de données de la manière suivante. Il comprend 5 attributs, l'identifiant de l'utilisateur, le sexe, l'âge, le salaire estimé et le statut d'achat.

data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()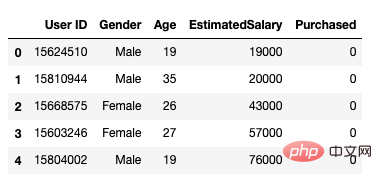

Figure 1 Ensemble de données

Nous incluons uniquement l'âge et le salaire estimé comme variables indépendantes. La capacité d'achat n'a aucun effet et y est la variable dépendante.

feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values
y = data.iloc[:,4].values

L'étape suivante consiste à séparer l'ensemble de données en ensembles de formation et de test.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)

Effectuez ensuite la mise à l'échelle des fonctionnalités

#feature scaling
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)

pour adapter le modèle dans un classificateur d'arbre de décision.

from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier()
classifier = classifier.fit(X_train,y_train)

Faites des prédictions et vérifiez l'exactitude.

#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))

Le classificateur d'arbre de décision a une précision de 91%.

Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)Output:
array([[64,4],
 [ 2, 30]])

Cela signifie qu'il y a 6 observations classées comme erreurs.

Tout d'abord, visualisons les prédictions du modèle

from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()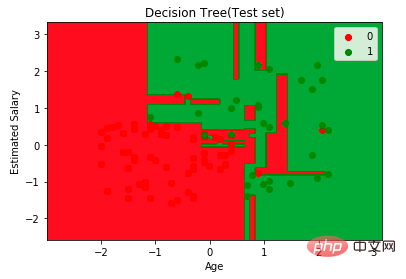

Ensuite, imaginez l'arbre

Ensuite, vous pouvez utiliser la fonction export_graphviz de Scikit-learn pour afficher l'arbre dans un notebook Jupyter. Afin de dessiner l'arbre, nous devons installer Graphviz et pydotplus à l'aide de la commande suivante :

conda install python-graphviz
pip install pydotplus

export_graphviz la fonction convertit le classificateur d'arbre de décision en un fichier de points, pydotplus convertit le fichier de points en png ou en un formulaire affiché sur Jupyter, implémentation spécifique Voici comment procéder :

from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplusdot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

在决策树形图中，每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数，它代表了节点的纯度。当一个节点的所有记录都属于同一个类时，您可以说它是纯节点，这种节点称为叶节点。

在这里，生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中，我会通过修剪的方式来优化树。

随后优化决策树分类器

criteria: 该选项默认配置是Gini，我们可以通过该项选择合适的属性选择方法，该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。

splitter: 该选项默认配置是" best "，我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。

max_depth：默认配置是None，我们可以通过该参数设置树的最大深度。若设置为None，则节点将展开，直到所有叶子包含的样本小于min_samples_split。最大深度值越高，过拟合越严重，反之，过拟合将不严重。

在Scikit-learn中，只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。

# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

至此分类率提高到94%，相对之前的模型来说，其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。

dot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,
filled=True, rounded=True,
special_characters=True, feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

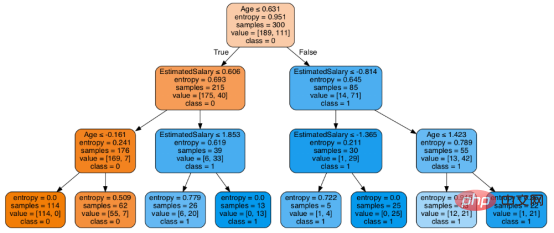
上图是经过修剪后的模型，相对之前的决策树模型图来说，其更简单、更容易解释和理解。

总结

在本文中，我们讨论了很多关于决策树的细节，它的工作方式，属性选择措施，如信息增益，增益比和基尼指数，决策树模型的建立，可视化，并使用Python Scikit-learn包评估和优化决策树性能，这就是这篇文章的全部内容，希望你们能喜欢它。

译者介绍

赵青窕，51CTO社区编辑，从事多年驱动开发。

原文标题：​​Decision Tree Algorithm, Explained​​，作者：Nagesh Singh Chauhan

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!