
Bonjour à tous, je m'appelle Peter~
Les informations sur les différents algorithmes de réduction de dimensionnalité sur Internet sont mitigées et la plupart d'entre eux ne fournissent pas de code source. Voici un projet GitHub qui utilise Python pour implémenter 11 algorithmes classiques d'extraction de données (réduction de la dimensionnalité des données), notamment : PCA, LDA, MDS, LLE, TSNE, etc., avec des informations et des effets d'affichage pertinents très adaptés aux débutants et aux apprenants automatiques ; ceux qui viennent de commencer le data mining.
La réduction dite de dimensionnalité consiste à utiliser un ensemble de vecteurs Zi avec un nombre d pour représenter les informations utiles contenues dans un vecteur Xi avec un nombre D, où d
Habituellement, nous trouverons que les dimensions de la plupart des ensembles de données seront des centaines, voire des milliers, et les dimensions du MNIST classique sont toutes de 64.

Ensemble de données de chiffres manuscrits MNIST
Mais dans les applications réelles, les informations utiles que nous utilisons ne nécessitent pas une dimension aussi élevée, et le nombre d'échantillons requis augmente de façon exponentielle avec chaque dimension supplémentaire. Cela peut directement entraîner un énorme ". désastre de la dimensionnalité" ; la réduction de la dimensionnalité des données peut permettre :
Supprimer le bruit Une fois que nous pouvons traiter correctement ces informations et effectuer la réduction de dimensionnalité correctement et efficacement, cela contribuera grandement à réduire la quantité de calcul et améliorera ainsi l'efficacité du fonctionnement de la machine. La réduction de la dimensionnalité des données est également souvent utilisée dans des domaines tels que le traitement de texte, la reconnaissance faciale, la reconnaissance d'images et le traitement du langage naturel.
Les données dans un espace de grande dimension sont souvent peu distribuées, donc pendant le processus de réduction de dimensionnalité, nous effectuons généralement une suppression de données, qui inclut des données redondantes et des informations invalides, du contenu d'expression répétée, etc.
Par exemple : il y a une image 1024*1024. À l'exception de la zone 50*50 au centre, toutes les autres positions ont des valeurs nulles. Ces informations nulles peuvent être classées comme informations inutiles pour les graphiques symétriques ; partie Il peut être classé comme information en double.
Par conséquent, la plupart des techniques classiques de réduction de dimensionnalité sont également développées sur la base de ce contenu. Les méthodes de réduction de dimensionnalité sont divisées en réductions de dimensionnalité linéaire et non linéaire, et la réduction de dimensionnalité non linéaire est divisée en méthodes basées sur les fonctions du noyau et basées sur les valeurs propres.
Méthodes de réduction de dimensionnalité non linéaire basées sur les fonctions du noyau - KPCA, KICA, KDA
Dimensionnalité non linéaire méthode de réduction (apprentissage de flux) basée sur les valeurs propres - ISOMAP, LLE, LE, LPP, LTSA, MVU
Heucoder, étudiant à la maîtrise en technologie informatique au Harbin Institute of Technology, a compilé PCA, KPCA, LDA, MDS, ISOMAP , LLE, TSNE, AutoEncoder, FastICA, SVD, LE et LPP, un total de 12 algorithmes classiques de réduction de dimensionnalité, et fournissent des informations, des codes et des affichages pertinents. Ce qui suit utilisera principalement l'algorithme PCA comme exemple pour présenter les spécificités. opérations de l'algorithme de réduction de dimensionnalité.
PCA est une méthode de cartographie basée sur la cartographie de l'espace de grande dimension à l'espace de faible dimension. C'est également l'algorithme de réduction de dimensionnalité non supervisé le plus basique. direction du plus grand changement dans les données Projection, ou projection dans la direction qui minimise l’erreur de reconstruction. Elle a été proposée par Karl Pearson en 1901 et constitue une méthode de réduction de dimensionnalité linéaire. Les principes associés à l'ACP sont souvent appelés théorie de la variance maximale ou théorie de l'erreur minimale. Les deux ont le même objectif, mais le processus est différent.
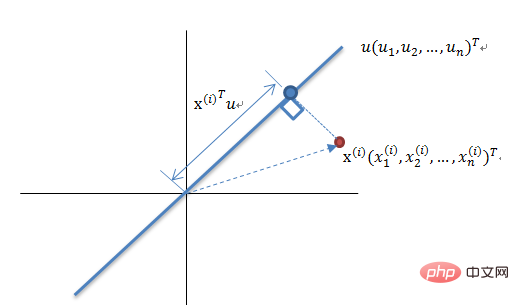
Principe de réduction de dimensionnalité de la théorie de la variance maximale
Réduire un ensemble de vecteurs à N dimensions à K-dimensions (K supérieur à 0, inférieur à N). L'objectif est de sélectionner K bases orthogonales unitaires, et chaque champ est). COV( X,Y) vaut 0, tandis que la variance du champ est aussi grande que possible. Par conséquent, la variance maximale signifie que la variance des données de projection est maximisée. Dans ce processus, nous devons trouver le meilleur espace de projection Wnxk, la matrice de covariance, etc. de l'ensemble de données Xmxn. Le processus d'algorithme est :
L'erreur minimale est la projection linéaire qui minimise le coût moyen de projection. Dans ce processus, nous devons trouver des paramètres tels que la fonction d'évaluation de l'erreur quadratique J0(x0).
Le code de l'algorithme PCA est le suivant :
from __future__ import print_function
from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.cm as cmx
import matplotlib.colors as colors
import numpy as np
%matplotlib inline
def shuffle_data(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
# 正规化数据集 X
def normalize(X, axis=-1, p=2):
lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
lp_norm[lp_norm == 0] = 1
return X / np.expand_dims(lp_norm, axis)
# 标准化数据集 X
def standardize(X):
X_std = np.zeros(X.shape)
mean = X.mean(axis=0)
std = X.std(axis=0)
# 做除法运算时请永远记住分母不能等于 0 的情形
# X_std = (X - X.mean(axis=0)) / X.std(axis=0)
for col in range(np.shape(X)[1]):
if std[col]:
X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
return X_std
# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
if shuffle:
X, y = shuffle_data(X, y, seed)
n_train_samples = int(X.shape[0] * (1-test_size))
x_train, x_test = X[:n_train_samples], X[n_train_samples:]
y_train, y_test = y[:n_train_samples], y[n_train_samples:]
return x_train, x_test, y_train, y_test
# 计算矩阵 X 的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
if not Y.any():
Y = X
n_samples = np.shape(X)[0]
covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
return np.array(covariance_matrix, dtype=float)
# 计算数据集 X 每列的方差
def calculate_variance(X):
n_samples = np.shape(X)[0]
variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
return variance
# 计算数据集 X 每列的标准差
def calculate_std_dev(X):
std_dev = np.sqrt(calculate_variance(X))
return std_dev
# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
# 先计算协方差矩阵
covariance_matrix = calculate_covariance_matrix(X, Y)
# 计算 X, Y 的标准差
std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
return np.array(correlation_matrix, dtype=float)
class PCA():
"""
主成份分析算法 PCA,非监督学习算法.
"""
def __init__(self):
self.eigen_values = None
self.eigen_vectors = None
self.k = 2
def transform(self, X):
"""
将原始数据集 X 通过 PCA 进行降维
"""
covariance = calculate_covariance_matrix(X)
# 求解特征值和特征向量
self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
# 将特征值从大到小进行排序,注意特征向量是按列排的,即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量
idx = self.eigen_values.argsort()[::-1]
eigenvalues = self.eigen_values[idx][:self.k]
eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
# 将原始数据集 X 映射到低维空间
X_transformed = X.dot(eigenvectors)
return X_transformed
def main():
# Load the dataset
data = datasets.load_iris()
X = data.data
y = data.target
# 将数据集 X 映射到低维空间
X_trans = PCA().transform(X)
x1 = X_trans[:, 0]
x2 = X_trans[:, 1]
cmap = plt.get_cmap('viridis')
colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
class_distr = []
# Plot the different class distributions
for i, l in enumerate(np.unique(y)):
_x1 = x1[y == l]
_x2 = x2[y == l]
_y = y[y == l]
class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
# Add a legend
plt.legend(class_distr, y, loc=1)
# Axis labels
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
if __name__ == "__main__":
main()Enfin, nous obtiendrons les résultats de réduction de dimensionnalité comme suit. Parmi eux, si vous obtenez cela lorsque le nombre de fonctionnalités (D) est beaucoup plus grand que le nombre d'échantillons (N), vous pouvez utiliser une petite astuce pour implémenter la conversion de complexité de l'algorithme PCA.
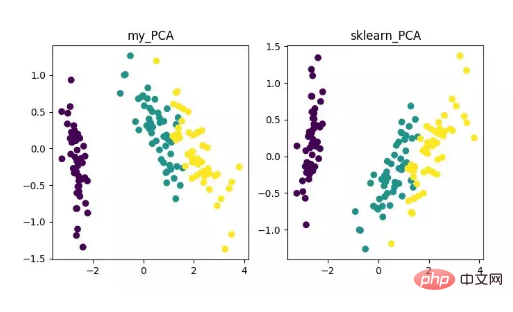
Affichage de l'algorithme de réduction de dimensionnalité PCA
Bien sûr, bien que cet algorithme soit classique et couramment utilisé, ses défauts sont également très évidents. Il peut très bien supprimer la corrélation linéaire, mais face à une corrélation d'ordre élevé, l'effet est faible en même temps, le principe de la mise en œuvre de l'ACP est de supposer que les principales caractéristiques des données sont distribuées dans la direction orthogonale ; pour les directions non orthogonales Il existe plusieurs directions avec de grands écarts et l'effet de l'ACP sera considérablement réduit.
KPCA est le produit de la combinaison de la technologie du noyau et de la PCA. Sa principale différence avec la PCA est que la fonction du noyau est utilisée lors du calcul de la matrice de covariance. , C'est-à-dire après le noyau La matrice de covariance après le mappage des fonctions.
L'introduction de la fonction noyau peut très bien résoudre le problème du mappage de données non linéaires. kPCA peut mapper des données non linéaires sur un espace de grande dimension, où la PCA standard est utilisée pour les mapper sur un autre espace de basse dimension.
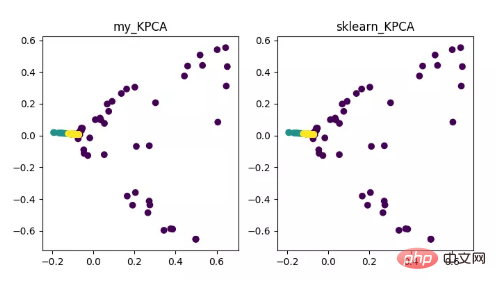
Affichage de l'algorithme de réduction de dimensionnalité KPCA
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/blob/master/codes/PCA/KPCA.py
LDA est une technologie qui peut être utilisée comme extraction de caractéristiques. Son objectif est de projeter dans le sens de maximiser la différence entre les classes et de minimiser la différence au sein de la classe, afin de faciliter des tâches telles que la classification, c'est-à-dire de manière efficace. échantillons séparés de différentes classes. LDA peut améliorer l'efficacité des calculs dans le processus d'analyse des données et réduire le surajustement causé par le désastre de la dimensionnalité pour les modèles qui ne peuvent pas être régularisés.
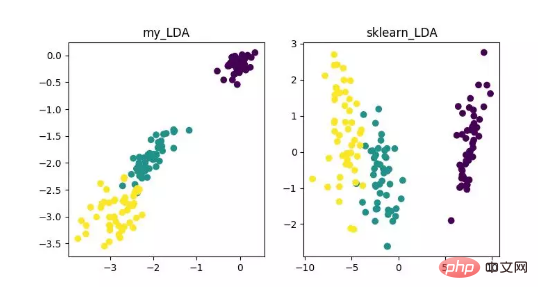
Affichage de l'algorithme de réduction de dimensionnalité LDA
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/LDA
MDS est multidimensionnel L'analyse de mise à l'échelle est une méthode traditionnelle de réduction de dimensionnalité qui représente la perception et les préférences des objets de recherche au moyen de cartes spatiales intuitives. Cette méthode calcule la distance entre deux points d'échantillonnage quelconques afin que la distance relative puisse être maintenue après la projection dans un espace de faible dimension pour réaliser la projection.
Étant donné que MDS dans sklearn adopte une méthode d'optimisation itérative, les méthodes itératives et non itératives sont implémentées ci-dessous.
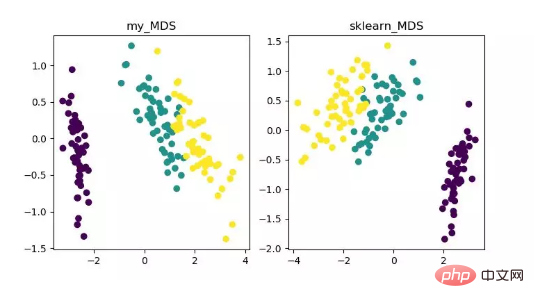
Affichage de l'algorithme de réduction de dimensionnalité MDS
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/MDS
Isomap est l'algorithme de cartographie équimétrique, Cet algorithme peut bien résoudre les lacunes de l'algorithme MDS sur des ensembles de données structurés non linéaires.
L'algorithme MDS maintient la distance entre les échantillons après réduction de dimensionnalité inchangée, tandis que l'algorithme Isomap introduit un graphique de voisinage. Les échantillons sont uniquement connectés à leurs échantillons adjacents, calculent la distance entre les points voisins les plus proches, puis réduisent la distance entre eux sur cette base. . Distance d'entretien.
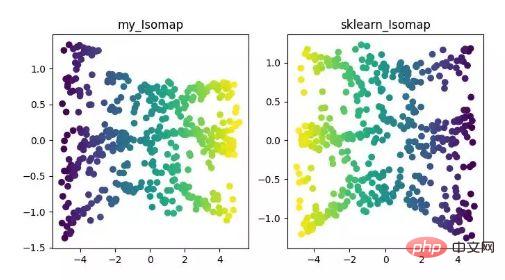
Affichage de l'algorithme de réduction de dimensionnalité ISOMAP
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/ISOMAP
LLE (intégration localement linéaire)LLE est un algorithme d'intégration localement linéaire , qui est un algorithme de réduction de dimensionnalité non linéaire. L'idée centrale de cet algorithme est que chaque point peut être reconstruit approximativement par une combinaison linéaire de plusieurs points adjacents, puis les données de grande dimension sont projetées dans un espace de faible dimension pour maintenir la reconstruction linéaire locale entre les points de données. . relation, c’est-à-dire avoir le même coefficient de reconstruction. Lorsqu'il s'agit de ce que l'on appelle la réduction de dimensionnalité multiple, l'effet est bien meilleur que l'ACP.
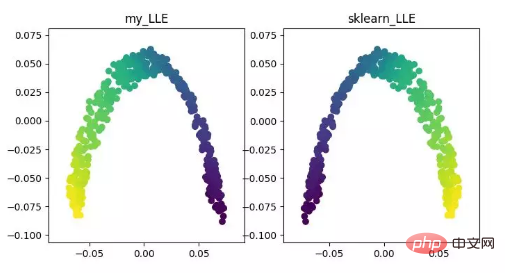
Affichage de l'algorithme de réduction de dimensionnalité LLE
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/LLE
t-SNE est aussi une sorte de non -réduction linéaire L'algorithme dimensionnel est très approprié pour réduire des données de grande dimension à 2 ou 3 dimensions pour la visualisation. Il s'agit d'un algorithme d'apprentissage automatique non supervisé qui reconstruit la tendance des données aux basses latitudes (deux ou trois dimensions) sur la base de la tendance originale des données.
L'affichage des résultats suivant fait référence au code source et peut également être implémenté avec tensorflow (pas besoin de mettre à jour manuellement les paramètres).
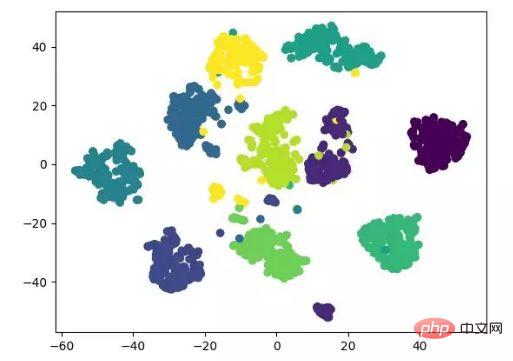
Affichage de l'algorithme de réduction de dimensionnalité t-SNE
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/T-SNE
LE est la carte propre laplacienne, qui est quelque peu similaire à l'algorithme LLE. Elle construit également la relation entre les données d'un point de vue local. Son idée intuitive est d'espérer que les points liés les uns aux autres (points connectés dans le graphique) soient aussi proches que possible dans l'espace dimensionnellement réduit, de cette manière, une solution pouvant refléter la structure géométrique de la variété peut être obtenue ; . Affichage de l'algorithme de réduction de dimensionnalité LE L'idée de l'algorithme de projection à préservation locale est similaire à la carte propre laplacienne. L'idée principale est de construire un mappage de projection en préservant au mieux les informations de structure voisine d'un ensemble de données. Cependant, LPP est différent de LE en obtenant directement la projection. résultat, qui nécessite de résoudre la matrice de projection.
Affichage de l'algorithme de réduction de dimensionnalité LPP
Adresse du code :
https://github.com/heucoder/dimensionnalité_reduction_alo_codes/tree/master/codes/LPP
Heu codeur, est actuellement étudiant en maîtrise en technologie informatique au Harbin Institute of Technology. Il est principalement actif dans le domaine d'Internet. Il est surnommé "Super Love Learning" sur Zhihu. .com/heucoder.
Adresse du projet Github :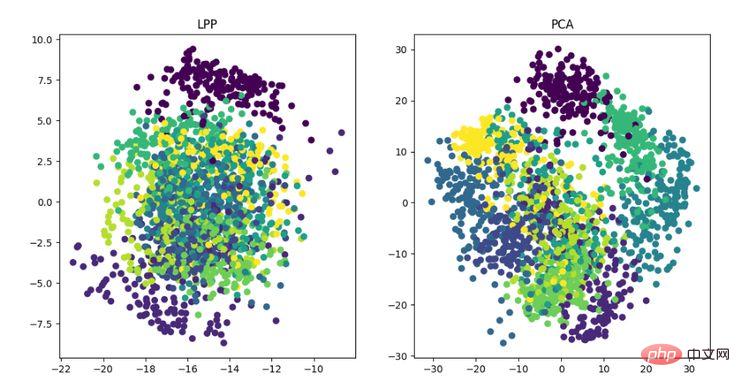
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!