Deep Deterministic Policy Gradient (DDPG) est un algorithme de renforcement profond sans modèle et sans politique inspiré de Deep Q-Network. Il est basé sur Actor-Critic utilisant le gradient de politique. Cet article utilisera pytorch pour le compléter. implémenter et expliquer
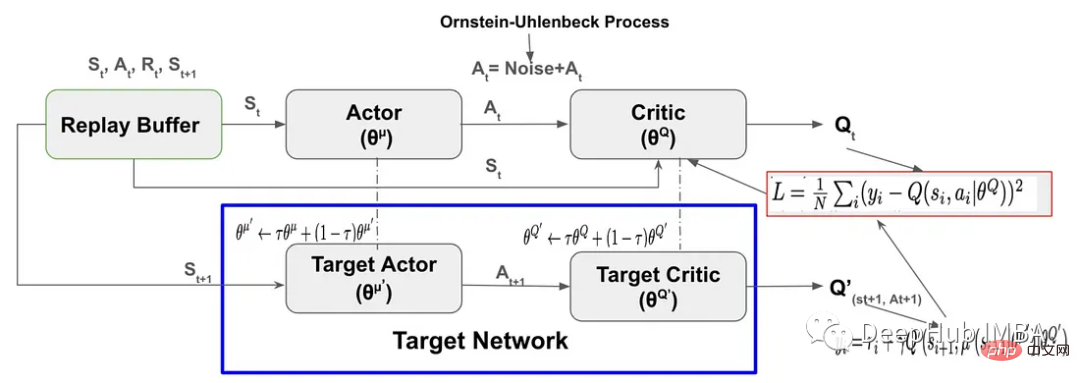
DDPG est
Ensuite, nous avons un Un à mettre en œuvre étape par étape :
DDPG utilise Replay Buffer pour stocker le processus et les récompenses échantillonnées en explorant l'environnement (Sₜ, aₜ, Rₜ, Sₜ+₁). Le Replay Buffer joue un rôle essentiel en aidant l'agent à accélérer l'apprentissage et à assurer la stabilité de DDPG :
class Replay_buffer(): ''' Code based on: https://github.com/openai/baselines/blob/master/baselines/deepq/replay_buffer.py Expects tuples of (state, next_state, action, reward, done) ''' def __init__(self, max_size=capacity): """Create Replay buffer. Parameters ---------- size: int Max number of transitions to store in the buffer. When the buffer overflows the old memories are dropped. """ self.storage = [] self.max_size = max_size self.ptr = 0 def push(self, data): if len(self.storage) == self.max_size: self.storage[int(self.ptr)] = data self.ptr = (self.ptr + 1) % self.max_size else: self.storage.append(data) def sample(self, batch_size): """Sample a batch of experiences. Parameters ---------- batch_size: int How many transitions to sample. Returns ------- state: np.array batch of state or observations action: np.array batch of actions executed given a state reward: np.array rewards received as results of executing action next_state: np.array next state next state or observations seen after executing action done: np.array done[i] = 1 if executing ation[i] resulted in the end of an episode and 0 otherwise. """ ind = np.random.randint(0, len(self.storage), size=batch_size) state, next_state, action, reward, done = [], [], [], [], [] for i in ind: st, n_st, act, rew, dn = self.storage[i] state.append(np.array(st, copy=False)) next_state.append(np.array(n_st, copy=False)) action.append(np.array(act, copy=False)) reward.append(np.array(rew, copy=False)) done.append(np.array(dn, copy=False)) return np.array(state), np.array(next_state), np.array(action), np.array(reward).reshape(-1, 1), np.array(done).reshape(-1, 1)
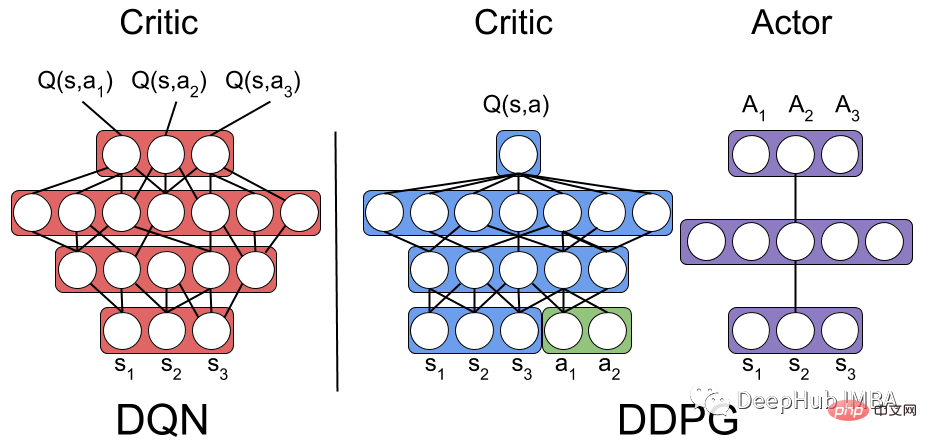
Il s'agit d'une implémentation PyTorch de l'algorithme d'apprentissage par renforcement acteur-critique. Ce code définit deux modèles de réseau neuronal, un acteur et un critique.
L'entrée du modèle Actor : état de l'environnement ; la sortie du modèle Actor : actions à valeurs continues.
L'entrée du modèle Critic : état environnemental et action ; la sortie du modèle Critic : valeur Q, qui est la récompense totale attendue de la paire état-action actuelle.
class Actor(nn.Module): """ The Actor model takes in a state observation as input and outputs an action, which is a continuous value. It consists of four fully connected linear layers with ReLU activation functions and a final output layer selects one single optimized action for the state """ def __init__(self, n_states, action_dim, hidden1): super(Actor, self).__init__() self.net = nn.Sequential( nn.Linear(n_states, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, 1) ) def forward(self, state): return self.net(state) class Critic(nn.Module): """ The Critic model takes in both a state observation and an action as input and outputs a Q-value, which estimates the expected total reward for the current state-action pair. It consists of four linear layers with ReLU activation functions, State and action inputs are concatenated before being fed into the first linear layer. The output layer has a single output, representing the Q-value """ def __init__(self, n_states, action_dim, hidden2): super(Critic, self).__init__() self.net = nn.Sequential( nn.Linear(n_states + action_dim, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, action_dim) ) def forward(self, state, action): return self.net(torch.cat((state, action), 1))
Ajouter du bruit aux actions sélectionnées par un acteur est une technique utilisée dans DDPG pour encourager l'exploration et améliorer le processus d'apprentissage.
Le bruit gaussien ou le bruit Ornstein-Uhlenbeck peuvent être utilisés. Le bruit gaussien est simple et facile à mettre en œuvre, et le bruit d'Ornstein-Uhlenbeck génère un bruit corrélé au temps qui peut aider les agents à explorer plus efficacement l'espace d'action. Mais les fluctuations du bruit Ornstein-Uhlenbeck sont plus douces et moins aléatoires que la méthode du bruit gaussien.
import numpy as np import random import copy class OU_Noise(object): """Ornstein-Uhlenbeck process. code from : https://math.stackexchange.com/questions/1287634/implementing-ornstein-uhlenbeck-in-matlab The OU_Noise class has four attributes size: the size of the noise vector to be generated mu: the mean of the noise, set to 0 by default theta: the rate of mean reversion, controlling how quickly the noise returns to the mean sigma: the volatility of the noise, controlling the magnitude of fluctuations """ def __init__(self, size, seed, mu=0., theta=0.15, sigma=0.2): self.mu = mu * np.ones(size) self.theta = theta self.sigma = sigma self.seed = random.seed(seed) self.reset() def reset(self): """Reset the internal state (= noise) to mean (mu).""" self.state = copy.copy(self.mu) def sample(self): """Update internal state and return it as a noise sample. This method uses the current state of the noise and generates the next sample """ dx = self.theta * (self.mu - self.state) + self.sigma * np.array([np.random.normal() for _ in range(len(self.state))]) self.state += dx return self.state
Pour utiliser le bruit gaussien dans DDPG, vous pouvez ajouter du bruit gaussien directement au processus de sélection d'action de l'agent.
DDPG (Deep Deterministic Policy Gradient) utilise deux ensembles de réseaux neuronaux acteur-critique pour l'approximation des fonctions. Dans DDPG, le réseau cible est Acteur-Critique, qui a la même structure et les mêmes paramétrages que le réseau Acteur-Critique.
Pendant la période de formation, l'agent utilise son réseau Acteur-Critique pour interagir avec l'environnement et stocke les tuples d'expérience (Sₜ, Aₜ, Rₜ, Sₜ+₁) dans le Replay Buffer. L'agent échantillonne ensuite le tampon de relecture et met à jour le réseau acteur-critique avec les données. Plutôt que de mettre à jour les pondérations du réseau cible en les copiant directement à partir du réseau Acteur-Critique, l'algorithme DDPG met lentement à jour les pondérations du réseau cible via un processus appelé mise à jour des cibles logicielles.
La mise à jour de la cible souple est une fraction des poids transférés du réseau Acteur-Critique vers le réseau cible appelée taux de mise à jour cible (τ).
La formule de mise à jour de la cible souple est la suivante :
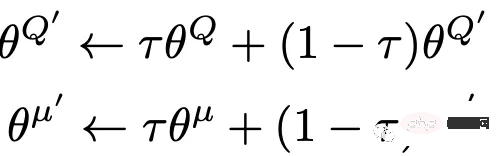
En utilisant la technologie de cible souple, la stabilité de l'apprentissage peut être grandement améliorée.
#Set Hyperparameters # Hyperparameters adapted for performance from capacity=1000000 batch_size=64 update_iteration=200 tau=0.001 # tau for soft updating gamma=0.99 # discount factor directory = './' hidden1=20 # hidden layer for actor hidden2=64. #hiiden laye for critic class DDPG(object): def __init__(self, state_dim, action_dim): """ Initializes the DDPG agent. Takes three arguments: state_dim which is the dimensionality of the state space, action_dim which is the dimensionality of the action space, and max_action which is the maximum value an action can take. Creates a replay buffer, an actor-critic networks and their corresponding target networks. It also initializes the optimizer for both actor and critic networks alog with counters to track the number of training iterations. """ self.replay_buffer = Replay_buffer() self.actor = Actor(state_dim, action_dim, hidden1).to(device) self.actor_target = Actor(state_dim, action_dim,hidden1).to(device) self.actor_target.load_state_dict(self.actor.state_dict()) self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-3) self.critic = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target.load_state_dict(self.critic.state_dict()) self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=2e-2) # learning rate self.num_critic_update_iteration = 0 self.num_actor_update_iteration = 0 self.num_training = 0 def select_action(self, state): """ takes the current state as input and returns an action to take in that state. It uses the actor network to map the state to an action. """ state = torch.FloatTensor(state.reshape(1, -1)).to(device) return self.actor(state).cpu().data.numpy().flatten() def update(self): """ updates the actor and critic networks using a batch of samples from the replay buffer. For each sample in the batch, it computes the target Q value using the target critic network and the target actor network. It then computes the current Q value using the critic network and the action taken by the actor network. It computes the critic loss as the mean squared error between the target Q value and the current Q value, and updates the critic network using gradient descent. It then computes the actor loss as the negative mean Q value using the critic network and the actor network, and updates the actor network using gradient ascent. Finally, it updates the target networks using soft updates, where a small fraction of the actor and critic network weights are transferred to their target counterparts. This process is repeated for a fixed number of iterations. """ for it in range(update_iteration): # For each Sample in replay buffer batch state, next_state, action, reward, done = self.replay_buffer.sample(batch_size) state = torch.FloatTensor(state).to(device) action = torch.FloatTensor(action).to(device) next_state = torch.FloatTensor(next_state).to(device) done = torch.FloatTensor(1-done).to(device) reward = torch.FloatTensor(reward).to(device) # Compute the target Q value target_Q = self.critic_target(next_state, self.actor_target(next_state)) target_Q = reward + (done * gamma * target_Q).detach() # Get current Q estimate current_Q = self.critic(state, action) # Compute critic loss critic_loss = F.mse_loss(current_Q, target_Q) # Optimize the critic self.critic_optimizer.zero_grad() critic_loss.backward() self.critic_optimizer.step() # Compute actor loss as the negative mean Q value using the critic network and the actor network actor_loss = -self.critic(state, self.actor(state)).mean() # Optimize the actor self.actor_optimizer.zero_grad() actor_loss.backward() self.actor_optimizer.step() """ Update the frozen target models using soft updates, where tau,a small fraction of the actor and critic network weights are transferred to their target counterparts. """ for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) self.num_actor_update_iteration += 1 self.num_critic_update_iteration += 1 def save(self): """ Saves the state dictionaries of the actor and critic networks to files """ torch.save(self.actor.state_dict(), directory + 'actor.pth') torch.save(self.critic.state_dict(), directory + 'critic.pth') def load(self): """ Loads the state dictionaries of the actor and critic networks to files """ self.actor.load_state_dict(torch.load(directory + 'actor.pth')) self.critic.load_state_dict(torch.load(directory + 'critic.pth'))
Ici, nous utilisons « MountainCarContinuous-v0 » d'OpenAI Gym pour entraîner notre modèle DDPG RL. L'environnement ici offre une action continue et un espace d'observation, et l'objectif est d'amener la voiture au sommet de la montagne dès que possible. que possible.
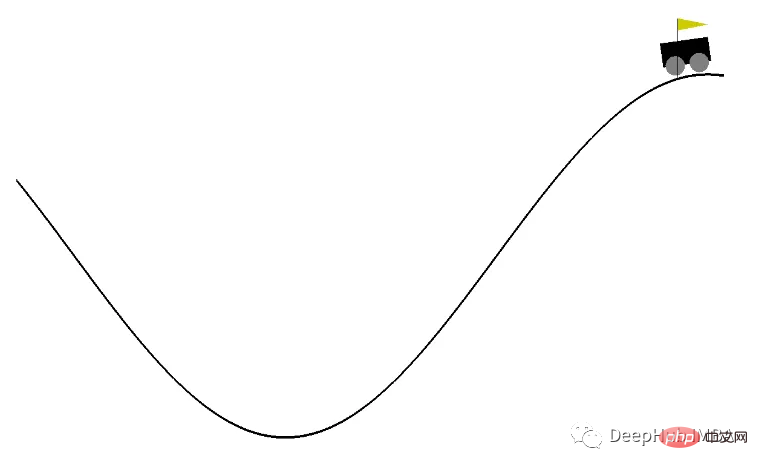
Les différents paramètres de l'algorithme sont définis ci-dessous, comme le nombre maximum de temps d'entraînement, le bruit d'exploration et l'intervalle d'enregistrement, etc. L’utilisation d’une graine aléatoire fixe permet de revenir en arrière sur le processus.
import gym # create the environment env_name='MountainCarContinuous-v0' env = gym.make(env_name) device = 'cuda' if torch.cuda.is_available() else 'cpu' # Define different parameters for training the agent max_episode=100 max_time_steps=5000 ep_r = 0 total_step = 0 score_hist=[] # for rensering the environmnet render=True render_interval=10 # for reproducibility env.seed(0) torch.manual_seed(0) np.random.seed(0) #Environment action ans states state_dim = env.observation_space.shape[0] action_dim = env.action_space.shape[0] max_action = float(env.action_space.high[0]) min_Val = torch.tensor(1e-7).float().to(device) # Exploration Noise exploration_noise=0.1 exploration_noise=0.1 * max_action
Crée une instance de la classe d'agent DDPG pour former l'agent un nombre de fois spécifié. La méthode update() de l'agent est appelée à la fin de chaque tour pour mettre à jour les paramètres, et la méthode save() est utilisée tous les dix tours pour enregistrer les paramètres de l'agent dans un fichier.
# Create a DDPG instance
agent = DDPG(state_dim, action_dim)
# Train the agent for max_episodes
for i in range(max_episode):
total_reward = 0
step =0
state = env.reset()
fort in range(max_time_steps):
action = agent.select_action(state)
# Add Gaussian noise to actions for exploration
action = (action + np.random.normal(0, 1, size=action_dim)).clip(-max_action, max_action)
#action += ou_noise.sample()
next_state, reward, done, info = env.step(action)
total_reward += reward
if render and i >= render_interval : env.render()
agent.replay_buffer.push((state, next_state, action, reward, np.float(done)))
state = next_state
if done:
break
step += 1
score_hist.append(total_reward)
total_step += step+1
print("Episode: t{} Total Reward: t{:0.2f}".format( i, total_reward))
agent.update()
if i % 10 == 0:
agent.save()
env.close()test_iteration=100
for i in range(test_iteration):
state = env.reset()
for t in count():
action = agent.select_action(state)
next_state, reward, done, info = env.step(np.float32(action))
ep_r += reward
print(reward)
env.render()
if done:
print("reward{}".format(reward))
print("Episode t{}, the episode reward is t{:0.2f}".format(i, ep_r))
ep_r = 0
env.render()
break
state = next_stateNous utilisons les paramètres suivants pour faire converger le modèle :
L'effet après un entraînement de 75 tours est le suivant :
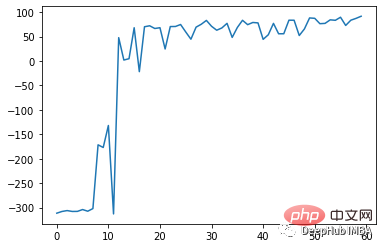
L'algorithme DDPG est une méthode influencé par un algorithme d'acteur-critique hors politique profond sans modèle Q inspiré de l'algorithme de réseau (DQN). Il combine les avantages des méthodes de gradient politique et du Q-learning pour apprendre des politiques déterministes dans des espaces d'action continue.
Semblable à DQN, il utilise un tampon de relecture pour stocker l'expérience passée et le réseau cible pour entraîner le réseau, améliorant ainsi la stabilité du processus de formation.
L'algorithme DDPG nécessite un réglage minutieux des hyperparamètres pour des performances optimales. Les hyperparamètres incluent le taux d'apprentissage, la taille du lot, le taux de mise à jour du réseau cible et les paramètres de bruit de détection. De petits changements dans les hyperparamètres peuvent avoir un impact significatif sur les performances de l'algorithme.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
