
L'algorithme d'augmentation du gradient est l'une des techniques d'apprentissage automatique d'ensemble les plus couramment utilisées. Ce modèle utilise une séquence d'arbres de décision faibles pour construire un apprenant fort. C'est également la base théorique des modèles XGBoost et LightGBM, donc dans cet article, nous allons construire un modèle d'amplification de gradient à partir de zéro et le visualiser.
L'algorithme de boosting de gradient (Gradient Boosting) est un algorithme d'apprentissage d'ensemble qui améliore la précision de prédiction du modèle en construisant plusieurs classificateurs faibles, puis en les combinant en un classificateur fort.
Le principe de l'algorithme de boosting de gradient peut être divisé en les étapes suivantes :
Étant donné que l'algorithme d'augmentation du gradient est un algorithme en série, sa vitesse d'entraînement peut être plus lente. Présentons-le avec un exemple pratique :
Supposons que nous ayons un ensemble de fonctionnalités Xi et une valeur Yi, et que nous souhaitions calculer y Meilleure estimation.
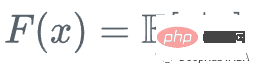
Nous commençons par la moyenne de y
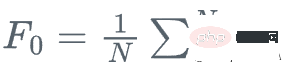
À chaque étape, nous voulons que F_m(x) soit plus proche de y|x.
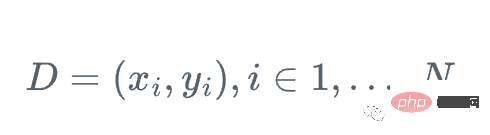
A chaque étape, nous voulons que F_m(x) soit une meilleure approximation de y étant donné x.
D'abord, on définit une fonction de perte
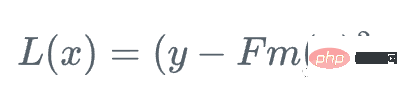
Ensuite, on va dans le sens où la fonction de perte décroît le plus rapidement par rapport à l'apprenant Fm :
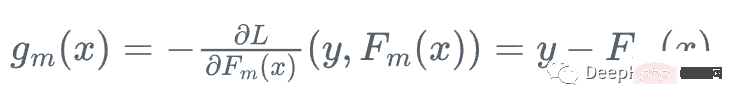
car on ne peut pas calculer y pour chaque x , donc la valeur exacte de ce gradient n'est pas connue, mais pour chaque x_i dans les données d'entraînement, le gradient est exactement égal au résidu de l'étape m : r_i !
Nous pouvons donc utiliser un arbre de régression faible h_m pour approximez la fonction de gradient g_m, pour la formation résiduelle Perform :
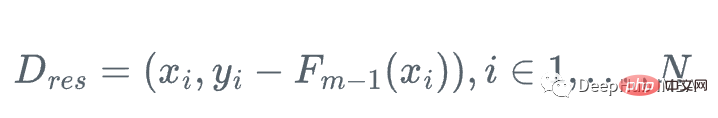
Ensuite, nous mettons à jour l'apprenant
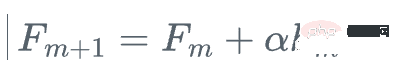
Il s'agit d'une augmentation de gradient au lieu d'utiliser le vrai gradient g_m de la fonction de perte par rapport à. l'apprenant actuel pour mettre à jour l'apprenant actuel F_{m }, utilisez plutôt l'arbre de régression faible h_m pour le mettre à jour.
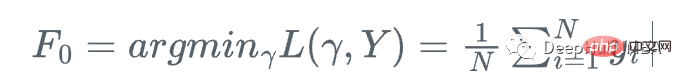
Autrement dit, répétez les étapes suivantes
1. Calculez le résidu :
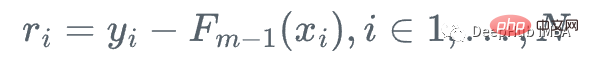
2. Ajustez l'arbre de régression h_m à l'échantillon d'entraînement et à son résidu (x_i, r_i)
3. le modèle de mise à jour alpha par étape
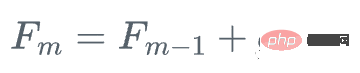
semble compliqué, n'est-ce pas ? Visualisons le processus et il deviendra très clair
Ici, nous utilisons l'ensemble de données lunaires de sklearn, car il s'agit d'un Données catégorielles non linéaires classiques
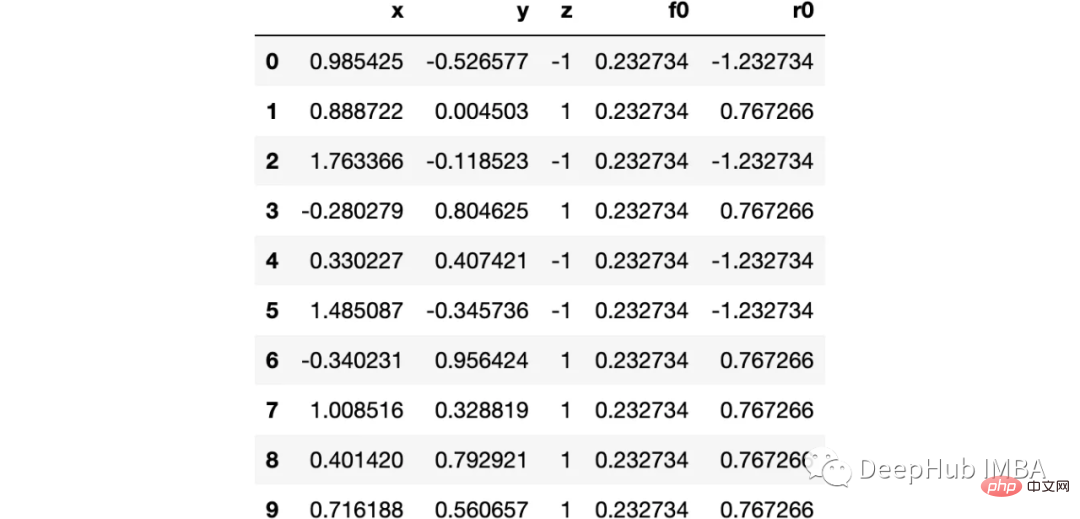
import numpy as np import sklearn.datasets as ds import pandas as pd import matplotlib.pyplot as plt import matplotlib as mpl from sklearn import tree from itertools import product,islice import seaborn as snsmoonDS = ds.make_moons(200, noise = 0.15, random_state=16) moon = moonDS[0] color = -1*(moonDS[1]*2-1) df =pd.DataFrame(moon, columns = ['x','y']) df['z'] = color df['f0'] =df.y.mean() df['r0'] = df['z'] - df['f0'] df.head(10)
Visualisons les données :
下图可以看到,该数据集是可以明显的区分出分类的边界的,但是因为他是非线性的,所以使用线性算法进行分类时会遇到很大的困难。
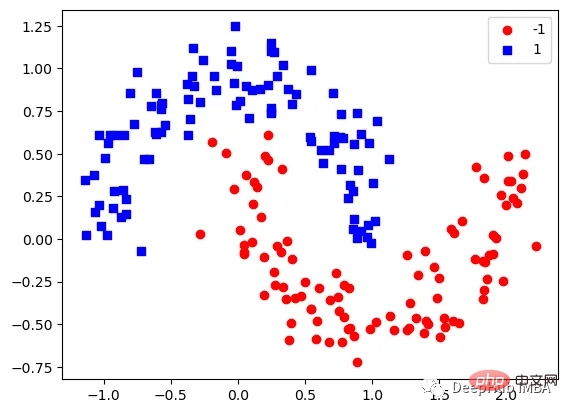
那么我们先编写一个简单的梯度增强模型:
def makeiteration(i:int):
"""Takes the dataframe ith f_i and r_i and approximated r_i from the features, then computes f_i+1 and r_i+1"""
clf = tree.DecisionTreeRegressor(max_depth=1)
clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])
df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)
eta = 0.9
df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']
df[f'r{i}'] = df['z'] - df[f'f{i}']
rmse = (df[f'r{i}']**2).sum()
clfs.append(clf)
rmses.append(rmse)上面代码执行3个简单步骤:
将决策树与残差进行拟合:
clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])
df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)然后,我们将这个近似的梯度与之前的学习器相加:
df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']最后重新计算残差:
df[f'r{i}'] = df['z'] - df[f'f{i}']步骤就是这样简单,下面我们来一步一步执行这个过程。
第1次决策
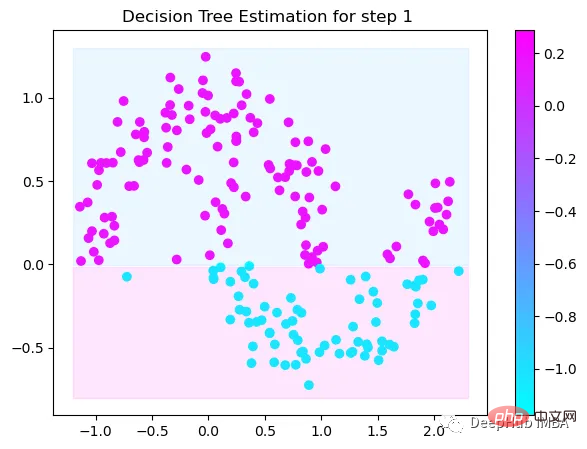
Tree Split for 0 and level 1.563690960407257
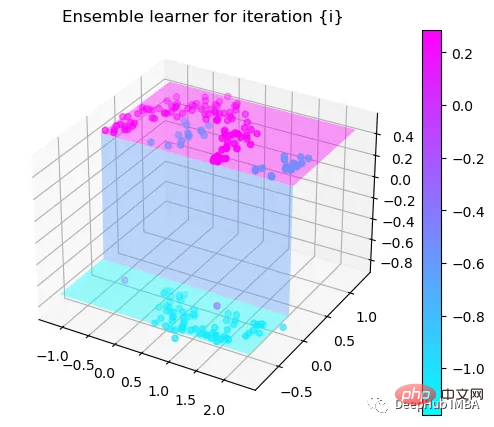
第2次决策
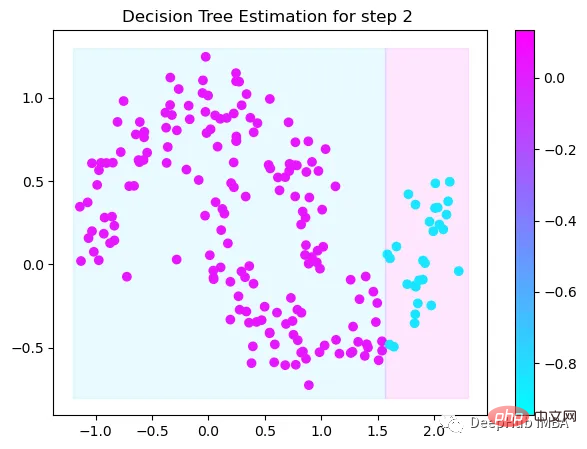
Tree Split for 1 and level 0.5143677890300751
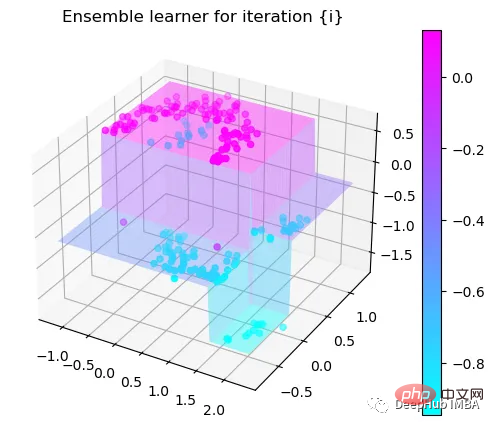
第3次决策
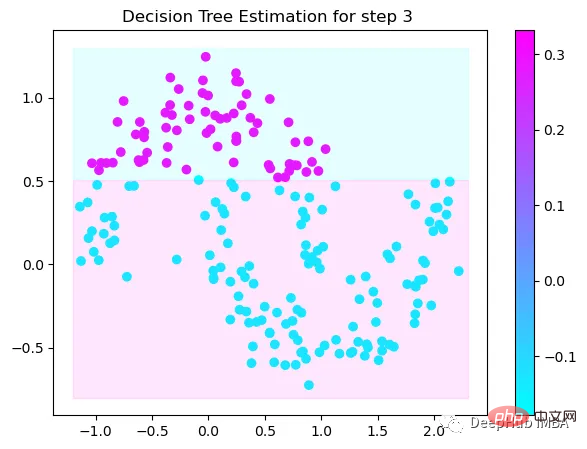
Tree Split for 0 and level -0.6523728966712952
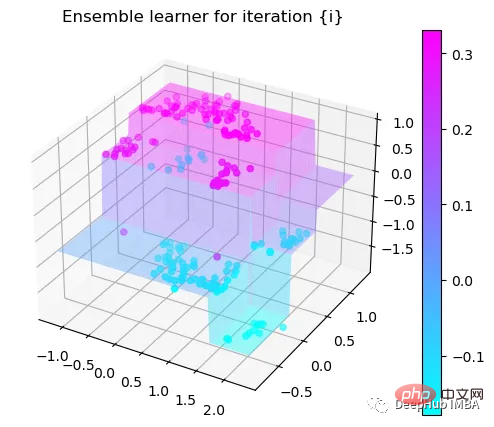
第4次决策
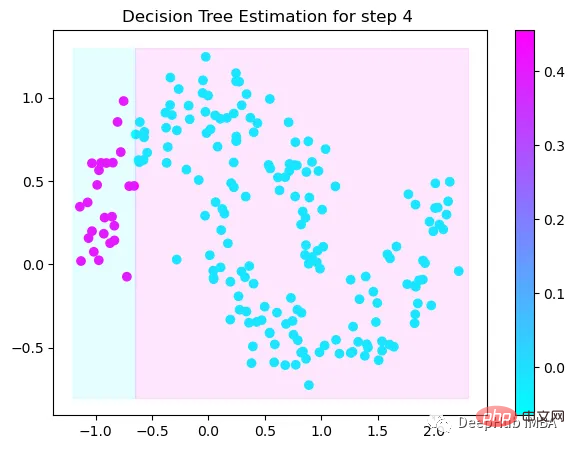
Tree Split for 0 and level 0.3370491564273834
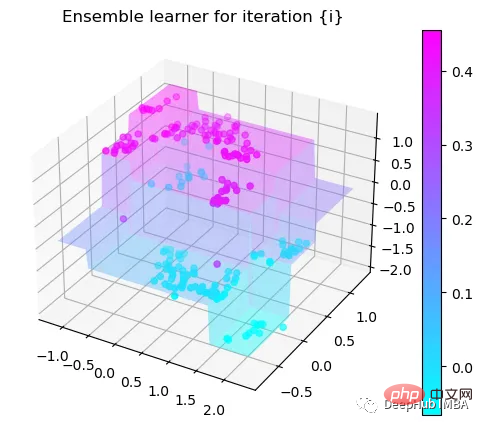
第5次决策
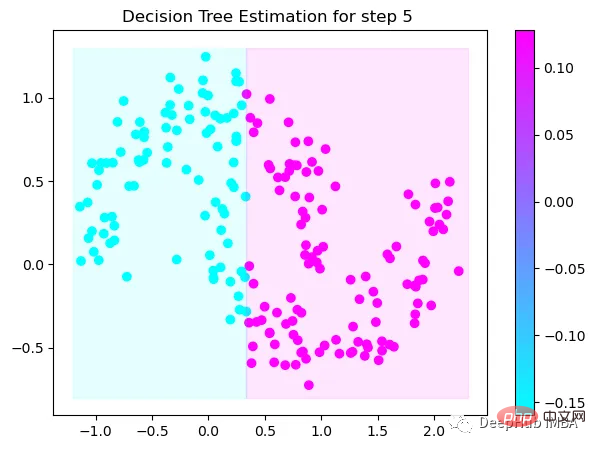
Tree Split for 0 and level 0.3370491564273834
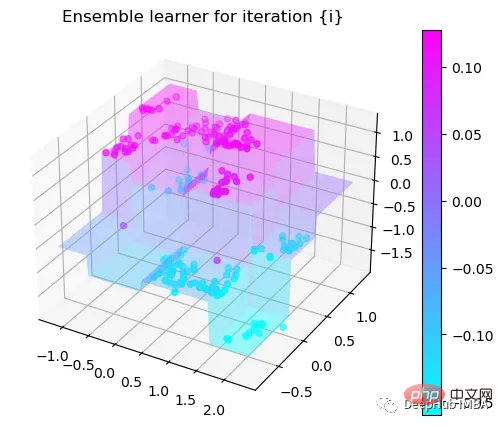
第6次决策
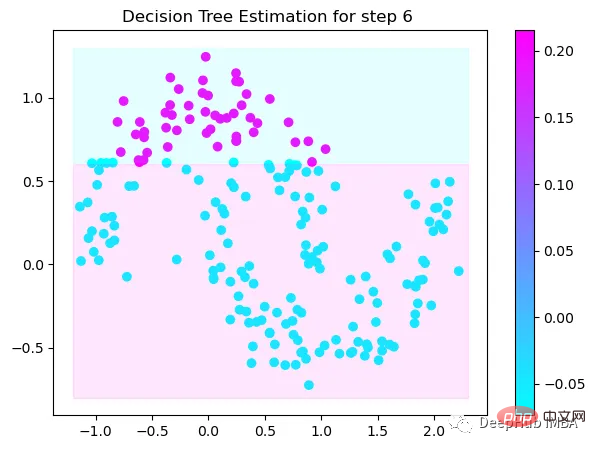
Tree Split for 1 and level 0.022058885544538498
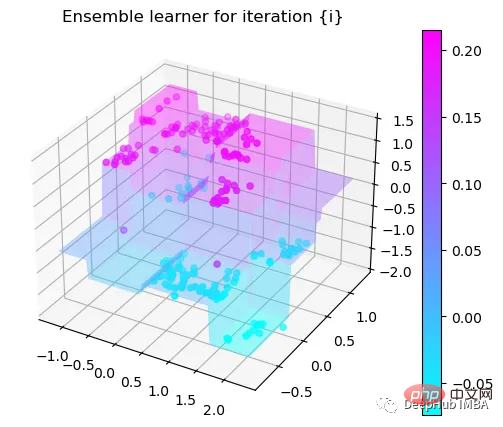
第7次决策
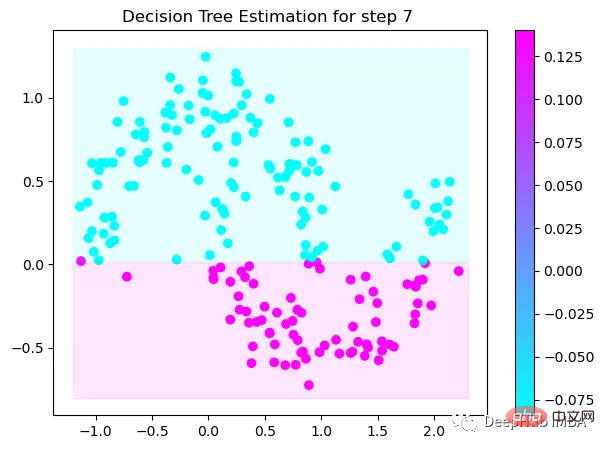
Tree Split for 0 and level -0.3030575215816498
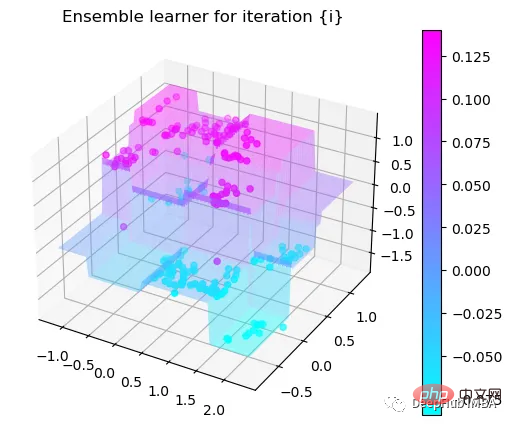
第8次决策
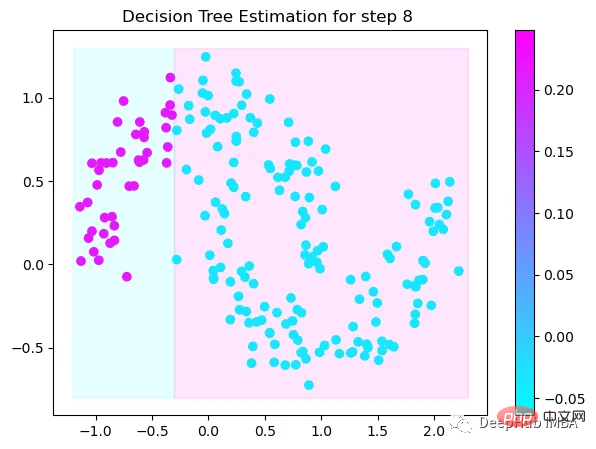
Tree Split for 0 and level 0.6119407713413239
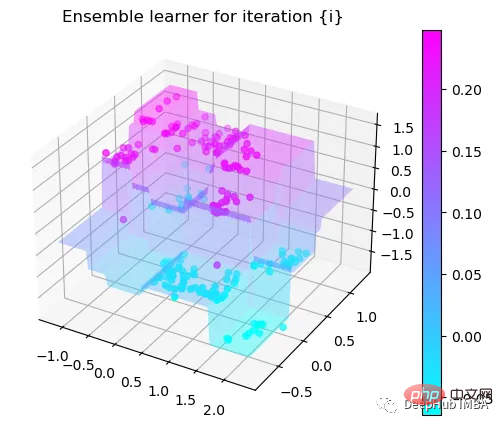
第9次决策
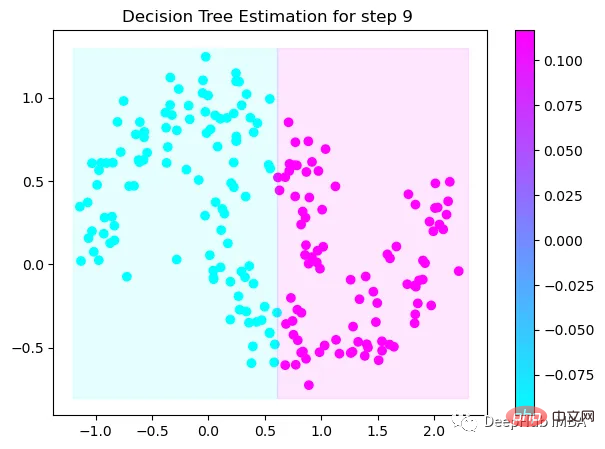
可以看到通过9次的计算,基本上已经把上面的分类进行了区分
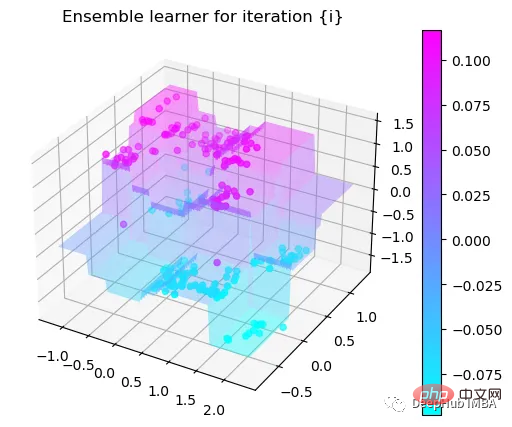
我们这里的学习器都是非常简单的决策树,只沿着一个特征分裂!但整体模型在每次决策后边的越来越复杂,并且整体误差逐渐减小。
plt.plot(rmses)
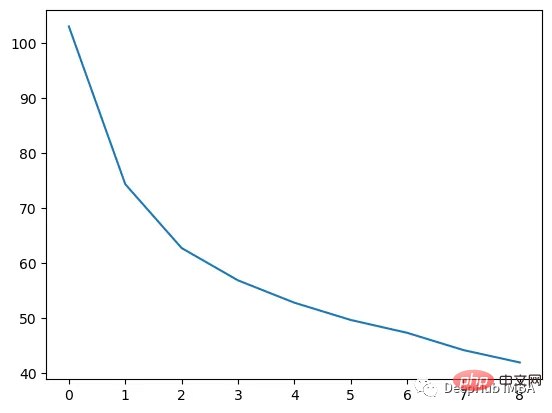
这也就是上图中我们看到的能够正确区分出了大部分的分类
如果你感兴趣可以使用下面代码自行实验:
https://www.php.cn/link/bfc89c3ee67d881255f8b097c4ed2d67
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Utilisation de réécriturecond
Utilisation de réécriturecond
 Windows ne peut pas terminer la solution de formatage du disque dur
Windows ne peut pas terminer la solution de formatage du disque dur
 Quelle est l'inscription dans la blockchain ?
Quelle est l'inscription dans la blockchain ?
 Que signifient les caractères pleine chasse ?
Que signifient les caractères pleine chasse ?
 Diagramme de base de données
Diagramme de base de données
 Comment résoudre l'incompatibilité de charge du serveur
Comment résoudre l'incompatibilité de charge du serveur
 Quels sont les logiciels de dessin ?
Quels sont les logiciels de dessin ?
 Comment obtenir l'adresse de la barre d'adresse
Comment obtenir l'adresse de la barre d'adresse