NP a complètement craqué le mouton et a perdu un mouton ?

Récemment, Yang Liao Ge Yang est devenu populaire partout sur Internet. Il y a eu plus d'articles sur la difficulté du deuxième niveau et comment le réussir. Cependant, il ne devrait y avoir aucun article traitant de la difficulté du jeu du point de vue. de complexité informatique, donc cette fois j'ai également écrit un article sur la complexité informatique pour essayer d'avoir quelques idées.

Le mécanisme du jeu est relativement simple. En termes simples, il existe différents types de blocs sur la carte. Les joueurs peuvent choisir des blocs à placer dans leurs propres emplacements (les emplacements ont une limite supérieure, qui est une constante). la machine à sous est d'éliminer trois blocs du même type. Le but du jeu est d'éliminer tous les blocs. La difficulté du jeu est que les blocs sur la carte sont empilés. Les blocs empilés en dessous ne peuvent pas être sélectionnés (c'est-à-dire déverrouillés) une fois que les blocs au-dessus ont été placés dans les emplacements. Les types sont inconnus car obscurcis.

En fait, le mécanisme de Sheep of Sheep est très similaire à celui de certains mini-jeux, et il a été prouvé que beaucoup de ces mini-jeux sont NP-complets, nous sommes donc relativement confiants dans le fait que nous pouvons également prouver que le Mouton de Mouton promu est NP -complet. Nous donnons ici une structure de réduction relativement faible et simple pour illustrer que le jeu mouton à mouton promu est NP-complet. La généralisation dont nous parlons ici signifie que le nombre de types de blocs n'est pas limité à une constante, le type de bloc bloqué est déterminé et connu, et le nombre de slots est fixé à 3 (une méthode similaire peut être utilisée si le nombre de slots est fixé à 3). Les machines à sous sont d'autres constantes, tant qu'au début du jeu, le joueur est obligé de prendre un type spécial de bloc, qui ne peut être éliminé qu'à la fin de la partie. Pendant tout le processus, ce bloc occupe un emplacement, ce qui équivaut à manquer un emplacement). Bien entendu, nous ne considérons pas ici l’impact des accessoires de jeu.

La réduction de cet article est principalement plagiée à partir de la page Web Computational Complexity of Games and Puzzles qui prouve que le jeu Mah-Jongg (un jeu similaire à Lianliankan, également appelé Mahjong à certains endroits) est NP-complet.

Nous utilisons toujours le problème NP-complet classique de 3-SAT comme problème de réduction. Nous mettons en place 3 piles carrées pour chaque variable dans la formule 3-SAT, une pile carrée est utilisée pour simuler l'affectation de la variable (VRAI ou FAUX), une pile carrée correspond à l'affectation de FAUX, et une pile correspond au affectation de VRAI. La pile de blocs d'affectation pour les variables simulées comporte deux niveaux. Le premier niveau contient 4 blocs identiques correspondant aux variables. Le deuxième niveau contient chacun un bloc avec des variables affectées à VRAI et FAUX et un bloc de remplissage. Le tas de blocs correspondant à la valeur attribuée à FALSE est généralement multicouche (peut également être réduit à une seule couche). La couche supérieure contient deux blocs correspondant à la variable affectée à FALSE (à utiliser avec le tas de blocs précédemment attribué). et la couche inférieure contient les blocs correspondant à la variable affectée aux carrés de clause FALSE (correspondant aux clauses dans lesquelles les variables apparaissent comme non) et aux carrés de remplissage. La structure correspondant au tas de blocs attribué à TRUE est similaire. Enfin, il existe une pile de blocs utilisée pour vérifier la solution. Cette pile est une structure multicouche, le haut contenant des blocs correspondant aux clauses, le milieu étant des blocs correspondant aux variables et le bas étant des blocs correspondant aux clauses.

Nous utilisons un exemple spécifique pour décrire cette réduction, en supposant que l'instance de 3-SAT est 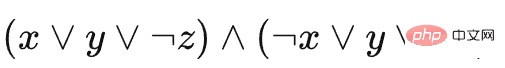. Ensuite l'exemple du jeu de fabrication d'un mouton est le suivant (afin d'exprimer le type et la situation d'empilement de chaque bloc, nous utilisons la vue latérale pour afficher)

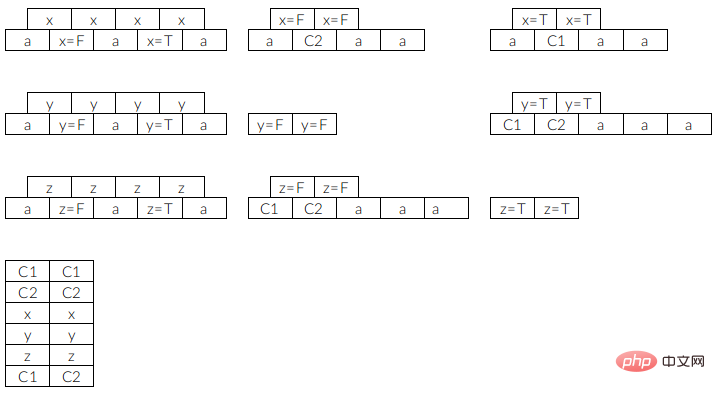
où C1 représente 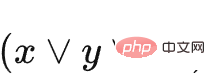et C2 représente 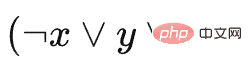, a est un bloc de remplissage, et le bloc a ne supprime aucun bloc, il peut donc être laissé jusqu'à la fin puis tous éliminés sans affecter les autres blocs. Notez que le nombre d'emplacements que nous définissons ici est de 3, ce qui signifie qu'après avoir sélectionné un certain bloc et l'avoir placé dans l'emplacement, vous devez éliminer ce type de bloc, sinon le jeu ne continuera pas.

Si la formule peut être satisfaite, alors les blocs peuvent être éliminés en fonction de l'affectation de chaque variable lorsqu'elle est satisfaite. Par exemple, en supposant que xyz est tous affecté à FALSE, alors nous éliminerons les trois x, y et z les plus à gauche. De cette façon, les carrés de deuxième couche x=F, y=F et z=F seront déverrouillés, et nous pouvons les éliminer. Tous les blocs x=F y=F z=F, alors un bloc C1 et deux blocs C2 seront déverrouillés, puis avec la pile de blocs de vérification inférieure, les deux couches supérieures de la pile de vérification peuvent être éliminées. , puis le bloc xyz variable du milieu sera également déverrouillé. Il peut être éliminé immédiatement, et à la fin il n'y a pas de limite, tous les blocs peuvent être éliminés.

À son tour, si tous les blocs peuvent être éliminés (c'est-à-dire que le niveau peut être passé), alors la formule peut être satisfaite. Notez que si le bloc de variable xyz dans le tas de vérification veut être éliminé, les blocs de clause supérieurs C1 C2 doivent être éliminés en premier, et le bloc de clause est limité au bloc d'affectation, le bloc d'affectation est limité au bloc de variable et le placement du bloc variable La méthode de placement détermine que lors de l'attribution de valeurs aux variables, chaque variable ne peut être attribuée qu'à l'un des FAUX ou VRAI (plus précisément, après avoir arbitrairement éliminé 3 des 4 carrés x au début du jeu, le carrés x=F et x=T (il doit y en avoir un qui n'est pas déverrouillé). Cela signifie que l'ordre dans lequel les blocs sont éliminés implique une affectation qui satisfait la formule.

Cela signifie que la condition nécessaire et suffisante que la formule 3-SAT peut satisfaire est que l'instance de jeu Sheep of Sheep correspondante puisse être passée. Et le mouton appartient clairement à NP, car il peut être déterminé en temps polynomial si une séquence d'opérations peut éliminer tous les blocs, nous avons donc prouvé la proposition suivante :

Proposition : Le type de tous les blocs bloqués est déterminé et Under conditions connues, le gibier de mouton promu est NP-complet.

Pour le dire en termes non humains, vous n'avez aucun moyen de concevoir un algorithme avec une complexité temporelle polynomiale pour déterminer si un niveau mouton à mouton généralisé a une solution, à moins que P = NP (il s'agit d'une équation avec seulement 4 personnages) Vaut un terrain et 1 million de dollars, alors ne restez pas assis à essayer de le prouver ou de le réfuter). Humainement, même si le type de blocage bloqué est certain et connu, l'ordinateur est toujours (presque) incapable de déterminer rapidement si un mouton peut passer le niveau.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!