 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Présenté pour la première fois ! Utiliser l'inférence causale pour effectuer un apprentissage par renforcement partiellement observable
Présenté pour la première fois ! Utiliser l'inférence causale pour effectuer un apprentissage par renforcement partiellement observable
Présenté pour la première fois ! Utiliser l'inférence causale pour effectuer un apprentissage par renforcement partiellement observable
Cet article « Inférence contrefactuelle rapide pour l'apprentissage par renforcement basé sur l'histoire » propose un algorithme d'inférence causale rapide, qui réduit considérablement la complexité informatique de l'inférence causale - à un niveau qui peut être combiné avec l'apprentissage par renforcement en ligne.
La contribution théorique de cet article comporte principalement deux points :
1. Proposition du concept d'effet causal moyenné dans le temps.
2. Extension du fameux critère de porte dérobée de l'estimation univariée de l'effet d'intervention ; L’estimation multivariée de l’effet de l’intervention est appelée critère de porte dérobée.
Contexte
Nécessite la préparation de connaissances de base sur l'apprentissage par renforcement partiellement observable et l'inférence causale. Je n'en présenterai pas trop ici, mais voici quelques portails :
Apprentissage par renforcement partiellement observable :
Explication POMDP https://www.zhihu.com/zvideo/1326278888684187648
Raisonnement causal :
Raisonnement causal dans les réseaux de neurones profonds https://zhuanlan.zhihu.com/p/425331915
Motivation
Extraire/encoder des caractéristiques à partir d'informations historiques est un moyen de base pour résoudre l'apprentissage par renforcement partiellement observable. La méthode courante consiste à utiliser le modèle séquence à séquence (seq2seq) pour coder l'historique. Par exemple, les méthodes d'apprentissage par renforcement LSTM/GRU/NTM/Transformer populaires dans le domaine entrent dans cette catégorie. Le point commun de ce type de méthode est que l’histoire est codée sur la base de la corrélation entre les informations historiques et les signaux d’apprentissage (récompenses environnementales), c’est-à-dire que plus la corrélation d’une information historique est grande, plus le poids attribué est élevé.
Cependant, ces méthodesne peuvent pas éliminer les corrélations confusionnelles causées par l'échantillonnage. Prenons un exemple de récupération d'une clé pour ouvrir la porte, comme le montre la figure ci-dessous :
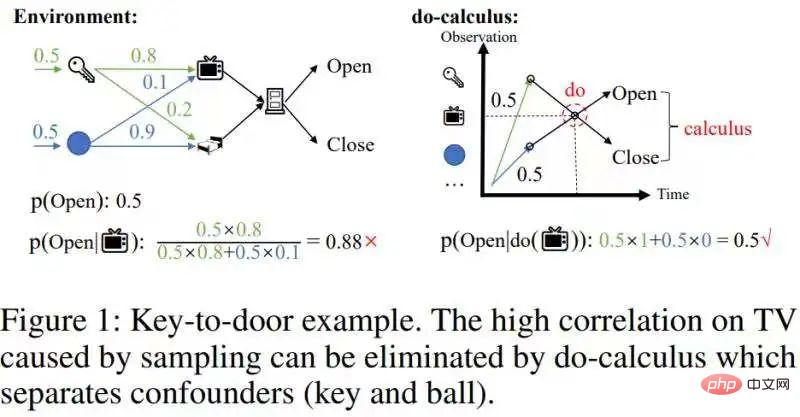
supprimer cette corrélation confusionnelle.
Cette corrélation confusionnelle peut être supprimée par le do-calcul dans l'inférence causale[1] :Séparez les variables de porte dérobée potentiellement déroutantesclé et balle, séparant ainsi la variable de porte dérobée (clé/boule) et TV Corrélation statistique entre les machines , puis intégrer la probabilité conditionnelle de p(Open| , key/ball) par rapport à la variable de porte dérobée (key/ball) (image de droite de la figure 1), et obtenir l'effet réel p(Open |do( ))=0,5. Étant donné que les états historiques ayant des effets causals sont relativement rares, lorsque nous supprimons les corrélations confusionnelles, l’échelle des états historiques peut être considérablement réduite. Par conséquent, nous espérons utiliser l'inférence causale pour supprimer les corrélations confusionnelles dans les échantillons historiques, puis utiliser seq2seq pour coder l'histoire afin d'obtenir une représentation historique plus compacte. (Motivation pour cet article)
[1] Remarque : ce qui est considéré ici est un calcul ajusté à l'aide de la porte dérobée et un lien scientifique populaire https://blog.csdn.net/qq_31063727/article/details /118672598
Difficulté
Réaliser une inférence causale dans des séquences historiques est différent des problèmes généraux d'inférence causale. Les variables de la séquence historique ont à la fois des dimensions temporelles et spatiales , c'est-à-dire une combinaison observation-temps 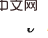 , où o est l'observation et t est l'horodatage (en comparaison, MDP est très convivial et l'état de Markov uniquement a une dimension spatiale). Le chevauchement des deux dimensions rend l'échelle des observations historiques assez grande - en utilisant
, où o est l'observation et t est l'horodatage (en comparaison, MDP est très convivial et l'état de Markov uniquement a une dimension spatiale). Le chevauchement des deux dimensions rend l'échelle des observations historiques assez grande - en utilisant  pour représenter le nombre de valeurs d'observation à chaque horodatage, et en utilisant T pour représenter la durée totale, les valeurs de l'historique state sont
pour représenter le nombre de valeurs d'observation à chaque horodatage, et en utilisant T pour représenter la durée totale, les valeurs de l'historique state sont  espèces (où le corps régulier O( ) est le symbole de complexité). [2]
espèces (où le corps régulier O( ) est le symbole de complexité). [2]
Les méthodes d'inférence causale précédentes sont basées sur la détection d'intervention univariée, qui ne peut traiter qu'une seule variable à la fois. Effectuer un raisonnement causal sur un état historique à grande échelle entraînera une complexité temporelle extrêmement élevée, ce qui rendra difficile la combinaison avec des algorithmes RL en ligne.
[2] Remarque : La définition formelle de l'effet causal d'une intervention univariée est la suivante
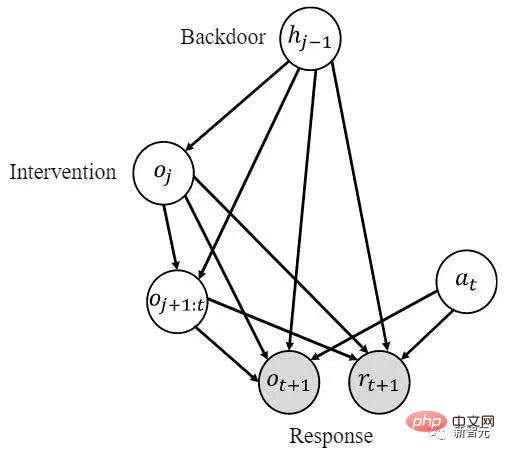
, il est nécessaire d'estimer pour la variable de transfert Pour obtenir l'effet causal de , effectuez les deux étapes suivantes : 1) Intervenir dans l'état historique faites , 2) Utiliser l'état historique précédent comme variable de porte dérobée , comme variable de réponse, et calculez l'intégrale suivante L'effet causal requis

Idée
L'observation (hypothèse) principale de cet article est queles états causals sont rares dans la dimension spatiale. Cette observation est naturelle et courante. Par exemple, lorsque vous ouvrez une porte avec une clé, de nombreux états seront observés au cours du processus, mais la valeur d'observation de la clé détermine si la porte peut être ouverte. proportion de toutes les valeurs d’observation. Profitant de cette rareté, nous pouvons filtrer simultanément un grand nombre d’états historiques sans effets causals grâce à une intervention multivariable. Mais les effets causals ne sont pas rares dans la dimension temporelle C'est aussi une clé pour ouvrir la porte. La clé peut être observée par l'agent la plupart du temps. La densité des effets causals dans la dimension temporelle nous empêche de mener des interventions multivariées : il est impossible de supprimer d’un seul coup un grand nombre d’états historiques sans effets causals.
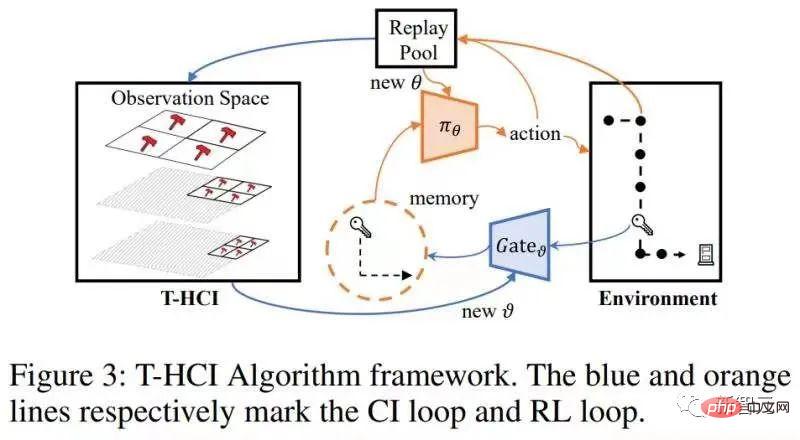
Sur la base des deux observations ci-dessus, notre idée principale est de d'abord faire des inférences dans la dimension spatiale, puis de faire des inférences dans la dimension temporelle. Utiliser la parcimonie dans la dimension spatiale pour réduire considérablement le nombre d'interventions. Afin d'estimer séparément l'effet causal spatial, nous proposons d'obtenir d'abord l'effet causal moyen dans le temps, qui consiste à faire la moyenne des effets causals de plusieurs états historiques au fil du temps (voir le texte original pour les définitions spécifiques). Sur la base de cette idée, nous nous concentrons sur le problème : le problème principal à résoudre est comment calculerl'effet causal conjoint d'une intervention sur plusieurs pas de temps différents Nous améliorons le critère de la porte dérobée et proposons un critère adapté à l'estimation des estimations de l'effet d'une intervention conjointe multivariable. Pour deux variables intervenues critère d'ajustement pas à pas (formule d'ajustement pas à pas) Ce critère sépare les autres variables entre les variables de deux pas de temps adjacents, qui sont appelées variables de porte dérobée pas à pas. Dans un diagramme causal qui satisfait à ce critère, nous pouvons estimer l’effet causal conjoint de deux variables intervenantes. Il comprend deux étapes : étape 1. Utilisez la variable plus petite que i au pas de temps comme variable de porte dérobée pour estimer l'effet causal de do La formule ci-dessus utilise un indicateur variable plus général X. Pour le cas de plus de trois variables, en utilisant continuellement le critère de porte dérobée - en traitant les variables entre les variables intermédiaires adjacentes à chaque pas de temps comme des variables de porte dérobée et en calculant continuellement la formule ci-dessus, nous pouvons obtenir le joint L'effet causal de l'intervention multivariable Théorème 1. Étant donné un ensemble de variables intervenues avec des horodatages différents, si toutes les deux variables temporellement adjacentes répondent à la formule d'ajustement par porte dérobée, alors l'effet causal global peut être estimé avec Spécifiquement pour le problème d'apprentissage par renforcement partiellement observable, après avoir remplacé x dans la formule ci-dessus par l'observation o, il existe la formule de calcul de l'effet causal suivante : Théorème 2. Étant donné À ce stade, l'article donne une formule pour calculer les effets causals spatiaux (c'est-à-dire les effets causals moyennés dans le temps). Cette méthode réduit le nombre d'interventions de O (). Le diagramme de structure de l'algorithme est le suivant L'algorithme contient deux boucles, l'une est la boucle T-HCI et l'autre est la boucle d'apprentissage de la politique. Les deux sont échangées : dans la politique. boucle d'apprentissage, l'agent est échantillonné. Apprenez un certain nombre de tours et stockez les échantillons dans le pool de relecture dans la boucle T-HCI, utilisez les échantillons stockés pour effectuer le processus d'inférence causale mentionné ci-dessus ; Limitations : Le raisonnement causal dans la dimension spatiale a déjà suffisamment compressé l'échelle historique. Bien que l'inférence causale dans la dimension temporelle puisse comprimer davantage l'échelle historique, étant donné que la complexité informatique doit être équilibrée, cet article conserve l'inférence de corrélation dans la dimension temporelle (en utilisant le LSTM de bout en bout sur les états historiques avec des effets causals spatiaux) et n'utilise pas le raisonnement causal. Trois points vérifiés expérimentalement, répondant aux affirmations précédentes : 1) Le T-HCI peut-il améliorer l'efficacité des échantillons des méthodes RL 2) La surcharge de calcul du T-HCI est-elle acceptable en pratique ? -Observations de mines HCI avec effets causals ? Veuillez consulter le chapitre expérimental de l'article pour plus de détails, donc je ne prendrai pas de place ici. Bien entendu, les amis intéressés peuvent également m'envoyer un message/commentaire privé. Orientations pour une expansion future Deux points pour démarrer la discussion : 1. L'HCI ne se limite pas au type d'apprentissage par renforcement. Bien que cet article étudie le RL en ligne, le HCI peut également être naturellement étendu au RL hors ligne, au RL basé sur un modèle, etc., et vous pouvez même envisager d'appliquer le HCI à l'apprentissage par imitation 2. méthode d'attention - les points de séquence avec effet causal reçoivent un poids d'attention 1, sinon ils reçoivent un poids d'attention 0. De ce point de vue, certains problèmes de prédiction de séquence peuvent également tenter d’être traités à l’aide de HCI.  avec la même variable (notée ). En effet, le critère de la porte dérobée ne s'applique pas à l'intervention conjointe de plusieurs variables historiques : Comme le montre la figure ci-dessous, en considérant l'intervention conjointe des variables doubles
avec la même variable (notée ). En effet, le critère de la porte dérobée ne s'applique pas à l'intervention conjointe de plusieurs variables historiques : Comme le montre la figure ci-dessous, en considérant l'intervention conjointe des variables doubles 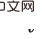 et
et  , vous pouvez voir cette partie de
, vous pouvez voir cette partie de  au pas de temps ultérieur La variable de porte dérobée contient
au pas de temps ultérieur La variable de porte dérobée contient  , et il n'y a pas de variable de porte dérobée commune entre les deux.
, et il n'y a pas de variable de porte dérobée commune entre les deux. 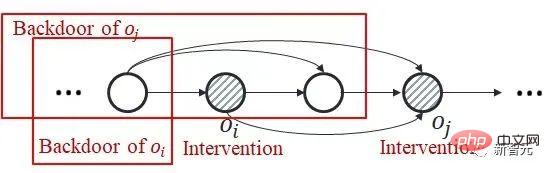
Méthode
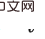 et
et 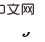 (i
(i
 étape 2. Utilisez la variable de porte dérobée déterminée
étape 2. Utilisez la variable de porte dérobée déterminée  et la déterminée ;
et la déterminée ;  comme conditions, en prenant les variables entre
comme conditions, en prenant les variables entre  et
et 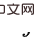 comme nouvelles variables de porte dérobée concernant
comme nouvelles variables de porte dérobée concernant 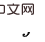 (c'est-à-dire en faisant passer les variables de porte dérobée concernant
(c'est-à-dire en faisant passer les variables de porte dérobée concernant  et
et 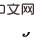 ), estimez la causalité conditionnelle de do
), estimez la causalité conditionnelle de do Effet . L’effet causal conjoint est alors le produit intégral de ces deux parties. Le critère de porte dérobée pas à pas utilise deux étapes du critère de porte dérobée ordinaire, comme le montre la figure ci-dessous
Effet . L’effet causal conjoint est alors le produit intégral de ces deux parties. Le critère de porte dérobée pas à pas utilise deux étapes du critère de porte dérobée ordinaire, comme le montre la figure ci-dessous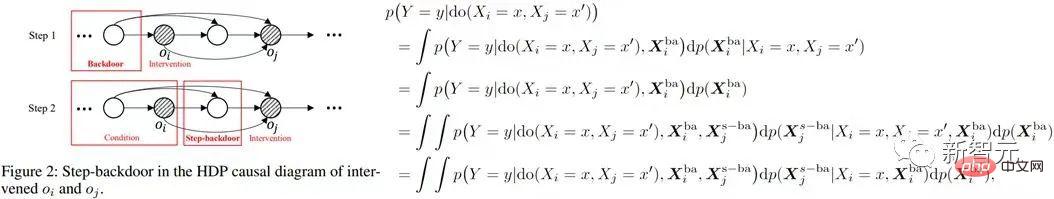
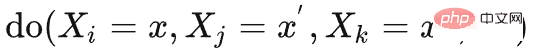 est le suivant :
est le suivant : 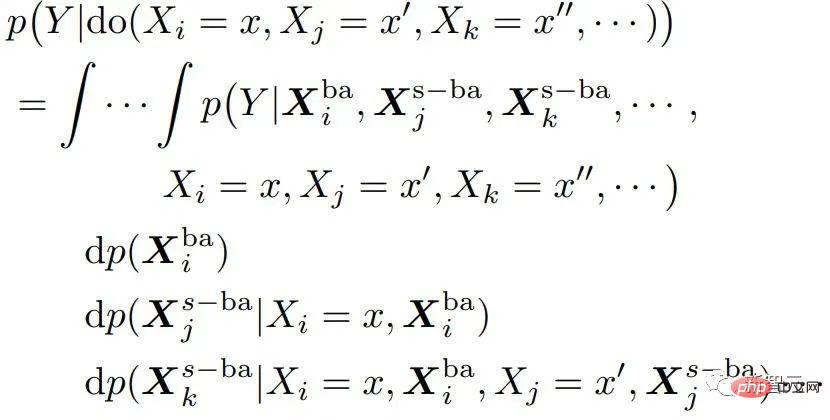
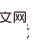 et
et 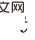 , l'effet causal de Do (o) peut être estimé par
, l'effet causal de Do (o) peut être estimé par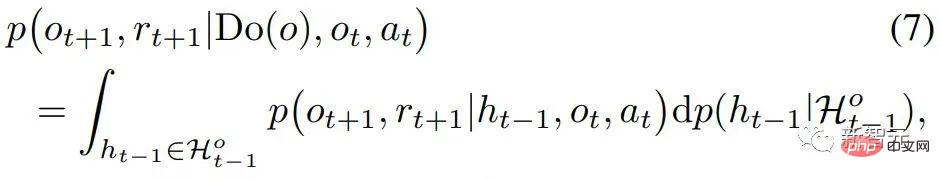
 ) à O (
) à O (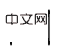 ). La prochaine étape consiste à tirer parti de la rareté des effets causals spatiaux (mentionnés au début de ce chapitre) pour réduire davantage le nombre d’interventions de manière exponentielle. Remplacer l'intervention sur une observation par l'intervention sur un sous-espace d'observation - c'est une idée courante pour profiter de la parcimonie pour accélérer les calculs (voir l'article original). Dans cet article, un algorithme d'inférence contrefactuelle rapide appelé Inférence contrefactuelle historique basée sur une arborescence (T-HCI) est développé, qui ne sera pas décrit en détail ici (voir le texte original pour plus de détails). En fait, de nombreux algorithmes d’inférence causale historique peuvent être développés sur la base du critère de la porte dérobée, et le T-HCI n’est que l’un d’entre eux. Le résultat final est la proposition 3 (IC grossier à fin). Si
). La prochaine étape consiste à tirer parti de la rareté des effets causals spatiaux (mentionnés au début de ce chapitre) pour réduire davantage le nombre d’interventions de manière exponentielle. Remplacer l'intervention sur une observation par l'intervention sur un sous-espace d'observation - c'est une idée courante pour profiter de la parcimonie pour accélérer les calculs (voir l'article original). Dans cet article, un algorithme d'inférence contrefactuelle rapide appelé Inférence contrefactuelle historique basée sur une arborescence (T-HCI) est développé, qui ne sera pas décrit en détail ici (voir le texte original pour plus de détails). En fait, de nombreux algorithmes d’inférence causale historique peuvent être développés sur la base du critère de la porte dérobée, et le T-HCI n’est que l’un d’entre eux. Le résultat final est la proposition 3 (IC grossier à fin). Si , le nombre d'interventions pour l'IC grossier à fin est de
, le nombre d'interventions pour l'IC grossier à fin est de ).
). 
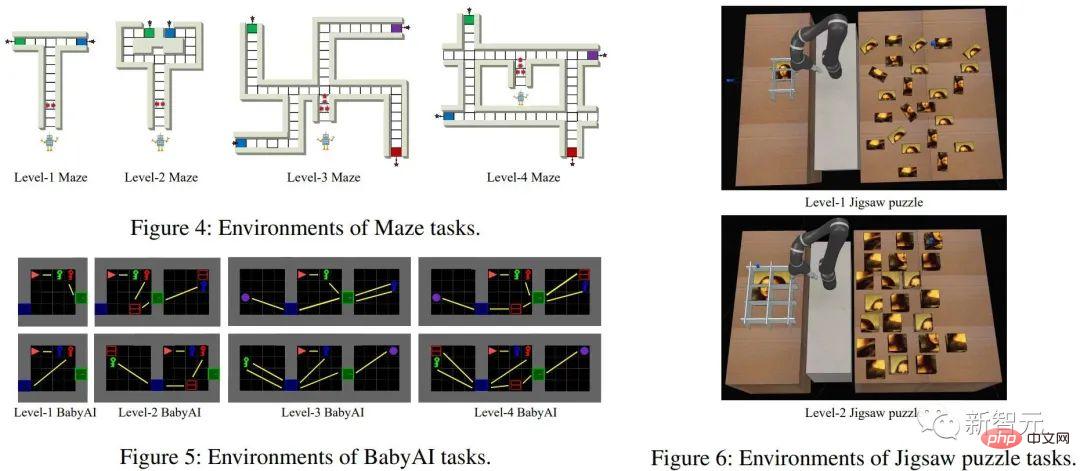
Vérification
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1369
1369
 52
52
 Comment changer la taille d'une liste de bootstrap?
Apr 07, 2025 am 10:45 AM
Comment changer la taille d'une liste de bootstrap?
Apr 07, 2025 am 10:45 AM
La taille d'une liste d'amorçage dépend de la taille du conteneur qui contient la liste, pas de la liste elle-même. L'utilisation du système de grille de bootstrap ou de Flexbox peut contrôler la taille du conteneur, redimentant ainsi indirectement les éléments de la liste.
 Comment implémenter la nidification des listes de bootstrap?
Apr 07, 2025 am 10:27 AM
Comment implémenter la nidification des listes de bootstrap?
Apr 07, 2025 am 10:27 AM
Les listes imbriquées dans Bootstrap nécessitent l'utilisation du système de grille de bootstrap pour contrôler le style. Tout d'abord, utilisez la couche extérieure & lt; ul & gt; et & lt; li & gt; Pour créer une liste, alors enveloppez la liste des calques intérieure dans & lt; div class = & quot; row & gt; et ajouter & lt; div class = & quot; col-md-6 & quot; & gt; à la liste des calques intérieure pour spécifier que la liste des calques intérieure occupe la moitié de la largeur d'une ligne. De cette façon, la liste intérieure peut avoir la bonne
 Comment ajouter des icônes à la liste Bootstrap?
Apr 07, 2025 am 10:42 AM
Comment ajouter des icônes à la liste Bootstrap?
Apr 07, 2025 am 10:42 AM
Comment ajouter des icônes à la liste Bootstrap: fourre directement l'icône dans l'élément de liste & lt; li & gt;, en utilisant le nom de classe fourni par la bibliothèque d'icônes (comme Font Awesome). Utilisez la classe bootstrap pour aligner les icônes et le texte (par exemple, d-flex, justifier-content-between, align-items-center). Utilisez le composant Bootstrap Tag (badge) pour afficher les numéros ou l'état. Ajustez la position de l'icône (Flex-Direction: Row-Reverse;), Contrôlez le style (style CSS). Erreur commune: l'icône ne s'affiche pas (pas
 Quelle méthode est utilisée pour convertir les chaînes en objets dans vue.js?
Apr 07, 2025 pm 09:39 PM
Quelle méthode est utilisée pour convertir les chaînes en objets dans vue.js?
Apr 07, 2025 pm 09:39 PM
Lors de la conversion des chaînes en objets dans vue.js, JSON.Parse () est préféré pour les chaînes JSON standard. Pour les chaînes JSON non standard, la chaîne peut être traitée en utilisant des expressions régulières et réduisez les méthodes en fonction du format ou du codé décodé par URL. Sélectionnez la méthode appropriée en fonction du format de chaîne et faites attention aux problèmes de sécurité et d'encodage pour éviter les bogues.
 Comment enregistrer les composants exportés par défaut d'exportation en Vue
Apr 07, 2025 pm 06:24 PM
Comment enregistrer les composants exportés par défaut d'exportation en Vue
Apr 07, 2025 pm 06:24 PM
Question: Comment enregistrer un composant VUE exporté via l'exportation par défaut? Réponse: Il existe trois méthodes d'enregistrement: Enregistrement global: utilisez la méthode Vue.Component () pour vous inscrire en tant que composant global. Inscription locale: Inscrivez-vous dans l'option Composants, disponible uniquement dans le composant actuel et ses sous-composants. Enregistrement dynamique: utilisez la méthode Vue.Component () pour vous inscrire après le chargement du composant.
 Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
L'optimisation des performances MySQL doit commencer à partir de trois aspects: configuration d'installation, indexation et optimisation des requêtes, surveillance et réglage. 1. Après l'installation, vous devez ajuster le fichier my.cnf en fonction de la configuration du serveur, tel que le paramètre innodb_buffer_pool_size, et fermer query_cache_size; 2. Créez un index approprié pour éviter les index excessifs et optimiser les instructions de requête, telles que l'utilisation de la commande Explication pour analyser le plan d'exécution; 3. Utilisez le propre outil de surveillance de MySQL (ShowProcessList, Showstatus) pour surveiller la santé de la base de données, et sauvegarde régulièrement et organisez la base de données. Ce n'est qu'en optimisant en continu ces étapes que les performances de la base de données MySQL peuvent être améliorées.
 Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Géospatial de Laravel: optimisation des cartes interactives et de grandes quantités de données
Apr 08, 2025 pm 12:24 PM
Traiter efficacement 7 millions d'enregistrements et créer des cartes interactives avec la technologie géospatiale. Cet article explore comment traiter efficacement plus de 7 millions d'enregistrements en utilisant Laravel et MySQL et les convertir en visualisations de cartes interactives. Exigences initiales du projet de défi: extraire des informations précieuses en utilisant 7 millions d'enregistrements dans la base de données MySQL. Beaucoup de gens considèrent d'abord les langages de programmation, mais ignorent la base de données elle-même: peut-il répondre aux besoins? La migration des données ou l'ajustement structurel est-il requis? MySQL peut-il résister à une charge de données aussi importante? Analyse préliminaire: les filtres et les propriétés clés doivent être identifiés. Après analyse, il a été constaté que seuls quelques attributs étaient liés à la solution. Nous avons vérifié la faisabilité du filtre et établi certaines restrictions pour optimiser la recherche. Recherche de cartes basée sur la ville
 Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Comment résoudre MySQL ne peut pas être démarré
Apr 08, 2025 pm 02:21 PM
Il existe de nombreuses raisons pour lesquelles la startup MySQL échoue, et elle peut être diagnostiquée en vérifiant le journal des erreurs. Les causes courantes incluent les conflits de port (vérifier l'occupation du port et la configuration de modification), les problèmes d'autorisation (vérifier le service exécutant les autorisations des utilisateurs), les erreurs de fichier de configuration (vérifier les paramètres des paramètres), la corruption du répertoire de données (restaurer les données ou reconstruire l'espace de la table), les problèmes d'espace de la table InNODB (vérifier les fichiers IBDATA1), la défaillance du chargement du plug-in (vérification du journal des erreurs). Lors de la résolution de problèmes, vous devez les analyser en fonction du journal d'erreur, trouver la cause profonde du problème et développer l'habitude de sauvegarder régulièrement les données pour prévenir et résoudre des problèmes.



