
L'optimisation du réseau neuronal pendant l'entraînement consiste d'abord à estimer l'erreur de l'état actuel du modèle, puis afin de réduire l'erreur de la prochaine évaluation, il est nécessaire de mettre à jour les poids à l'aide d'une fonction qui peut représenter l'erreur. Cette fonction est appelée fonction de perte.

Le choix de la fonction de perte est lié au problème de modélisation prédictive spécifique (tel que la classification ou la régression) que le modèle de réseau neuronal apprend à partir d'exemples. Dans cet article, nous présenterons certaines fonctions de perte couramment utilisées, notamment :
Modèle principal de prédiction de régression est utilisé pour prédire des valeurs continues. Nous allons donc utiliser la fonction make_regression() de scikit-learn pour générer des données simulées et utiliser ces données pour construire un modèle de régression.
Nous générerons 20 fonctionnalités d'entrée : 10 d'entre elles seront significatives, mais 10 ne seront pas pertinentes pour le problème.
Et générez aléatoirement 1 000 exemples. Et spécifiez une graine aléatoire, afin que les mêmes 1 000 exemples soient générés chaque fois que vous exécutez le code.

La mise à l'échelle des variables d'entrée et de sortie à valeur réelle dans une plage raisonnable améliore souvent les performances des réseaux de neurones. Nous devons donc normaliser les données.
StandardScaler est également disponible dans la bibliothèque scikit-learn, pour simplifier le problème, nous mettrons à l'échelle toutes les données avant de les diviser en ensembles d'entraînement et de test.

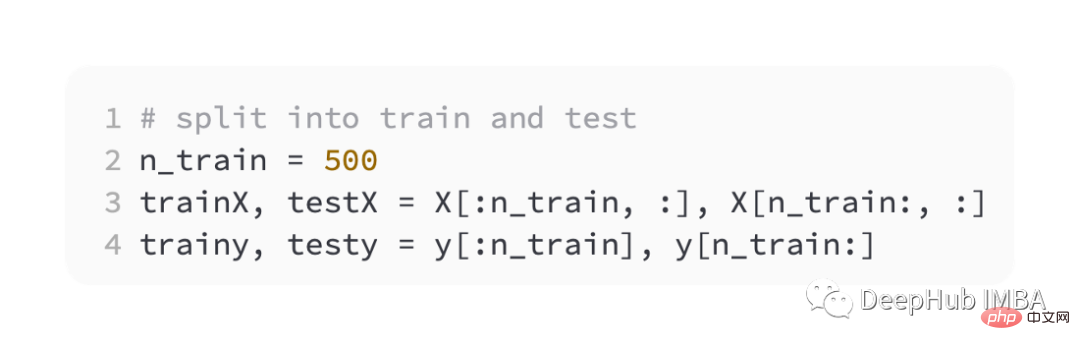
Divisez ensuite les ensembles de formation et de validation à parts égales
Pour introduire différentes fonctions de perte, nous développerons un petit modèle de perceptron multicouche (MLP).
Selon la définition du problème, il y a 20 fonctionnalités en entrée, qui passent par notre modèle. Une valeur réelle est nécessaire pour prédire, donc la couche de sortie aura un nœud.

Nous utilisons SGD pour l'optimisation et avons un taux d'apprentissage de 0,01 et un élan de 0,9, qui sont tous deux des valeurs par défaut raisonnables. La formation sera menée pendant 100 époques, l'ensemble de tests sera évalué à la fin de chaque étape et la courbe d'apprentissage sera tracée.

Une fois le modèle terminé, la fonction de perte peut être introduite :
Le problème de régression le plus couramment utilisé est la perte d'erreur quadratique moyenne (MSE). Il s'agit de la fonction de perte préférée dans le cadre de l'inférence du maximum de vraisemblance lorsque la distribution de la variable cible est gaussienne. Vous ne devriez donc passer à d’autres fonctions de perte que si vous avez une meilleure raison.
Si "mse" ou "mean_squared_error" est spécifié comme fonction de perte lors de la compilation du modèle dans Keras, la fonction de perte d'erreur quadratique moyenne est utilisée.

Le code ci-dessous est un exemple complet du problème de régression ci-dessus.
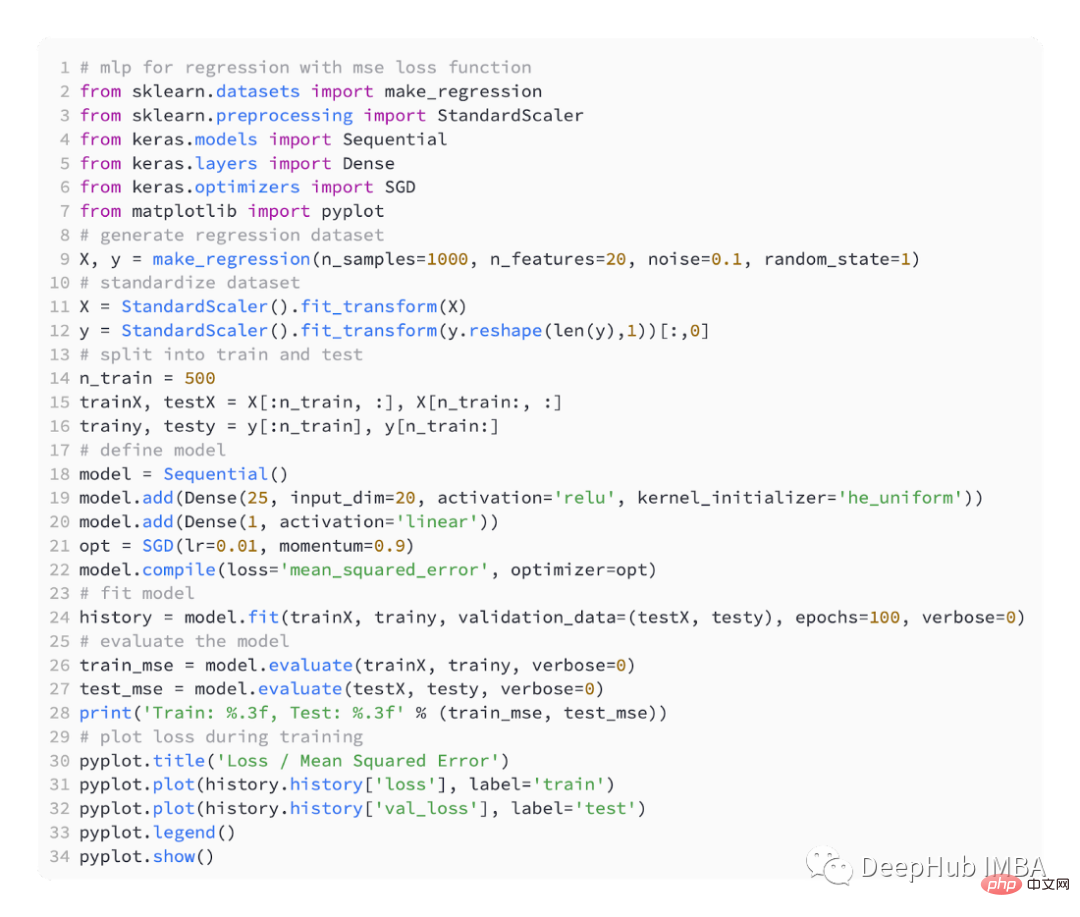
Dans la première étape de l'exécution de l'exemple, l'erreur quadratique moyenne des ensembles de données d'entraînement et de test du modèle est imprimée. Parce que 3 décimales sont conservées, elle est affichée sous la forme 0,000

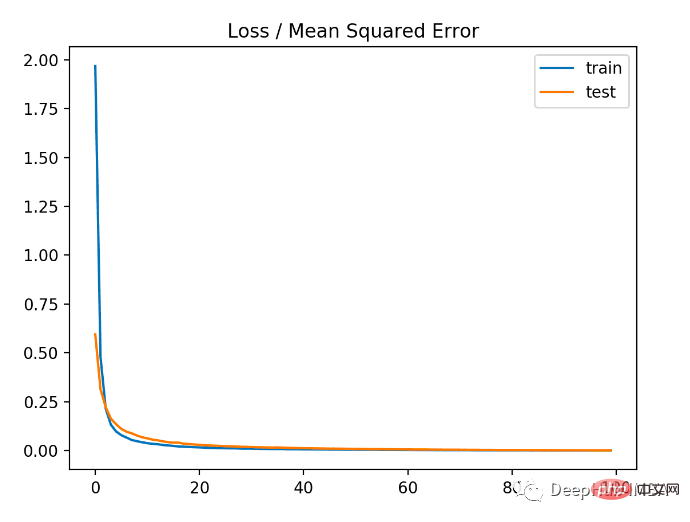
Comme vous le souhaitez. peut le voir sur l'image ci-dessous. Il s'avère que le modèle converge assez rapidement et que les performances de formation et de test restent inchangées. En fonction des performances et des propriétés de convergence du modèle, l'erreur quadratique moyenne est un bon choix pour les problèmes de régression.
Dans les problèmes de régression avec une large plage de valeurs, il n'est peut-être pas souhaitable de pénaliser le modèle autant que l'erreur quadratique moyenne lors de la prédiction de valeurs élevées. Ainsi, l’erreur quadratique moyenne peut être calculée en calculant d’abord le logarithme népérien de chaque valeur prédite. Cette perte est appelée MSLE, ou erreur logarithmique moyenne.
Cela a pour effet d'atténuer l'effet de pénalité lorsqu'il y a une grande différence dans les valeurs prédites. Il peut s'agir d'une mesure de perte plus appropriée lorsque le modèle prédit directement des quantités non mises à l'échelle.
Utilisation de "mean_squared_logarithmic_error" comme fonction de perte dans keras

L'exemple ci-dessous est le code complet utilisant la fonction de perte MSLE.

Le modèle a un MSE légèrement pire sur les ensembles de données d'entraînement et de test. En effet, la distribution de la variable cible est une distribution gaussienne standard, ce qui signifie que notre fonction de perte n'est peut-être pas très adaptée à ce problème.

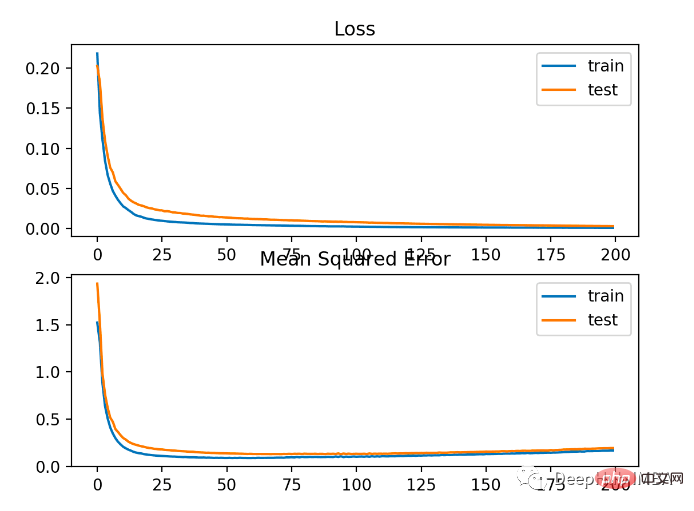
La figure ci-dessous montre la comparaison de chaque époque d'entraînement. Le MSE converge bien, mais le MSE peut être suradapté car il diminue à partir de l'époque 20 pour changer et commence à augmenter.
Selon le problème de régression, la distribution de la variable cible peut être principalement gaussienne, mais peut contenir des valeurs aberrantes, telles que des valeurs grandes ou petites éloignées de la moyenne.
Dans ce cas, l'erreur absolue moyenne ou la perte MAE est une fonction de perte appropriée car elle est plus robuste aux valeurs aberrantes. Calculé comme une moyenne, en tenant compte de la différence absolue entre les valeurs réelles et prédites.
Utilisation de la fonction de perte "mean_absolute_error"

Voici le code complet utilisant MAE

Les résultats sont les suivants

Comme vous pouvez le voir dans la figure ci-dessous, MAE converge mais il a un processus cahoteux. MAE n’est pas non plus très adapté dans ce cas car la variable cible est une fonction gaussienne sans grandes valeurs aberrantes.
Un problème de classification binaire est l'une des deux étiquettes d'un problème de modélisation prédictive. Ce problème est défini comme prédisant la valeur de la première ou de la deuxième classe comme 0 ou 1, et est généralement implémenté comme prédisant la probabilité d'appartenir à la valeur de classe 1.
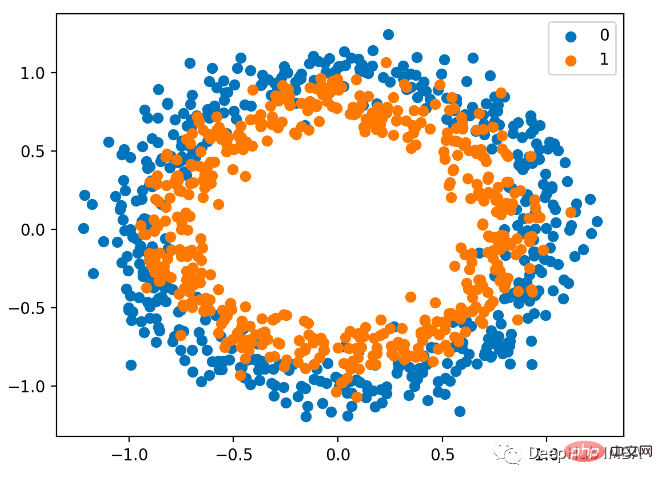
Nous utilisons également sklearn pour générer des données. Ici, nous utilisons un problème de cercle. Il comporte un plan bidimensionnel et deux cercles concentriques. Les points sur le cercle extérieur appartiennent à la classe 0 et les points sur le cercle intérieur appartiennent à la classe 1. . Pour rendre l'apprentissage plus difficile, nous ajoutons également du bruit statistique aux échantillons. La taille de l'échantillon est de 1 000 et 10 % de bruit statistique sont ajoutés.

Un nuage de points d'un ensemble de données peut nous aider à comprendre le problème que nous modélisons. Vous trouverez ci-dessous un exemple complet.

Le nuage de points est le suivant, où la variable d'entrée détermine la position du point et la couleur est la valeur de classe. 0 est bleu et 1 est orange.
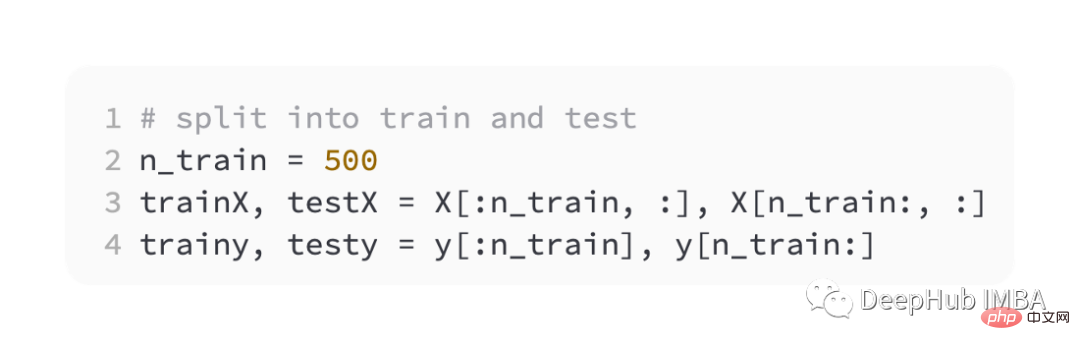
Voici toujours la moitié pour la formation et l'autre moitié pour les tests,
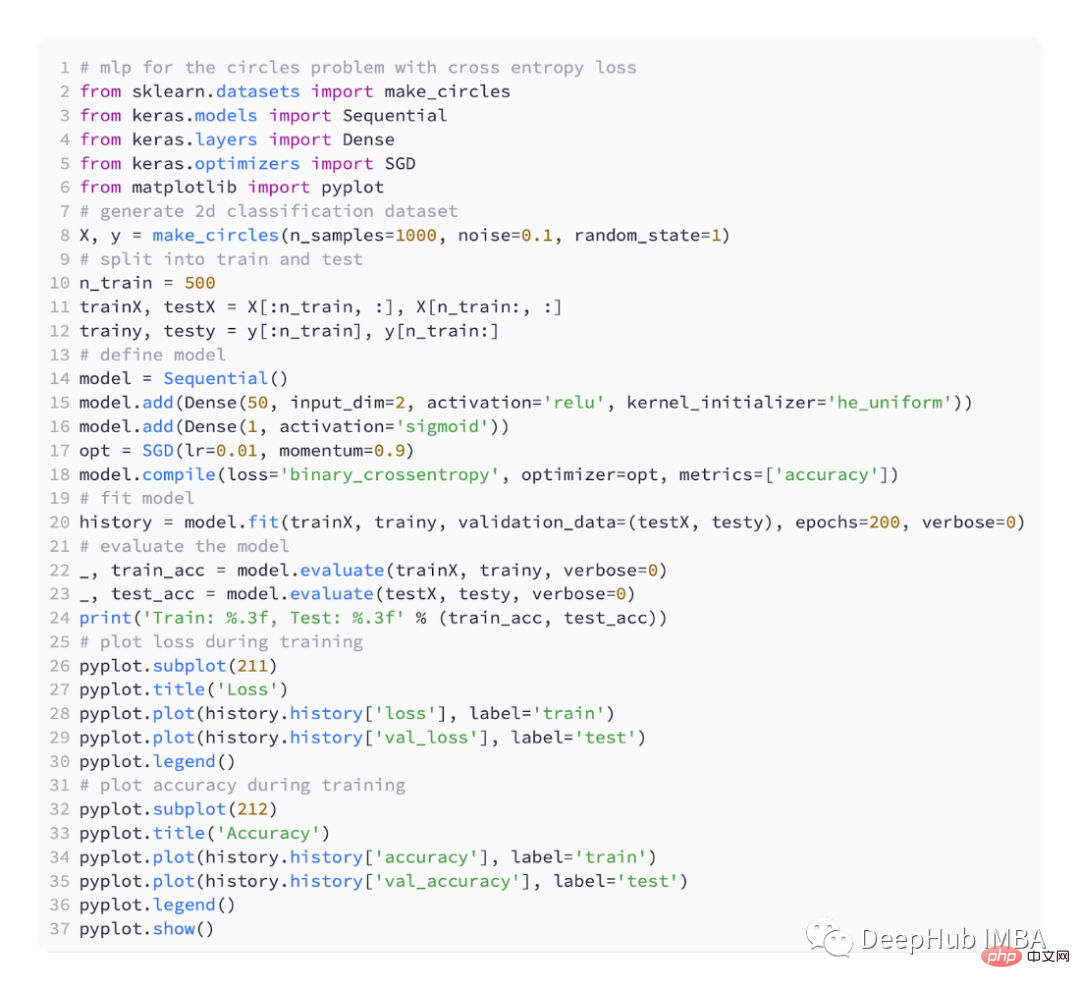
Nous définissons toujours un modèle MLP simple,

utilisant l'optimisation SGD, le taux d'apprentissage est de 0,01 et l'élan est de 0,99.

Le modèle est entraîné pour 200 tours d'ajustement et les performances du modèle sont évaluées en termes de perte et de précision.

BCE est la fonction de perte par défaut utilisée pour résoudre les problèmes de classification binaire. Dans le cadre d’inférence du maximum de vraisemblance, c’est la fonction de perte de choix. Pour les prédictions de type 1, l'entropie croisée calcule un score qui résume la différence moyenne entre les distributions de probabilité réelle et prédite.
Lors de la compilation du modèle Keras, binaire_crossentropy peut être spécifié comme fonction de perte.

Pour prédire la probabilité de classe 1, la couche de sortie doit contenir un nœud et une activation 'sigmoïde'.

Voici le code complet :
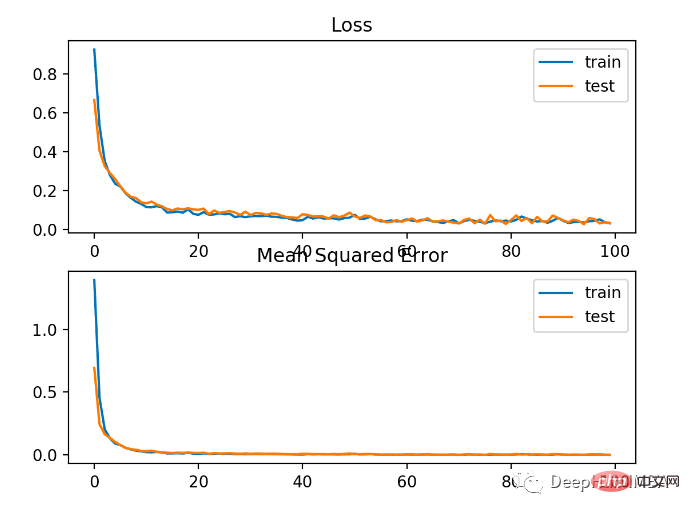
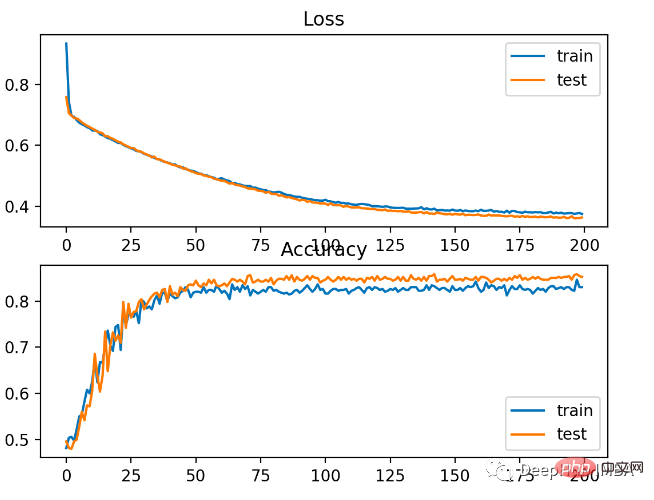
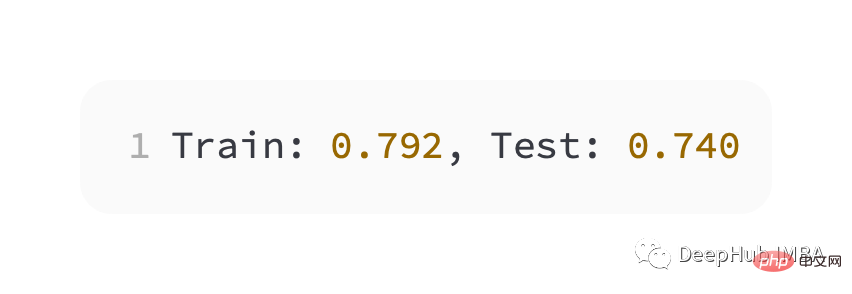
Le modèle a relativement bien appris le problème, avec une précision de 83% et une précision de 85% sur l'ensemble de données de test. Il existe un certain degré de chevauchement entre les scores, ce qui indique que le modèle n’est ni surajusté ni sous-ajusté.
Comme le montre l'image ci-dessous, l'effet d'entraînement est très bon. Étant donné que l'erreur entre les distributions de probabilité est continue, le tracé des pertes est fluide, tandis que le tracé linéaire de précision présente des irrégularités, car les exemples des ensembles d'entraînement et de test ne peuvent être prédits que comme étant corrects ou incorrects, fournissant ainsi des informations moins granulaires.
Le modèle Support Vector Machine (SVM) utilise la fonction de perte de charnière comme alternative à l'entropie croisée pour résoudre les problèmes de classification binaire.
La valeur cible est dans l'ensemble [-1, 1] , destiné à être utilisé avec la classification binaire. La charnière obtiendra des erreurs plus importantes si les valeurs de classe réelles et prédites ont des signes différents. C'est parfois mieux que l'entropie croisée sur les problèmes de classification binaire.
Dans un premier temps, nous devons modifier la valeur de la variable cible à l'ensemble {-1, 1}.

On l'appelle 'charnière' en keras.

Dans la couche de sortie du réseau, un seul nœud de la fonction d'activation tanh doit être utilisé pour générer une valeur unique comprise entre -1 et 1.

Voici le code complet :

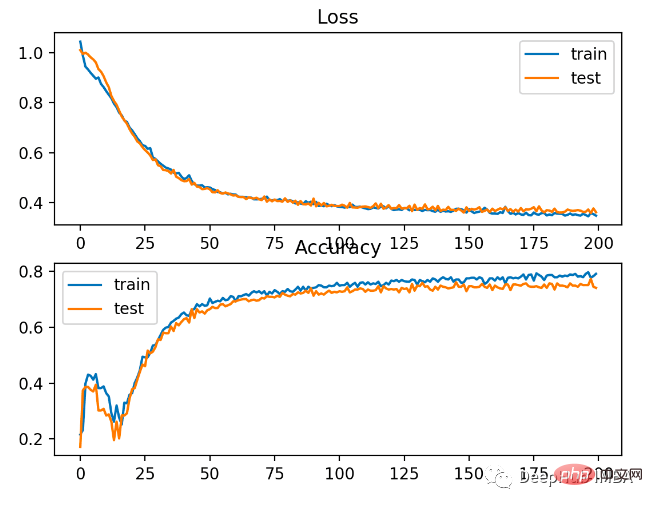
Performances légèrement moins bonnes que l'entropie croisée, moins de 80 % de précision sur les ensembles d'entraînement et de test.
Comme vous pouvez le voir sur la figure ci-dessous, le modèle a convergé et le graphique de précision de la classification montre qu'il a également convergé.
Vous pouvez voir que BCE est meilleur pour ce problème. La raison possible ici est que nous avons quelques points de bruit
.Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Les huit fonctions les plus couramment utilisées dans Excel
Les huit fonctions les plus couramment utilisées dans Excel
 Comment connecter le haut débit au serveur
Comment connecter le haut débit au serveur
 Comment configurer l'espace virtuel jsp
Comment configurer l'espace virtuel jsp
 Quels types de fichiers peuvent être identifiés sur la base
Quels types de fichiers peuvent être identifiés sur la base
 Comment gérer le ralentissement de l'ordinateur et la lenteur des réponses
Comment gérer le ralentissement de l'ordinateur et la lenteur des réponses
 nom complet de l'application
nom complet de l'application
 moyens visibles
moyens visibles
 Solutions aux exceptions logicielles inconnues dans les applications informatiques
Solutions aux exceptions logicielles inconnues dans les applications informatiques
 Utilisation de typedef en langage C
Utilisation de typedef en langage C