Périphériques technologiques
IA
Dix méthodes de mesure de distance couramment utilisées en apprentissage automatique
Dix méthodes de mesure de distance couramment utilisées en apprentissage automatique
La métrique de distance est la base des algorithmes d'apprentissage supervisé et non supervisé, y compris le k-voisin le plus proche, la machine à vecteurs de support et le clustering k-means, etc.
Le choix de la métrique de distance affecte nos résultats d'apprentissage automatique, il est donc important de déterminer quelle métrique est la mieux adaptée au problème. Par conséquent, nous devons être prudents lorsque nous décidons quelle méthode de mesure utiliser. Mais avant de prendre une décision, nous devons comprendre comment fonctionne la mesure de distance et quelles mesures nous pouvons choisir.
Cet article présentera brièvement les méthodes de mesure de distance couramment utilisées, comment elles fonctionnent, comment les calculer en Python et quand les utiliser. Cela approfondit les connaissances et la compréhension et améliore les algorithmes et les résultats d’apprentissage automatique.
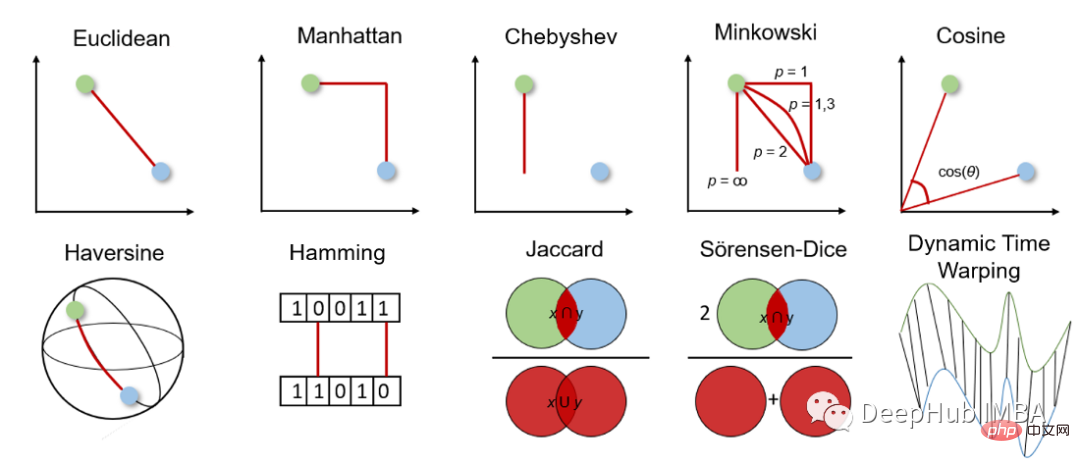
Avant d’approfondir les différentes mesures de distance, ayons d’abord une idée générale de leur fonctionnement et de la manière de choisir la mesure appropriée.
La métrique de distance est utilisée pour calculer la différence entre deux objets dans un espace problématique donné, c'est-à-dire les caractéristiques de l'ensemble de données. Cette distance peut ensuite être utilisée pour déterminer la similarité entre les entités : plus la distance est petite, plus les entités sont similaires.
Pour la mesure de distance, nous pouvons choisir entre la mesure de distance géométrique et la mesure de distance statistique. La mesure de distance à choisir dépend du type de données. Les entités peuvent être de différents types de données (par exemple, valeurs réelles, valeurs booléennes, valeurs catégorielles), et les données peuvent être multidimensionnelles ou constituées de données géospatiales.
Mesure de la distance géométrique
1. Distance euclidienne Distance euclidienne
La distance euclidienne mesure la distance la plus courte entre deux vecteurs à valeur réelle. En raison de son caractère intuitif, de sa simplicité d'utilisation et de ses bons résultats dans de nombreux cas d'utilisation, il s'agit de la métrique de distance la plus couramment utilisée et de la métrique de distance par défaut pour de nombreuses applications.
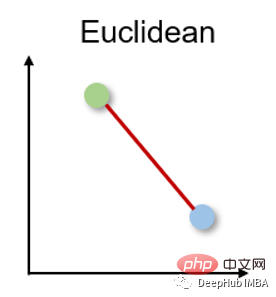
La distance euclidienne peut aussi être appelée norme l2, et sa méthode de calcul est la suivante :
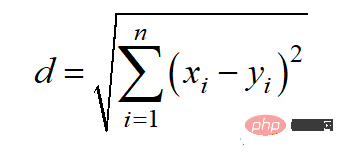
Le code Python est le suivant
from scipy.spatial import distance distance.euclidean(vector_1, vector_2)
La distance euclidienne présente deux inconvénients principaux. Premièrement, les mesures de distance ne fonctionnent pas avec des données de dimensions supérieures à l’espace 2D ou 3D. Deuxièmement, si nous ne normalisons pas et/ou ne normalisons pas les caractéristiques, les distances peuvent être faussées par unités.
2. Distance de Manhattan
La distance de Manhattan est également appelée distance en taxi ou en pâté de maisons, car la distance entre deux vecteurs à valeur réelle est calculée sur la base du fait qu'une personne ne peut se déplacer qu'à angle droit. Cette mesure de distance est souvent utilisée pour les attributs discrets et binaires afin d'obtenir de véritables chemins.
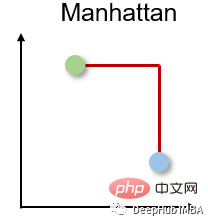
La distance de Manhattan est basée sur la norme l1, et la formule de calcul est :
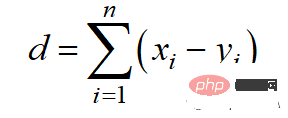
Le code Python est le suivant
from scipy.spatial import distance distance.cityblock(vector_1, vector_2)
La distance de Manhattan présente deux inconvénients principaux. Elle n’est pas aussi intuitive que la distance euclidienne dans un espace de grande dimension et ne montre pas non plus le chemin le plus court possible. Même si cela ne pose pas de problème, nous devons être conscients qu’il ne s’agit pas de la distance la plus courte.
3. Distance de Chebyshev Distance de Chebyshev
La distance de Chebyshev est également appelée distance en damier car c'est la distance maximale dans n'importe quelle dimension entre deux vecteurs à valeur réelle. Il est couramment utilisé dans la logistique d’entrepôt, où le chemin le plus long détermine le temps nécessaire pour se rendre d’un point à un autre.
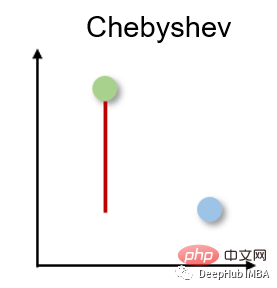
La distance de Chebyshev est calculée selon la norme l -infini :
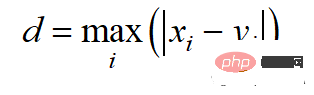
Le code Python est le suivant
from scipy.spatial import distance distance.chebyshev(vector_1, vector_2)
La distance de Chebyshev n'a que des cas d'utilisation très spécifiques et est donc rarement utilisée.
4. Distance de Minkowski Distance de Minkowski
La distance de Minkowski est la forme généralisée de la mesure de distance ci-dessus. Il peut être utilisé pour les mêmes cas d’utilisation tout en offrant une grande flexibilité. Nous pouvons choisir la valeur p pour trouver la mesure de distance la plus appropriée.
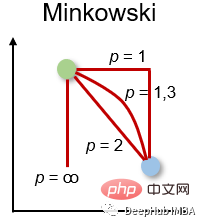
La méthode de calcul de la distance de Minkowski est la suivante :
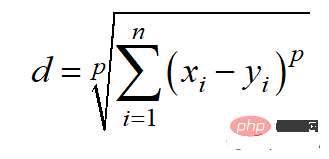
Le code Python est le suivant
from scipy.spatial import distance distance.minkowski(vector_1, vector_2, p)
Étant donné que la distance de Minkowski représente différentes mesures de distance, elle présente les mêmes principaux inconvénients qu'eux, comme dans les grandes dimensions. Problèmes avec l'espace et la dépendance à l'égard d'unités caractéristiques. De plus, la flexibilité des valeurs p peut également être un inconvénient, car elle peut réduire l'efficacité des calculs puisque plusieurs calculs sont nécessaires pour trouver la valeur p correcte.
5. Similitude cosinus et distance Similitude cosinus
La similarité cosinus est une mesure de direction. Sa taille est déterminée par le cosinus entre deux vecteurs et ignore la taille du vecteur. La similarité cosinusoïdale est souvent utilisée dans les grandes dimensions où la taille des données n'a pas d'importance, par exemple dans les systèmes de recommandation ou l'analyse de texte.
余弦相似度可以介于-1(相反方向)和1(相同方向)之间，计算方法为:
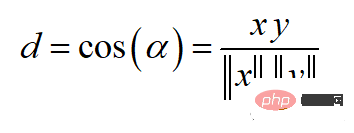
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度，位于0(相似值)和1(不同值)之间。
Python代码如下
from scipy.spatial import distance distance.cosine(vector_1, vector_2)
余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此，没有充分考虑到值的差异。
6、半正矢距离 Haversine distance
半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航，其中经度和纬度和曲率对计算都有影响。
半正矢距离的公式如下：
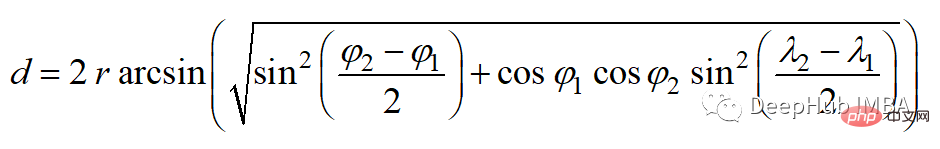
其中r为球面半径，φ和λ为经度和纬度。
Python代码如下
from sklearn.metrics.pairwise import haversine_distances haversine_distances([vector_1, vector_2])
半正矢距离的主要缺点是假设是一个球体，而这种情况很少出现。
7、汉明距离
汉明距离衡量两个二进制向量或字符串之间的差异。
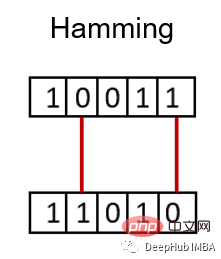
对向量按元素进行比较，并对差异的数量进行平均。如果两个向量相同，得到的距离是0之间，如果两个向量完全不同，得到的距离是1。
Python代码如下
from scipy.spatial import distance distance.hamming(vector_1, vector_2)
汉明距离有两个主要缺点。距离测量只能比较相同长度的向量，它不能给出差异的大小。所以当差异的大小很重要时，不建议使用汉明距离。
统计距离测量
统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。
8、杰卡德指数和距离 Jaccard Index
Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较，或者根据单词的重叠来比较文档中的文本模式。
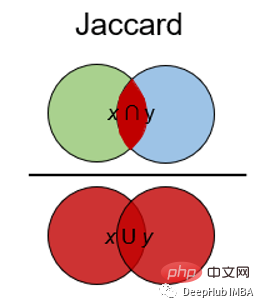
Jaccard距离的计算方法为:
Python代码如下
from scipy.spatial import distance distance.jaccard(vector_1, vector_2)
Jaccard指数和距离的主要缺点是，它受到数据规模的强烈影响，即每个项目的权重与数据集的规模成反比。
9、Sorensen-Dice指数
Sörensen-Dice指数类似于Jaccard指数，它可以衡量的是样本集的相似性和多样性。该指数更直观，因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。
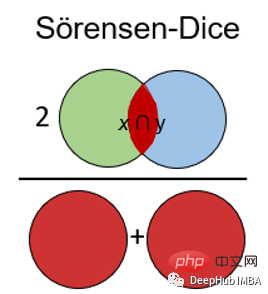
计算公式如下：
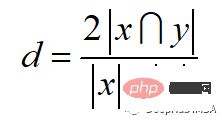
Python代码如下
from scipy.spatial import distance distance.dice(vector_1, vector_2)
它的主要缺点也是受数据集大小的影响很大。
10、动态时间规整 Dynamic Time Warping
动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例，如语音识别或异常检测。
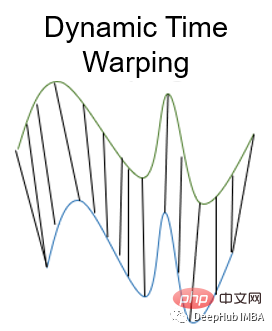
为什么我们需要一个为时间序列进行距离测量的度量呢？如果时间序列长度不同或失真，则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移，那么尽管时间序列非常相似，但欧几里得距离会表现出很大的差异。
动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时，这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离，该路径必须满足以下条件：
- 边界条件:弯曲路径在两个时间序列的起始点和结束点开始和结束
- 单调性条件:保持点的时间顺序，避免时间倒流
- 连续条件:路径转换限制在相邻的时间点上，避免时间跳跃
- 整经窗口条件(可选):允许的点落入给定宽度的整经窗口
- 坡度条件(可选):限制弯曲路径坡度，避免极端运动
我们可以使用 Python 中的 fastdtw 包：
from scipy.spatial.distance import euclidean from fastdtw import fastdtw distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)
动态时间规整的一个主要缺点是与其他距离测量方法相比，它的计算工作量相对较高。
总结
在这篇文章中，简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的，如何在Python中实现它们，以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量，请留言告诉我。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Outils d'IA chauds
Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes
AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.
Undress AI Tool
Images de déshabillage gratuites
Clothoff.io
Dissolvant de vêtements AI
Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !
Article chaud
Outils chauds
Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit
SublimeText3 version chinoise
Version chinoise, très simple à utiliser
Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP
Dreamweaver CS6
Outils de développement Web visuel
SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
Sujets chauds
Cet article vous amènera à comprendre SHAP : explication du modèle pour l'apprentissage automatique
Jun 01, 2024 am 10:58 AM
Dans les domaines de l’apprentissage automatique et de la science des données, l’interprétabilité des modèles a toujours été au centre des préoccupations des chercheurs et des praticiens. Avec l'application généralisée de modèles complexes tels que l'apprentissage profond et les méthodes d'ensemble, la compréhension du processus décisionnel du modèle est devenue particulièrement importante. Explainable AI|XAI contribue à renforcer la confiance dans les modèles d'apprentissage automatique en augmentant la transparence du modèle. L'amélioration de la transparence des modèles peut être obtenue grâce à des méthodes telles que l'utilisation généralisée de plusieurs modèles complexes, ainsi que les processus décisionnels utilisés pour expliquer les modèles. Ces méthodes incluent l'analyse de l'importance des caractéristiques, l'estimation de l'intervalle de prédiction du modèle, les algorithmes d'interprétabilité locale, etc. L'analyse de l'importance des fonctionnalités peut expliquer le processus de prise de décision du modèle en évaluant le degré d'influence du modèle sur les fonctionnalités d'entrée. Estimation de l’intervalle de prédiction du modèle
Identifier le surapprentissage et le sous-apprentissage grâce à des courbes d'apprentissage
Apr 29, 2024 pm 06:50 PM
Cet article présentera comment identifier efficacement le surajustement et le sous-apprentissage dans les modèles d'apprentissage automatique grâce à des courbes d'apprentissage. Sous-ajustement et surajustement 1. Surajustement Si un modèle est surentraîné sur les données de sorte qu'il en tire du bruit, alors on dit que le modèle est en surajustement. Un modèle surajusté apprend chaque exemple si parfaitement qu'il classera mal un exemple inédit/inédit. Pour un modèle surajusté, nous obtiendrons un score d'ensemble d'entraînement parfait/presque parfait et un score d'ensemble/test de validation épouvantable. Légèrement modifié : "Cause du surajustement : utilisez un modèle complexe pour résoudre un problème simple et extraire le bruit des données. Parce qu'un petit ensemble de données en tant qu'ensemble d'entraînement peut ne pas représenter la représentation correcte de toutes les données."
Transparent! Une analyse approfondie des principes des principaux modèles de machine learning !
Apr 12, 2024 pm 05:55 PM
En termes simples, un modèle d’apprentissage automatique est une fonction mathématique qui mappe les données d’entrée à une sortie prédite. Plus précisément, un modèle d'apprentissage automatique est une fonction mathématique qui ajuste les paramètres du modèle en apprenant à partir des données d'entraînement afin de minimiser l'erreur entre la sortie prédite et la véritable étiquette. Il existe de nombreux modèles dans l'apprentissage automatique, tels que les modèles de régression logistique, les modèles d'arbre de décision, les modèles de machines à vecteurs de support, etc. Chaque modèle a ses types de données et ses types de problèmes applicables. Dans le même temps, il existe de nombreux points communs entre les différents modèles, ou il existe une voie cachée pour l’évolution du modèle. En prenant comme exemple le perceptron connexionniste, en augmentant le nombre de couches cachées du perceptron, nous pouvons le transformer en un réseau neuronal profond. Si une fonction noyau est ajoutée au perceptron, elle peut être convertie en SVM. celui-ci
L'évolution de l'intelligence artificielle dans l'exploration spatiale et l'ingénierie des établissements humains
Apr 29, 2024 pm 03:25 PM
Dans les années 1950, l’intelligence artificielle (IA) est née. C’est à ce moment-là que les chercheurs ont découvert que les machines pouvaient effectuer des tâches similaires à celles des humains, comme penser. Plus tard, dans les années 1960, le Département américain de la Défense a financé l’intelligence artificielle et créé des laboratoires pour poursuivre son développement. Les chercheurs trouvent des applications à l’intelligence artificielle dans de nombreux domaines, comme l’exploration spatiale et la survie dans des environnements extrêmes. L'exploration spatiale est l'étude de l'univers, qui couvre l'ensemble de l'univers au-delà de la terre. L’espace est classé comme environnement extrême car ses conditions sont différentes de celles de la Terre. Pour survivre dans l’espace, de nombreux facteurs doivent être pris en compte et des précautions doivent être prises. Les scientifiques et les chercheurs pensent qu'explorer l'espace et comprendre l'état actuel de tout peut aider à comprendre le fonctionnement de l'univers et à se préparer à d'éventuelles crises environnementales.
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
Flash Attention est-il stable ? Meta et Harvard ont constaté que les écarts de poids de leur modèle fluctuaient de plusieurs ordres de grandeur.
May 30, 2024 pm 01:24 PM
MetaFAIR s'est associé à Harvard pour fournir un nouveau cadre de recherche permettant d'optimiser le biais de données généré lors de l'apprentissage automatique à grande échelle. On sait que la formation de grands modèles de langage prend souvent des mois et utilise des centaines, voire des milliers de GPU. En prenant comme exemple le modèle LLaMA270B, sa formation nécessite un total de 1 720 320 heures GPU. La formation de grands modèles présente des défis systémiques uniques en raison de l’ampleur et de la complexité de ces charges de travail. Récemment, de nombreuses institutions ont signalé une instabilité dans le processus de formation lors de la formation des modèles d'IA générative SOTA. Elles apparaissent généralement sous la forme de pics de pertes. Par exemple, le modèle PaLM de Google a connu jusqu'à 20 pics de pertes au cours du processus de formation. Le biais numérique est à l'origine de cette imprécision de la formation,
Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
L'ensemble de données ScienceAI Question Answering (QA) joue un rôle essentiel dans la promotion de la recherche sur le traitement du langage naturel (NLP). Des ensembles de données d'assurance qualité de haute qualité peuvent non seulement être utilisés pour affiner les modèles, mais également évaluer efficacement les capacités des grands modèles linguistiques (LLM), en particulier la capacité à comprendre et à raisonner sur les connaissances scientifiques. Bien qu’il existe actuellement de nombreux ensembles de données scientifiques d’assurance qualité couvrant la médecine, la chimie, la biologie et d’autres domaines, ces ensembles de données présentent encore certaines lacunes. Premièrement, le formulaire de données est relativement simple, et la plupart sont des questions à choix multiples. Elles sont faciles à évaluer, mais limitent la plage de sélection des réponses du modèle et ne peuvent pas tester pleinement la capacité du modèle à répondre aux questions scientifiques. En revanche, les questions et réponses ouvertes
