 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Apprendre = s'adapter ? Le deep learning et les statistiques classiques sont-ils la même chose ?
Apprendre = s'adapter ? Le deep learning et les statistiques classiques sont-ils la même chose ?
Apprendre = s'adapter ? Le deep learning et les statistiques classiques sont-ils la même chose ?
Dans cet article, Boaz Barak, informaticien théoricien et professeur bien connu à l'Université Harvard, compare en détail les différences entre l'apprentissage profond et les statistiques classiques. Il estime que « si vous comprenez l'apprentissage profond uniquement d'un point de vue statistique, vous. ignorera les facteurs clés de son succès." ".
Le deep learning (ou l'apprentissage automatique en général) est souvent considéré comme de simples statistiques, c'est-à-dire qu'il s'agit fondamentalement du même concept que celui étudié par les statisticiens, mais il est décrit en utilisant une terminologie différente de celle des statistiques. Rob Tibshirani a un jour résumé ce « vocabulaire » intéressant ci-dessous :

Est-ce que quelque chose dans cette liste résonne vraiment ? Pratiquement toute personne impliquée dans l'apprentissage automatique sait que la plupart des termes figurant à droite du tableau publié par Tibshirani sont largement utilisés dans l'apprentissage automatique.
Si vous comprenez le deep learning uniquement d’un point de vue statistique, vous ignorerez les facteurs clés de son succès. Une évaluation plus appropriée de l’apprentissage profond est qu’il utilise des termes statistiques pour décrire des concepts complètement différents.
La bonne évaluation de l'apprentissage profond n'est pas qu'il utilise des mots différents pour décrire d'anciens termes statistiques, mais qu'il utilise ces termes pour décrire des processus complètement différents.
Cet article expliquera pourquoi les fondements du deep learning sont en réalité différents des statistiques, voire différents du machine learning classique. Cet article aborde d'abord la différence entre la tâche « explication » et la tâche « prédiction » lors de l'ajustement d'un modèle aux données. Deux scénarios du processus d'apprentissage sont ensuite discutés : 1. Ajustement de modèles statistiques en utilisant la minimisation empirique des risques. 2. Enseigner des compétences mathématiques aux étudiants ; Ensuite, l’article discute du scénario le plus proche de l’essence de l’apprentissage profond.
Alors que les mathématiques et le code pour l'apprentissage profond sont presque les mêmes que l'ajustement de modèles statistiques. Mais à un niveau plus profond, l’apprentissage profond s’apparente davantage à l’enseignement de compétences mathématiques aux étudiants. Et il devrait y avoir très peu de gens qui osent prétendre : je maîtrise complètement la théorie de l’apprentissage profond ! En fait, il est douteux qu’une telle théorie existe. Au lieu de cela, les différents aspects de l’apprentissage profond sont mieux compris sous différents angles, et les statistiques à elles seules ne peuvent pas fournir une image complète.
Cet article compare l'apprentissage profond et les statistiques. Les statistiques font ici spécifiquement référence aux « statistiques classiques » car elles sont étudiées depuis très longtemps et figurent dans les manuels scolaires depuis longtemps. De nombreux statisticiens travaillent sur l’apprentissage profond et sur des méthodes théoriques non classiques, tout comme les physiciens du XXe siècle avaient besoin d’élargir le cadre de la physique classique. En fait, brouiller les frontières entre informaticiens et statisticiens profite aux deux parties.
Prédiction et ajustement du modèle
Les scientifiques ont toujours comparé les résultats de calcul du modèle avec les résultats d'observation réels pour vérifier l'exactitude du modèle. L'astronome égyptien Ptolémée a proposé un ingénieux modèle du mouvement planétaire. Le modèle de Ptolémée suivait le géocentrisme mais comportait une série d'épicycles (voir l'image ci-dessous), ce qui lui confère une excellente précision prédictive. En revanche, le modèle héliocentrique original de Copernic était plus simple que le modèle ptolémaïque mais moins précis dans la prévision des observations. (Copernic a ajouté plus tard ses propres épicycles pour être comparables au modèle de Ptolémée.)
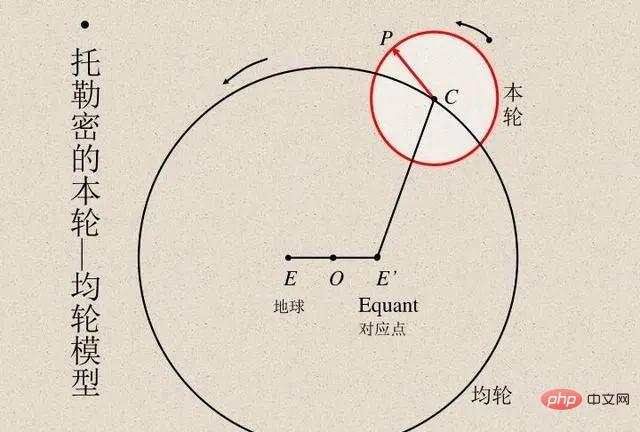
Les modèles de Ptolémée et de Copernic sont sans précédent. Si nous voulons faire des prédictions à partir d’une « boîte noire », alors le modèle géocentrique de Ptolémée est supérieur. Mais si vous voulez un modèle simple dans lequel vous pouvez « regarder à l’intérieur » (qui est le point de départ des théories expliquant le mouvement stellaire), alors le modèle de Copernic est la voie à suivre. Plus tard, Kepler a amélioré le modèle de Copernic en une orbite elliptique et a proposé les trois lois de Kepler sur le mouvement planétaire, qui ont permis à Newton d'expliquer les lois planétaires avec la loi de la gravité applicable à la Terre.
Il est donc important que le modèle héliocentrique ne soit pas simplement une « boîte noire » qui fournit des prédictions, mais soit donné par quelques équations mathématiques simples, mais avec très peu de « pièces mobiles » dans les équations. L’astronomie est depuis de nombreuses années une source d’inspiration pour le développement de techniques statistiques. Gauss et Legendre ont inventé indépendamment la régression des moindres carrés vers 1800 pour prédire les orbites des astéroïdes et autres corps célestes. En 1847, Cauchy invente la méthode de descente de gradient, également motivée par des prédictions astronomiques.
En physique, les chercheurs disposent parfois de tous les détails pour trouver la « bonne » théorie, optimiser la précision des prédictions et fournir la meilleure explication des données. Celles-ci entrent dans le cadre d'idées telles que le rasoir d'Occam, qui peuvent être considérées comme supposant que la simplicité, le pouvoir prédictif et le pouvoir explicatif sont tous en harmonie les uns avec les autres.
Cependant, dans de nombreux autres domaines, la relation entre les deux objectifs d’explication et de prédiction n’est pas aussi harmonieuse. Si vous souhaitez simplement prédire les observations, il est probablement préférable de passer par une « boîte noire ». D’un autre côté, si l’on souhaite obtenir des informations explicatives, telles que des modèles causals, des principes généraux ou des caractéristiques importantes, alors plus le modèle peut être compris et expliqué est simple, mieux c’est.
Le bon choix du modèle dépend de sa destination. Par exemple, considérons un ensemble de données contenant l'expression génétique et les phénotypes de nombreux individus (par exemple, une maladie). Si l'objectif est de prédire le risque qu'une personne tombe malade, peu importe sa complexité ou le nombre de gènes sur lesquels il repose. utiliser Le meilleur modèle prédictif adapté à la tâche. Au contraire, si l’objectif est d’identifier quelques gènes en vue d’une étude plus approfondie, alors une « boîte noire » complexe et très précise est d’une utilité limitée.
Le statisticien Leo Breiman a souligné ce point dans son célèbre article de 2001 sur Deux cultures dans la modélisation statistique. La première est une « culture de modélisation des données » qui se concentre sur des modèles génératifs simples capables d’expliquer les données. La seconde est une « culture de modélisation algorithmique » qui est agnostique quant à la manière dont les données ont été générées et se concentre sur la recherche de modèles capables de prédire les données, quelle que soit leur complexité.

Titre de l'article :
Modélisation statistique : les deux cultures
Lien de l'article :
https://projecteuclid.org/euclid.ss/1009213726
Breiman estime que les statistiques sont trop influencées par la première culture Domination , cette focalisation crée deux problèmes :
- conduit à des théories non pertinentes et à des conclusions scientifiques douteuses
- empêche les statisticiens d'étudier de nouvelles questions passionnantes
Dès que l'article de Breiman est sorti, il a suscité une certaine controverse. Son collègue statisticien Brad Efron a répondu que même s'il était d'accord avec certains points, il a également souligné que l'argument de Breiman semblait être contre la frugalité et la perspicacité scientifique en faveur d'un effort considérable pour créer des « boîtes noires » complexes. Mais dans un article récent, Efron a abandonné son point de vue précédent et a admis que Breima était plus prémonitoire parce que « les statistiques du 21e siècle se concentrent sur les algorithmes prédictifs, qui ont évolué dans une large mesure dans le sens proposé par Breiman ».
Modèles prédictifs classiques et modernes
L'apprentissage automatique, qu'il s'agisse d'apprentissage profond ou non, a évolué dans le sens de la deuxième perspective de Breiman, axée sur la prédiction. Cette culture a une longue histoire. Par exemple, le manuel de Duda et Hart publié en 1973 et l'article de Highleyman de 1962 décrivent le contenu de la figure ci-dessous, qui est très facile à comprendre pour les chercheurs en apprentissage profond d'aujourd'hui :

Duda et Hart Extraits du manuel "Classification des modèles et analyse de scène" et l'article de Highleyman de 1962 "La conception et l'analyse des expériences de reconnaissance de formes".
De même, l'image ci-dessous de l'ensemble de données de caractères manuscrits de Highleyman et de l'architecture utilisée pour l'adapter, Chow (1962) (précision ~ 58 %), trouvera un écho auprès de nombreuses personnes.

Pourquoi l'apprentissage profond est-il différent ?
En 1992, Geman, Bienenstock et Doursat ont écrit un article pessimiste sur les réseaux de neurones, affirmant que « les réseaux de neurones à action directe actuels sont largement insuffisants pour résoudre des problèmes difficiles de perception et d'apprentissage automatique ». Plus précisément, ils soutiennent que les réseaux neuronaux à usage général ne parviendront pas à gérer des tâches difficiles et que la seule manière d’y parvenir est de recourir à des fonctionnalités conçues artificiellement. Selon leurs termes : « Les propriétés importantes doivent être intégrées ou « câblées »... plutôt que apprises dans un sens statistique. » Il semble maintenant que Geman et al. se trompent complètement, mais il est plus intéressant de comprendre. pourquoi ils ont tort.
Le deep learning est en effet différent des autres méthodes d’apprentissage. Bien que l’apprentissage profond puisse ressembler à une simple prédiction, comme le plus proche voisin ou une forêt aléatoire, il peut avoir des paramètres plus complexes. Cela semble être une différence quantitative plutôt que qualitative. Mais en physique, dès que l’échelle change de quelques ordres de grandeur, une théorie complètement différente est souvent nécessaire, et il en va de même pour l’apprentissage profond. Les processus sous-jacents du deep learning et des modèles classiques (paramétriques ou non paramétriques) sont complètement différents, bien que leurs équations mathématiques (et le code Python) soient les mêmes à un niveau élevé.
Pour illustrer ce point, considérons deux scénarios différents : adapter un modèle statistique et enseigner les mathématiques aux élèves.
Scénario A : Ajustement d'un modèle statistique
Les étapes typiques pour ajuster un modèle statistique à l'aide de données sont les suivantes :
1. Voici quelques données  (
( est la matrice de
est la matrice de  ;
;  est le vecteur
est le vecteur  dimensionnel, c'est-à-dire l'étiquette de catégorie. Considérez les données comme provenant d'un modèle qui a une structure et contient du bruit, qui est le modèle à ajuster)
dimensionnel, c'est-à-dire l'étiquette de catégorie. Considérez les données comme provenant d'un modèle qui a une structure et contient du bruit, qui est le modèle à ajuster)
2. Utilisez les données ci-dessus pour ajuster un modèle et utilisez un algorithme d'optimisation pour minimiser le risque empirique. C'est-à-dire, trouvez un tel
et utilisez un algorithme d'optimisation pour minimiser le risque empirique. C'est-à-dire, trouvez un tel  via l'algorithme d'optimisation de sorte que
via l'algorithme d'optimisation de sorte que 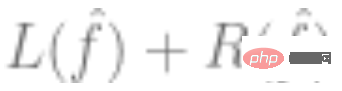 soit le plus petit,
soit le plus petit,  représente la perte (indiquant à quel point la valeur prédite est proche de la valeur vraie) et
représente la perte (indiquant à quel point la valeur prédite est proche de la valeur vraie) et  soit un terme de régularisation facultatif.
soit un terme de régularisation facultatif.
3. Plus la perte globale du modèle est faible, mieux c'est, c'est-à-dire que la valeur de l'erreur de généralisation 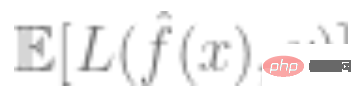 est relativement minime.
est relativement minime.
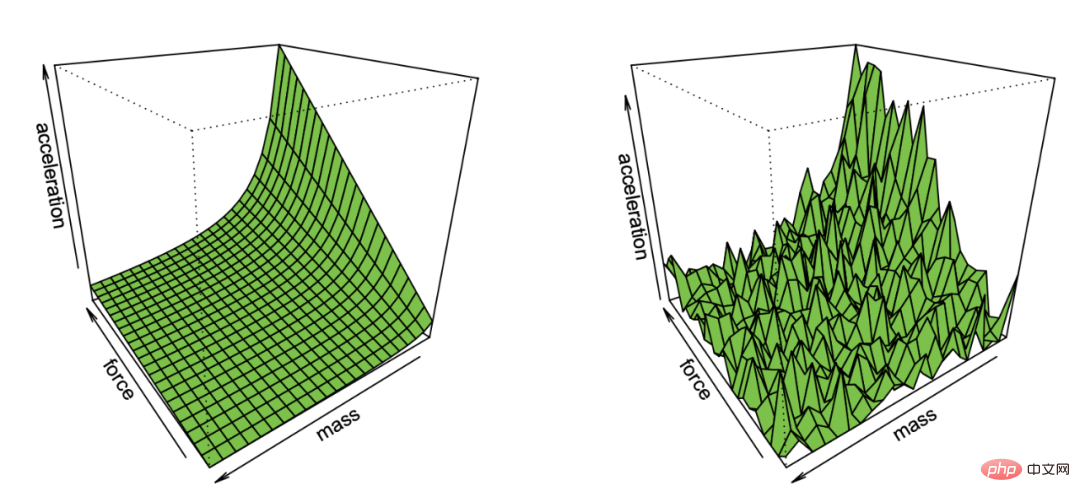
Illustration d'Effron de la récupération de la première loi de Newton à partir d'observations contenant du bruit
Cet exemple très général contient en fait de nombreux contenus, tels que la régression linéaire des moindres carrés, le voisin le plus proche, l'entraînement des réseaux de neurones, etc. Dans les scénarios statistiques classiques, nous rencontrons généralement la situation suivante :
Compromis : supposons un ensemble de modèles optimisé (si la fonction est non convexe ou contient un terme de régularisation, un algorithme et une régularisation soigneusement sélectionnés peuvent aboutir à un ensemble de Le biais de est l'approximation la plus proche de la valeur réelle qu'un élément peut atteindre. Plus l'ensemble est grand, plus le biais est petit et peut être égal à 0 (si la variance du modèle de sortie est grande. L'erreur de généralisation globale est la suivante. somme de biais et de variance. Par conséquent, l'apprentissage statistique est généralement un compromis biais-variance, et la complexité correcte du modèle consiste à minimiser l'erreur globale. Leur attitude pessimiste à l'égard des réseaux neuronaux, soutiennent-ils : Les limitations fondamentales causées par le biais. Le dilemme de la variance s'applique à tous les modèles d'inférence non paramétriques, y compris les réseaux de neurones
"Plus on est de fous, plus on est de fous" : dans l'apprentissage statistique, plus de fonctionnalités ou de données n'améliorent pas nécessairement les performances. Par exemple, il est difficile d'apprendre. à partir de données contenant de nombreuses caractéristiques non pertinentes. De même, l'apprentissage à partir d'un modèle de mélange, où les données proviennent de l'une des deux distributions (telles que et , est difficile à apprendre chaque distribution indépendamment
Rendements décroissants : dans plusieurs). Dans certains cas, le nombre de points de données requis pour réduire le bruit de prédiction au niveau est lié aux paramètres et, c'est-à-dire que le nombre de points de données est approximativement égal à. Il faut environ k échantillons pour commencer, mais une fois que vous l'avez fait, vous faites face à des rendements décroissants. , c'est-à-dire que s'il faut k points pour atteindre une précision de 90 %, il faut environ k points supplémentaires pour augmenter la précision à 95 %. De manière générale, à mesure que les ressources augmentent (qu'il s'agisse de données, de complexité du modèle ou de calcul), on espère obtenir des distinctions de plus en plus fines. , plutôt que de débloquer de nouvelles fonctionnalités spécifiques
Forte dépendance à la perte de données : lors de l'ajustement d'un modèle à des données de grande dimension, tout petit détail peut faire une grande différence dans le choix du régulariseur L1 ou L2, sans parler de l'utilisation d'un régulateur complètement nombre différent d'optimiseurs de grande dimension. Ils sont également très différents les uns des autres.
Les données sont relativement "naïves" : on suppose généralement que les données sont échantillonnées indépendamment d'une certaine distribution, bien que les points proches de la limite de décision soient difficiles. Pour classer, compte tenu du phénomène de concentration des mesures en grandes dimensions, on peut considérer que les distances de la plupart des points sont similaires. Par conséquent, dans la distribution classique des données, la différence de distance entre les points de données n'est pas grande. peut montrer cette différence, donc, contrairement aux autres problèmes mentionnés ci-dessus, cette différence est courante dans les statistiques
Scénario B : Apprendre les mathématiques
Dans ce scénario, nous supposons que vous souhaitez enseigner aux élèves les mathématiques (comme le calcul des dérivées) à travers certains. instructions et exercices. Ce scénario n'est pas formellement défini. Il existe certaines caractéristiques qualitatives :
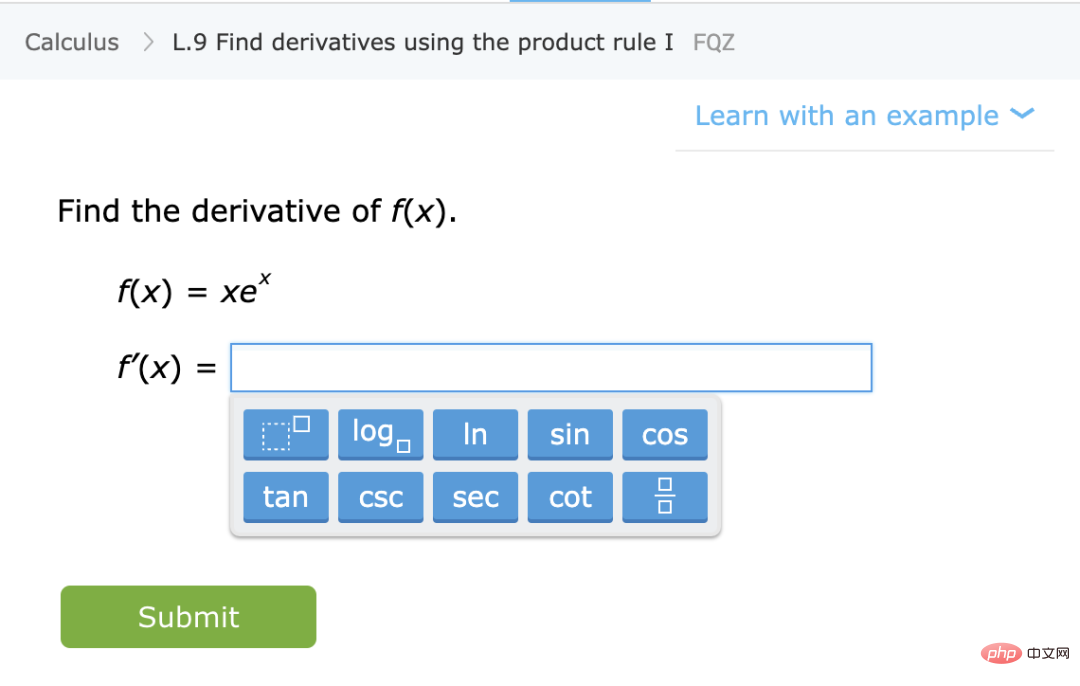 Apprendre une compétence plutôt que se rapprocher d'une distribution statistique : Dans ce cas, les élèves apprennent une compétence plutôt que l'estimation/prédiction d'une certaine distribution. quantité. , même si la fonction qui mappe les exercices aux solutions ne peut pas être utilisée comme une « boîte noire » pour résoudre certaines tâches inconnues, les schémas de pensée formés par les élèves lors de la résolution de ces problèmes sont toujours utiles pour des tâches inconnues.
Apprendre une compétence plutôt que se rapprocher d'une distribution statistique : Dans ce cas, les élèves apprennent une compétence plutôt que l'estimation/prédiction d'une certaine distribution. quantité. , même si la fonction qui mappe les exercices aux solutions ne peut pas être utilisée comme une « boîte noire » pour résoudre certaines tâches inconnues, les schémas de pensée formés par les élèves lors de la résolution de ces problèmes sont toujours utiles pour des tâches inconnues.
Plus il y en a, mieux c'est : de manière générale, les étudiants qui répondent à plus de questions et couvrent un plus large éventail de types de questions obtiennent de meilleurs résultats. Faire quelques questions de calcul et d'algèbre en même temps n'entraînera pas une baisse des résultats de calcul des élèves, mais peut les aider à améliorer leurs résultats de calcul.
De l'amélioration des capacités à la représentation automatisée : bien que la résolution de problèmes présente également des rendements décroissants dans certains cas, les élèves apprennent en plusieurs étapes. Il y a une étape où la résolution de certains problèmes permet de comprendre les concepts et de débloquer de nouvelles capacités. De plus, lorsque les élèves répètent un type spécifique de problème, ils formeront un processus automatisé de résolution de problèmes lorsqu'ils verront des problèmes similaires, passant d'une amélioration précédente des capacités à une résolution automatique de problèmes.
Performance indépendante des données et des pertes : il existe plusieurs façons d'enseigner les concepts mathématiques. Les étudiants qui étudient en utilisant des livres, des méthodes pédagogiques ou des systèmes de notation différents peuvent finir par apprendre le même contenu et avoir des capacités mathématiques similaires.
Certains problèmes sont plus difficiles : dans les exercices de mathématiques, nous constatons souvent de fortes corrélations entre la manière dont différents élèves résolvent le même problème. Il semble y avoir un niveau de difficulté inhérent à un problème et une progression naturelle de la difficulté qui convient le mieux à l'apprentissage.
L'apprentissage profond s'apparente-t-il davantage à une estimation statistique ou à des compétences d'apprentissage des étudiants ?
Parmi les deux métaphores ci-dessus, laquelle est la plus appropriée pour décrire l’apprentissage profond moderne ? Concrètement, qu’est-ce qui fait son succès ? L'ajustement du modèle statistique peut être bien exprimé à l'aide des mathématiques et du code. En fait, la boucle d'entraînement canonique de Pytorch entraîne des réseaux profonds via une minimisation empirique des risques :

À un niveau plus profond, la relation entre ces deux scénarios n'est pas claire. Pour être plus précis, voici une tâche d’apprentissage spécifique à titre d’exemple. Considérons un algorithme de classification formé à l'aide de l'approche « apprentissage auto-supervisé + détection linéaire ». La formation spécifique de l'algorithme est la suivante :
1. Supposons que les données sont une séquence, où  est un certain point de données (comme une image) et est l'étiquette.
est un certain point de données (comme une image) et est l'étiquette.
2. Obtenez d’abord le réseau neuronal profond qui représente la fonction 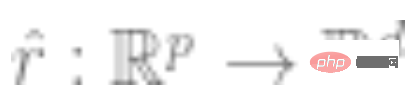 . Une fonction de perte auto-supervisée d'un certain type est formée en la minimisant en utilisant uniquement des points de données et non des étiquettes. Des exemples de telles fonctions de perte sont la reconstruction (restauration de l'entrée avec d'autres entrées) ou l'apprentissage contrastif (l'idée principale est de comparer des échantillons positifs et négatifs dans l'espace des caractéristiques pour apprendre la représentation des caractéristiques de l'échantillon).
. Une fonction de perte auto-supervisée d'un certain type est formée en la minimisant en utilisant uniquement des points de données et non des étiquettes. Des exemples de telles fonctions de perte sont la reconstruction (restauration de l'entrée avec d'autres entrées) ou l'apprentissage contrastif (l'idée principale est de comparer des échantillons positifs et négatifs dans l'espace des caractéristiques pour apprendre la représentation des caractéristiques de l'échantillon).
3. Ajustez un classificateur linéaire 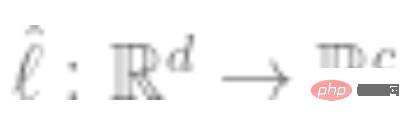 (qui est le nombre de classes) en utilisant les données étiquetées complètes pour minimiser la perte d'entropie croisée. Notre classificateur final est :
(qui est le nombre de classes) en utilisant les données étiquetées complètes pour minimiser la perte d'entropie croisée. Notre classificateur final est :
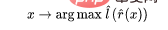
L'étape 3 ne fonctionne que pour les classificateurs linéaires, donc la « magie » se produit à l'étape 2 (apprentissage auto-supervisé des réseaux profonds). Il existe certaines propriétés importantes dans l'apprentissage auto-supervisé :
Apprendre une compétence au lieu de se rapprocher d'une fonction : l'apprentissage auto-supervisé ne consiste pas à se rapprocher d'une fonction, mais à apprendre des représentations qui peuvent être utilisées pour une variété de tâches en aval (c'est-à-dire le paradigme dominant dans le traitement du langage naturel). L'obtention de tâches en aval par sondage linéaire, réglage fin ou excitation est secondaire.
Plus on est de fous : dans l'apprentissage auto-supervisé, la qualité de la représentation s'améliore à mesure que la quantité de données augmente et ne se détériore pas en mélangeant des données provenant de plusieurs sources. En fait, plus les données sont diversifiées, mieux c’est.
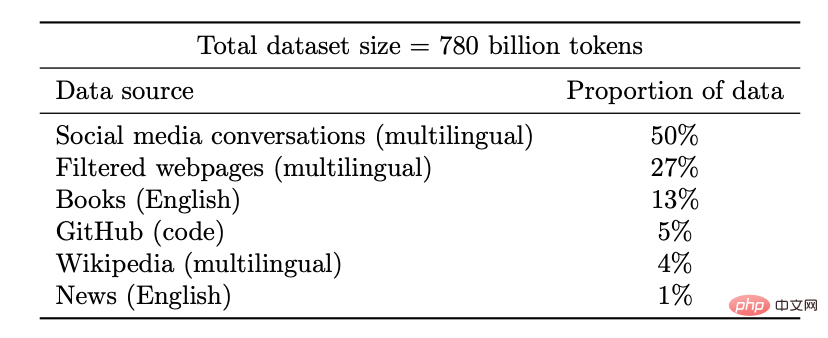
Ensemble de données du modèle Coogle PaLM
Débloquez de nouvelles capacités : à mesure que l'investissement en ressources (données, calcul, taille du modèle) augmente, les modèles d'apprentissage profond s'améliorent également de manière discontinue. Cela a également été démontré dans certains environnements combinés.
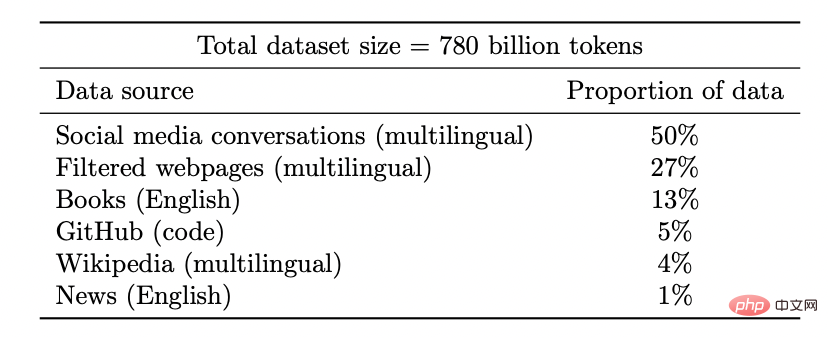
À mesure que la taille du modèle augmente, PaLM affiche des améliorations discrètes dans les benchmarks et débloque des fonctionnalités surprenantes, comme expliquer pourquoi une blague est drôle.
Les performances sont presque indépendantes de la perte ou des données : il existe de multiples pertes auto-supervisées, de multiples pertes de contraste et de reconstruction sont en fait utilisées dans la recherche d'images, les modèles de langage utilisent une reconstruction unilatérale (prédisant le prochain jeton) ou utilisant un modèle de masque, les prédictions viennent de gauche à droite L'entrée de masque du jeton. Il est également possible d'utiliser des ensembles de données légèrement différents. Ceux-ci peuvent affecter l'efficacité, mais tant que des choix « raisonnables » sont faits, la ressource d'origine améliore souvent davantage les performances de prévision que la perte spécifique ou l'ensemble de données utilisé.
Certains cas sont plus difficiles que d'autres : ce point n'est pas spécifique à l'apprentissage auto-supervisé. Les points de données semblent avoir un certain « niveau de difficulté » inhérent. En fait, différents algorithmes d'apprentissage ont différents "niveaux de compétence", et différents fichiers de données ont différents "niveaux de difficulté" (la probabilité qu'un classificateur classe correctement un point augmente de façon monotone avec la compétence et diminue de manière monotone avec la difficulté).
Le paradigme « compétence contre difficulté » est l'explication la plus claire du phénomène de « précision en jeu » découvert par Recht et al. L'article de Kaplen, Ghosh, Garg et Nakkiran montre également comment différentes entrées dans un ensemble de données ont des « profils de difficulté » inhérents qui sont généralement robustes aux différentes familles de modèles.
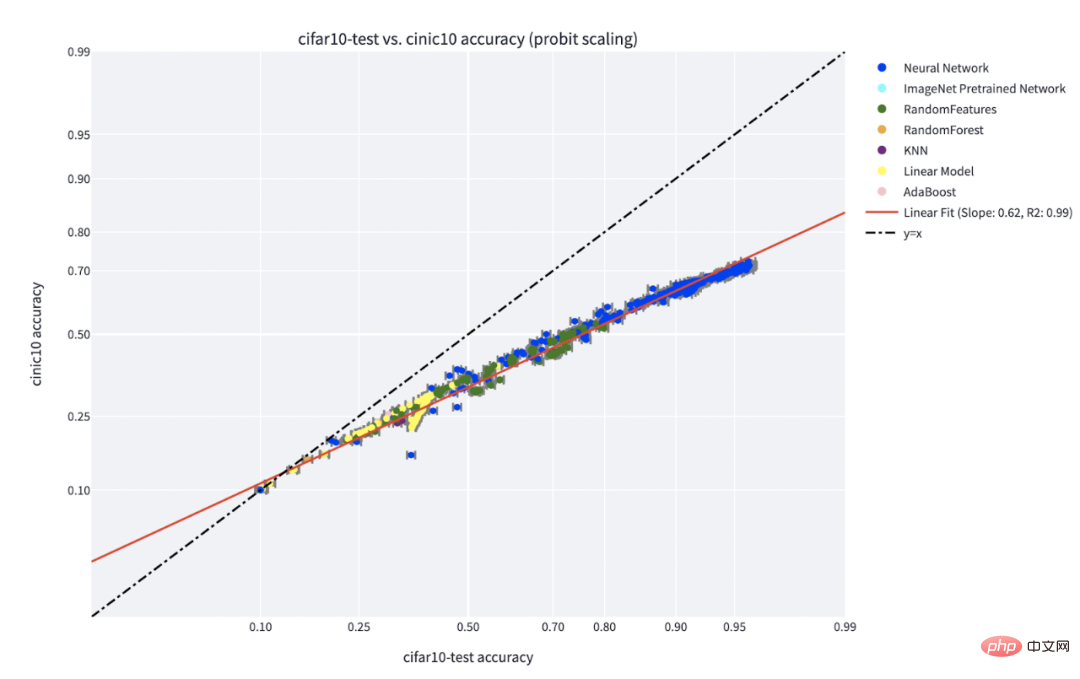
C** précision sur le phénomène de ligne pour un classificateur formé sur IFAR-10 et testé sur CINIC-10. Source de la figure : https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/
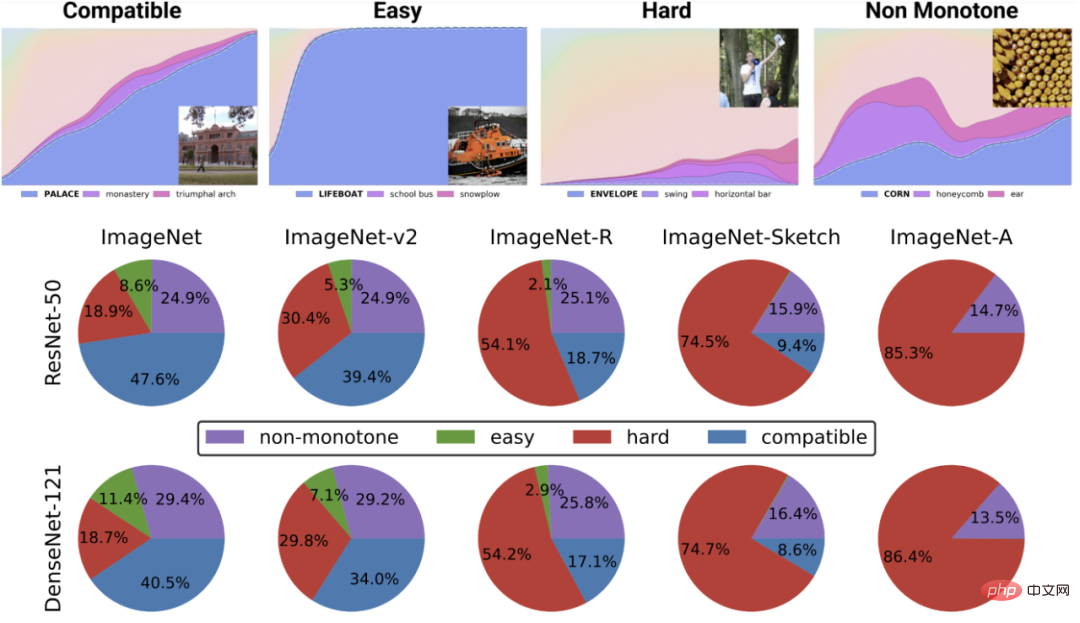
La figure du haut représente différentes probabilités softmax pour la classe la plus probable en fonction de la précision globale d'un certain classificateur de classe. , la catégorie est indexée par temps de formation. Le diagramme circulaire du bas montre la décomposition de différents ensembles de données en différents types de points (notez que cette décomposition est similaire pour différentes structures neuronales).
La formation, c'est l'enseignement : la formation de grands modèles modernes ressemble plus à un enseignement aux étudiants plutôt qu'à une adaptation du modèle aux données. Lorsque les étudiants ne comprennent pas ou se sentent fatigués, ils se "reposent" ou essaient différentes méthodes (différences de formation). Les journaux de formation des grands modèles de Meta sont instructifs : en plus des problèmes matériels, nous pouvons également voir des interventions telles que le changement d'algorithmes d'optimisation pendant la formation, et même l'envisagement de fonctions d'activation « d'échange à chaud » (GELU vers RELU). Ce dernier point n'a pas beaucoup de sens si vous considérez la formation de modèles comme un ajustement aux données plutôt que comme l'apprentissage d'une représentation.
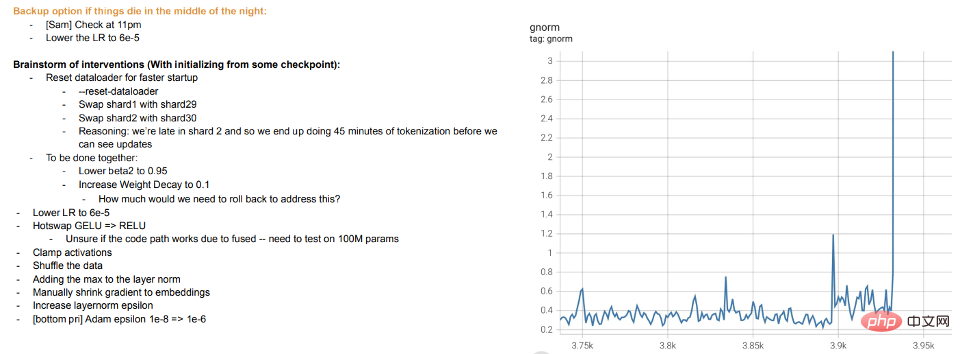
Extrait du journal de méta-entraînement
4.1 Mais qu'en est-il de l'apprentissage supervisé ?
L'apprentissage auto-supervisé a été évoqué plus tôt, mais l'exemple typique de l'apprentissage profond reste l'apprentissage supervisé. Après tout, le « moment ImageNet » du deep learning est venu d’ImageNet. Alors, ce qui a été discuté ci-dessus s’applique-t-il toujours à ce paramètre ?
Premièrement, l’émergence de l’apprentissage profond supervisé à grande échelle a été quelque peu accidentelle, grâce à la disponibilité de grands ensembles de données étiquetés de haute qualité (c’est-à-dire ImageNet). Si vous avez une bonne imagination, vous pouvez imaginer une histoire alternative dans laquelle l’apprentissage profond a commencé à faire des percées dans le traitement du langage naturel grâce à l’apprentissage non supervisé, avant de passer à la vision et à l’apprentissage supervisé.
Deuxièmement, il est prouvé que l'apprentissage supervisé et l'apprentissage auto-supervisé se comportent en réalité de la même manière « en interne » malgré l'utilisation de fonctions de perte complètement différentes. Les deux atteignent généralement les mêmes performances. Plus précisément, pour chacun, on peut combiner les k premières couches d'un modèle de profondeur d formé avec auto-supervision avec les d-k dernières couches du modèle supervisé avec peu de perte de performances.
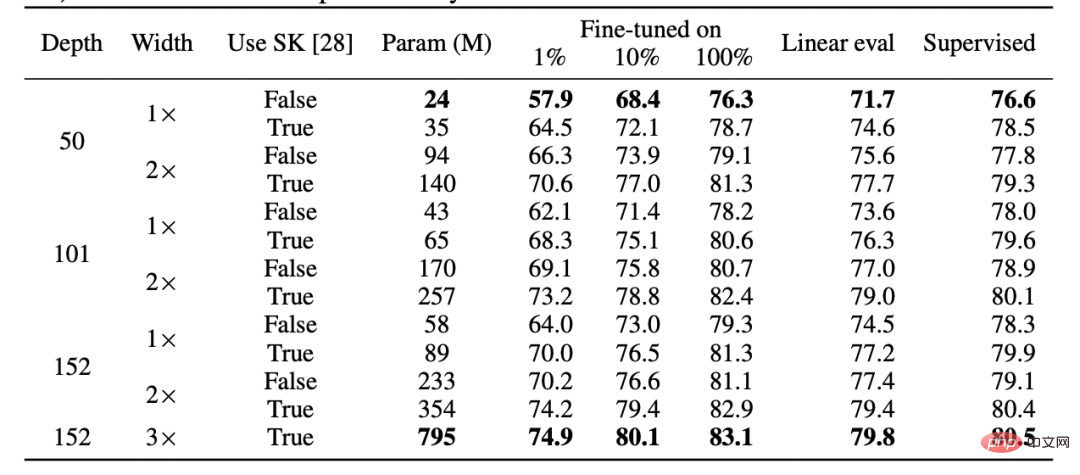
Tableau pour papier SimCLR v2. Veuillez noter la similitude générale des performances entre l'apprentissage supervisé, affiné (100%) auto-supervisé et auto-supervisé + détection linéaire (Source : https://arxiv.org/abs/2006.10029)
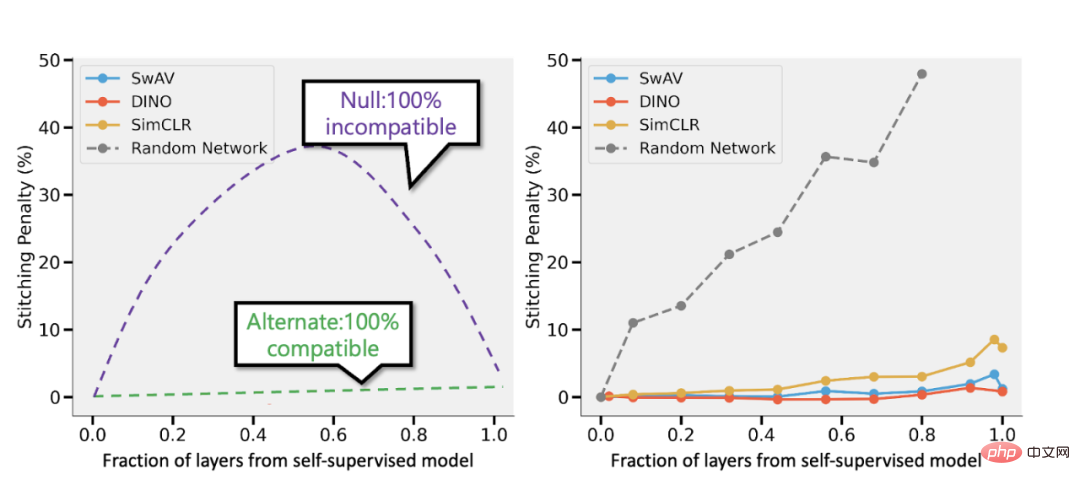
Spliced à partir du modèle supervisé et du modèle supervisé de Bansal et al. Gauche : Si la précision du modèle auto-supervisé est (disons) 3 % inférieure à celle du modèle supervisé, alors une représentation entièrement compatible entraînera une pénalité d'épissage de p 3 % lorsque p parties de la couche proviennent du modèle auto-supervisé. modèle. Si les modèles sont complètement incompatibles, nous nous attendons à ce que la précision diminue considérablement à mesure que davantage de modèles sont fusionnés. À droite : résultats réels combinant différents modèles auto-supervisés.
L'avantage des modèles simples et auto-supervisés est qu'ils peuvent combiner l'apprentissage de fonctionnalités ou la « magie de l'apprentissage profond » (effectué par une fonction de représentation profonde) avec l'ajustement de modèle statistique (effectué par un classificateur linéaire ou autre « simple » au-dessus de cette représentation) séparation.
Enfin, bien qu'il s'agisse davantage d'une spéculation, le fait est que le « méta-apprentissage » semble souvent assimilé aux représentations d'apprentissage (voir : https://arxiv.org/abs/1909.09157, https://arxiv. org/abs /2206.03271), ce qui peut être considéré comme une autre preuve que cela se fait en grande partie quels que soient les objectifs de l'optimisation du modèle.
4.2 Que faire en cas de surparamétrage ?
Cet article ignore ce qui est considéré comme des exemples classiques de différences entre les modèles d'apprentissage statistique et l'apprentissage profond dans la pratique : l'absence de « compromis biais-variance » et la capacité des modèles surparamétrés à bien généraliser.
Pourquoi sauter ? Il y a deux raisons :
- Tout d’abord, si l’apprentissage supervisé est effectivement égal à l’apprentissage auto-supervisé + simple, alors cela peut expliquer sa capacité de généralisation.
- Deuxièmement, la sur-paramétrisation n'est pas la clé du succès du deep learning. Ce qui rend les réseaux profonds spéciaux, ce n’est pas qu’ils soient grands par rapport au nombre d’échantillons, mais qu’ils soient grands en termes absolus. En fait, généralement dans l’apprentissage non supervisé/auto-supervisé, le modèle n’est pas surparamétré. Même pour les très grands modèles de langage, leurs ensembles de données sont plus volumineux.

L'article "deep bootstrap" de Nakkiran-Neyshabur-Sadghi montre que les architectures modernes se comportent de la même manière dans le régime "surparamétré" ou "sous-échantillonné" (le modèle est formé sur des données limitées pendant de nombreuses époques jusqu'à ce qu'il surajustements : "Monde réel" dans la figure ci-dessus), il en va de même dans l'état "sous-paramétré" ou "en ligne" (le modèle est entraîné pour une seule époque, et chaque échantillon n'est visualisé qu'une seule fois : "Monde idéal" dans la figure ci-dessus). Source de l'image : https://arxiv.org/abs/2010.08127
Summary
L'apprentissage statistique joue certainement un rôle dans l'apprentissage profond. Cependant, malgré l’utilisation d’une terminologie et d’un code similaires, considérer l’apprentissage profond comme un simple ajustement d’un modèle avec plus de paramètres qu’un modèle classique passe à côté de nombreux éléments essentiels à son succès. La métaphore pour enseigner les mathématiques aux élèves n’est pas non plus parfaite.
Comme l'évolution biologique, bien que l'apprentissage profond contienne de nombreuses règles réutilisées (comme la descente de gradient avec perte d'expérience), il peut produire des résultats très complexes. Il semble qu'à différents moments, différents composants du réseau apprennent différentes choses, notamment l'apprentissage des représentations, l'ajustement prédictif, la régularisation implicite et le bruit pur. Les chercheurs sont toujours à la recherche du bon angle pour poser des questions sur l’apprentissage profond, et encore moins pour y répondre.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Ce site a rapporté le 27 juin que Jianying est un logiciel de montage vidéo développé par FaceMeng Technology, une filiale de ByteDance. Il s'appuie sur la plateforme Douyin et produit essentiellement du contenu vidéo court pour les utilisateurs de la plateforme. Il est compatible avec iOS, Android et. Windows, MacOS et autres systèmes d'exploitation. Jianying a officiellement annoncé la mise à niveau de son système d'adhésion et a lancé un nouveau SVIP, qui comprend une variété de technologies noires d'IA, telles que la traduction intelligente, la mise en évidence intelligente, l'emballage intelligent, la synthèse humaine numérique, etc. En termes de prix, les frais mensuels pour le clipping SVIP sont de 79 yuans, les frais annuels sont de 599 yuans (attention sur ce site : équivalent à 49,9 yuans par mois), l'abonnement mensuel continu est de 59 yuans par mois et l'abonnement annuel continu est de 59 yuans par mois. est de 499 yuans par an (équivalent à 41,6 yuans par mois) . En outre, le responsable de Cut a également déclaré que afin d'améliorer l'expérience utilisateur, ceux qui se sont abonnés au VIP d'origine
 Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
Améliorez la productivité, l’efficacité et la précision des développeurs en intégrant une génération et une mémoire sémantique améliorées par la récupération dans les assistants de codage IA. Traduit de EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, auteur JanakiramMSV. Bien que les assistants de programmation d'IA de base soient naturellement utiles, ils ne parviennent souvent pas à fournir les suggestions de code les plus pertinentes et les plus correctes, car ils s'appuient sur une compréhension générale du langage logiciel et des modèles d'écriture de logiciels les plus courants. Le code généré par ces assistants de codage est adapté à la résolution des problèmes qu’ils sont chargés de résoudre, mais n’est souvent pas conforme aux normes, conventions et styles de codage des équipes individuelles. Cela aboutit souvent à des suggestions qui doivent être modifiées ou affinées pour que le code soit accepté dans l'application.
 Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Les grands modèles linguistiques (LLM) sont formés sur d'énormes bases de données textuelles, où ils acquièrent de grandes quantités de connaissances du monde réel. Ces connaissances sont intégrées à leurs paramètres et peuvent ensuite être utilisées en cas de besoin. La connaissance de ces modèles est « réifiée » en fin de formation. À la fin de la pré-formation, le modèle arrête effectivement d’apprendre. Alignez ou affinez le modèle pour apprendre à exploiter ces connaissances et répondre plus naturellement aux questions des utilisateurs. Mais parfois, la connaissance du modèle ne suffit pas, et bien que le modèle puisse accéder à du contenu externe via RAG, il est considéré comme bénéfique de l'adapter à de nouveaux domaines grâce à un réglage fin. Ce réglage fin est effectué à l'aide de la contribution d'annotateurs humains ou d'autres créations LLM, où le modèle rencontre des connaissances supplémentaires du monde réel et les intègre.
 Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Pour en savoir plus sur l'AIGC, veuillez visiter : 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou est différent de la banque de questions traditionnelle que l'on peut voir partout sur Internet. nécessite de sortir des sentiers battus. Les grands modèles linguistiques (LLM) sont de plus en plus importants dans les domaines de la science des données, de l'intelligence artificielle générative (GenAI) et de l'intelligence artificielle. Ces algorithmes complexes améliorent les compétences humaines et stimulent l’efficacité et l’innovation dans de nombreux secteurs, devenant ainsi la clé permettant aux entreprises de rester compétitives. LLM a un large éventail d'applications. Il peut être utilisé dans des domaines tels que le traitement du langage naturel, la génération de texte, la reconnaissance vocale et les systèmes de recommandation. En apprenant de grandes quantités de données, LLM est capable de générer du texte
 Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
 Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
L'ensemble de données ScienceAI Question Answering (QA) joue un rôle essentiel dans la promotion de la recherche sur le traitement du langage naturel (NLP). Des ensembles de données d'assurance qualité de haute qualité peuvent non seulement être utilisés pour affiner les modèles, mais également évaluer efficacement les capacités des grands modèles linguistiques (LLM), en particulier la capacité à comprendre et à raisonner sur les connaissances scientifiques. Bien qu’il existe actuellement de nombreux ensembles de données scientifiques d’assurance qualité couvrant la médecine, la chimie, la biologie et d’autres domaines, ces ensembles de données présentent encore certaines lacunes. Premièrement, le formulaire de données est relativement simple, et la plupart sont des questions à choix multiples. Elles sont faciles à évaluer, mais limitent la plage de sélection des réponses du modèle et ne peuvent pas tester pleinement la capacité du modèle à répondre aux questions scientifiques. En revanche, les questions et réponses ouvertes
 AlphaFold 3 est lancé, prédisant de manière exhaustive les interactions et les structures des protéines et de toutes les molécules de la vie, avec une précision bien plus grande que jamais
Jul 16, 2024 am 12:08 AM
AlphaFold 3 est lancé, prédisant de manière exhaustive les interactions et les structures des protéines et de toutes les molécules de la vie, avec une précision bien plus grande que jamais
Jul 16, 2024 am 12:08 AM
Editeur | Radis Skin Depuis la sortie du puissant AlphaFold2 en 2021, les scientifiques utilisent des modèles de prédiction de la structure des protéines pour cartographier diverses structures protéiques dans les cellules, découvrir des médicaments et dresser une « carte cosmique » de chaque interaction protéique connue. Tout à l'heure, Google DeepMind a publié le modèle AlphaFold3, capable d'effectuer des prédictions de structure conjointe pour des complexes comprenant des protéines, des acides nucléiques, de petites molécules, des ions et des résidus modifiés. La précision d’AlphaFold3 a été considérablement améliorée par rapport à de nombreux outils dédiés dans le passé (interaction protéine-ligand, interaction protéine-acide nucléique, prédiction anticorps-antigène). Cela montre qu’au sein d’un cadre unique et unifié d’apprentissage profond, il est possible de réaliser
 Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
Editeur | KX Dans le domaine de la recherche et du développement de médicaments, il est crucial de prédire avec précision et efficacité l'affinité de liaison des protéines et des ligands pour le criblage et l'optimisation des médicaments. Cependant, les études actuelles ne prennent pas en compte le rôle important des informations sur la surface moléculaire dans les interactions protéine-ligand. Sur cette base, des chercheurs de l'Université de Xiamen ont proposé un nouveau cadre d'extraction de caractéristiques multimodales (MFE), qui combine pour la première fois des informations sur la surface des protéines, la structure et la séquence 3D, et utilise un mécanisme d'attention croisée pour comparer différentes modalités. alignement. Les résultats expérimentaux démontrent que cette méthode atteint des performances de pointe dans la prédiction des affinités de liaison protéine-ligand. De plus, les études d’ablation démontrent l’efficacité et la nécessité des informations sur la surface des protéines et de l’alignement des caractéristiques multimodales dans ce cadre. Les recherches connexes commencent par "S





