Comment implémenter un tri simple en Java
Le tri est une opération très courante et essentielle dans le traitement des données. Bien que dans le développement réel d'un projet, il y ait une petite chance que nous devions l'implémenter manuellement. Après tout, il existe plusieurs implémentations d'algorithmes de tri dans chaque langage. bibliothèque de classe. Mais il nous est toujours très utile de comprendre ces idées subtiles. Cet article passe brièvement en revue les trois types d’algorithmes les plus élémentaires : la sélection, le bullage et l’insertion.
Définissez d'abord une fonction pour échanger des éléments de tableau, qui peut être appelée lors du tri
/**
* 交换数组元素
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a,int b){
arr[a] = arr[a]+arr[b];
arr[b] = arr[a]-arr[b];
arr[a] = arr[a]-arr[b];
}Tri par sélection simple
Le tri par sélection simple est l'algorithme le plus simple et le plus intuitif. L'idée de base est de sélectionner la plus petite valeur parmi les éléments de données. être trié à chaque passe (ou le plus grand) l'élément est utilisé comme premier élément jusqu'à ce que tous les éléments soient triés. Le tri par sélection simple est un tri instable.
Lorsque l'algorithme est mis en œuvre, chaque fois que l'élément minimum est déterminé, la première position sera le minimum actuel grâce à une comparaison et un échange constants. L'échange est une opération relativement longue. En fait, on peut facilement constater que ces échanges n’ont aucun sens avant que l’élément minimum actuel ne soit complètement déterminé. Nous pouvons définir une variable min pour stocker uniquement l'indice du tableau du plus petit élément pour chaque comparaison. Lorsque la boucle se termine, cette variable stocke l'indice du plus petit élément actuel, puis effectue l'opération d'échange. L’implémentation du code est très simple, jetons un coup d’œil.
Implémentation du code
/**
* 简单选择排序
*
* @param arr
*/
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;//每一趟循环比较时,min用于存放较小元素的数组下标,这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标,避免每次遇到较小元素都要进行交换。
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//进行交换,如果min发生变化,则进行交换
if (min != i) {
swap(arr,min,i);
}
}
}Après l'optimisation du tri par sélection simple ci-dessus, le nombre de comparaisons reste inchangé quelle que soit la disposition originale du tableau pour les opérations d'échange, dans le meilleur des cas, lorsque le tableau est complètement ordonné, aucun mouvement d'échange n'est effectué ; requis , dans le pire des cas, c'est-à-dire lorsque le tableau est dans l'ordre inverse, le nombre d'échanges est n-1. Pour résumer, la complexité temporelle est O(n2)
Tri à bulles
L'idée de base du tri à bulles est de comparer les éléments adjacents par paires et de les échanger dans l'ordre inverse, de cette façon, chaque passe obtiendra le plus petit. Ou le plus grand élément "flotte" vers le haut et atteint finalement l'ordre complet

Mise en œuvre du code
Dans le processus de tri des bulles, si une certaine passe est terminée sans aucune opération d'échange, comme le tableau [5 ,4 ,1,2,3], après avoir exécuté deux bullages, c'est-à-dire après deux boucles extérieures, 5 et 4 sont ajustés respectivement à la position finale [1,2,3,4,5]. À l'heure actuelle, après l'exécution de la troisième boucle, aucun échange n'a été effectué, ce qui signifie que les séquences restantes sont déjà en ordre et que l'opération de tri peut être terminée. Jetons un coup d'œil au code
/**
* 冒泡排序
*
* @param arr
*/
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;//设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已然完成。
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr,j,j+1);
flag = false;
}
}
if (flag) {
break;
}
}
}Selon le. au-dessus du risque Implémentation de la bulle, si le tableau d'origine lui-même est ordonné (c'est le meilleur des cas), seules n-1 comparaisons peuvent être effectuées s'il est dans l'ordre inverse, le nombre de comparaisons est n-1+n-2+ ; ..+1=n (n-1)/2, le nombre d'échanges et le nombre de comparaisons sont égaux. Par conséquent, sa complexité temporelle est toujours O(n2). Dans l’ensemble, les performances du tri à bulles sont encore légèrement pires que celles du tri par sélection ci-dessus.
Tri par insertion directe
L'idée de base du tri par insertion directe est d'insérer un enregistrement à trier dans la séquence ordonnée précédemment triée à chaque étape jusqu'à ce que tous les éléments soient insérés.
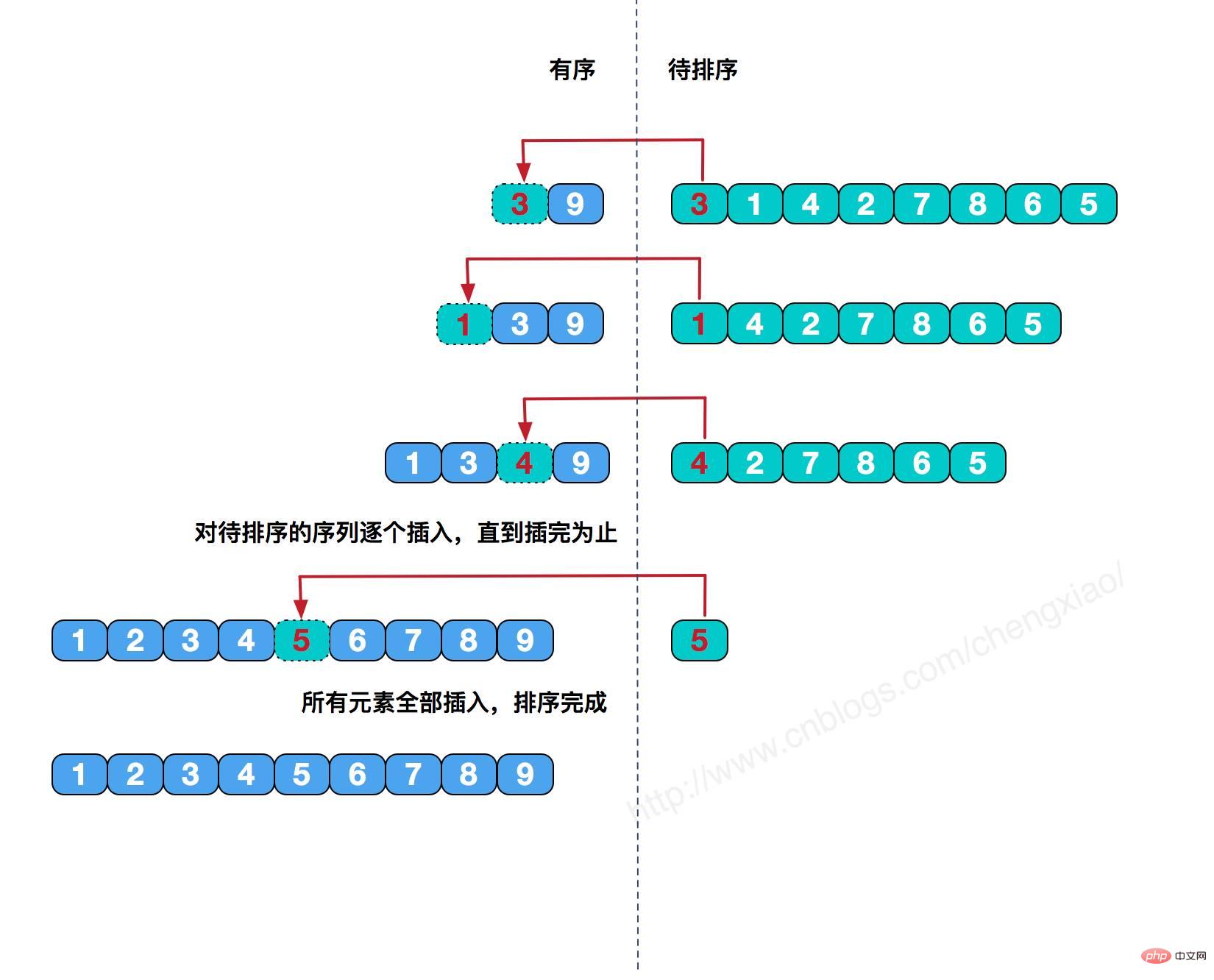
Implémentation du code
/**
* 插入排序
*
* @param arr
*/
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int j = i;
while (j > 0 && arr[j] < arr[j - 1]) {
swap(arr,j,j-1);
j--;
}
}
}Tri par insertion simple Dans le meilleur des cas, il doit être comparé n-1 fois sans échanger d'éléments, et la complexité temporelle est O(n) ; toujours O(n2). Mais lorsque les éléments du tableau sont disposés de manière aléatoire, le tri par insertion est toujours meilleur que les deux tris ci-dessus.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre parfait en Java. Nous discutons ici de la définition, comment vérifier le nombre parfait en Java ?, des exemples d'implémentation de code.
 Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Guide du générateur de nombres aléatoires en Java. Nous discutons ici des fonctions en Java avec des exemples et de deux générateurs différents avec d'autres exemples.
 Weka en Java
Aug 30, 2024 pm 04:28 PM
Weka en Java
Aug 30, 2024 pm 04:28 PM
Guide de Weka en Java. Nous discutons ici de l'introduction, de la façon d'utiliser Weka Java, du type de plate-forme et des avantages avec des exemples.
 Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre de Smith en Java. Nous discutons ici de la définition, comment vérifier le numéro Smith en Java ? exemple avec implémentation de code.
 Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Dans cet article, nous avons conservé les questions d'entretien Java Spring les plus posées avec leurs réponses détaillées. Pour que vous puissiez réussir l'interview.
 Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Java 8 présente l'API Stream, fournissant un moyen puissant et expressif de traiter les collections de données. Cependant, une question courante lors de l'utilisation du flux est: comment se casser ou revenir d'une opération FOREAK? Les boucles traditionnelles permettent une interruption ou un retour précoce, mais la méthode Foreach de Stream ne prend pas directement en charge cette méthode. Cet article expliquera les raisons et explorera des méthodes alternatives pour la mise en œuvre de terminaison prématurée dans les systèmes de traitement de flux. Lire plus approfondie: Améliorations de l'API Java Stream Comprendre le flux Forach La méthode foreach est une opération terminale qui effectue une opération sur chaque élément du flux. Son intention de conception est
 Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Guide de TimeStamp to Date en Java. Ici, nous discutons également de l'introduction et de la façon de convertir l'horodatage en date en Java avec des exemples.
 Programme Java pour trouver le volume de la capsule
Feb 07, 2025 am 11:37 AM
Programme Java pour trouver le volume de la capsule
Feb 07, 2025 am 11:37 AM
Les capsules sont des figures géométriques tridimensionnelles, composées d'un cylindre et d'un hémisphère aux deux extrémités. Le volume de la capsule peut être calculé en ajoutant le volume du cylindre et le volume de l'hémisphère aux deux extrémités. Ce tutoriel discutera de la façon de calculer le volume d'une capsule donnée en Java en utilisant différentes méthodes. Formule de volume de capsule La formule du volume de la capsule est la suivante: Volume de capsule = volume cylindrique volume de deux hémisphères volume dans, R: Le rayon de l'hémisphère. H: La hauteur du cylindre (à l'exclusion de l'hémisphère). Exemple 1 entrer Rayon = 5 unités Hauteur = 10 unités Sortir Volume = 1570,8 unités cubes expliquer Calculer le volume à l'aide de la formule: Volume = π × r2 × h (4






