 Java
Java
 javaDidacticiel
javaDidacticiel
 Comment personnaliser un tableau d'encapsulation de classe en Java pour implémenter l'opération de données
Comment personnaliser un tableau d'encapsulation de classe en Java pour implémenter l'opération de données
Comment personnaliser un tableau d'encapsulation de classe en Java pour implémenter l'opération de données
En tant que structure de stockage de données de base, les tableaux sont largement utilisés. Un tableau est une structure de données qui utilise un espace mémoire continu pour stocker une longueur fixe et le même type de données. La structure des données est indépendante du langage. Ici, Java est utilisé pour effectuer des opérations liées aux tableaux. Les index des tableaux commencent à 0.
1 Initialisation du tableau
Il existe deux façons de créer des données. L'une consiste à déclarer une longueur fixe de données, puis à attribuer une valeur au tableau, et l'autre consiste à attribuer une valeur directement.
Type 1 :
数据类型[] 数组名称 = new 数据类型[长度];
La marque [] déclare ici un tableau En plus d'être placé après le type de données, ce [] peut également être placé après le nom du tableau, avec le même effet. Si je déclare un tableau de type long d'une longueur de 2, et que j'attribue la valeur : 2的long类型的数组,并赋值:
long[] arr = new long[2]; arr[0] = 1; arr[1] = 2;
第二种:
数据类型[] 数组名称 = {元素1,元素2, ...};这样在数组初始化的时候直接给数组赋值,数组的长度由元素的个数决定。
二 自定义类封装数组实现数据操作
public class MyArray {
// 自定义数组 private long[] arr;
// 有效数据长度 private int element;
public MyArray(){
arr = new long[9];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
/**
* 显示数组元素
*/ public void display(){
System.out.print("[");
for (int i = 0; i < element; i++) {
System.out.print(arr[i]+" ");
}
System.out.print("]");
}
}2.1 添加元素
数组是用连续的内存空间来存储数据的,则每次添加的时候会往当前数组的最后一个元素上添加元素,一次就可以加上元素,所以它的复杂度为O(1),假如定义一个长度为9数组,数组中已经有两个元素,则添加第三个元素如下:
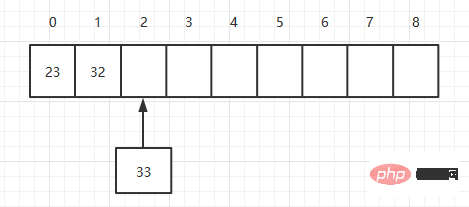
public void add(long value){
arr[element] = value;
element++;
}2.2 根据值查询元素位置
这种查找方式也叫做线性查找,就是根据传入的值循环去遍历元素,来获取对应的位置,理论上平均查询一个元素需要花费N/2次,所以它的复杂度为O(N)。
public int find(long value){
int i;
for (i = 0; i < element; i++) {
if(value == arr[i]){
break;
}
}
if(i == element){
return -1;
}else {
return i;
}
}2.3 根据索引查询元素
根据索引来查找元素,也就是获取对应位置的元素,其复杂度为O(1)。
public long get(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
return arr[index];
}
}2.4 根据索引删除元素
删除对应索引的元素后,我们需要将所有改索引后面的元素,向前移动一位。假如我要删除索引为2的元素,如下:
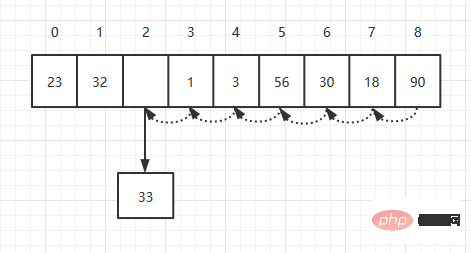
理论上平均删除一个元素,我们需要移动N/2次,所以它的时间复杂度也为O(N)。
public void delete(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
for (int i = index; i < element; i++) {
arr[index] = arr[index+1];
}
element --;
}
}2.5 修改元素
修改某个位置的元素,直接根据索引就一次就可以修改对应的元素,所以它的时间复杂度为O(1)。
public void change(int index,long newValue){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
arr[index] = newValue;
}
}三 有序数组
有序数组是数组的一种特殊类型,有序数组中的元素按照某种顺序进行排列。
3.1 添加元素
在添加元素的时候,将元素按顺序添加到某个位置。如下,在一个数组中添加一个33的元素。
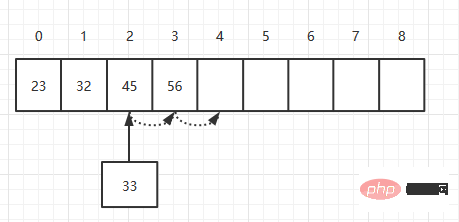
首先,将索引为3的元素移动到索引为4的位置,然后将索引为2的元素移动到索引为3的位置,最后将33添加到索引为2的位置。理论上插入一个元素需要移动元素的个数为N/2个,所以它的时间复杂度为O(N)。
public void add(long value){
int i;
for (i = 0; i < element; i++) {
if(arr[i]>value){
break;
}
}
for (int j = element; j > i; j--){
arr[j] = arr[j-1];
}
arr[i] = value;
element++;
}3.2 二分法根据元素查询索引
在无序数组中,使用线性法进行查找相关元素,线性法即按索引按个查找。有序数组可以使用二分法来查找元素,二分法是指将一个数组从中间分成两个,判断元素位于哪个数组中,然后重复这样的操作。
假如有8
public int search(long value){
// 中间值 int middle = 0;
// 最小值 int low = 0;
// 最大值 int pow = element;
while (true){
middle = (low + pow) / 2;
if(arr[middle] == value){
return middle;
}else if (low > pow){
return -1;
}else{
if(arr[middle] > value){
pow = middle - 1;
}else{
low = middle + 1;
}
}
}
}Le deuxième type
:rrreee
De cette façon, quand le tableau est initialisé, il reçoit directement l'affectation du tableau, la longueur du tableau est déterminée par le nombre d'éléments.| 2.1 Ajouter des éléments | Les tableaux utilisent un espace mémoire continu pour stocker des données, donc chaque fois que vous ajoutez un élément, un élément sera ajouté au dernier élément du tableau actuel, une fois Vous pouvez ajouter des éléments, donc sa complexité est O(1). Si vous définissez un tableau d'une longueur de 9 et qu'il y a déjà deux éléments dans le tableau, ajoutez un troisième élément comme suit : | .
|---|---|
| Cette méthode de recherche est également appelée la recherche linéaire, qui consiste à parcourir les éléments en fonction de la valeur entrante pour obtenir la position correspondante. En théorie, il faut N/2 fois pour interroger un élément en moyenne, sa complexité est donc O(N). | rrreee2.3 Interroger des éléments basés sur l'index |
| 2.4 Supprimer des éléments en fonction de l'index | Après avoir supprimé l'élément correspondant à l'index, nous devons déplacer tous les éléments après l'index modifié vers l'avant d'une position. Si je veux supprimer l'élément d'index 2, comme suit : |
| Théoriquement moyenne Pour supprimer un élément, nous devons nous déplacer N/2 fois, donc sa complexité temporelle est également O(N). | rrreee2.5 Modifier des éléments |
| Trois tableaux ordonnés | Le tableau ordonné est un type spécial de tableau. Les éléments du tableau ordonné sont disposés dans un certain ordre. |
Lors de l'ajout d'éléments, ajoutez des éléments à une certaine position dans l'ordre. Comme suit, ajoutez un élément de 33 à un tableau. |
 |
| 3.2 Méthode dichotomique pour interroger l'index en fonction des éléments | Dans un tableau non ordonné, utilisez la méthode linéaire pour trouver les éléments liés. La méthode linéaire consiste à rechercher un par un en fonction de l'index. Les tableaux triés peuvent utiliser la méthode de dichotomie pour rechercher des éléments. La dichotomie signifie diviser un tableau en deux à partir du milieu, déterminer dans quel tableau se trouve l'élément, puis répéter cette opération. |
- Plus la complexité est faible, meilleur est l'algorithme, donc O(1) > O(logN) >
Algorithme
Complexité
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Guide de la racine carrée en Java. Nous discutons ici du fonctionnement de Square Root en Java avec un exemple et son implémentation de code respectivement.
 Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre parfait en Java. Nous discutons ici de la définition, comment vérifier le nombre parfait en Java ?, des exemples d'implémentation de code.
 Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Guide du générateur de nombres aléatoires en Java. Nous discutons ici des fonctions en Java avec des exemples et de deux générateurs différents avec d'autres exemples.
 Weka en Java
Aug 30, 2024 pm 04:28 PM
Weka en Java
Aug 30, 2024 pm 04:28 PM
Guide de Weka en Java. Nous discutons ici de l'introduction, de la façon d'utiliser Weka Java, du type de plate-forme et des avantages avec des exemples.
 Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre de Smith en Java. Nous discutons ici de la définition, comment vérifier le numéro Smith en Java ? exemple avec implémentation de code.
 Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Dans cet article, nous avons conservé les questions d'entretien Java Spring les plus posées avec leurs réponses détaillées. Pour que vous puissiez réussir l'interview.
 Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Java 8 présente l'API Stream, fournissant un moyen puissant et expressif de traiter les collections de données. Cependant, une question courante lors de l'utilisation du flux est: comment se casser ou revenir d'une opération FOREAK? Les boucles traditionnelles permettent une interruption ou un retour précoce, mais la méthode Foreach de Stream ne prend pas directement en charge cette méthode. Cet article expliquera les raisons et explorera des méthodes alternatives pour la mise en œuvre de terminaison prématurée dans les systèmes de traitement de flux. Lire plus approfondie: Améliorations de l'API Java Stream Comprendre le flux Forach La méthode foreach est une opération terminale qui effectue une opération sur chaque élément du flux. Son intention de conception est
 Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Guide de TimeStamp to Date en Java. Ici, nous discutons également de l'introduction et de la façon de convertir l'horodatage en date en Java avec des exemples.





