Comment implémenter l'angle de conversion arctan en Python

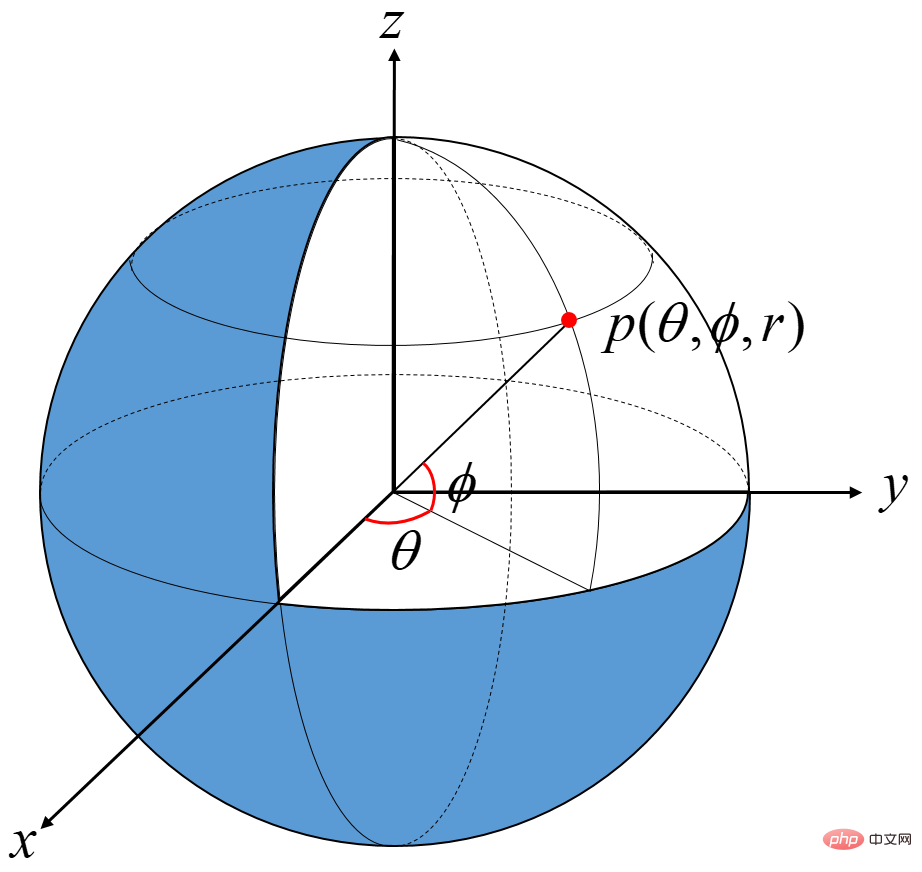
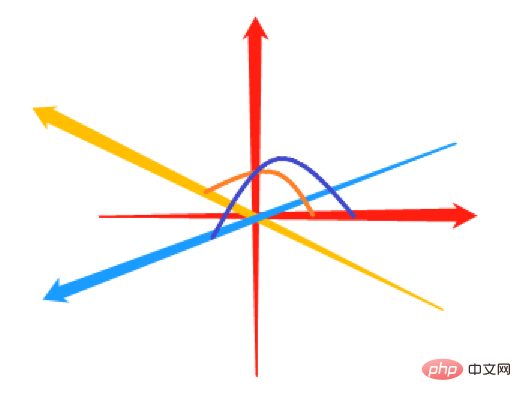
Système de coordonnées cartésiennes

Pour le système de coordonnées planes, la plage de l'angle θ entre n'importe quel rayon OP et l'axe x peut être [0,2π) ou (-π,&pi ;] , sauf indication contraire, nous utilisons ce dernier
pour exprimer le point Pc = (x, y, z) dans le système de coordonnées spatiales cartésiennes sous la forme du système de coordonnées sphériquesPs = ( θ , ϕ , r ) θ的范围，可以取[0,2π)或者(-π,π]，如无特殊说明， 我们统一使用后者。
将笛卡尔空间坐标系中的点 Pc = ( x , y , z ) 表示成球体坐标系中的形式 Ps = ( θ , ϕ , r )。

其中

根据球坐标的定义，要求θ∈[−π,π]，ϕ∈[−π/2,π/2] ，r∈[0 , +∞)。

对于 θ，正切函数的周期是 π，因此反正切函数 arctan 一般也只取一个周期，其定义域是 R，值域是(−π/2 , π/2) 。为了解决这个问题，引入了 Arctan 函数，也就是 arctan2 函数。

atan2 函数的使用 atan2(delta_y , delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan 函数的使用 atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan 和 atan2 的异同

• 参数的个数不同

• 两者返回值都是弧度

• 如果 delta_x等于0，atan2依然可以计算，但是 atan 则需要提前判断，否则就会导致程序出错

• 象限的处理

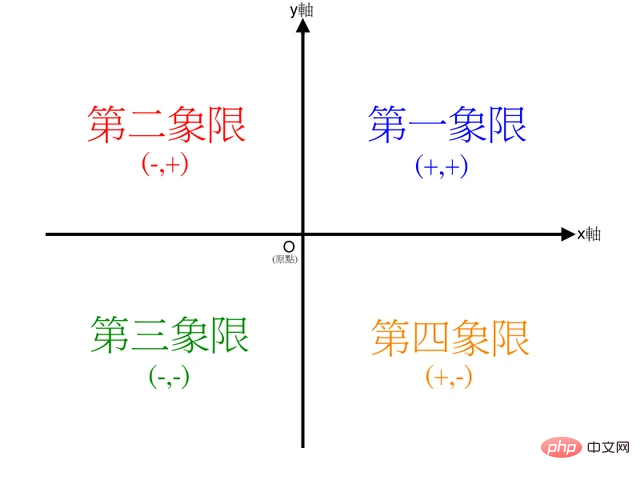
atan2(b,a)是4象限反正切，它的取值不仅取决于正切值b/a，还取决于点(b,a) 落入哪个象限：

• 当点 (b,a) 落入第一象限(b>0, a>0)时，atan2(b,a)的范围是 0 ~ pi/2

• 当点 (b,a)落入第二象限(b>0, a<0)时，atan2(b,a)的范围是 pi/2 ~ pi

• 当点 (b,a)落入第三象限(b<0, a<0)时，atan2(b,a)的范围是 -pi～-pi/2

• 当点 (b,a) 落入第四象限(b<0, a>0)时，atan2(b,a)的范围是 -pi/2～０

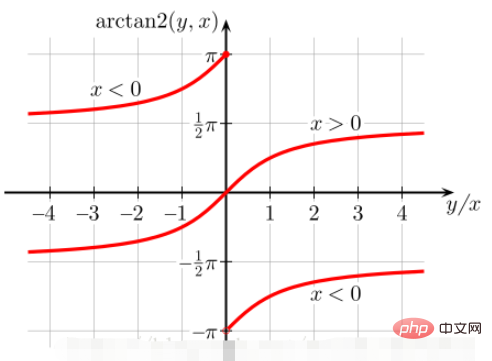
而 atan(b/a) 仅仅根据正切值为a/b求出对应的角度 (可以看作仅仅是2象限反正切)：

• 当 b/a > 0 时，atan(b/a)取值范围是 0 ~ pi/2

• 当 b/a < 0 时，atan(b/a)取值范围是 -pi/2～0

取值范围

• 点 (b,a) 落入第一象限 (b>0, a>0)或 <code>第四象限(b<0, a>0)时，atan2(b,a) = atan(b/a)

• 点 (b,a) 落入第二象限 (b>0, a<0)，b/a<0，故atan(b/a)取值范围始终是 -pi/2～０，然而，atan2(b,a)的范围是 pi/2 ~ pi，故atan(b/a) 计算角度值要加180。

• 点 (b,a) 落入第三象限(b<0, a<0) ，b/a>0，故 atan(b/a) 取值范围是 0 ~ pi/2，而此时atan2(b,a)的范围是 -pi～-pi/2

  

Parmi eux

🎜🎜Selon la définition des coordonnées sphériques, θ ∈[−π,π], ϕ∈[−π/2,π/2], r∈[0, +∞). 🎜🎜Pour θ, la période de la fonction tangente est π, donc la fonction arctangente arctan ne prend généralement qu'une seule période, son domaine est R et sa plage de valeurs est (&moins;π/ 2, π/2). Pour résoudre ce problème, la fonction Arctan, également connue sous le nom de fonction arctan2, a été introduite. 🎜🎜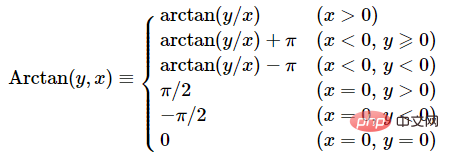🎜🎜Utilisation de la fonction atan2 atan2(delta_y, delta_x)🎜rrreee🎜Utilisation de la fonction atan atan(delta_y / delta_x)🎜rrreee🎜Similarités et différences entre atan et atan2🎜

• 🎜Le nombre de paramètres est différent🎜🎜
• 🎜Les valeurs de retour des deux sont les mêmes Radians🎜🎜
• 🎜Si delta_x est égal à 0, atan2 peut toujours être calculé, mais atan doit être jugé à l'avance, sinon cela provoquera des erreurs de programme🎜🎜
• 🎜Traitement des quadrants🎜🎜 🎜🎜🎜🎜atan2(b,a) est l'arc tangent à 4 quadrants. la valeur ne dépend pas seulement de la valeur tangente b/a , elle dépend également du quadrant dans lequel se situe le point (b, a) : 🎜
  • 🎜Lorsque le point (b, a) tombe dans le premier quadrant (b>0, a> ;0), la plage de atan2(b,a) est 0 ~ pi/2🎜🎜
  • 🎜Quand le point (b, a) tombe dans le deuxième quadrant (b>0, a< ;0), la plage de atan2(b,a) est pi/2 ~ pi🎜🎜
  • 🎜Quand le point (b, a) tombe dans le troisième quadrant (b<0, a< ;0), la plage de atan2(b,a) est -pi～-pi/2🎜🎜
  • 🎜Quand le point ( b,a) tombe dans le quatrième quadrant (b<0 , a>0), la plage de atan2(b,a) est -pi/2～0🎜🎜🎜🎜 et atan(b /a) est calculé uniquement en fonction de la valeur tangente de a/b. L'angle correspondant (peut être considéré comme simplement l'arc tangent des 2 quadrants) : 🎜
    • 🎜 Lorsque b/a > 0, la plage de valeurs de atan(b/a) C'est 0 ~ pi/2🎜🎜
    • 🎜Quand b/a < atan(b/a) est -pi/2～0</code >🎜🎜🎜🎜Plage de valeurs🎜🎜<img src="https://img.php.cn/upload/article/000/887 /227/168189146627107.png"/ alt="Comment implémenter l'angle de conversion arctan en Python" >🎜🎜<img src="https: //img.php.cn/upload/article/000/887/227/168189146672211.png"/ alt="Comment implémenter l'angle de conversion arctan en Python" >🎜<ul class=" list- paddingleft-2"><li>🎜Le point (b,a) tombe dans< When code>Le premier quadrant (b>0, a>0) ou <code>Le quatrième quadrant (b<0, a&gt ;0), atan2(b,a) = atan(b/a) 🎜🎜
    • 🎜Le point (b,a) tombe dans le Deuxième quadrant (b> 0, a<0), b/a<0, Par conséquent, la plage de valeurs de atan(b/a) est toujours -pi/2~0. atan2(b,a) est pi/2 ~ pi Par conséquent, 180 doit être ajouté à la valeur de l'angle calculée par atan(b/a). 🎜🎜
    • 🎜Le point (b,a) tombe dans le troisième quadrant (b<0, a<0), b/a>0, donc la plage de valeurs de atan(b/a ) est 0 ~ pi/2, et à ce moment la plage de atan2(b,a) est -pi~-pi/2, donc atan(b/a ) calcule l'angle La valeur est réduite de 180. 🎜🎜🎜🎜Conclusion : fonctions atan et atan2, il est recommandé d'utiliser la fonction atan2🎜

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!