Comment implémenter une permutation complète dans l'algorithme Java
Algorithme 1
implémenté basé sur la récursivité et le retour en arrière. Lorsque vous disposez 1, 2 et 3, revenez d'abord de 3 à 2 et constatez qu'il n'y a pas d'autres situations possibles, puis revenez à 1, arrangez 1, 3, 2, puis remontez jusqu'à quand il y a d'autres situations. , c'est-à-dire le nœud racine, puis lorsque vous disposez 2 comme première position, répétez le processus ci-dessus pour mettre tous les résultats possibles dans res.
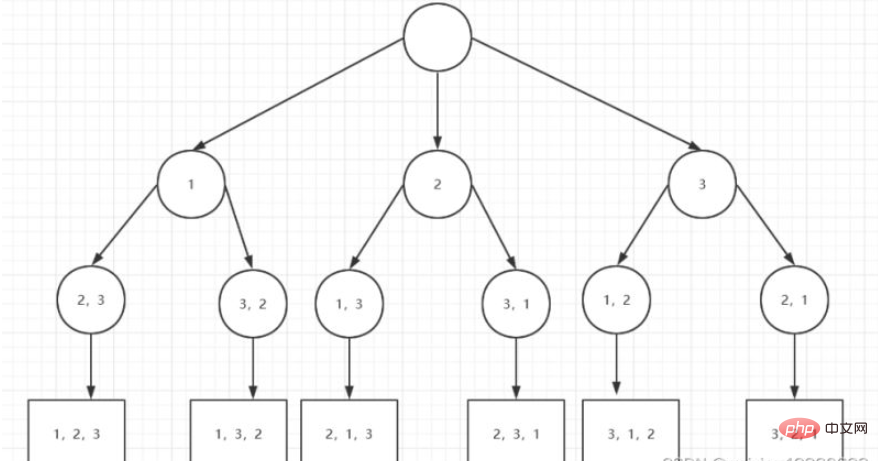
Code :
import java.util.ArrayList;
import java.util.List;
public class h718_1 {
static List<List<Integer>> res = new ArrayList<>();
public static void main(String[] args) {
int[] arr = {1,2,3};
h718_1 h2 = new h718_1();
h2.dfs(arr,new ArrayList<>());
for (List<Integer> re : res) {
System.out.println(re);
}
}
public List<List<Integer>> dfs( int[] arr,List<Integer> list){
List<Integer> temp = new ArrayList<>(list);
if (arr.length == list.size()){
res.add(temp);
}
for (int i=0;i<arr.length;i++){
if (temp.contains(arr[i])){
continue;
}
temp.add(arr[i]);
dfs(arr,temp);
temp.remove(temp.size()-1);
}
return res;
}
}Algorithme 2
Réalisez une permutation complète en échangeant des positions : Supposons que l'ensemble soit {1, 2, 3, 4}
Cycle d'échange de positions : 1 et 1 sont échangés ; sont échangés ; 1 et 3 sont échangés ; 1 et 4 sont échangés
Chaque échange appelle un ensemble plus petit de manière récursive :
Par exemple : le premier échange de 1 et 1 détermine que 1 est en premier lieu, il peut donc être considéré comme {1} + échange récursif {2,3,4} ;
Le premier échange de 1 et 2 détermine que 2 est en premier lieu, il peut donc être considéré comme {2} + échange récursif {1,3 ,4};
La première fois 1 L'échange avec 3 détermine que 3 est en premier lieu, il peut donc être considéré comme {3} + échange récursif {1,2,4};
Le premier échange de 1 et 4 détermine que 4 est en premier lieu, il peut donc être considéré comme {4 } + échange récursif {1,2,3} ;
et ainsi de suite.
Code :
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class h718_2 {
static List<List<Integer>> res = new ArrayList<>();
public static void main(String[] args) {
int[] arr = {1,2,3};
h718_2 h3 = new h718_2();
h3.pailie_swap(0,arr);
}
public void pailie_swap(int index, int[] arr){
if (arr.length==index){
System.out.println(Arrays.toString(arr));
return;
}
for (int i = index;i<arr.length;i++){
swap(i,index,arr);
pailie_swap(index+1,arr);
swap(i,index,arr);
}
}
public void swap(int i,int j ,int[] arr){
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
}Algorithme 3
Vous pouvez obtenir un arrangement complet en ajoutant des éléments :
Définissez d'abord une liste et placez-y le premier élément, puis insérez les éléments restants dans l'ordre dans toutes les positions possibles des éléments de l'ensemble précédent ; Générez une nouvelle liste ;
Par exemple : pour obtenir un arrangement complet de {1,2,3,4}
Définissez d'abord une liste et ajoutez le premier élément comme {1}, puis le deuxième élément 2 peut être inséré dans { ; 1} Les deux positions avant et après forment une nouvelle liste : {21, 12}, et le troisième élément 3 est inséré dans toutes les positions des éléments de la liste : {321, 231, 213, 312, 132, 123} ; et ainsi de suite.
Code :
import java.util.ArrayList;
public class h718_3 {
public static void main(String[] args) {
String aa = "123";
h718_3 h4 = new h718_3();
ArrayList<String> res = new ArrayList<>();
res = h4.getPermutation0(aa);
for (String re : res) {
System.out.println(re);
}
}
public ArrayList<String> getPermutation0(String A) {
int n = A.length();
ArrayList<String> res = new ArrayList<>();
res.add(A.charAt(0) + "");//初始化,包含第一个字符
for (int i = 1; i < n; i++) {//第二个字符插入到前面生成集合的每个元素里面
ArrayList<String> res_new = new ArrayList<>();
char c = A.charAt(i);//新字符
for (String str : res) {//访问上一趟集合中的每个字符串
// 插入到每个位置,形成一个新串
String newStr = c + str;//加在前面
res_new.add(newStr);
newStr = str + c;//加在后面
res_new.add(newStr);
//加在中间
for (int j = 1; j < str.length(); j++) {
newStr = str.substring(0, j) + c + str.substring(j);
res_new.add(newStr);
}
}
res = res_new;//更新
}
return res;
}
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Guide de la racine carrée en Java. Nous discutons ici du fonctionnement de Square Root en Java avec un exemple et son implémentation de code respectivement.
 Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre parfait en Java. Nous discutons ici de la définition, comment vérifier le nombre parfait en Java ?, des exemples d'implémentation de code.
 Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Guide du générateur de nombres aléatoires en Java. Nous discutons ici des fonctions en Java avec des exemples et de deux générateurs différents avec d'autres exemples.
 Weka en Java
Aug 30, 2024 pm 04:28 PM
Weka en Java
Aug 30, 2024 pm 04:28 PM
Guide de Weka en Java. Nous discutons ici de l'introduction, de la façon d'utiliser Weka Java, du type de plate-forme et des avantages avec des exemples.
 Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre de Smith en Java. Nous discutons ici de la définition, comment vérifier le numéro Smith en Java ? exemple avec implémentation de code.
 Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Dans cet article, nous avons conservé les questions d'entretien Java Spring les plus posées avec leurs réponses détaillées. Pour que vous puissiez réussir l'interview.
 Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Java 8 présente l'API Stream, fournissant un moyen puissant et expressif de traiter les collections de données. Cependant, une question courante lors de l'utilisation du flux est: comment se casser ou revenir d'une opération FOREAK? Les boucles traditionnelles permettent une interruption ou un retour précoce, mais la méthode Foreach de Stream ne prend pas directement en charge cette méthode. Cet article expliquera les raisons et explorera des méthodes alternatives pour la mise en œuvre de terminaison prématurée dans les systèmes de traitement de flux. Lire plus approfondie: Améliorations de l'API Java Stream Comprendre le flux Forach La méthode foreach est une opération terminale qui effectue une opération sur chaque élément du flux. Son intention de conception est
 Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Guide de TimeStamp to Date en Java. Ici, nous discutons également de l'introduction et de la façon de convertir l'horodatage en date en Java avec des exemples.






