

La récursion est en effet une logique mathématique relativement abstraite, qui peut être simplement comprise comme "le programme appelle son propre algorithme".
L'explication de la récursion par Wikipédia est la suivante :
La récursion (anglais : récursion), également traduite par récursivité, en mathématiques et en informatique, fait référence à la méthode d'utilisation de la fonction elle-même dans la définition de la fonction. Le terme récursivité est également plus couramment utilisé pour décrire le processus de répétition de choses de manière auto-similaire.
Par exemple, lorsque deux miroirs sont approximativement parallèles entre eux, les images imbriquées dans les miroirs apparaissent sous forme de récursion infinie. Cela peut également être compris comme le processus d’auto-réplication.
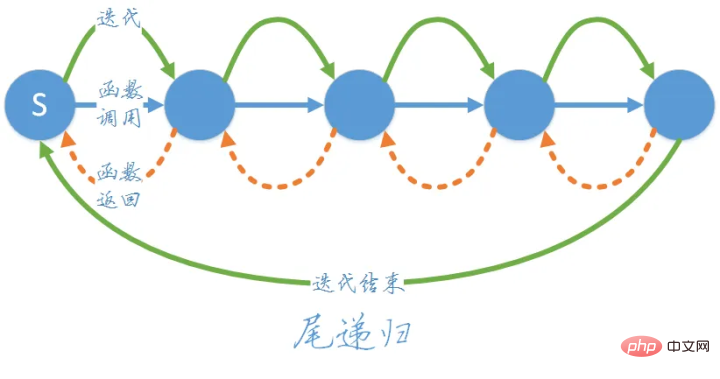
« Passer » signifie transmettre et « Retour » signifie revenir. Passez d'abord une méthode couche par couche, puis transmettez-la à la dernière couche et renvoyez le résultat.
Par exemple, je faisais la queue pour un test d'acide nucléique, et il y avait 100 personnes devant moi. Je voulais demander quand le personnel médical quitterait le travail, alors j'ai demandé au frère en face de moi. , et il a demandé aux personnes devant lui, en le transmettant un à un. Finalement, il a été transmis au personnel médical, qui a répondu qu'ils quitteraient le travail à 18 heures. Cette phrase m'a été renvoyée et m'est finalement parvenue. J'ai appris que le personnel médical avait quitté le travail à six heures.
Ce processus est un processus récursif. Si « transmettre un message » lui-même est une méthode, alors l'ensemble du processus de transmission d'un message appelle sa propre méthode et obtient finalement le résultat.
C'est différent du cycle. Le cycle équivaut à mettre des écouteurs sur tout le monde, et ensuite un "intermédiaire" vous demandera un par un si vous savez quand le personnel médical quittera le travail. Lorsque vous demanderez au personnel médical, vous aurez la réponse. L'« agent » m'a dit que je quitterais le travail à six heures.
Essentiellement, la récursivité consiste à démonter continuellement un gros problème, comme éplucher un oignon, et enfin à le démonter au plus petit niveau, et à renvoyer le résultat de la solution.
Utilisez Python pour donner l'exemple le plus simple d'une fonction récursive et parler de ce que sont les applications récursives.
Nous voyons souvent des fonctions s'appeler pour implémenter des opérations de boucle, telles que des fonctions permettant de trouver des factorielles.
La factorielle de l'entier n est n*(n-1)*(n-2)*...*3*2*1.
Par exemple, les 5 lignes suivantes de code Python peuvent réaliser le calcul factoriel.
def fact(n): ''' n表示要求的数的阶乘 ''' if n==1: return n n = n*fact(n-1) return n print(factorial(5))
Beaucoup de gens peuvent être confus au sujet de la logique de calcul ici, pourquoi la fonction de fait s'appelle et obtient finalement le résultat.
On peut le déduire selon la logique mathématique :
La factorielle de l'entier n est : fact(n) = n*(n-1)*...*3*2*1.
La factorielle de l'entier n-1 est : fact(n-1) = (n-1)*(n-2)*...*3*2*1.
On peut donc en déduire que fact(n) = n*fact(n-1).
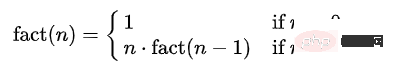
Existe-t-il une méthode de faits qui peut être appelée pour chaque nombre ? Lorsque n=1 est finalement appelé, la factorielle du résultat n est renvoyée.
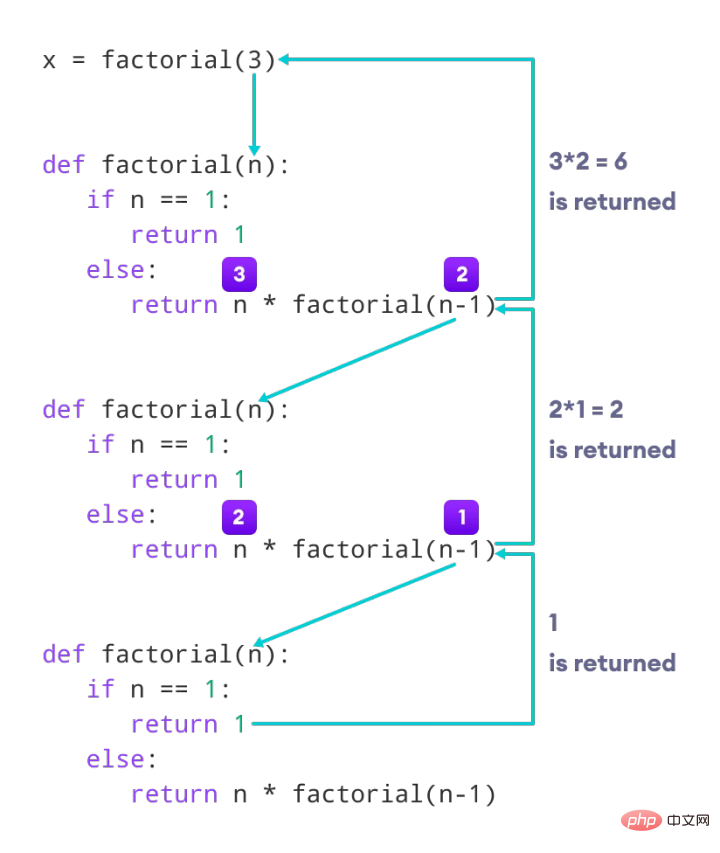
Regardez l'image ci-dessus, la fonction récursive sera appelée couche par couche, et enfin lorsque n=1, le résultat sera renvoyé vers le haut.
C'est tout le processus de récursion. Si nous donnons une définition précise de la récursion, elle peut être résumée par les trois points suivants :
1. Il existe au moins une condition finale claire pour la récursion.
2. Donnez la solution lorsque la récursion se termine.
3. Chaque fois que vous entrez dans un niveau de récursion plus profond, la taille du problème (montant du calcul) doit être réduite par rapport à la dernière récursion.
Prenons le code ci-dessus comme exemple :
def factorial(n): ''' n表示要求的数的阶乘 ''' if n==1: # 1、明确递归终止条件; return n # 2、递归终止时的处理办法 n = n*factorial(n-1) # 递去 return n# 归来
En plus des cas factoriels courants, il existe également des séquences de Fibonacci, qui sont également des utilisations classiques de la récursivité.
Séquence de Fibonacci : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Cette séquence commence à partir du 3ème élément, chaque élément est égal à la somme des deux éléments précédents.
Il est défini récursivement comme suit : F(0)=0, F(1)=1, F(n)=F(n - 1)+F(n - 2)(n≥ 2, n∈N* ).
En Python, nous pouvons utiliser des fonctions récursives pour implémenter la séquence de Fibonacci :
# 1,1,2,3,5,8,13,21,34,55,试判断数列第12个数是哪个? def fab(n): ''' n为斐波那契数列 ''' if n <= 2: v = 1 return v v = fab(n-1)+fab(n-2) return v print(fab(12))
Utiliser des méthodes mathématiques pour dériver :
En fait, les deux cas récursifs ci-dessus peuvent s'expliquer par l'induction mathématique, qui est la connaissance des mathématiques au lycée.
Généralement, pour prouver une proposition P(n) liée à un nombre naturel n, il y a les étapes suivantes :
(1) Prouver que la proposition est vraie lorsque n prend la première valeur n0. n0 prend la valeur 0 ou 1 pour les séquences générales, mais il existe aussi des cas particuliers.
(2) Supposons que la proposition est vraie lorsque n=k (k≥n0, k est un nombre naturel), et prouvez que la proposition est également vraie lorsque n=k+1.
En synthétisant (1) (2), pour tous les nombres naturels n (≥n0), la proposition P(n) est vraie.
En plus des explications mathématiques, j'ai également vu quelqu'un donner une explication plus vivante de la récursivité auparavant :
1、我们已经完成了吗?如果完成了,返回结果。如果没有这样的终止条件,递归将会永远地继续下去。
2、如果没有,则简化问题,解决较容易的问题,并将结果组装成原始问题的解决办法。然后返回该解决办法。
哈哈,到这里大家是不是对递归有了一个更加深刻的认识。
如果还不清楚,没关系,这里还有更多的递归案例,用Python来实现,可以说非常简洁。
def gcd(m, n): if n == 0: return m else: return gcd(n, m%n)
def sumnums(n): if n == 1: return 1 return n + sumnums(n - 1) print(sumnums(3))
def reverse(string): if len(string) == 0: return string else: return reverse(string[1:]) + string[0] reverseme = '我是帅哥' print(reverse(reverseme))
def towerOfHanoi(numrings, from_pole, to_pole, aux_pole):
if numrings == 1:
print('Move ring 1 from', from_pole, 'pole to', to_pole, 'pole')
return
towerOfHanoi(numrings - 1, from_pole, aux_pole, to_pole)
print('Move ring', numrings, 'from', from_pole, 'pole to', to_pole, 'pole')
towerOfHanoi(numrings - 1, aux_pole, to_pole, from_pole)
numrings = 2
towerOfHanoi(numrings, 'Left', 'Right', 'Middle')
data = [1,3,6,13,56,123,345,1024,3223,6688]
def dichotomy(min,max,d,n):
'''
min表示有序列表头部索引
max表示有序列表尾部索引
d表示有序列表
n表示需要寻找的元素
'''
mid = (min+max)//2
if mid==0:
return 'None'
elif d[mid]<n:
print('向右侧找!')
return dichotomy(mid,max,d,n)
elif d[mid]>n:
print('向左侧找!')
return dichotomy(min,mid,d,n)
else:
print('找到了%s'%d[mid])
return
res = dichotomy(0,len(data),data,222)
print(res)
有位大佬说过:To Iterate is Human, to Recurse, Divine。
中文译为:人理解迭代,神理解递归。
可见递归是非常神奇的算法,它的神奇之处在于它允许用户用有限的语句描述无限的对象。
当然人无完人,递归也是有缺点的,它一般效率较低,且会导致调用栈溢出。
因为递归不断调用自身函数,且产生大量变量,而栈空间的容量是有限的,循环太多就会效率低下,甚至导致调用栈溢出。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!