Comment utiliser le tas pour résoudre le problème Top-k en Java ?

1. Qu'est-ce qu'un tas ?

Structure du tas

Le tas est en fait une sorte d'arbre binaire, mais les arbres binaires ordinaires stockent les données dans une structure en chaîne, tandis que les tas stockent les données séquentiellement dans des tableaux. Alors, quel type d’arbre binaire convient au stockage séquentiel ?

Nous supposons qu'un arbre binaire ordinaire peut être stocké dans un tableau, nous pouvons alors obtenir la structure suivante :

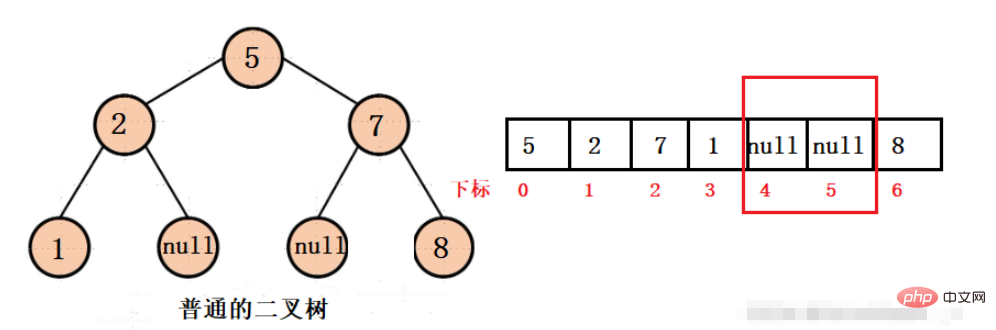
Nous pouvons voir que lorsqu'il y a une valeur nulle au milieu de l'arbre binaire, l'espace de stockage de la baie sera gaspillé, alors que se passe-t-il pour que l'espace ne soit pas gaspillé ? C'est un arbre binaire complet.

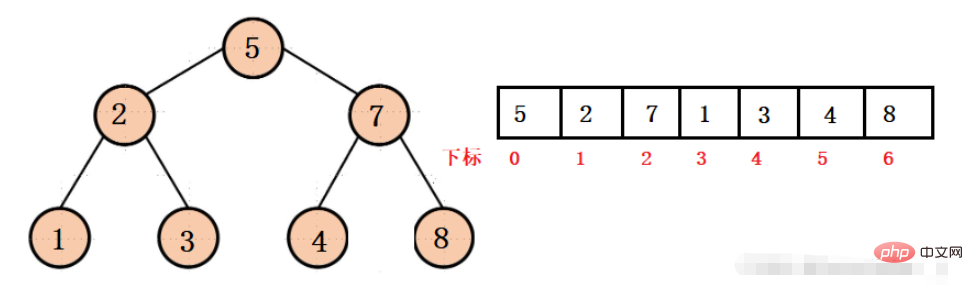
À partir de la structure ci-dessus, nous ne pouvons pas utiliser le pointeur de la structure de chaîne pour accéder au nœud enfant ou au nœud parent. Nous ne pouvons y accéder que via l'indice correspondant, ce qui est en fait relativement simple.

Par exemple, dans l'image ci-dessous :

On sait que l'indice de 2 nœuds est 1, alors

L'indice de son enfant de gauche est : 2 * 2 + 1 = 3

L'indice de son enfant de droite est : 2 * 2 + 2 = 4

Au contraire, on sait que l'indice du nœud 1 est 3 et l'indice du nœud 3 est 4, puis l'indice du nœud parent du nœud

1 est : (3 - 1) / 2 = 1

3 nœuds L'indice du nœud parent est : (4 - 1) / 2 = 1

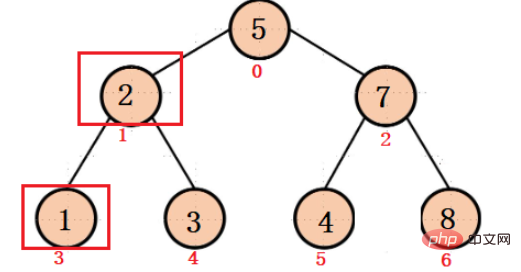
Grand tas de racines VS petit tas de racines

Grand tas de racines (tas maximum )

Le grand tas racine garantit que le nœud racine de chaque arbre binaire est plus grand que la gauche et la droite. Le nœud enfant

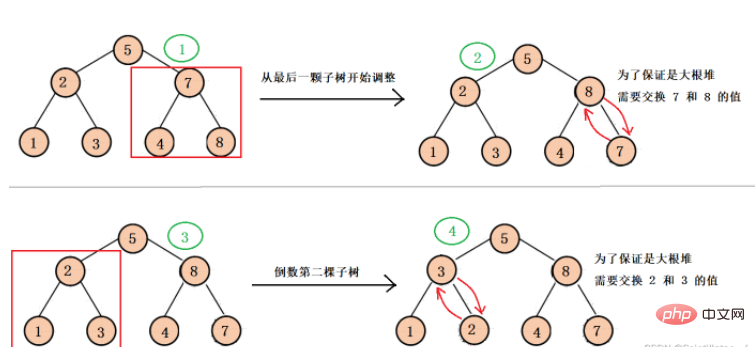
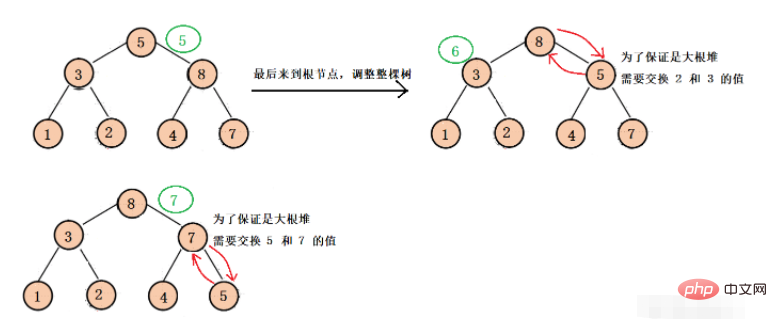
commence à s'ajuster du nœud racine du dernier sous-arbre au nœud racine de chaque sous-arbre, de sorte que chaque Le sous-arbre est ajusté vers le bas jusqu'à un grand tas de racines, et effectue finalement l'ajustement final vers le bas pour garantir que l'arbre binaire entier est un grand tas (cet ajustement est principalement destiné au tri ultérieur du tas).

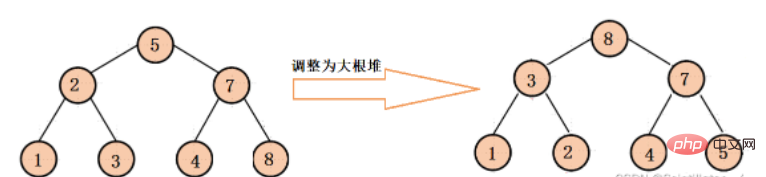
Le processus d'ajustement spécifique est le suivant :

Comment l'implémenter avec du code ?

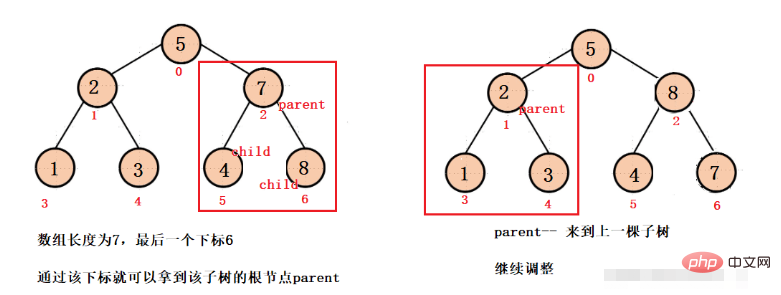
Nous ajustons d'abord à partir du dernier sous-arbre, puis nous devons obtenir le nœud racine parent du dernier sous-arbre. Nous savons que le dernier indice de nœud du tableau est len ​​- 1, et ce nœud est l'enfant gauche du dernier sous-arbre. .Ou le bon enfant, selon l'indice enfant, vous pouvez obtenir l'indice du nœud racine (parent), parent - vous pouvez ajuster chaque sous-arbre jusqu'à ce que vous atteigniez le nœud racine, puis ajuster vers le bas pour la dernière fois, vous pouvez obtenir. Gros tas de racines.

// 将数组变成大根堆结构
public void createHeap(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        elem[i] = arr[i];// 放入elem[],假设不需要扩容
        usedSize++;
    }
    // 得到根节点parent, parent--依次来到每颗子树的根节点，
    for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
        // 依次向下搜索，使得每颗子树都变成大根堆
        shiftDown(parent,usedSize);
    }
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
    int child = parent*2+1;// 拿到左孩子
    while (child < len){
        // 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较 
        if (child+1 < len && (elem[child] < elem[child+1])){
            child++;
        }
        // 比较较大的孩子和父节点,看是否要交换
        int max = elem[parent] >= elem[child] ? parent : child;
        if (max == parent) break;// 如果不需要调整了，说明当前子树已经是大根堆了，直接 break
        swap(elem,parent,child);
        parent = child;// 继续向下检测，看是否要调整
        child = parent*2+1;
    }
}
public void swap(int[] arr,int i,int j){
  	int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

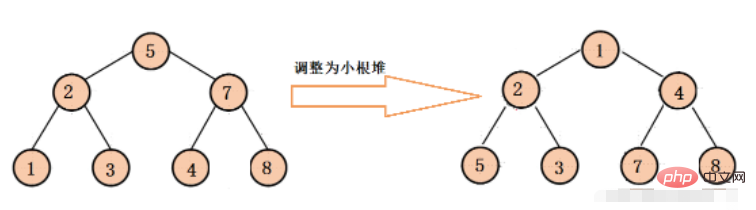
Petit tas racine (tas minimum)

Le petit tas racine garantit que le nœud racine de chaque arbre binaire est plus petit que les nœuds enfants gauche et droit

Le processus d'ajustement est le même que ci-dessus.

File d'attente prioritaire (PriorityQueue)

En Java, une structure de données de tas (PriorityQueue) est fournie, également appelée file d'attente prioritaire. Lorsque nous créons un tel objet, nous obtenons un objet sans données ajoutées. Nous pouvons ajouter ou. supprimer des éléments dans le petit tas racine. Chaque fois que nous supprimons ou y ajoutons un élément, le système effectuera un ajustement global et le réajustera sur un petit tas racine.

// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2，剩余最小的元素就是11，会被调整到堆顶，下一次弹出
System.out.println(smallHeap.poll());// 弹出11

 // 如果需要得到大根堆，在里面传一个比较器
 PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
     @Override
     public int compare(Integer o1, Integer o2) {
         return o2 - o1;
     }
 });

2. Idées pour résoudre les problèmes top-k

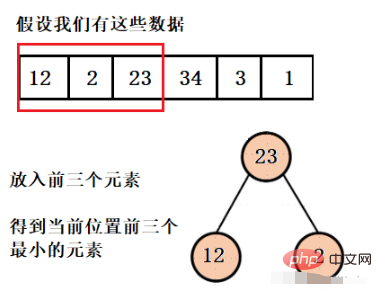
Exemple : Il y a un tas d'éléments et il vous est demandé de trouver les trois premiers plus petits éléments.

Idée 1 : Triez le tableau de petit à grand et obtenez les 3 premiers éléments du tableau. Cependant, on peut constater que la complexité temporelle de cette méthode est trop élevée et n’est pas recommandée.

Idée 2 : placez tous les éléments dans une structure de tas, puis faites apparaître trois éléments. Chaque élément contextuel est le plus petit du tas actuel, puis les trois éléments qui apparaissent sont les trois plus petits éléments du passé.

Cette idée peut être réalisée, mais en supposant que j'ai 1 000 000 d'éléments et que je n'affiche que les trois premiers éléments les plus petits, alors un tas de taille 1 000 000 sera utilisé. La complexité spatiale de cette opération est trop élevée, cette méthode n'est donc pas recommandée.

Trois idées :

Nous devons obtenir les trois plus petits éléments, puis construire un tas d'une taille de 3. Supposons que la structure de tas actuelle est exactement remplie de 3 éléments, alors ces trois éléments sont les trois plus petits éléments actuels. éléments. En supposant que le quatrième élément est l'un des éléments que nous voulons, alors au moins un des trois premiers éléments n'est pas ce que nous voulons et il doit être affiché. Alors, qui doit apparaître ?

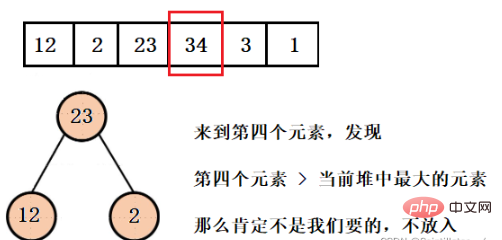
Ce que nous voulons obtenir, ce sont les trois premiers plus petits éléments, donc le plus grand élément de la structure de tas actuelle ne doit pas être ce que nous voulons, donc ici nous construisons un grand tas racine. Pop l'élément, puis insérez le quatrième élément jusqu'à ce que tout le tableau soit parcouru.

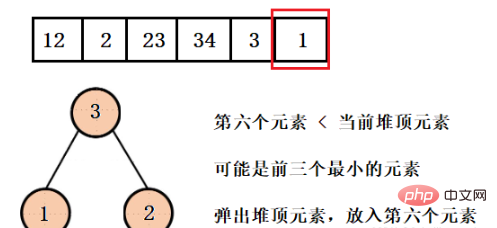
这样我们就得到了只含有前三个最小元素的堆，并且可以看到堆的大小一直都是3，而不是有多少数据就建多大的堆，然后再依次弹出元素就行了。

// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
     // 创建一个大小为 k的大根堆
     PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
         @Override
         public int compare(Integer o1, Integer o2) {
             return o2 - o1;
         }
     });
     for (int i = 0; i < arr.length; i++) {
         if (i < k){
             // 放入前 k 个元素
             maxHeap.offer(arr[i]);
         }else{
             // 从第 k+1个元素开始进行判断是否要入堆
             if (maxHeap.peek() > arr[i]){
                 maxHeap.poll();
                 maxHeap.offer(arr[i]);
             }
         }
     }
     int[] ret = new int[k];
     for (int i = 0; i < k; i++) {
         ret[i] = maxHeap.poll();
     }
     return ret;
 }

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!