Quelles sont les connaissances et concepts de base des arbres binaires en Java ?

1. Structure arborescente

1.1 Concept

L'arbre est une structure de données non linéaire, qui est un ensemble de relations hiérarchiques composées de n (n>=0) nœuds limités. On l’appelle arbre parce qu’il ressemble à un arbre à l’envers, c’est-à-dire qu’il a les racines tournées vers le haut et les feuilles tournées vers le bas.

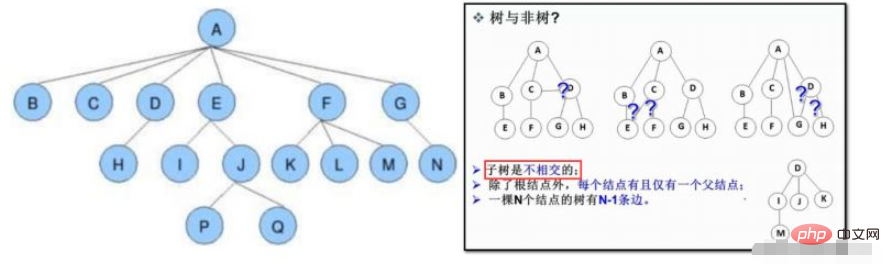
1.2 Concept (Important)

a Le degré du nœud : le nombre de sous-arbres du nœud comme indiqué ci-dessus : le degré de A est 6, le degré de J est 2

b. degré de l'arbre : le numéro de l'arbre , le degré du plus grand nœud est le degré du nombre comme indiqué dans la figure ci-dessus : le degré de l'arbre est 6

c Nœud feuille (nœud terminal) : a. nœud de degré 0 (nœud sans sous-arbre)

d. Nœud parent Point/nœud parent : Comme indiqué dans l'image ci-dessus : D est le nœud parent de H

Nœud enfant/nœud enfant : Comme indiqué dans l'image ci-dessus : H est le nœud enfant de D

e. Nœud racine : Un nœud sans parents comme indiqué dans l'image ci-dessus : A

f .Le niveau du nœud : à partir de la définition de la racine, la racine est le premier niveau, les nœuds enfants de la racine sont le deuxième niveau, et ainsi de suite ;

g La hauteur ou la profondeur de l'arbre : le niveau maximum du nœud dans l'arbre comme indiqué ci-dessus : La hauteur de l'arbre est. 4

2. Arbre binaire (point clé)

2.1 Concept

Chaque nœud a au plus deux sous-arbres, degré

2.2 La forme de base de l'arbre binaire

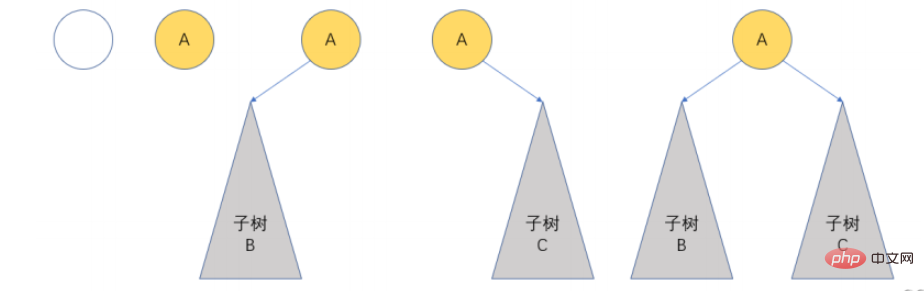
2.3 Deux types d'arbre binaire spécial

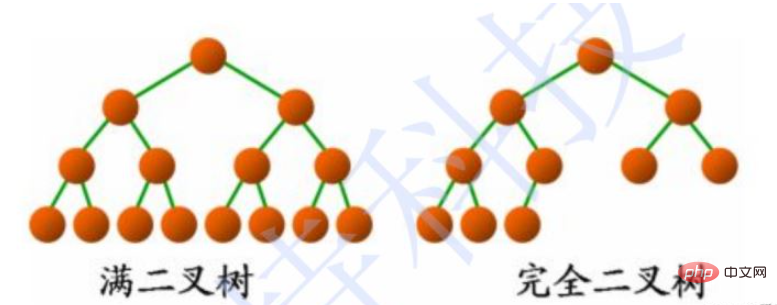
a. Arbre binaire complet : le degré non cotylédon est 2

b Arbre binaire complet : il manque le "coin inférieur droit" de l'arbre binaire

2.4 Propriétés des arbres binaires

a. arbre

1. La hauteur est K, alors il y a 2^k-1 nœuds

2 Le niveau est K, alors la couche a 2^(k-1) nœuds

3. de nœuds - 1

4. Il y a n0 de degré 0 et n2 de degré 2, alors n0 = n2 + 1

b Arbre binaire complet

1. enfant gauche

2. Il ne peut y avoir qu'un seul nœud de degré 1

2.5 Stockage de l'arbre binaire

La structure de stockage de l'arbre binaire est divisée en : stockage séquentiel et stockage lié similaire à la liste chaînée.

Stockage séquentiel : seuls les arbres binaires complets peuvent être stockés

Stockage en chaîne : arbres binaires ordinaires

Cette fois, nous montrons le stockage en chaîne

Le stockage en chaîne des arbres binaires est référencé par les nœuds un par un La représentation commune est binaire et. représentation ternaire,

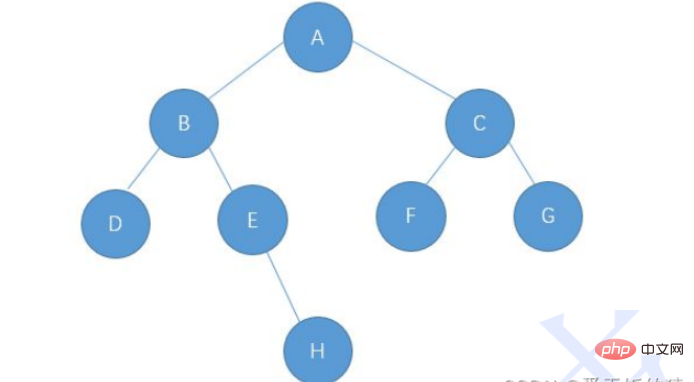
prenez cette photo comme exemple, les détails sont les suivants :

// 孩子表示法
private static class TreeNode{
    char val;
    TreeNode left;
    TreeNode right;
 
    public TreeNode(char val) {
        this.val = val;
    }
}

Initialisation :

    public static TreeNode build(){
        TreeNode nodeA=new TreeNode('A');
        TreeNode nodeB=new TreeNode('B');
        TreeNode nodeC=new TreeNode('C');
        TreeNode nodeD=new TreeNode('D');
        TreeNode nodeE=new TreeNode('E');
        TreeNode nodeF=new TreeNode('F');
        TreeNode nodeG=new TreeNode('G');
        TreeNode nodeH=new TreeNode('H');
        nodeA.left=nodeB;
        nodeA.right=nodeC;
        nodeB.left=nodeD;
        nodeB.right=nodeE;
        nodeE.right=nodeH;
        nodeC.left=nodeF;
        nodeC.right=nodeG;
        return nodeA;
    }

2.6 Opérations de base des arbres binaires

2.6.1 Traversée d'arbre binaire (récursion)

1. NLR : ancien parcours de précommande (également connu sous le nom de parcours de précommande) - visitez le nœud racine ---> le sous-arbre gauche de la racine --->

    //先序遍历 : 根左右
    public static void preOrder(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

2. LNR : Inorder Traversal (Inorder Traversal)—— Le sous-arbre gauche de la racine --->

    //中序遍历
    public static void inOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        System.out.print(root.val+" ");
        preOrder(root.right);
    }

3. LRN : Postorder Traversal - sous-arbre gauche de la racine ---> sous-arbre droit du nœud racine --->

    //后序遍历
    public static void postOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.val+" ");
    }

2.6.2 Traversée d'arbre binaire (itération)

1. Traversée de pré-ordre

    //方法2(迭代)
    //先序遍历 (迭代)
    public static void preOrderNonRecursion(TreeNode root){
        if(root==null){
            return ;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode cur=stack.pop();
            System.out.print(cur.val+" ");
            if(cur.right!=null){
                stack.push(cur.right);
            }
            if(cur.left!=null){
                stack.push(cur.left);
            }
        }
    }

2. Traversée d'ordre inverse

    //方法2(迭代)
    //中序遍历 (迭代)
    public static void inorderTraversalNonRecursion(TreeNode root) {
        if(root==null){
            return ;
        }
 
        Deque<TreeNode> stack=new LinkedList<>();
        // 当前走到的节点
        TreeNode cur=root;
        while (!stack.isEmpty() || cur!=null){
            // 不管三七二十一，先一路向左走到根儿~
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            // 此时cur为空，说明走到了null，此时栈顶就存放了左树为空的节点
            cur=stack.pop();
            System.out.print(cur.val+" ");
            // 继续访问右子树
            cur=cur.right;
        }
    }

3. nœuds (récursion et itération)

    //方法2(迭代)
    //后序遍历 (迭代)
    public static void postOrderNonRecursion(TreeNode root){
        if(root==null){
            return;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        TreeNode cur=root;
        TreeNode prev=null;
 
        while (!stack.isEmpty() || cur!=null){
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
 
            cur=stack.pop();
            if(cur.right==null || prev==cur.right){
                System.out.print(cur.val+" ");
                prev=cur;
                cur=null;
            }else {
                stack.push(cur);
                cur=cur.right;
            }
        }
    }

2. Trouvez le nombre de nœuds feuilles (récursion et itération)

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树中一共有多少个节点，返回节点数
    //此时的访问就不再是输出节点值，而是计数器 + 1操作
    public static int getNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        return 1+getNodes(root.left)+getNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计当前树中的节点个数
    public static int getNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            size++;
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        return size;
    }

3 Trouvez le nombre de nœuds dans la kème couche

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树的叶子结点个数
    public static int getLeafNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        if(root.left==null && root.right==null){
            return 1;
        }
        return getLeafNodes(root.left)+getLeafNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计叶子结点的个数
    public static int getLeafNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            TreeNode cur=queue.poll();
            if(cur.left==null && cur.right==null){
                size++;
            }
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
        }
        return size;
    }

4. Trouvez la hauteur de l'arbre

    //求出以root为根节点的二叉树第k层的节点个数
    public static int getKLevelNodes(TreeNode root,int k){
        if(root==null || k<=0){
            return 0;
        }
        if(k==1){
            return 1;
        }
        return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
    }

. 5. Déterminez s'il existe un nœud avec une valeur dans le numéro de l'arbre binaire

    //传入一个以root为根节点的二叉树，就能求出该树的高度
    public static int height(TreeNode root){
        if(root==null){
            return 0;
        }
        return 1+ Math.max(height(root.left),height(root.right));
    }

2.7 Parcours par ordre de niveau de l'arbre binaire

    //判断当前以root为根节点的二叉树中是否包含指定元素val，
    //若存在返回true，不存在返回false
    public static boolean contains(TreeNode root,char value){
        if(root==null){
            return false;
        }
        if(root.val==value){
            return true;
        }
        return contains(root.left,value) || contains(root.right,value);
    }

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!