
Le tri par sélection est un algorithme de tri simple et intuitif Quelles que soient les données saisies, la complexité temporelle est O(n²). Ainsi, lors de son utilisation, plus la taille des données est petite, mieux c'est. Le seul avantage est peut-être qu'il n'occupe pas d'espace mémoire supplémentaire. Tout d'abord, recherchez le plus petit (grand) élément de la séquence non triée et stockez-le à la position de départ de la séquence triée.
Continuez à trouver le plus petit (grand) élément parmi les éléments non triés restants, puis placez-le à la fin de la séquence triée. 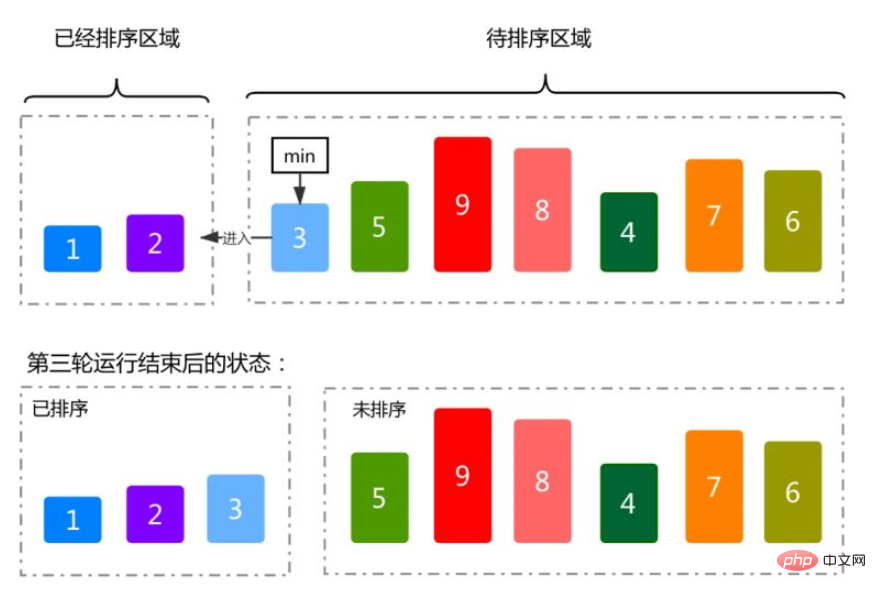
public static void selectSort(int[] arr) {
//选择排序
if(arr == null || arr.length < 2) {
return;
}
int n = arr.length;
for (int i = 0; i < n; i++) {
int minValueIndex = i;
for (int j = i+1; j < n; j++) {
minValueIndex = arr[j] < arr[minValueIndex] ? j : minValueIndex;
}
swap(arr,i,minValueIndex);
}
}
public static void swap(int[] arr,int i,int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {7,5,1,9,4,2,6};
printArray(arr);
selectSort(arr);
printArray(arr);
}2. Tri à bulles
**Le principe de l'algorithme de tri à bulles est le suivant : **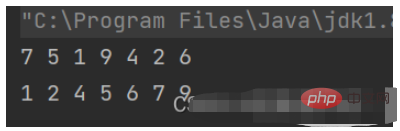
public static void bubbleSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
int n = arr.length;
for (int i = n-1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
if(arr[j] > arr[j+1]) {
swap(arr,j,j+1);
}
}
}
}
public static void swap(int[] arr,int i,int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] arr = {14,6,3,10,2};
printArray(arr);
bubbleSort(arr);
printArray(arr);
}3. Tri par insertion
Le tri par insertion signifie que parmi les éléments à trier, en supposant que les premiers n-1 (où n>=2) nombres sont déjà dans l'ordre, maintenant le nième numéro Insérez-le dans la séquence qui a été triée auparavant, puis trouvez une position qui vous convient, de sorte que la séquence dans laquelle le nième nombre est inséré soit également triée. Le processus d'insertion de tous les éléments selon cette méthode jusqu'à ce que la séquence entière soit en ordre est appelé tri par insertion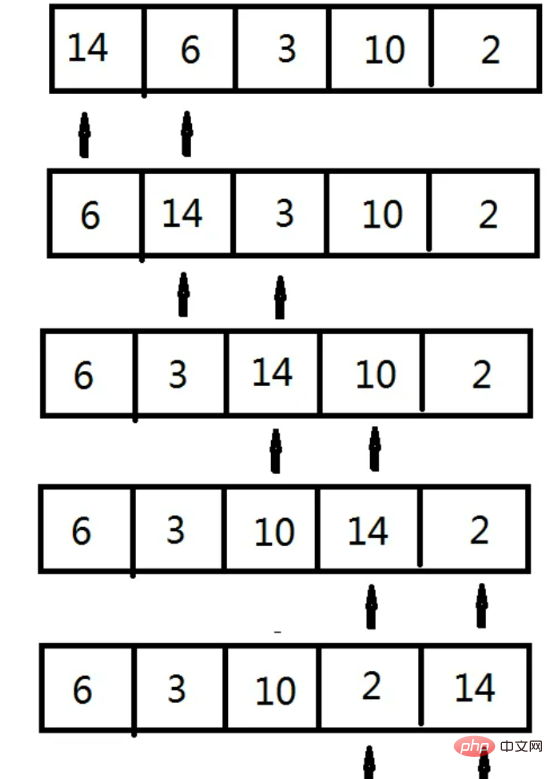
public static void insertSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
int n = arr.length;
for (int i = 1; i < n; i++) {
int currIndex = i;
while(currIndex - 1 >= 0 && arr[currIndex-1] > arr[currIndex]) {
swap(arr,currIndex,currIndex-1);
currIndex--;
}
}
}
public static void swap(int[] arr,int i,int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
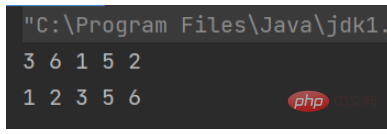
int[] arr = {3,6,1,5,2};
printArray(arr);
insertSort(arr);
printArray(arr);
} Optimisation du tri par insertion
Optimisation du tri par insertion
public static void insertSort1(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
int n = arr.length;
for (int i = 1; i < n; i++) {
for (int j = i-1; j >= 0; j--) {
if(arr[j] > arr[j+1]) {
swap(arr,j,j+1);
}else {
break;
}
}
}
}
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!