Comment implémenter un graphe non orienté en Java ?

Concepts de base

Définition d'un graphe

Un graphe est composé d'un ensemble de points V={v_i} et d'un ensemble E={e_k} de paires d'éléments non ordonnés dans VV Un binaire groupe, enregistré sous la forme G=(V,E), l'élément v_i dans V est appelé un sommet et l'élément e_k dans E est appelé une arête.

Pour deux points u, v dans V, si l'arête (u, v) appartient à E, alors les deux points u et v sont dits adjacents, et u et v sont appelés les extrémités de l'arête (u, v).

Nous pouvons utiliser m(G)=|E| pour représenter le nombre d'arêtes dans le graphe G, et n(G)=|V| pour représenter le nombre de sommets dans le graphe G.

Définition d'un graphe non orienté

Pour toute arête (vi, vj) dans E, si les extrémités de l'arête (vi, vj) ne sont pas ordonnées, il s'agit d'une arête non orientée. A ce moment, le graphe G est appelé non orienté. graphique. Le graphe non orienté est le modèle de graphe le plus simple. L'image suivante montre le même graphe non orienté. Les sommets sont représentés par des cercles, et les arêtes sont les connexions entre les sommets sans flèches (image de "Algorithm 4th Edition") :

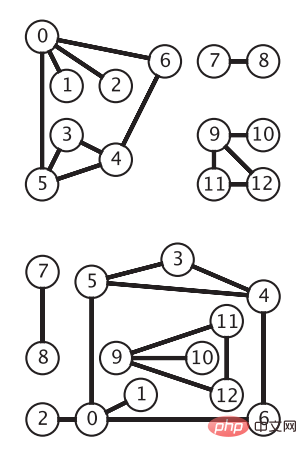
API de graphe non orienté

Pour un graphe non orienté, nous nous soucions du nombre de sommets, du nombre d'arêtes, des sommets adjacents de chaque sommet et de l'opération d'ajout d'arêtes, donc l'interface est la suivante :

package com.zhiyiyo.graph;

/**
 * 无向图
 */
public interface Graph {
    /**
     * 返回图中的顶点数
     */
    int V();

    /**
     * 返回图中的边数
     */
    int E();

    /**
     * 向图中添加一条边
     * @param v 顶点 v
     * @param w 顶点 w
     */
    void addEdge(int v, int w);

    /**
     * 返回所有相邻顶点
     * @param v 顶点 v
     * @return 所有相邻顶点
     */
    Iterable<Integer> adj(int v);
}

L'implémentation de l'API non orientée graph

Matrice de contiguïté

L'utilisation d'une matrice pour représenter un graphique est souvent plus pratique pour étudier les propriétés et les applications des graphiques. Il existe différentes représentations matricielles pour divers graphiques, telles que les matrices de poids et les matrices de contiguïté. la matrice de contiguïté. Il est défini comme :

Pour le graphe G=(V,E), |V|=n, construire une matrice A=(a_ij)_n×n, où :

est appelé une matrice A est la matrice de contiguïté du graphe G.

Il ressort de la définition que nous pouvons utiliser un tableau booléen bidimensionnel A pour implémenter la matrice de contiguïté lorsque A[i][j] = true. , cela indique que les sommets i et j sont adjacents. A 来实现邻接矩阵，当 A[i][j] = true 时说明顶点 i 和 j 相邻。

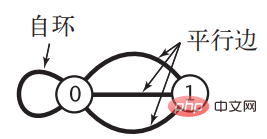
对于 n个顶点的图 G，邻接矩阵需要消耗的空间为 n²个布尔值的大小，对于稀疏图来说会造成很大的浪费，当顶点数很大时所消耗的空间会是个天文数字。同时当图比较特殊，存在自环以及平行边时，邻接矩阵的表示方式是无能为力的。《算法》中给出了存在这两种情况的图：

边的数组

对于无向图，我们可以实现一个类 Edge，里面只用两个实例变量用来存储两个顶点 u和 v，接着在一个数组里面保存所有 Edge

Pour un graphe G avec n sommets, l'espace consommé par la matrice d'adjacence est de n² valeurs booléennes, ce qui entraînera beaucoup de gaspillage pour les graphes clairsemés lorsque le nombre de sommets est grand. , L'espace consommé sera un chiffre astronomique. Dans le même temps, lorsque le graphe est spécial et comporte des boucles automatiques et des arêtes parallèles, la représentation matricielle de contiguïté est impuissante. "Algorithme" donne une image de ces deux situations :

Tableau d'arêtes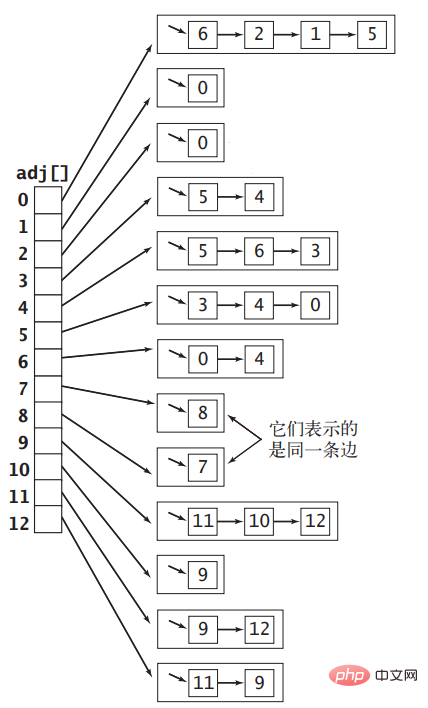

Pour les graphes non orientés, nous pouvons implémenter une classe Edge, qui utilise uniquement deux variables d'instance pour stocker deux sommets u et v , puis tout enregistrer Edge dans un tableau. Il y a un gros problème avec cela, c'est-à-dire que lors de l'obtention de tous les sommets adjacents du sommet v, vous devez parcourir l'ensemble du tableau pour les obtenir. La complexité temporelle est O(|E|). Puisque l'obtention de sommets adjacents est une opération très courante. , Cette façon de l'exprimer ne fonctionne pas non plus.

Tableau de liste d'adjacence

Si nous représentons le sommet comme un entier avec une plage de valeurs de 0∼|V|&moins;1, alors nous pouvons utiliser l'index d'un tableau de longueur |V| pour représenter chaque sommet, puis Chaque élément du tableau est défini comme une liste chaînée, qui contient d'autres sommets adjacents au sommet représenté par l'index. Le graphe non orienté illustré à la figure 1 peut être représenté par le tableau de listes de contiguïté présenté dans la figure ci-dessous :

Le code permettant d'utiliser la liste de contiguïté pour implémenter le graphe non orienté est le suivant, puisque chaque liste chaînée de la liste de contiguïté Le tableau sera enregistré Les sommets adjacents aux sommets, donc lors de l'ajout d'arêtes au graphique, vous devez ajouter des nœuds aux deux listes chaînées du tableau :

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;

/**
 * 使用邻接表实现的无向图
 */
public class LinkGraph implements Graph {
    private final int V;
    private int E;
    private LinkStack<Integer>[] adj;

    public LinkGraph(int V) {
        this.V = V;
        adj = (LinkStack<Integer>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    @Override
    public int V() {
        return V;
    }

    @Override
    public int E() {
        return E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].push(w);
        adj[w].push(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

Le code de pile utilisé ici est le suivant. ne fait pas partie de ce blog Le point clé, donc je ne vais pas trop expliquer ici :

package com.zhiyiyo.collection.stack;

import java.util.EmptyStackException;
import java.util.Iterator;

/**
 * 使用链表实现的堆栈
 */
public class LinkStack<T> {
    private int N;
    private Node first;

    public void push(T item) {
        first = new Node(item, first);
        N++;
    }

    public T pop() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        N--;
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public Iterator<T> iterator() {
        return new ReverseIterator();
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }


    private class ReverseIterator implements Iterator<T> {
        private Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T item = node.item;
            node = node.next;
            return item;
        }

        @Override
        public void remove() {
        }
    }
}

Traversée d'un graphe non orienté

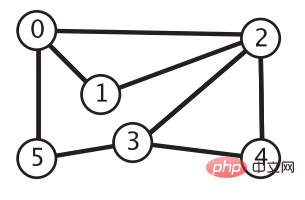
🎜Étant donné l'image suivante, nous devons maintenant trouver le chemin de chaque sommet au sommet 0. Comment faire y parvenir ? Ou pour le dire simplement, étant donné les sommets 0 et 4, il faut déterminer si en partant du sommet 0 peut atteindre le sommet 4. Comment y parvenir ? Cela nécessite l'utilisation de deux méthodes de parcours de graphe : la recherche en profondeur d'abord et la recherche en largeur d'abord. 🎜🎜🎜🎜🎜Avant de présenter ces deux méthodes de traversée, donnons d'abord l'API qui doit être implémentée pour résoudre les problèmes ci-dessus : 🎜

package com.zhiyiyo.graph;

public interface Search {
    /**
     * 起点 s 和 顶点 v 之间是否连通
     * @param v 顶点 v
     * @return 是否连通
     */
    boolean connected(int v);

    /**
     * 返回与顶点 s 相连通的顶点个数（包括 s）
     */
    int count();

    /**
     * 是否存在从起点 s 到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在路径
     */
    boolean hasPathTo(int v);

    /**
     * 从起点 s 到顶点 v 的路径，不存在则返回 null
     * @param v 顶点 v
     * @return 路径
     */
    Iterable<Integer> pathTo(int v);
}

深度优先搜索

深度优先搜索的思想类似树的先序遍历。我们从顶点 0 开始，将它的相邻顶点 2、1、5 加到栈中。接着弹出栈顶的顶点 2，将它相邻的顶点 0、1、3、4 添加到栈中，但是写到这你就会发现一个问题：顶点 0 和 1明明已经在栈中了，如果还把他们加到栈中，那这个栈岂不是永远不会变回空。所以还需要维护一个数组 boolean[] marked，当我们将一个顶点 i 添加到栈中时，就将 marked[i] 置为 true，这样下次要想将顶点 i 加入栈中时，就得先检查一个 marked[i] 是否为 true，如果为 true 就不用再添加了。重复栈顶节点的弹出和节点相邻节点的入栈操作，直到栈为空，我们就完成了顶点 0 可达的所有顶点的遍历。

为了记录每个顶点到顶点 0 的路径，我们还需要一个数组 int[] edgeTo。每当我们访问到顶点 u 并将其一个相邻顶点 i 压入栈中时，就将 edgeTo[i] 设置为 u，说明要想从顶点i 到达顶点 0，需要先回退顶点 u，接着再从顶点 edgeTo[u] 处获取下一步要回退的顶点直至找到顶点 0。

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;


public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public DepthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        dfs();
    }

    /**
     * 递归实现的深度优先搜索
     *
     * @param v 顶点 v
     */
    private void dfs(int v) {
        marked[v] = true;
        N++;
        for (int i : graph.adj(v)) {
            if (!marked[i]) {
                edgeTo[i] = v;
                dfs(i);
            }
        }
    }

    /**
     * 堆栈实现的深度优先搜索
     */
    private void dfs() {
        Stack<Integer> vertexes = new LinkStack<>();
        vertexes.push(s);
        marked[s] = true;

        while (!vertexes.isEmpty()) {
            Integer v = vertexes.pop();
            N++;

            // 将所有相邻顶点加到堆栈中
            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    vertexes.push(i);
                }
            }
        }
    }

    @Override
    public boolean connected(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return N;
    }

    @Override
    public boolean hasPathTo(int v) {
        return connected(v);
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new LinkStack<>();

        int vertex = v;
        while (vertex != s) {
            path.push(vertex);
            vertex = edgeTo[vertex];
        }

        path.push(s);
        return path;
    }
}

广度优先搜索

广度优先搜索的思想类似树的层序遍历。与深度优先搜索不同，从顶点 0 出发，广度优先搜索会先处理完所有与顶点 0 相邻的顶点 2、1、5 后，才会接着处理顶点 2、1、5 的相邻顶点。这个搜索过程就是一圈一圈往外扩展、越走越远的过程，所以可以用来获取顶点 0 到其他节点的最短路径。只要将深度优先搜索中的堆换成队列，就能实现广度优先搜索：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;

public class BreadthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public BreadthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        bfs();
    }

    private void bfs() {
        LinkQueue<Integer> queue = new LinkQueue<>();
        marked[s] = true;
        queue.enqueue(s);

        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            N++;

            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    queue.enqueue(i);
                }
            }
        }
    }
}

队列的实现代码如下：

package com.zhiyiyo.collection.queue;


import java.util.EmptyStackException;


public class LinkQueue<T> {
    private int N;
    private Node first;
    private Node last;

    public void enqueue(T item) {
        Node node = new Node(item, null);
        if (++N == 1) {
            first = node;
        } else {
            last.next = node;
        }
        last = node;
    }

    public T dequeue() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        if (--N == 0) {
            last = null;
        }
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!