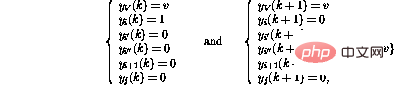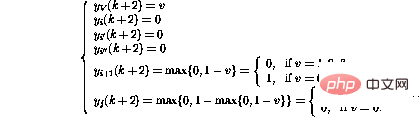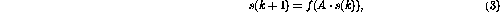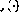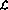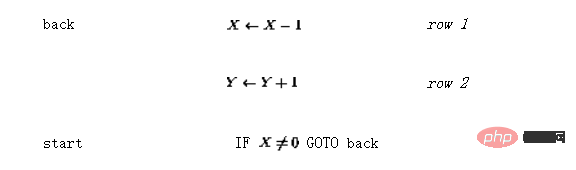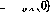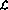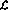Périphériques technologiques
Périphériques technologiques
 IA
IA
 La machine de Turing est le réseau neuronal récurrent le plus populaire en matière d'apprentissage profond ? Le journal de 1996 l'a prouvé !
La machine de Turing est le réseau neuronal récurrent le plus populaire en matière d'apprentissage profond ? Le journal de 1996 l'a prouvé !
La machine de Turing est le réseau neuronal récurrent le plus populaire en matière d'apprentissage profond ? Le journal de 1996 l'a prouvé !
Du 19 au 23 août 1996, la Conférence finlandaise sur l'intelligence artificielle organisée par l'Association finlandaise de l'intelligence artificielle et l'Université de Vaasa s'est tenue à Vaasa, en Finlande.
Un article publié lors de la conférence a prouvé que la machine de Turing est un réseau neuronal récurrent.
Oui, c'était il y a 26 ans !
Jetons un coup d'œil à cet article publié en 1996.
1 Préface
1.1 Classification des réseaux neuronaux
Les réseaux de neurones peuvent être utilisés pour des tâches de classification afin de déterminer si le le modèle d’entrée appartient à des catégories spécifiques.
On sait depuis longtemps que les réseaux feedforward à couche unique ne peuvent être utilisés que pour classer des modèles linéairement séparables, c'est-à-dire que plus il y a de couches consécutives, plus la distribution des classes est élevée. c’est plus complexe.
Lorsque le feedback est introduit dans la structure du réseau, la valeur de sortie du perceptron est recyclée et le nombre de couches consécutives devient en principe infini.
La puissance de calcul a-t-elle été qualitativement améliorée ? La réponse est oui.
Par exemple, un classificateur peut être construit pour déterminer si l'entier d'entrée est premier.
Il s'avère que la taille du réseau utilisé à cet effet peut être finie, et même si la taille entière d'entrée n'est pas limitée, le nombre de nombres premiers qui peuvent être correctement classé est infini.
Dans cet article, "une structure de réseau cyclique composée des mêmes éléments de calcul" peut être utilisée pour compléter n'importe quelle fonction (algorithmiquement) calculable.
1.2 À propos de la calculabilité
Selon les axiomes de base de la théorie de la calculabilité, les machines de Turing peuvent être utilisées pour implémenter des fonctions calculables. Il existe de nombreuses méthodes. peut mettre en œuvre des machines de Turing.
Définir le langage de programmation 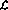 . Le langage comporte quatre opérations de base :
. Le langage comporte quatre opérations de base :

Ici, V représente n'importe quelle variable A. avec une valeur entière positive, j représente n'importe quel numéro de ligne.
On peut montrer que si une fonction est calculable par Turing, elle peut être codée en utilisant ce langage simple (voir [1 pour plus de détails]]) .
2 Réseau de Turing
2.1 Structure du réseau neuronal récursif
Le réseau neuronal étudié dans ce article Composé de perceptrons, ils ont tous la même structure. Le fonctionnement du numéro de perceptron q peut être défini comme
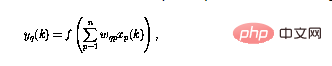
Parmi eux, la sortie du perceptron à l'heure actuelle (représentée par 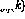 ) utilise l'entrée n #🎜🎜 #Calculé.
) utilise l'entrée n #🎜🎜 #Calculé. 
f peut maintenant être définie comme
#🎜🎜 #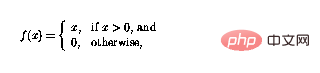 De cette façon, la fonction peut simplement "couper" les valeurs négatives, et les boucles dans le réseau des perceptrons signifient que les perceptrons peuvent être combinés de manière complexe.
De cette façon, la fonction peut simplement "couper" les valeurs négatives, et les boucles dans le réseau des perceptrons signifient que les perceptrons peuvent être combinés de manière complexe.
Figure 1 Le cadre global du réseau neuronal récurrent, la structure est autonome sans apport externe, et le comportement du réseau est entièrement déterminé par l'état initial
Dans la figure 1, la structure récursive est représentée dans un cadre général : maintenant 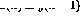 et n sont le nombre de perceptrons, de La connexion de p au perceptron q est représenté par le
et n sont le nombre de perceptrons, de La connexion de p au perceptron q est représenté par le 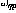 poids scalaire dans (1).
poids scalaire dans (1).
C'est-à-dire que, étant donné un état initial, l'état du réseau itérera jusqu'à ce qu'il ne change plus, et les résultats peuvent être lus à l'état stable ou au « point fixe " du réseau.
2.2 Construction d'un réseau neuronal
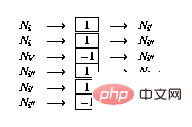
Ensuite, la procédure 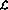 est expliquée ci-dessous réalisée dans. Le réseau est constitué des nœuds (ou perceptrons) suivants :
est expliquée ci-dessous réalisée dans. Le réseau est constitué des nœuds (ou perceptrons) suivants :
-
Pour chaque variable du programme Il y a un nœud variable #🎜🎜 #.
 Pour chaque ligne de programme i
Pour chaque ligne de programme i - , il y a un nœud de commande .
 Pour chaque instruction de branchement conditionnel sur la ligne i
Pour chaque instruction de branchement conditionnel sur la ligne i - , il y a deux nœuds de branchement supplémentaires et #🎜 🎜#.

 Langue
Langue
La mise en œuvre du programme comprend les modifications suivantes au réseau perceptron : #🎜🎜 ##🎜 🎜#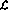 Pour chaque variable V du programme, utilisez le lien suivant pour élargir le réseau :
Pour chaque variable V du programme, utilisez le lien suivant pour élargir le réseau :
- # 🎜🎜# Si la ligne
du code du programme n'a aucune opération ( #🎜 🎜#), puis utilisez le réseau d'augmentation de lien suivant (en supposant que le nœud
#🎜 🎜#), puis utilisez le réseau d'augmentation de lien suivant (en supposant que le nœud
-
 # 🎜🎜#if
# 🎜🎜#if  Si la ligne #i a une opération incrémentale (
Si la ligne #i a une opération incrémentale (
), étendez le réseau comme suit : 
-
S'il y a une opération de décrémentation dans la ligne i (
 ), étendez le réseau comme suit : # 🎜🎜#
), étendez le réseau comme suit : # 🎜🎜#

- Si la ligne i a une branche conditionnelle (# 🎜🎜#), puis élargir le réseau comme suit :

 2.3 Preuve d'équivalence
2.3 Preuve d'équivalence #🎜🎜 #Ce qu'il faut prouver maintenant, c'est que « l'état interne du réseau ou le contenu du nœud du réseau » peut être identifié par l'état du programme, et la continuité de l'état du réseau correspond au flux du programme.
Définir le « statut juridique » du réseau comme suit :
À tous nœuds de transition# La sortie de 🎜🎜#
- et
 (tel que défini en 2.2) est nulle (#🎜🎜 #);
(tel que défini en 2.2) est nulle (#🎜🎜 #); 
 Au plus un nœud de commande
a une sortie unitaire (
Au plus un nœud de commande
a une sortie unitaire ( -
#🎜 🎜#), Tous les autres nœuds d'instruction ont une sortie nulle et
 les nœuds variables ont des valeurs de sortie entières non négatives.
les nœuds variables ont des valeurs de sortie entières non négatives. 
- Si les sorties de tous les nœuds d'instruction sont nulles, l'état est l'état final . Un état légitime du réseau peut être directement interprété comme un "instantané" du programme - si
, le compteur du programme est à la ligne i, Les valeurs des variables correspondantes sont stockées dans des nœuds variables. Les changements d'état du réseau sont activés par des nœuds non nuls.
Tout d'abord, en se concentrant sur les nœuds variables, il s'avère qu'ils se comportent comme des intégrateurs, le contenu précédent du nœud étant renvoyé vers le même nœud.Les seules connexions des nœuds variables vers d'autres nœuds ont des poids négatifs - c'est pourquoi les nœuds contenant des zéros ne changent pas, en raison de la non-linéarité (2).
Ensuite, le nœud d'instruction est expliqué en détail. Supposons que le seul nœud d'instruction non nul
est à l'heurek---cela correspond au compteur du programme à #🎜 dans le code du programme 🎜#i OK. Si la ligne i du programme est
, Ensuite, le comportement du réseau faisant un pas en avant peut être exprimé comme suit (seuls les nœuds concernés sont affichés) 🎜🎜# Il s'avère que le nouvel état du réseau est à nouveau légitime. Par rapport au code du programme, cela correspond au déplacement du compteur du programme vers la ligne i+1.
Par contre, si la iième ligne du programme est
 , le comportement d'un pas en avant est
, le comportement d'un pas en avant est 
De cette façon, en plus de déplacer le compteur du programme à la ligne suivante , la variable V La valeur de diminuera également. Si la ligne i était
 , le fonctionnement du réseau serait le même, sauf que la valeur de la variable V est augmentée.
, le fonctionnement du réseau serait le même, sauf que la valeur de la variable V est augmentée. L'opération de branchement conditionnel (IF GOTO
 j) en ligne i active une séquence d'opérations plus complexe :
j) en ligne i active une séquence d'opérations plus complexe : 
Enfin,

Il s'avère qu'après ces étapes, l'état du réseau peut à nouveau être interprété comme un autre instantané du programme.
La valeur de la variable a changé et le jeton a été transféré au nouvel emplacement, comme si la ligne de programme correspondante était exécutée.
Si le jeton disparaît, l'état du réseau ne change plus - cela ne se produit que lorsque le compteur du programme "dépasse" le code du programme, ce qui signifie que le programme se termine.
Le fonctionnement du réseau est également similaire au fonctionnement du programme correspondant, et la preuve est complète.
3 Modifications
3.1 Extensions
Il est facile de définir des instructions simplifiées supplémentaires qui rendent la programmation plus facile et les programmes résultants plus lisibles et plus rapides à exécuter. Par exemple, la branche inconditionnelle (GOTO j) à la ligne i
de-
peut être implémentée comme
-
en ajoutant la constante c à la variable () à la ligne i peut être Un autre branchement conditionnel (IF V=0 GOTO
j ) en ligne i peut être implémenté comme -
Une instruction d'incrémentation/décrémentation. Supposons que vous vouliez faire ce qui suit :
. Un seul nœud est nécessaire -
:La méthode ci-dessus n'est en aucun cas la seule façon d'implémenter une machine de Turing.
Il s'agit d'une mise en œuvre simple et n'est pas nécessairement optimale dans les applications.
3.2 Formulation matricielle
La construction ci-dessus peut également être mise en œuvre sous la forme d'une matrice.
L'idée de base est de stocker les valeurs des variables et les "compteurs de programme" dans les états de processus s
, et de laisser la matrice de transition d'étatA représenter les liens entre les nœuds.
Le fonctionnement de la structure matricielle peut être défini comme un processus dynamique à temps discret

où la fonction à valeur vectorielle non linéaire
 est maintenant définie élément par élément comme dans (2). Le contenu de la
est maintenant définie élément par élément comme dans (2). Le contenu de la matrice de transition d'étatA est facilement décodé à partir de la formule du réseau - les éléments de la matrice sont les poids entre les nœuds.
Cette formule matricielle est similaire au cadre « matrice conceptuelle » proposé dans [3].
4 Exemple
Supposons que vous souhaitiez implémenter une fonction simple y=x, c'est-à-dire que la valeur de la variable d'entrée x doit être transmise à la variable de sortie y. En utilisant le langage
 , cela peut être codé comme (que le "point d'entrée" ne soit plus la première ligne mais la troisième ligne) :
, cela peut être codé comme (que le "point d'entrée" ne soit plus la première ligne mais la troisième ligne) : 
Le réseau de perceptrons résultant est illustré à la figure 2.
La ligne continue représente une connexion positive (poids 1), et la ligne pointillée représente une connexion négative (poids -1). Par rapport à la figure 1, la structure du réseau est redessinée et simplifiée en intégrant des éléments de retard dans les nœuds.

Figure 2 Implémentation réseau d'un programme simple
Sous forme matricielle, le programme ci-dessus ressemble à
correspond aux deux premières lignes/colonnes de la matrice A En partant du lien vers le nœud représentant les deux variables Y et X, les trois lignes suivantes représentent les trois lignes de programme (1, 2 et 3), et les deux dernières représentent les nœuds supplémentaires requis pour l'instruction de branchement ( 3' et 3'').
Ensuite, il y a les états initial (avant itération) et final (après itération, lorsque le point fixe est trouvé)
Si la valeur du nœud variable sera conservée strictement entre 0 et 1, alors le système dynamique ( 3) L'opération sera linéaire et la fonction n'aura aucun effet.
En principe, la théorie des systèmes linéaires peut alors être utilisée dans l'analyse.
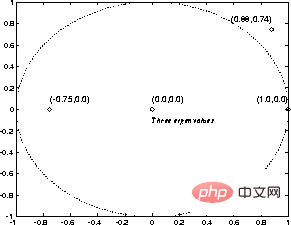
Par exemple, sur la figure 3, les valeurs propres de la matrice de transition d'état A sont représentées.
Même s'il existe des valeurs propres en dehors du cercle unité dans l'exemple ci-dessus, la non-linéarité rend l'itération toujours stable.
Il s'avère que les itérations convergent toujours après
 étapes, où
étapes, où  .
. 
Figure 3 "Valeur propre" d'un programme simple
5 Discussion
5.1 Aspects théoriques
Il s'avère que les machines de Turing peuvent être codées sous forme de réseaux de perceptrons.
Par définition, toutes les fonctions calculables sont calculables par Turing - dans le cadre de la théorie de la calculabilité, il n'existe aucun système informatique plus puissant.
C'est pourquoi, on peut conclure -
Un réseau de perceptrons récurrent (illustré ci-dessus) est (encore une autre) forme de machine de Turing.
L'avantage de cette équivalence est que les résultats de la théorie de la calculabilité sont faciles à obtenir - par exemple, étant donné un réseau et un état initial, il est impossible de dire si le processus finira par s'arrêter.
L'équivalence théorique ci-dessus ne dit rien sur l'efficacité informatique.
Les différents mécanismes qui se produisent dans le réseau peuvent rendre certaines fonctions mieux implémentées dans ce cadre par rapport aux implémentations traditionnelles de machines de Turing (qui sont en fait les ordinateurs d'aujourd'hui).
Au moins dans certains cas, par exemple, une implémentation réseau d'un algorithme peut être parallélisée en autorisant plusieurs "compteurs de programme" dans le vecteur instantané.
Le fonctionnement du réseau est strictement local et non global.
Une question intéressante se pose, par exemple, de savoir si le problème NP-complet peut être attaqué plus efficacement dans un environnement réseau !
Par rapport au langage
 , l'implémentation du réseau a les "extensions" suivantes :
, l'implémentation du réseau a les "extensions" suivantes : -
Les variables peuvent être continues, pas seulement des valeurs entières. En fait, la capacité (théorique) à représenter des nombres réels rend les implémentations de réseaux plus puissantes que le langage
 , dans lequel tous les nombres représentés sont des nombres rationnels.
, dans lequel tous les nombres représentés sont des nombres rationnels.
- Différents « compteurs de programme » peuvent exister en même temps, et le transfert de contrôle peut être « flou », ce qui signifie que la valeur du compteur de programme fournie par le nœud d'instruction peut être non entière.
- Une extension plus petite est un point d'entrée de programme librement définissable. Cela peut aider à simplifier le programme - par exemple, la copie des variables est effectuée dans trois lignes de programme ci-dessus, alors que la solution nominale (voir [1]) nécessite sept lignes et une variable locale supplémentaire.
Par rapport au code du programme original, la formule matricielle est évidemment une représentation d'informations plus "continue" que le code du programme - les paramètres peuvent être modifiés (souvent) et les résultats de l'itération ne changeront pas soudainement.
Cette "redondance" peut être utile dans certaines applications.
Par exemple, lors de l'utilisation d'un algorithme génétique (GA) pour l'optimisation structurelle, la stratégie de recherche aléatoire utilisée dans l'algorithme génétique peut être rendue plus efficace : après la modification de la structure du système, le minimum local de la fonction de coût continu peut être recherché en utilisant une technologie traditionnelle (voir [4]).
En apprenant la structure de la machine à états finis à travers des exemples, comme décrit dans [5], vous pouvez savoir que la méthode d'amélioration itérative de la structure du réseau est également utilisée dans ce cas plus complexe.
Non seulement la théorie des réseaux neuronaux peut bénéficier des résultats ci-dessus - il suffit de regarder la formule du système dynamique (3), il est évident que tous les phénomènes trouvés dans le domaine de la théorie de la calculabilité existent également sous une forme simple - à la recherche de dynamique non linéaire processus.
Par exemple, l'indécidabilité du problème d'arrêt est une contribution intéressante au domaine de la théorie des systèmes : pour tout processus de décision représenté comme une machine de Turing, il existe des systèmes dynamiques de la forme (3) qui violent ce processus - par exemple Construct. un algorithme général d’analyse de stabilité.
5.2 Travaux connexes
Il existe certaines similitudes entre la structure du réseau présentée et le paradigme du réseau neuronal récursif de Hopfield (voir, par exemple, [2]).
Dans les deux cas, "l'entrée" est codée comme l'état initial du réseau, et la "sortie" est lue à partir de l'état final du réseau après des itérations.
Le point fixe du réseau Hopfield est un modèle de modèle préprogrammé, et l'entrée est un modèle de « bruit » - le réseau peut être utilisé pour améliorer les modèles endommagés. Les perspectives (2) de la fonction non linéaire dans
 rendent infini le nombre d'états possibles dans le "réseau de Turing" mentionné ci-dessus.
rendent infini le nombre d'états possibles dans le "réseau de Turing" mentionné ci-dessus. Par rapport au réseau Hopfield où la sortie unitaire est toujours -1 ou 1, on constate qu'en théorie, ces structures de réseau sont très différentes.
Par exemple, alors que l'ensemble des points stables dans un réseau Hopfield est limité, les programmes représentés par les réseaux de Turing ont souvent un nombre illimité de résultats possibles.
Les capacités de calcul des réseaux Hopfield sont discutées dans [6].
Petri net est un outil puissant pour la modélisation de systèmes basés sur des événements et simultanés [7].
Un réseau de Petri est constitué de bits et de transitions et des arcs qui les relient. Chaque endroit peut contenir n'importe quel nombre de jetons, et la distribution des jetons est appelée la marque du réseau de Petri.
Si toutes les positions d'entrée d'une transformation sont occupées par des marqueurs, la transformation peut se déclencher, supprimant un marqueur de chaque emplacement d'entrée et ajoutant un marqueur à chacun de ses emplacements de sortie.
Il peut être prouvé que les réseaux de Petri étendus avec des arcs de suppression supplémentaires ont également les capacités des machines de Turing (voir [7]).
La principale différence entre les réseaux de Turing mentionnés ci-dessus et les réseaux de Petri est que le cadre des réseaux de Petri est plus complexe et a une structure spécialement personnalisée, qui ne peut pas être exprimée par une simple forme générale (3).
Référence
1 Davis, M. et Weyuker, E. : Calculabilité, complexité et langages --- Fondements de l'informatique théorique, New York, 1983.
2 Haykin, S. : Réseaux neuronaux. Une fondation complète. Macmillan College Publishing, New York, 1994.
3 Hyötyniemi, H. : Corrélations --- Éléments constitutifs de l'intelligence ? dimensions de l'intelligence), Société finlandaise d'intelligence artificielle, 1995, pp. 199--226.
4 Hyötyniemi, H. et Koivo, H. : Gènes, codes et systèmes dynamiques dans les actes du deuxième atelier nordique sur. Algorithmes génétiques (NWGA'96), Vaasa, Finlande, 19--23 août 1996.
5 Manolios, P. et Fanelli, R. : Réseaux neuronaux récurrents du premier ordre et automates neuronaux déterministes à états finis 6. , 1994, pp. 1155--1173.
6 Orponen, P. : La puissance de calcul des réseaux Hopfield discrets avec des unités cachées 8, 1996, pp. , J.L. : Théorie des réseaux de Petri et modélisation des systèmes – Prentice--Hall, Englewood Cliffs, New Jersey, 1981.
Références :
https://www.php cn. /lien/0465a1824942fac19824528343613213-
S'il y a une opération de décrémentation dans la ligne i (
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Méthodes et étapes d'utilisation de BERT pour l'analyse des sentiments en Python
Jan 22, 2024 pm 04:24 PM
Méthodes et étapes d'utilisation de BERT pour l'analyse des sentiments en Python
Jan 22, 2024 pm 04:24 PM
BERT est un modèle de langage d'apprentissage profond pré-entraîné proposé par Google en 2018. Le nom complet est BidirectionnelEncoderRepresentationsfromTransformers, qui est basé sur l'architecture Transformer et présente les caractéristiques d'un codage bidirectionnel. Par rapport aux modèles de codage unidirectionnels traditionnels, BERT peut prendre en compte les informations contextuelles en même temps lors du traitement du texte, de sorte qu'il fonctionne bien dans les tâches de traitement du langage naturel. Sa bidirectionnalité permet à BERT de mieux comprendre les relations sémantiques dans les phrases, améliorant ainsi la capacité expressive du modèle. Grâce à des méthodes de pré-formation et de réglage fin, BERT peut être utilisé pour diverses tâches de traitement du langage naturel, telles que l'analyse des sentiments, la dénomination
 Analyse des fonctions d'activation de l'IA couramment utilisées : pratique d'apprentissage en profondeur de Sigmoid, Tanh, ReLU et Softmax
Dec 28, 2023 pm 11:35 PM
Analyse des fonctions d'activation de l'IA couramment utilisées : pratique d'apprentissage en profondeur de Sigmoid, Tanh, ReLU et Softmax
Dec 28, 2023 pm 11:35 PM
Les fonctions d'activation jouent un rôle crucial dans l'apprentissage profond. Elles peuvent introduire des caractéristiques non linéaires dans les réseaux neuronaux, permettant ainsi au réseau de mieux apprendre et simuler des relations entrées-sorties complexes. La sélection et l'utilisation correctes des fonctions d'activation ont un impact important sur les performances et les résultats de formation des réseaux de neurones. Cet article présentera quatre fonctions d'activation couramment utilisées : Sigmoid, Tanh, ReLU et Softmax, à partir de l'introduction, des scénarios d'utilisation, des avantages, Les inconvénients et les solutions d'optimisation sont abordés pour vous fournir une compréhension complète des fonctions d'activation. 1. Fonction sigmoïde Introduction à la formule de la fonction SIgmoïde : La fonction sigmoïde est une fonction non linéaire couramment utilisée qui peut mapper n'importe quel nombre réel entre 0 et 1. Il est généralement utilisé pour unifier le
 Au-delà d'ORB-SLAM3 ! SL-SLAM : les scènes de faible luminosité, de gigue importante et de texture faible sont toutes gérées
May 30, 2024 am 09:35 AM
Au-delà d'ORB-SLAM3 ! SL-SLAM : les scènes de faible luminosité, de gigue importante et de texture faible sont toutes gérées
May 30, 2024 am 09:35 AM
Écrit précédemment, nous discutons aujourd'hui de la manière dont la technologie d'apprentissage profond peut améliorer les performances du SLAM (localisation et cartographie simultanées) basé sur la vision dans des environnements complexes. En combinant des méthodes d'extraction de caractéristiques approfondies et de correspondance de profondeur, nous introduisons ici un système SLAM visuel hybride polyvalent conçu pour améliorer l'adaptation dans des scénarios difficiles tels que des conditions de faible luminosité, un éclairage dynamique, des zones faiblement texturées et une gigue importante. Notre système prend en charge plusieurs modes, notamment les configurations étendues monoculaire, stéréo, monoculaire-inertielle et stéréo-inertielle. En outre, il analyse également comment combiner le SLAM visuel avec des méthodes d’apprentissage profond pour inspirer d’autres recherches. Grâce à des expériences approfondies sur des ensembles de données publiques et des données auto-échantillonnées, nous démontrons la supériorité du SL-SLAM en termes de précision de positionnement et de robustesse du suivi.
 Intégration d'espace latent : explication et démonstration
Jan 22, 2024 pm 05:30 PM
Intégration d'espace latent : explication et démonstration
Jan 22, 2024 pm 05:30 PM
L'intégration d'espace latent (LatentSpaceEmbedding) est le processus de mappage de données de grande dimension vers un espace de faible dimension. Dans le domaine de l'apprentissage automatique et de l'apprentissage profond, l'intégration d'espace latent est généralement un modèle de réseau neuronal qui mappe les données d'entrée de grande dimension dans un ensemble de représentations vectorielles de basse dimension. Cet ensemble de vecteurs est souvent appelé « vecteurs latents » ou « latents ». encodages". Le but de l’intégration de l’espace latent est de capturer les caractéristiques importantes des données et de les représenter sous une forme plus concise et compréhensible. Grâce à l'intégration de l'espace latent, nous pouvons effectuer des opérations telles que la visualisation, la classification et le regroupement de données dans un espace de faible dimension pour mieux comprendre et utiliser les données. L'intégration d'espace latent a de nombreuses applications dans de nombreux domaines, tels que la génération d'images, l'extraction de caractéristiques, la réduction de dimensionnalité, etc. L'intégration de l'espace latent est le principal
 Comprendre en un seul article : les liens et les différences entre l'IA, le machine learning et le deep learning
Mar 02, 2024 am 11:19 AM
Comprendre en un seul article : les liens et les différences entre l'IA, le machine learning et le deep learning
Mar 02, 2024 am 11:19 AM
Dans la vague actuelle de changements technologiques rapides, l'intelligence artificielle (IA), l'apprentissage automatique (ML) et l'apprentissage profond (DL) sont comme des étoiles brillantes, à la tête de la nouvelle vague des technologies de l'information. Ces trois mots apparaissent fréquemment dans diverses discussions de pointe et applications pratiques, mais pour de nombreux explorateurs novices dans ce domaine, leurs significations spécifiques et leurs connexions internes peuvent encore être entourées de mystère. Alors regardons d'abord cette photo. On constate qu’il existe une corrélation étroite et une relation progressive entre l’apprentissage profond, l’apprentissage automatique et l’intelligence artificielle. Le deep learning est un domaine spécifique du machine learning, et le machine learning
 Des bases à la pratique, passez en revue l'historique du développement de la récupération de vecteurs Elasticsearch.
Oct 23, 2023 pm 05:17 PM
Des bases à la pratique, passez en revue l'historique du développement de la récupération de vecteurs Elasticsearch.
Oct 23, 2023 pm 05:17 PM
1. Introduction La récupération de vecteurs est devenue un élément essentiel des systèmes modernes de recherche et de recommandation. Il permet une correspondance de requêtes et des recommandations efficaces en convertissant des objets complexes (tels que du texte, des images ou des sons) en vecteurs numériques et en effectuant des recherches de similarité dans des espaces multidimensionnels. Des bases à la pratique, passez en revue l'historique du développement d'Elasticsearch. vector retrieval_elasticsearch En tant que moteur de recherche open source populaire, le développement d'Elasticsearch en matière de récupération de vecteurs a toujours attiré beaucoup d'attention. Cet article passera en revue l'historique du développement de la récupération de vecteurs Elasticsearch, en se concentrant sur les caractéristiques et la progression de chaque étape. En prenant l'historique comme guide, il est pratique pour chacun d'établir une gamme complète de récupération de vecteurs Elasticsearch.
 Super fort! Top 10 des algorithmes de deep learning !
Mar 15, 2024 pm 03:46 PM
Super fort! Top 10 des algorithmes de deep learning !
Mar 15, 2024 pm 03:46 PM
Près de 20 ans se sont écoulés depuis que le concept d'apprentissage profond a été proposé en 2006. L'apprentissage profond, en tant que révolution dans le domaine de l'intelligence artificielle, a donné naissance à de nombreux algorithmes influents. Alors, selon vous, quels sont les 10 meilleurs algorithmes pour l’apprentissage profond ? Voici les meilleurs algorithmes d’apprentissage profond, à mon avis. Ils occupent tous une position importante en termes d’innovation, de valeur d’application et d’influence. 1. Contexte du réseau neuronal profond (DNN) : Le réseau neuronal profond (DNN), également appelé perceptron multicouche, est l'algorithme d'apprentissage profond le plus courant lorsqu'il a été inventé pour la première fois, jusqu'à récemment en raison du goulot d'étranglement de la puissance de calcul. années, puissance de calcul, La percée est venue avec l'explosion des données. DNN est un modèle de réseau neuronal qui contient plusieurs couches cachées. Dans ce modèle, chaque couche transmet l'entrée à la couche suivante et
 AlphaFold 3 est lancé, prédisant de manière exhaustive les interactions et les structures des protéines et de toutes les molécules de la vie, avec une précision bien plus grande que jamais
Jul 16, 2024 am 12:08 AM
AlphaFold 3 est lancé, prédisant de manière exhaustive les interactions et les structures des protéines et de toutes les molécules de la vie, avec une précision bien plus grande que jamais
Jul 16, 2024 am 12:08 AM
Editeur | Radis Skin Depuis la sortie du puissant AlphaFold2 en 2021, les scientifiques utilisent des modèles de prédiction de la structure des protéines pour cartographier diverses structures protéiques dans les cellules, découvrir des médicaments et dresser une « carte cosmique » de chaque interaction protéique connue. Tout à l'heure, Google DeepMind a publié le modèle AlphaFold3, capable d'effectuer des prédictions de structure conjointe pour des complexes comprenant des protéines, des acides nucléiques, de petites molécules, des ions et des résidus modifiés. La précision d’AlphaFold3 a été considérablement améliorée par rapport à de nombreux outils dédiés dans le passé (interaction protéine-ligand, interaction protéine-acide nucléique, prédiction anticorps-antigène). Cela montre qu’au sein d’un cadre unique et unifié d’apprentissage profond, il est possible de réaliser



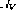 Pour chaque ligne de programme
Pour chaque ligne de programme 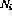 Pour chaque instruction de branchement conditionnel sur la ligne
Pour chaque instruction de branchement conditionnel sur la ligne 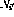
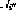 Langue
Langue 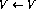 # 🎜🎜#if
# 🎜🎜#if 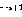 Si la ligne #i
Si la ligne #i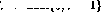 ), étendez le réseau comme suit :
), étendez le réseau comme suit : 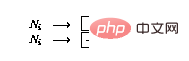

 2.3 Preuve d'équivalence
2.3 Preuve d'équivalence 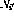 (tel que défini en 2.2) est nulle (#🎜🎜 #);
(tel que défini en 2.2) est nulle (#🎜🎜 #); 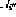
 Au plus un nœud de commande
Au plus un nœud de commande
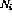 les nœuds variables ont des valeurs de sortie entières non négatives.
les nœuds variables ont des valeurs de sortie entières non négatives. 
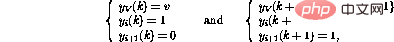
 j
j