 Périphériques technologiques
Périphériques technologiques
 IA
IA
 La méthode d'apprentissage de la représentation causale proposée par Hong Kong et al. vise le problème de généralisation externe de la distribution de données orthographiques complexes.
La méthode d'apprentissage de la représentation causale proposée par Hong Kong et al. vise le problème de généralisation externe de la distribution de données orthographiques complexes.
La méthode d'apprentissage de la représentation causale proposée par Hong Kong et al. vise le problème de généralisation externe de la distribution de données orthographiques complexes.
Avec l'application et la promotion des modèles d'apprentissage en profondeur, les gens ont progressivement découvert que les modèles utilisent souvent de fausses corrélations (Spurious Correlation) dans les données pour obtenir des performances d'entraînement plus élevées. Cependant, comme de telles corrélations ne sont souvent pas vraies sur les données de test, les performances de test de tels modèles sont souvent insatisfaisantes [1]. L'essentiel est que l'objectif traditionnel d'apprentissage automatique (minimisation du risque empirique, ERM) suppose les caractéristiques de distribution indépendantes et identiques de l'ensemble de formation et de test, mais en réalité, les scénarios dans lesquels l'hypothèse de distribution indépendante et identique est vraie sont souvent limités. Dans de nombreux scénarios réels, la distribution des données de formation et la distribution des données de test montrent généralement des incohérences, c'est-à-dire des changements de distribution (Distribution Shifts). Le problème visant à améliorer les performances du modèle dans de tels scénarios est généralement évoqué. problème de généralisation hors distribution (généralisation hors distribution). Une classe de méthodes telles que l'ERM qui se concentrent sur l'apprentissage des corrélations plutôt que sur la causalité dans les données a souvent du mal à gérer les changements de distribution. Bien que de nombreuses méthodes aient émergé ces dernières années et aient fait certains progrès dans le problème de la non-distribution en utilisant le principe d'invariance dans l'inférence causale, la recherche sur les données graphiques est encore limitée. En effet, la généralisation hors distribution des données graphiques est plus difficile que celle des données européennes traditionnelles, ce qui pose davantage de défis à l'apprentissage automatique des graphiques. Cet article prend la tâche de classification des graphes comme exemple pour explorer la généralisation externe de la distribution des graphes basée sur le principe de l'invariance causale.
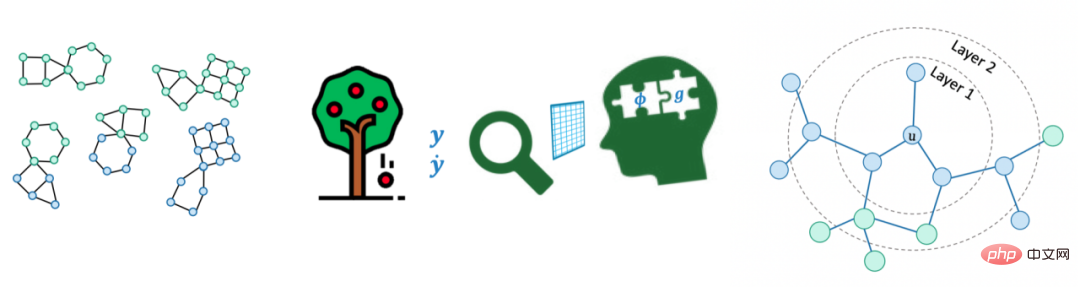
Ces dernières années, grâce au principe d'invariance causale, les gens ont obtenu un certain succès dans le problème de la généralisation hors distribution des données euclidiennes, mais la recherche sur les données graphiques est encore limitée. Contrairement aux données euclidiennes, la complexité des graphiques pose des défis uniques pour l'utilisation des principes d'invariance causale et pour surmonter les difficultés de généralisation hors distribution.
Pour relever ce défi, nous intégrons l'invariance causale dans l'apprentissage automatique des graphes dans ce travail et proposons un cadre d'apprentissage des graphes invariants d'inspiration causale, qui fournit une nouvelle méthode pour résoudre le problème de la généralisation hors distribution des données graphiques. .théories et méthodes.
L'article a été publié dans NeurIPS 2022. Ce travail a été réalisé en coopération avec l'Université chinoise de Hong Kong, l'Université baptiste de Hong Kong, Tencent AI Lab et l'Université de Sydney. Titre de l'article : Apprentissage des représentations causalement invariantes pour la généralisation hors distribution sur les graphiques
 Code du projet : https://github.com/LFhase/CIGA
Code du projet : https://github.com/LFhase/CIGA
- Généralisation hors distribution des données graphiques
- Quelle est la difficulté de la généralisation hors distribution des données graphiques ? Les réseaux de neurones graphiques ont connu un grand succès ces dernières années dans les applications d'apprentissage automatique impliquant des structures graphiques, telles que les systèmes de recommandation, les produits pharmaceutiques assistés par l'IA et d'autres domaines. Cependant, étant donné que la plupart des algorithmes d'apprentissage automatique de graphes existants reposent sur l'hypothèse d'une distribution indépendante et identique des données, lorsque les données de test et les données d'entraînement présentent des décalages (Distribution Shifts), les performances de l'algorithme seront considérablement réduites. Dans le même temps, en raison de la complexité de la structure des données graphiques, la généralisation hors distribution des données graphiques est plus courante et plus difficile que celle des données européennes.
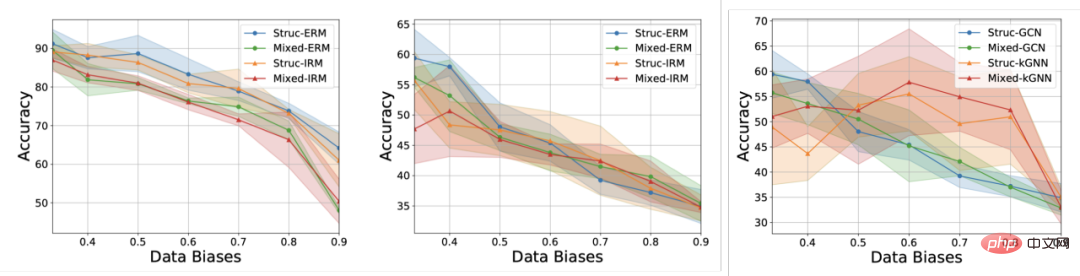
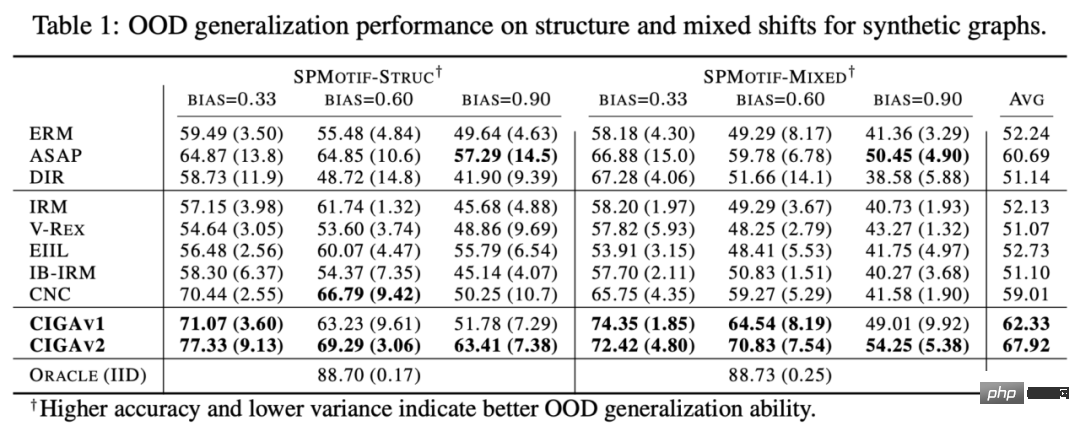
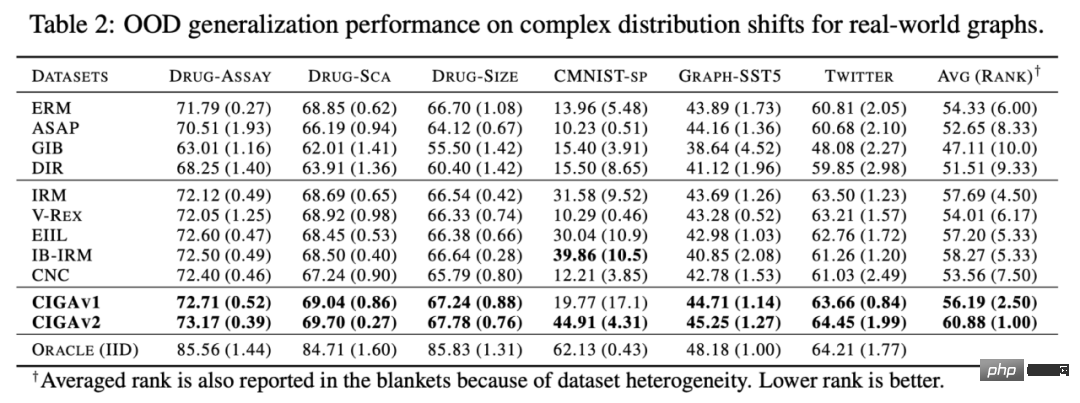
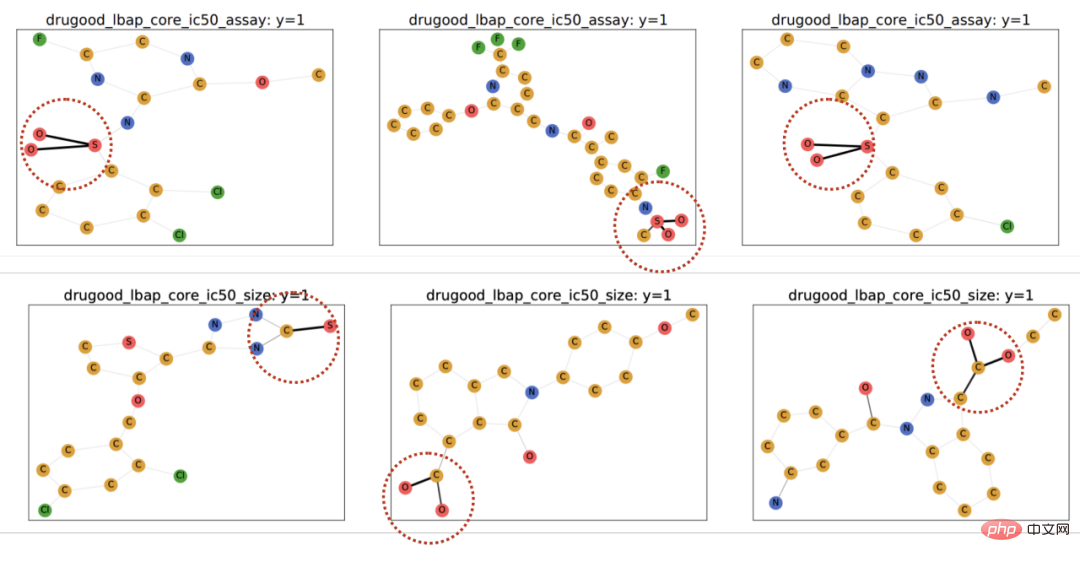
Premièrement, des changements de distribution des données du graphique peuvent apparaître dans la distribution des caractéristiques des nœuds du graphique (décalages au niveau des attributs). Par exemple, dans un système de recommandation, les produits impliqués dans les données de formation peuvent provenir de certaines catégories populaires, et les utilisateurs impliqués peuvent également provenir de certaines régions spécifiques. Cependant, pendant la phase de test, le système doit gérer correctement les utilisateurs de tous. catégories, régions et produits [2,3,4]. De plus, des changements de distribution des données du graphique peuvent également apparaître dans la distribution structurelle du graphique (Structure-level Shifts). Dès 2019, les gens ont remarqué qu'il était difficile d'apprendre aux réseaux de neurones graphiques formés sur des graphiques plus petits des poids d'attention (Attention) efficaces à généraliser à des graphiques plus grands [5], ce qui favorise également une série de travaux connexes ont été proposés [6,7]. Dans des scénarios réels, ces deux types de changements de distribution peuvent souvent apparaître en même temps, et ces changements de distribution à différents niveaux peuvent également présenter différents modèles de fausses corrélations avec les étiquettes à prédire. Par exemple, dans les systèmes de recommandation, les produits de catégories spécifiques et les utilisateurs de régions spécifiques présentent souvent des structures topologiques uniques sur le graphique d'interaction produit-utilisateur [4]. Dans la prédiction des attributs des molécules médicamenteuses, les molécules médicamenteuses impliquées dans la formation peuvent être trop petites et les résultats de la prédiction seront également affectés par l'environnement de mesure expérimental [8]. De plus, la généralisation hors distribution dans l'espace euclidien suppose souvent que les données proviennent de plusieurs environnements (Environnements) ou domaines (Domaine), et suppose en outre que pendant la formation, le modèle peut obtenir l'environnement dans lequel chaque échantillon dans les données de formation appartiennent, afin de découvrir l'invariance entre les environnements. Cependant, l’obtention d’étiquettes environnementales pour les données nécessite souvent certaines connaissances spécialisées liées aux données, et en raison de la nature abstraite des données graphiques, l’obtention d’étiquettes environnementales pour les données graphiques est plus coûteuse. Par conséquent, la plupart des ensembles de données graphiques existants tels que OGB ne contiennent pas de telles informations sur les étiquettes environnementales. Même si quelques ensembles de données, comme DrugOOD, ont des étiquettes environnementales, il existe différents degrés de bruit. Les méthodes existantes peuvent-elles résoudre le problème de la généralisation hors distribution sur les graphes ? Afin d'avoir une compréhension intuitive des défis de la généralisation hors distribution des données graphiques, nous construisons de nouvelles données basées sur l'ensemble de données Spurious-Motif [9] pour instancier davantage les défis ci-dessus, et essayons utiliser des méthodes existantes telles que la cible de formation IRM [10] pour la généralisation hors distribution sur des données européennes, ou GNN [11] avec des capacités d'expression plus fortes, analyser si les méthodes existantes peuvent résoudre le problème de la généralisation hors distribution des données européennes. données graphiques. Figure 2. Exemple d'ensemble de données Spurious Motif. La tâche Spurious Motif est illustrée à la figure 2. Elle juge principalement l'étiquette du graphique en fonction du fait que le graphique d'entrée contient un sous-graphe avec une structure spécifique (telle que Maison ou Cycle), où la couleur du nœud représente le attribut du nœud. L'utilisation de cet ensemble de données peut clairement tester l'impact des changements de distribution à différents niveaux sur les performances des réseaux de neurones graphiques. Pour un modèle GNN ordinaire formé à l'aide d'ERM : De plus, le modèle ne peut obtenir aucune information relative aux labels environnementaux pendant la formation, et les résultats expérimentaux sont présentés dans la figure 3 (plus de résultats peuvent être trouvés dans l'annexe D de l'article). Figure 3. Performances des méthodes existantes sous différents changements de distribution de graphiques. Comme le montre la figure 3, le GCN ordinaire, qu'il soit formé à l'aide d'ERM ou d'IRM, ne peut pas gérer le décalage structurel (Struc) du graphique lors de l'ajout du décalage d'attribut de nœud de graphique (Mixte) et du graphique après la distribution de taille ; est décalé (dans la figure 3), les performances du modèle seront encore réduites ; de plus, même en utilisant kGNN avec une puissance d'expression plus forte, il est difficile d'éviter de graves pertes de performances (performances moyennes réduites ou variance plus grande). De là, nous arrivons naturellement à la question à étudier : Comment obtenir un modèle GNN capable de faire face à divers changements de distribution de graphes ? Afin de résoudre les problèmes ci-dessus, nous devons définir l'objectif d'apprentissage, c'est-à-dire le réseau neuronal du graphe invariant (Invariant GNN), c'est-à-dire qu'il peut toujours fonctionner dans le pire environnement Bon modèle (voir l'article pour une définition rigoureuse) : Définition 1 (réseau neuronal à graphes invariants) Étant donné une série d'ensembles de données de classification de graphes collectés à partir de différents environnements causalement liés , où contient des échantillons indépendants et distribués de manière identique qui sont considérés comme provenant de l'environnement e. Considérons un réseau neuronal graphique , où et sont respectivement l'espace graphique et l'espace échantillon. en entrée, f est un réseau neuronal graphique invariant, si et seulement si , c'est-à-dire minimiser le pire risque empirique dans tous les environnements, où est la perte empirique du modèle dans l'environnement. Le modèle ne peut obtenir qu'une partie des données dans l'environnement de formation pendant la formation Si aucune hypothèse n'est faite sur le processus de données, l'optimalité minmax requise par la définition du réseau neuronal du graphe invariant est difficile à atteindre. réaliser. Par conséquent, nous utilisons un modèle causal structurel pour modéliser le processus de génération de graphiques du point de vue de l'inférence causale et caractériser la corrélation entre les environnements dans le but de définir l'invariance causale sur les données graphiques. Figure 4. Modèle causal du processus de génération de données graphiques. Sans perte de généralité, nous incorporons toutes les variables latentes qui affectent la génération de graphiques dans l'espace latent et modélisons le processus de génération de graphiques comme De plus, C a de nombreux types d'interactions avec Y, S et E dans l'espace latent. Il s'ensuit principalement si la fausse variable latente S et l'étiquette Y ont des associations supplémentaires en plus de la variable latente constante C, c'est-à-dire Sur la base de l'analyse causale ci-dessus, nous pouvons savoir que lorsque le modèle utilise uniquement des sous-graphes invariants pour la prédiction, c'est-à-dire qu'il utilise uniquement la corrélation entre Parmi eux, . Dans de telles conditions, pensez à maximiser En combinant les deux propriétés ci-dessus, nous pouvons déduire Comme il nous est difficile de l'observer directement dans la pratique, nous pouvons l'utiliser comme proxy dans la formule (2) . En même temps, lorsque Parmi eux, a remarqué qu'en maximisant , Figure 5. Schéma du cadre d'apprentissage des graphes invariants d'inspiration causale. Mise en œuvre de CIGA : En pratique, il est souvent difficile d'estimer l'information mutuelle de deux sous-graphes, et l'apprentissage contrastif supervisé [ 11 ] propose une solution réalisable : où Dans les expériences, nous avons utilisé 16 ensembles de données synthétiques ou réels pour valider pleinement CIGA sous différents changements de distribution graphique. Dans l'expérience, nous avons implémenté le prototype de CIGA en utilisant le framework GNN interprétable [9], mais en fait CIGA a plus de moyens de l'implémenter. Pour des ensembles de données spécifiques et des détails expérimentaux, veuillez consulter la section expérimentale de l'article. Performance du changement de distribution de structure et du changement de distribution mixte dans l'ensemble de données synthétiques Nous avons d'abord construit des ensembles de données SPMotif-Struc et SPMotif-Mixed basés sur l'ensemble de données SPMotif [9], où SPMotif-Struc inclut de fausses corrélations entre des sous-graphiques spécifiques et d'autres structures de sous-graphiques dans le graphique, ainsi que des décalages de distribution des tailles de graphique tandis que SPMotif-Mixed ajoute des décalages de distribution au niveau des attributs du nœud du graphique en fonction de SPMotif-Struc. La première colonne du tableau est la base de référence de l'ERM et du GNN interprétable, et la deuxième colonne est l'algorithme de généralisation hors distribution le plus avancé dans l'espace euclidien. Les résultats montrent que le meilleur cadre GNN et l'algorithme de généralisation hors distribution dans l'espace euclidien sont soumis aux changements de distribution sur le graphique, et que lorsque davantage de changements de distribution se produisent, la perte de performance (performance de classification moyenne plus faible ou une plus grande variance) sera encore améliorée. En revanche, CIGA maintient de bonnes performances sous des changements de distribution de différentes forces et dépasse largement les meilleures performances de base. Performance de divers changements de distribution de graphiques sur des ensembles de données réels Nous avons ensuite testé les performances de CIGA sur des ensembles de données réels et des changements de distribution de graphiques qui existent dans diverses données réelles. Il comprend trois données. ensembles de trois divisions d'environnement différentes (analyse de l'environnement expérimental, échafaudage du squelette moléculaire et taille moléculaire) dans DrugOOD pour la prédiction des attributs des molécules médicamenteuses assistée par l'IA dans les produits pharmaceutiques assistés par l'IA, y compris les changements de distribution des graphiques dans divers scénarios d'application réels ; converti sur la base de l'ensemble de données d'image classique ColoredMNIST [10] dans l'espace euclidien comprend principalement le décalage de distribution de type PIIF des attributs de nœud graphique ; le Graph-SST5 et Twitter convertis sur la base de l'ensemble de données de classification des émotions en langage naturel SST5 et Twitter [15], et a également ajouté un changement de distribution du degré du graphique. De plus, nous avons également utilisé 4 ensembles de données de décalage de distribution de taille de graphe moléculaire précédemment étudiés [7], Les résultats des tests sont présentés dans le tableau ci-dessus. On constate que dans les données réelles, en raison de l'augmentation de la difficulté de la tâche, les performances du modèle obtenues en utilisant un GNN mieux architecturé ou hors de. -La formation des cibles d'optimisation de généralisation de distribution dans l'espace euclidien est encore plus faible que le modèle GNN ordinaire formé à l'aide d'ERM. Ce phénomène est également similaire au phénomène observé dans les expériences de généralisation hors distribution sous des tâches plus difficiles dans l'espace euclidien [16], reflétant la difficulté de la généralisation hors distribution sur des données réelles et les lacunes des méthodes existantes. En revanche, CIGA peut améliorer tous les changements de distribution de données et de graphiques réels, et même atteindre le niveau Oracle empiriquement optimal dans certains ensembles de données tels que Twitter et PROTEINS. Des tests préliminaires sur le dernier test de référence de test de généralisation de graphiques hors distribution BON sur l'ensemble de données de classification de graphiques montrent également que CIGA est actuellement le meilleur algorithme de généralisation de graphiques hors distribution capable de faire face à divers changements de distribution de graphiques. En raison de l'utilisation de GNN interprétables comme architecture de mise en œuvre du prototype de CIGA, nous avons également visualisé le DrugOOD identifié par le modèle et avons constaté que CIGA a trouvé des groupes moléculaires relativement cohérents pour la prédiction des attributs moléculaires. Cela peut fournir une meilleure base pour les produits pharmaceutiques ultérieurs assistés par l’IA. Figure 6. Sous-graphe partiellement invariant identifié par CIGA dans DrugOOD. À travers la perspective de l'inférence causale, cet article introduit pour la première fois l'invariance causale au problème de distribution de graphes hors généralisation sous divers changements de distribution de graphes, et propose une nouvelle solution théoriquement garantie le cadre CIGA. Un grand nombre d'expériences ont également pleinement vérifié les excellentes performances de généralisation hors distribution de CIGA. En regardant vers l'avenir, sur la base de CIGA, nous pouvons explorer davantage de meilleurs cadres de mise en œuvre [17], ou introduire de meilleures méthodes d'amélioration des données théoriquement garanties pour CIGA [3,18], et modéliser théoriquement l'association sur le graphique (décalage variable). ) [19] pour améliorer encore la capacité du CIGA à identifier les sous-graphes invariants et promouvoir la mise en œuvre réelle de réseaux neuronaux graphiques dans des scénarios d'application réels tels que les produits pharmaceutiques assistés par l'IA. 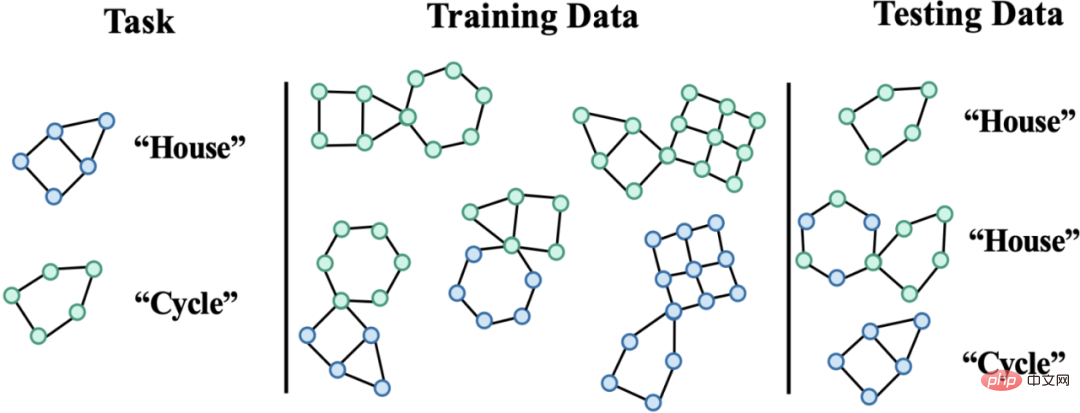
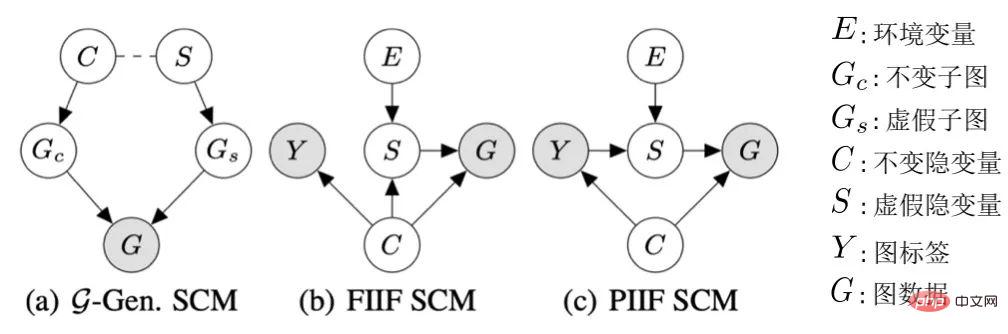
Modèle causal pour la généralisation en dehors de la distribution de données graphiques
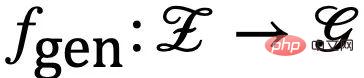 . De plus, pour la variable latente
. De plus, pour la variable latente  , selon qu'elle est affectée ou non par l'environnement E, on la divise en une variable latente invariante (variable latente invariante)
, selon qu'elle est affectée ou non par l'environnement E, on la divise en une variable latente invariante (variable latente invariante)  et une variable latente parasite (variable latente parasite)
et une variable latente parasite (variable latente parasite) 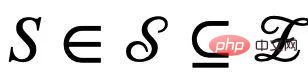 . De manière correspondante, les variables latentes C et S affecteront respectivement la génération d'un certain sous-graphe de G, qui sont respectivement enregistrés comme le sous-graphe invariant
. De manière correspondante, les variables latentes C et S affecteront respectivement la génération d'un certain sous-graphe de G, qui sont respectivement enregistrés comme le sous-graphe invariant  et le faux sous-graphe
et le faux sous-graphe  , comme le montre la figure 4 (a), et C contrôle principalement l'étiquette Y du graphique. Cela peut également être dérivé davantage
, comme le montre la figure 4 (a), et C contrôle principalement l'étiquette Y du graphique. Cela peut également être dérivé davantage 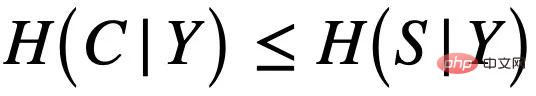 , c'est-à-dire que C et Y ont des informations mutuelles plus élevées que S. Ce processus de génération correspond à de nombreux exemples pratiques. Par exemple, les propriétés médicinales d'une molécule sont généralement déterminées par un certain groupe clé (sous-graphe moléculaire) (comme la solubilité dans l'eau de l'hydroxyle-HO par rapport à la molécule).
, c'est-à-dire que C et Y ont des informations mutuelles plus élevées que S. Ce processus de génération correspond à de nombreux exemples pratiques. Par exemple, les propriétés médicinales d'une molécule sont généralement déterminées par un certain groupe clé (sous-graphe moléculaire) (comme la solubilité dans l'eau de l'hydroxyle-HO par rapport à la molécule).  , Il peut être résumé en deux types : FIIF (Fonction invariante entièrement informative) comme le montre la figure 4 (b) et PIIF (Fonction invariante partiellement informative) comme le montre la figure 4 (c). Parmi eux, FIIF signifie que l'étiquette est indépendante du montant de fausse corrélation étant donné les informations invariantes. PIIF est le contraire. Il convient de noter que afin de couvrir autant de changements de distribution de graphiques que possible, notre modèle causal s'efforce de modéliser largement divers modèles de génération de graphiques. Étant donné plus de connaissances sur le processus de génération de graphiques, le modèle causal présenté dans la figure 4 peut être généralisé à des exemples plus spécifiques. Comme dans l'Annexe C.1, nous montrons comment les graphes causals peuvent être généralisés aux travaux antérieurs de Bevilacqua et al. [7] sur l'analyse des changements de distribution de la taille des graphes en ajoutant l'hypothèse d'une limite de graphe supplémentaire (graphon).
, Il peut être résumé en deux types : FIIF (Fonction invariante entièrement informative) comme le montre la figure 4 (b) et PIIF (Fonction invariante partiellement informative) comme le montre la figure 4 (c). Parmi eux, FIIF signifie que l'étiquette est indépendante du montant de fausse corrélation étant donné les informations invariantes. PIIF est le contraire. Il convient de noter que afin de couvrir autant de changements de distribution de graphiques que possible, notre modèle causal s'efforce de modéliser largement divers modèles de génération de graphiques. Étant donné plus de connaissances sur le processus de génération de graphiques, le modèle causal présenté dans la figure 4 peut être généralisé à des exemples plus spécifiques. Comme dans l'Annexe C.1, nous montrons comment les graphes causals peuvent être généralisés aux travaux antérieurs de Bevilacqua et al. [7] sur l'analyse des changements de distribution de la taille des graphes en ajoutant l'hypothèse d'une limite de graphe supplémentaire (graphon). 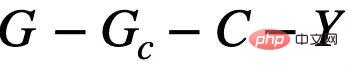 , la prédiction du modèle ne sera pas affectée par les changements dans le environnement E Impact ; Au contraire, si la prédiction du modèle repose sur des informations liées à S ou
, la prédiction du modèle ne sera pas affectée par les changements dans le environnement E Impact ; Au contraire, si la prédiction du modèle repose sur des informations liées à S ou  , ses résultats de prédiction seront considérablement modifiés en raison du changement de E, entraînant une perte de performances. Par conséquent, notre objectif peut être affiné davantage depuis l'apprentissage d'un réseau neuronal à graphes invariants pour : a) identifier des sous-graphes invariants potentiels b) prédire Y à l'aide des sous-graphes identifiés ; Afin de mieux correspondre au processus algorithmique de génération de données, nous divisons en outre le réseau neuronal du graphe en un réseau de reconnaissance de sous-graphes (Featurizer GNN)
, ses résultats de prédiction seront considérablement modifiés en raison du changement de E, entraînant une perte de performances. Par conséquent, notre objectif peut être affiné davantage depuis l'apprentissage d'un réseau neuronal à graphes invariants pour : a) identifier des sous-graphes invariants potentiels b) prédire Y à l'aide des sous-graphes identifiés ; Afin de mieux correspondre au processus algorithmique de génération de données, nous divisons en outre le réseau neuronal du graphe en un réseau de reconnaissance de sous-graphes (Featurizer GNN)  et un réseau de classification (Classifier GNN)
et un réseau de classification (Classifier GNN) 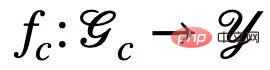 , et
, et 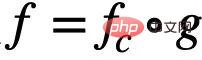 , où
, où  est l'espace sous-graphe de
est l'espace sous-graphe de  . Ensuite, l'objectif d'apprentissage du modèle peut être exprimé comme indiqué dans la formule (1) :
. Ensuite, l'objectif d'apprentissage du modèle peut être exprimé comme indiqué dans la formule (1) : 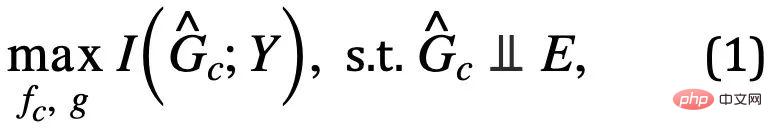
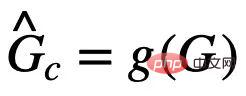 est la prédiction du sous-graphe invariant par le réseau de reconnaissance de sous-graphes
est la prédiction du sous-graphe invariant par le réseau de reconnaissance de sous-graphes  est # ; 🎜🎜#
est # ; 🎜🎜# les informations mutuelles avec Y, généralement, en maximisant
les informations mutuelles avec Y, généralement, en maximisant 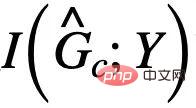 peuvent être utilisées en minimisant
peuvent être utilisées en minimisant  Prédire le réalisation empirique des pertes de Y. Cependant, en raison du manque de E, il nous est difficile d'utiliser directement E pour vérifier l'indépendance de
Prédire le réalisation empirique des pertes de Y. Cependant, en raison du manque de E, il nous est difficile d'utiliser directement E pour vérifier l'indépendance de  . À cette fin, nous devons rechercher d'autres conditions d'équivalence pour identifier l'invariant requis. sous-graphiques.
. À cette fin, nous devons rechercher d'autres conditions d'équivalence pour identifier l'invariant requis. sous-graphiques. 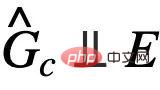 Apprentissage de graphes invariants d'inspiration causale
Apprentissage de graphes invariants d'inspiration causale 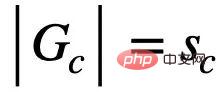 , bien que
, bien que 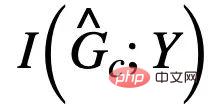 ait le même effet que
ait le même effet que  Le taille du sous-graphe invariant estimé contient de faux sous-graphes qui ont des informations mutuelles avec Y.
Le taille du sous-graphe invariant estimé contient de faux sous-graphes qui ont des informations mutuelles avec Y.  Afin d'"éliminer" les éventuels faux sous-graphes dans
Afin d'"éliminer" les éventuels faux sous-graphes dans  , nous rechercherons davantage à partir du modèle causal Plus sur les attributs uniques de
, nous rechercherons davantage à partir du modèle causal Plus sur les attributs uniques de 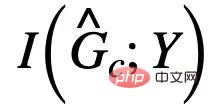 . Notez que, quel que soit le type de fausse corrélation PIIF ou FIIF, pour le sous-graphe qui maximise les informations mutuelles avec l'étiquette Y, nous avons :
. Notez que, quel que soit le type de fausse corrélation PIIF ou FIIF, pour le sous-graphe qui maximise les informations mutuelles avec l'étiquette Y, nous avons :
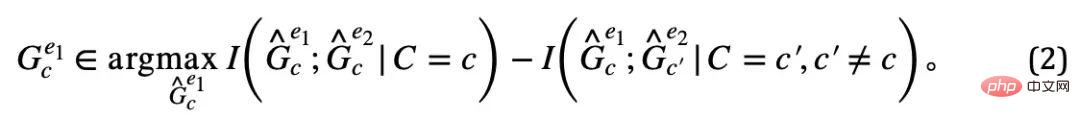
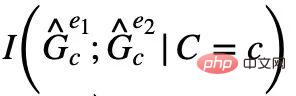 et
et 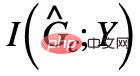 sont maximisés en même temps,
sont maximisés en même temps, 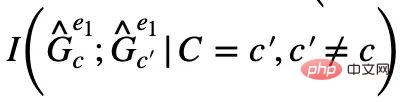 sera automatiquement minimisé, sinon les prédictions du modèle s'effondreront en une solution triviale. À partir de là, nous avons obtenu la condition d'équivalence de sous-graphe invariant dans un cas simple. En combinaison avec la formule (1), nous avons obtenu la première version du cadre d'apprentissage de graphe invariant inspiré de la causalité (apprentissage de graphe invariant inspiré de la causalité), à savoir CIGAv1 :
sera automatiquement minimisé, sinon les prédictions du modèle s'effondreront en une solution triviale. À partir de là, nous avons obtenu la condition d'équivalence de sous-graphe invariant dans un cas simple. En combinaison avec la formule (1), nous avons obtenu la première version du cadre d'apprentissage de graphe invariant inspiré de la causalité (apprentissage de graphe invariant inspiré de la causalité), à savoir CIGAv1 : 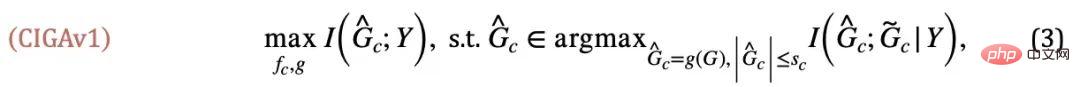
 et
et  , soit
, soit  et G sont issus de la même catégorie Y. Dans notre article, nous démontrons en outre que CIGAv1 peut identifier avec succès des sous-graphes invariants potentiels dans le modèle causal correspondant à la figure 4 lorsque la taille du graphique est connue. Cependant, comme les hypothèses précédentes sont trop idéales, en pratique, la taille du sous-graphe invariant peut changer et la taille correspondante est souvent inconnue. En supposant qu'il n'y ait pas de taille de sous-graphe, les exigences CIGAv1 peuvent être satisfaites en identifiant simplement le graphe entier comme un sous-graphe invariant. Par conséquent, nous envisageons de rechercher davantage de propriétés sur les sous-graphes invariants pour supprimer cette hypothèse.
et G sont issus de la même catégorie Y. Dans notre article, nous démontrons en outre que CIGAv1 peut identifier avec succès des sous-graphes invariants potentiels dans le modèle causal correspondant à la figure 4 lorsque la taille du graphique est connue. Cependant, comme les hypothèses précédentes sont trop idéales, en pratique, la taille du sous-graphe invariant peut changer et la taille correspondante est souvent inconnue. En supposant qu'il n'y ait pas de taille de sous-graphe, les exigences CIGAv1 peuvent être satisfaites en identifiant simplement le graphe entier comme un sous-graphe invariant. Par conséquent, nous envisageons de rechercher davantage de propriétés sur les sous-graphes invariants pour supprimer cette hypothèse. 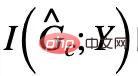 peut apparaître #🎜🎜 ##🎜 🎜#
peut apparaître #🎜🎜 ##🎜 🎜#  est supprimée Partage de parties de sous-graphe invariant les mêmes informations mutuelles et associées. Alors, pouvons-nous faire le contraire et maximiser pour supprimer d'éventuelles fausses intrigues secondaires de
est supprimée Partage de parties de sous-graphe invariant les mêmes informations mutuelles et associées. Alors, pouvons-nous faire le contraire et maximiser pour supprimer d'éventuelles fausses intrigues secondaires de 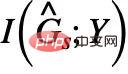 ? La réponse est oui, on peut utiliser la corrélation entre
? La réponse est oui, on peut utiliser la corrélation entre  et Y pour la faire concurrencer l'estimation de
et Y pour la faire concurrencer l'estimation de  . Il convient de noter que lors de la maximisation de
. Il convient de noter que lors de la maximisation de  , vous devez vous assurer que
, vous devez vous assurer que 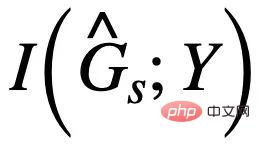 ne dépassera pas
ne dépassera pas 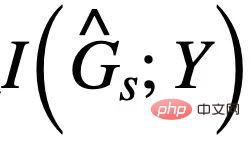 #🎜 🎜# , sinon prédira
#🎜 🎜# , sinon prédira 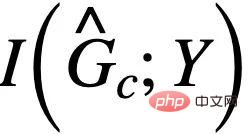 et tombera dans une solution triviale. Combiné avec cette condition supplémentaire, nous pouvons supprimer l'hypothèse sur la taille constante du sous-graphe de la formule (3) et obtenir le CIGAv2 suivant : #
et tombera dans une solution triviale. Combiné avec cette condition supplémentaire, nous pouvons supprimer l'hypothèse sur la taille constante du sous-graphe de la formule (3) et obtenir le CIGAv2 suivant : #
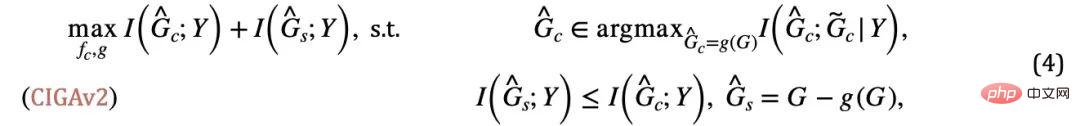
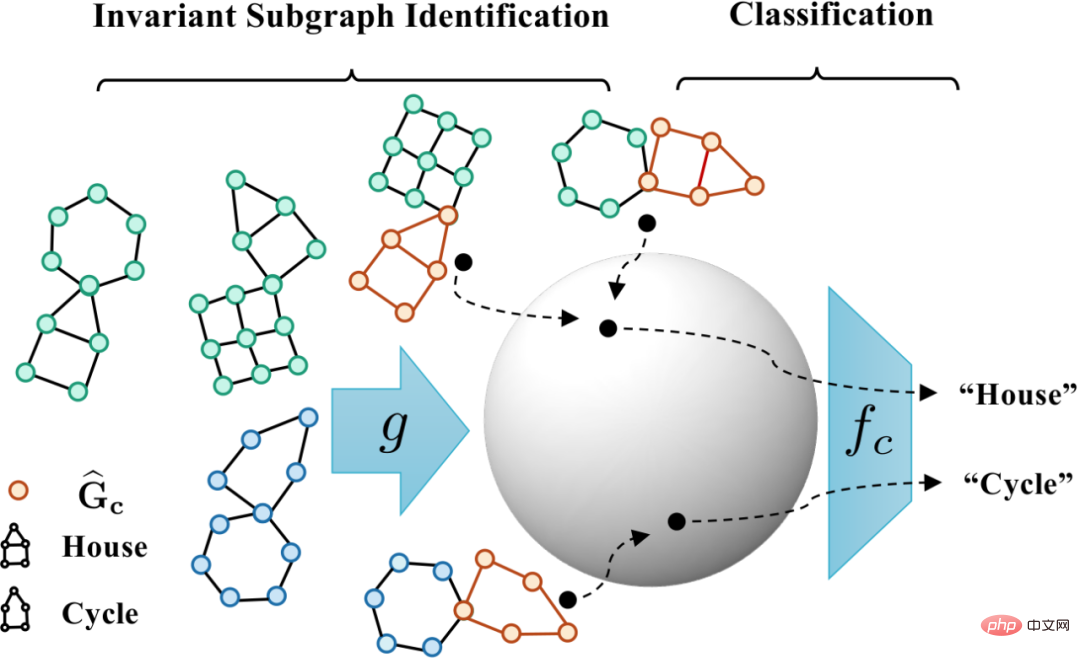
 correspond à l'échantillon positif dans la formule (4), et
correspond à l'échantillon positif dans la formule (4), et 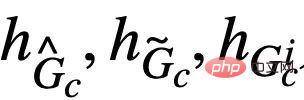 est la représentation graphique correspondant à
est la représentation graphique correspondant à 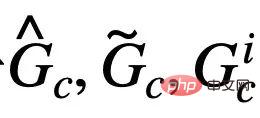 . Lorsque
. Lorsque  , la formule (5) fournit un estimateur d'entropie de resubstituation non paramétrique (estimateur d'entropie de resubstituation non paramétrique) basé sur la densité du noyau de von Mises-Fisher pour
, la formule (5) fournit un estimateur d'entropie de resubstituation non paramétrique (estimateur d'entropie de resubstituation non paramétrique) basé sur la densité du noyau de von Mises-Fisher pour 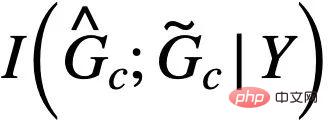 [13,14]. La mise en œuvre finale de la partie centrale de CIGA est illustrée à la figure 5, c'est-à-dire en rapprochant la représentation graphique de la même catégorie de sous-graphes invariants dans l'espace de représentation latente, et en maximisant en même temps la représentation graphique des différentes catégories de sous-graphes invariants. sous-graphes invariants pour maximiser
[13,14]. La mise en œuvre finale de la partie centrale de CIGA est illustrée à la figure 5, c'est-à-dire en rapprochant la représentation graphique de la même catégorie de sous-graphes invariants dans l'espace de représentation latente, et en maximisant en même temps la représentation graphique des différentes catégories de sous-graphes invariants. sous-graphes invariants pour maximiser 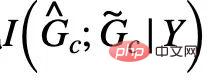 . De plus, pour une autre contrainte dans la formule (4), nous pouvons l'implémenter grâce à l'idée de perte charnière, c'est-à-dire
. De plus, pour une autre contrainte dans la formule (4), nous pouvons l'implémenter grâce à l'idée de perte charnière, c'est-à-dire 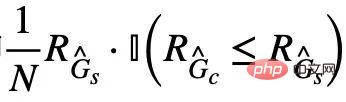 , qui optimise uniquement les faux sous-graphes dont la perte empirique lors de la prédiction est supérieure au sous-graphe invariant correspondant.
, qui optimise uniquement les faux sous-graphes dont la perte empirique lors de la prédiction est supérieure au sous-graphe invariant correspondant. Expériences et discussions

Résumé et perspectives
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1393
1393
 52
52
 1207
1207
 24
24
 Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
À la pointe de la technologie logicielle, le groupe de l'UIUC Zhang Lingming, en collaboration avec des chercheurs de l'organisation BigCode, a récemment annoncé le modèle de grand code StarCoder2-15B-Instruct. Cette réalisation innovante a permis une percée significative dans les tâches de génération de code, dépassant avec succès CodeLlama-70B-Instruct et atteignant le sommet de la liste des performances de génération de code. Le caractère unique de StarCoder2-15B-Instruct réside dans sa stratégie d'auto-alignement pur. L'ensemble du processus de formation est ouvert, transparent et complètement autonome et contrôlable. Le modèle génère des milliers d'instructions via StarCoder2-15B en réponse au réglage fin du modèle de base StarCoder-15B sans recourir à des annotations manuelles coûteuses.
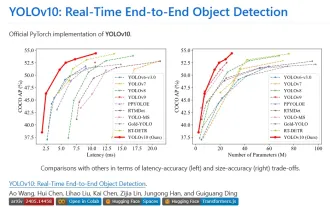 Yolov10 : explication détaillée, déploiement et application en un seul endroit !
Jun 07, 2024 pm 12:05 PM
Yolov10 : explication détaillée, déploiement et application en un seul endroit !
Jun 07, 2024 pm 12:05 PM
1. Introduction Au cours des dernières années, les YOLO sont devenus le paradigme dominant dans le domaine de la détection d'objets en temps réel en raison de leur équilibre efficace entre le coût de calcul et les performances de détection. Les chercheurs ont exploré la conception architecturale de YOLO, les objectifs d'optimisation, les stratégies d'expansion des données, etc., et ont réalisé des progrès significatifs. Dans le même temps, le recours à la suppression non maximale (NMS) pour le post-traitement entrave le déploiement de bout en bout de YOLO et affecte négativement la latence d'inférence. Dans les YOLO, la conception de divers composants manque d’une inspection complète et approfondie, ce qui entraîne une redondance informatique importante et limite les capacités du modèle. Il offre une efficacité sous-optimale et un potentiel d’amélioration des performances relativement important. Dans ce travail, l'objectif est d'améliorer encore les limites d'efficacité des performances de YOLO à la fois en post-traitement et en architecture de modèle. à cette fin
 L'Université Tsinghua a pris le relais et YOLOv10 est sorti : les performances ont été grandement améliorées et il figurait sur la hot list de GitHub
Jun 06, 2024 pm 12:20 PM
L'Université Tsinghua a pris le relais et YOLOv10 est sorti : les performances ont été grandement améliorées et il figurait sur la hot list de GitHub
Jun 06, 2024 pm 12:20 PM
La série de référence YOLO de systèmes de détection de cibles a une fois de plus reçu une mise à niveau majeure. Depuis la sortie de YOLOv9 en février de cette année, le relais de la série YOLO (YouOnlyLookOnce) a été passé entre les mains de chercheurs de l'Université Tsinghua. Le week-end dernier, la nouvelle du lancement de YOLOv10 a attiré l'attention de la communauté IA. Il est considéré comme un cadre révolutionnaire dans le domaine de la vision par ordinateur et est connu pour ses capacités de détection d'objets de bout en bout en temps réel, poursuivant l'héritage de la série YOLO en fournissant une solution puissante alliant efficacité et précision. Adresse de l'article : https://arxiv.org/pdf/2405.14458 Adresse du projet : https://github.com/THU-MIG/yo
 Comment évaluer la rentabilité du support commercial des frameworks Java
Jun 05, 2024 pm 05:25 PM
Comment évaluer la rentabilité du support commercial des frameworks Java
Jun 05, 2024 pm 05:25 PM
L'évaluation du rapport coût/performance du support commercial pour un framework Java implique les étapes suivantes : Déterminer le niveau d'assurance requis et les garanties de l'accord de niveau de service (SLA). L’expérience et l’expertise de l’équipe d’appui à la recherche. Envisagez des services supplémentaires tels que les mises à niveau, le dépannage et l'optimisation des performances. Évaluez les coûts de support commercial par rapport à l’atténuation des risques et à une efficacité accrue.
 Rapport technique Google Gemini 1.5 : prouvez facilement les questions de l'Olympiade mathématique, la version Flash est 5 fois plus rapide que GPT-4 Turbo
Jun 13, 2024 pm 01:52 PM
Rapport technique Google Gemini 1.5 : prouvez facilement les questions de l'Olympiade mathématique, la version Flash est 5 fois plus rapide que GPT-4 Turbo
Jun 13, 2024 pm 01:52 PM
En février de cette année, Google a lancé le grand modèle multimodal Gemini 1.5, qui a considérablement amélioré les performances et la vitesse grâce à l'ingénierie et à l'optimisation de l'infrastructure, à l'architecture MoE et à d'autres stratégies. Avec un contexte plus long, des capacités de raisonnement plus fortes et une meilleure gestion du contenu multimodal. Ce vendredi, Google DeepMind a officiellement publié le rapport technique de Gemini 1.5, qui couvre la version Flash et d'autres mises à jour récentes. Le document fait 153 pages. Lien du rapport technique : https://storage.googleapis.com/deepmind-media/gemini/gemini_v1_5_report.pdf Dans ce rapport, Google présente Gemini1
 Revoir! Résumer de manière exhaustive le rôle important des modèles de base dans la promotion de la conduite autonome
Jun 11, 2024 pm 05:29 PM
Revoir! Résumer de manière exhaustive le rôle important des modèles de base dans la promotion de la conduite autonome
Jun 11, 2024 pm 05:29 PM
Écrit ci-dessus et compréhension personnelle de l'auteur : Récemment, avec le développement et les percées de la technologie d'apprentissage profond, les modèles de base à grande échelle (Foundation Models) ont obtenu des résultats significatifs dans les domaines du traitement du langage naturel et de la vision par ordinateur. L’application de modèles de base à la conduite autonome présente également de grandes perspectives de développement, susceptibles d’améliorer la compréhension et le raisonnement des scénarios. Grâce à une pré-formation sur un langage riche et des données visuelles, le modèle de base peut comprendre et interpréter divers éléments des scénarios de conduite autonome et effectuer un raisonnement, fournissant ainsi un langage et des commandes d'action pour piloter la prise de décision et la planification. Le modèle de base peut être constitué de données enrichies d'une compréhension du scénario de conduite afin de fournir les rares caractéristiques réalisables dans les distributions à longue traîne qui sont peu susceptibles d'être rencontrées lors d'une conduite de routine et d'une collecte de données.
 Comment les options légères des frameworks PHP affectent-elles les performances des applications ?
Jun 06, 2024 am 10:53 AM
Comment les options légères des frameworks PHP affectent-elles les performances des applications ?
Jun 06, 2024 am 10:53 AM
Le framework PHP léger améliore les performances des applications grâce à une petite taille et une faible consommation de ressources. Ses fonctionnalités incluent : une petite taille, un démarrage rapide, une faible utilisation de la mémoire, une vitesse de réponse et un débit améliorés et une consommation de ressources réduite. Cas pratique : SlimFramework crée une API REST, seulement 500 Ko, une réactivité élevée et un débit élevé.
 Comment la courbe d'apprentissage des frameworks PHP se compare-t-elle à celle d'autres frameworks de langage ?
Jun 06, 2024 pm 12:41 PM
Comment la courbe d'apprentissage des frameworks PHP se compare-t-elle à celle d'autres frameworks de langage ?
Jun 06, 2024 pm 12:41 PM
La courbe d'apprentissage d'un framework PHP dépend de la maîtrise du langage, de la complexité du framework, de la qualité de la documentation et du support de la communauté. La courbe d'apprentissage des frameworks PHP est plus élevée par rapport aux frameworks Python et inférieure par rapport aux frameworks Ruby. Par rapport aux frameworks Java, les frameworks PHP ont une courbe d'apprentissage modérée mais un temps de démarrage plus court.



