Quelle est la méthode d'implémentation de l'algorithme KMP en Java ?

illustration

l'algorithme kmp présente certaines similitudes avec l'idée de l'algorithme bm évoquée précédemment. Comme mentionné précédemment, il existe le concept de bon suffixe dans l'algorithme bm, et il existe le concept de bon préfixe dans kmp. Qu'est-ce qu'un bon préfixe ? Regardons d'abord l'exemple suivant.

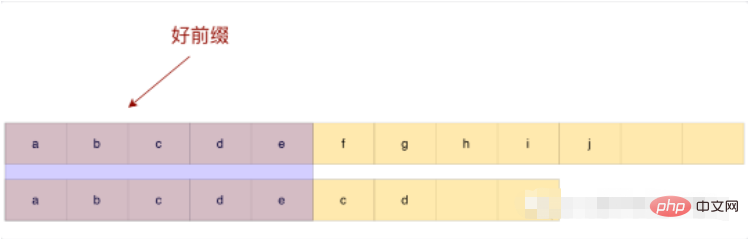
Observez l'exemple ci-dessus, l'abcde correspondant est appelé un bon préfixe, a ne correspond pas au bcde suivant, il n'est donc pas nécessaire de comparer à nouveau , Glissez simplement directement après e.

Et s'il y a des caractères qui se correspondent dans le bon préfixe ?

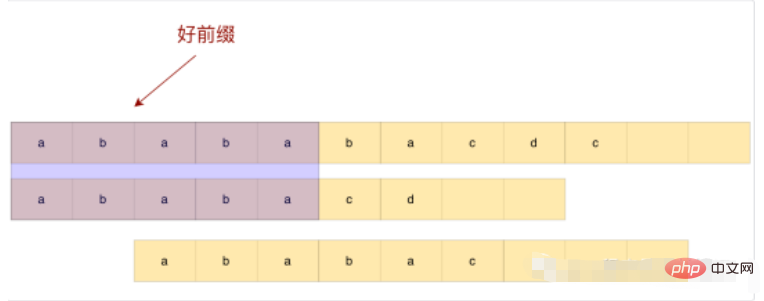
Observez l'exemple ci-dessus Si nous glissons directement après le préfixe, nous glisserons trop et manquerons la sous-chaîne correspondante. Alors, comment pouvons-nous effectuer un glissement raisonnable basé sur de bons préfixes ?

En fait, il s'agit de vérifier si le préfixe et le suffixe du bon préfixe actuel correspondent, de trouver la longueur correspondante la plus longue et de glisser directement. Afin de trouver la longueur correspondante la plus longue plus d'une fois, nous pouvons d'abord initialiser un tableau et enregistrer la longueur correspondante la plus longue sous le bon préfixe actuel. À ce moment-là, notre prochain tableau sortira.

Nous définissons un tableau suivant, qui représente la longueur de sous-chaîne correspondante la plus longue du préfixe et du suffixe du bon préfixe sous le bon préfixe actuel. Cette longueur correspondante la plus longue signifie que cette sous-chaîne a déjà été mise en correspondance. pas besoin de faire une nouvelle correspondance, commencez la correspondance directement à partir du caractère suivant de la sous-chaîne.

Devons-nous faire correspondre chaque personnage à chaque fois que nous comptons next[i] ? Pouvons-nous le déduire en fonction de next[i - 1] pour que Réduisez les comparaisons inutiles.

Avec cette idée, jetons un œil aux étapes suivantes :

Assume next[i - 1] = k - 1;

If modelStr [k] = modelStr[i] then next[i]=k

If modelStr[k] != modelStr[i], pouvons-nous Déterminer directement next[i] = next[i - 1] ?

Grâce à l'exemple ci-dessus, on voit clairement que next[i]!=next[i-1], puis quand modelStr[ k]! =modelStr[i], on connaît déjà next[0], next[1]…next[i-1], comment déduire next[i] ?

En supposant que modelStr[x…i] est la sous-chaîne de suffixe la plus longue à laquelle le préfixe et le suffixe peuvent correspondre, alors la sous-chaîne de préfixe correspondante la plus longue est modelStr[0…i-x]

# 🎜🎜#

Lorsque nous trouvons la chaîne correspondante la plus longue, sa deuxième chaîne correspondante la plus longue précédente (à l'exclusion du i actuel), c'est-à-dire modelStr[x…i-1] est avant Cela aurait dû être résolu, nous n'avons donc besoin que de trouver cette chaîne correspondante qui a été résolue. Supposons que la sous-chaîne de préfixe est modelStr[0…i-x-1], la sous-chaîne de suffixe est modelStr[x…i-1] et modelStr[i-x] = = modelStr[i], cette sous-chaîne de préfixe et de suffixe est la sous-chaîne de préfixe secondaire, et le caractère actuel est la sous-chaîne de préfixe et de suffixe correspondante la plus longue.

Implémentation du code

Tout d'abord, le tableau suivant le plus important de l'algorithme kmp Ce tableau marque le nombre de préfixes et de suffixes correspondant aux caractères de sous-chaîne jusqu'à l'indice actuel. , kmp Dans l'algorithme, si un certain préfixe est un bon préfixe, c'est-à-dire qu'il correspond au préfixe de chaîne de modèle, nous pouvons utiliser certaines techniques pour faire glisser plus d'un caractère vers l'avant. Voir l'explication précédente pour plus de détails. Nous ne savons pas à l'avance quels sont les bons préfixes, et le processus de correspondance est effectué plusieurs fois, nous appelons donc une méthode d'initialisation au début pour initialiser le tableau suivant.

1. Si le caractère suivant de la sous-chaîne de préfixe la plus longue du caractère précédent == le caractère actuel, la sous-chaîne de préfixe la plus longue du caractère précédent peut être directement ajoutée au caractère actuel

# 🎜🎜#2. S'il n'est pas égal, vous devez rechercher le caractère suivant de la sous-chaîne de préfixe la plus longue existante qui est égale à la sous-chaîne actuelle, puis définir la sous-chaîne de suffixe de préfixe la plus longue de la sous-chaîne de caractères actuelle

int[] next ;
    /**
     * 初始化next数组
     * @param modelStr
     */
    public void init(char[] modelStr) {
        //首先计算next数组
        //遍历modelStr，遍历到的字符与之前字符组成一个串
        next = new int[modelStr.length];
        int start = 0;
        while (start < modelStr.length) {
            next[start] = this.recursion(start, modelStr);
            ++ start;
        }
    }

    /**
     *
     * @param i 当前遍历到的字符
     * @return
     */
    private int recursion(int i, char[] modelStr) {
        //next记录的是个数，不是下标
        if (0 == i) {
            return 0;
        }
        int last = next[i -1];
        //没有匹配的,直接判断第一个是否匹配
        if (0 == last) {
            if (modelStr[last] == modelStr[i]) {
                return 1;
            }
            return 0;
        }
        //如果last不为0，有值，可以作为最长匹配的前缀
        if (modelStr[last] == modelStr[i]) {
            return next[i - 1] + 1;
        }
        //当next[i-1]对应的子串的下一个值与modelStr不匹配时，需要找到当前要找的最长匹配子串的次长子串
        //依据就是次长子串对应的子串的下一个字符==modelStr[i];
        int tempIndex = i;
        while (tempIndex > 0) {
            last = next[tempIndex - 1];
            //找到第一个下一个字符是当前字符的匹配子串
            if (modelStr[last] == modelStr[i]) {
                return last + 1;
            }
            -- tempIndex;
        }
        return 0;
    }

# 🎜🎜 #Ensuite, commencez à utiliser le tableau suivant pour la correspondance, commencez la correspondance à partir du premier caractère et recherchez le premier caractère sans correspondance. À ce moment, tous les précédents correspondent. Ensuite, déterminez s'il s'agit d'une correspondance complète et revenez directement. , non, à en juger si le premier ne correspond pas, il correspond directement au dos. S'il existe un bon préfixe, le tableau suivant est utilisé à ce moment-là. Grâce au tableau suivant, nous savons où la correspondance actuelle peut commencer, et il n'est pas nécessaire de faire correspondre les précédents.

public int kmp(char[] mainStr, char[] modelStr) {
        //开始进行匹配
        int i = 0, j = 0;
        while (i + modelStr.length <= mainStr.length) {
            while (j < modelStr.length) {
                //找到第一个不匹配的位置
                if (modelStr[j] != mainStr[i]) {
                    break;
                }
                ++ i;
                ++ j;
            }
            if (j == modelStr.length) {
                //证明完全匹配
                return i - j;
            }
            //走到这里找到的是第一个不匹配的位置
            if (j == 0) {
                ++ i;
                continue;
            }
            //从好前缀后一个匹配
            j = next[j - 1];
        }
        return -1;
    }

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!