 développement back-end
développement back-end
 Tutoriel Python
Tutoriel Python
 Fonctions de perte couramment utilisées et exemples d'implémentation Python
Fonctions de perte couramment utilisées et exemples d'implémentation Python
Fonctions de perte couramment utilisées et exemples d'implémentation Python
Qu'est-ce que la fonction de perte ?
La fonction de perte est un algorithme qui mesure dans quelle mesure le modèle s'adapte aux données. Une fonction de perte est un moyen de mesurer la différence entre les mesures réelles et les valeurs prédites. Plus la valeur de la fonction de perte est élevée, plus la prédiction est incorrecte, et plus la valeur de la fonction de perte est faible, plus la prédiction est proche de la valeur réelle. La fonction de perte est calculée pour chaque observation individuelle (point de données). La fonction qui fait la moyenne des valeurs de toutes les fonctions de perte est appelée fonction de coût. Une compréhension plus simple est que la fonction de perte concerne un seul échantillon, tandis que la fonction de coût concerne tous les échantillons.
Fonctions et métriques de perte
Certaines fonctions de perte peuvent également être utilisées comme métriques d'évaluation. Mais les fonctions et mesures de perte ont des objectifs différents. Alors que les métriques sont utilisées pour évaluer le modèle final et comparer les performances de différents modèles, la fonction de perte est utilisée pendant la phase de création du modèle comme optimiseur pour le modèle en cours de création. La fonction de perte guide le modèle sur la manière de minimiser l'erreur.
C'est-à-dire que la fonction de perte sait comment le modèle est entraîné et l'indice de mesure explique les performances du modèle
Pourquoi utiliser la fonction de perte
Puisque la fonction de perte mesure la différence entre la valeur prédite et ? la valeur réelle, ils peuvent donc être utilisés pour guider l'amélioration du modèle lors de l'entraînement du modèle (généralement une descente de gradient). Dans le processus de construction du modèle, si le poids de la fonctionnalité change et obtient des prévisions meilleures ou pires, vous devez utiliser la fonction de perte pour juger si le poids de la fonctionnalité dans le modèle doit être modifié et la direction du changement. .
Nous pouvons utiliser une variété de fonctions de perte dans l'apprentissage automatique, en fonction du type de problème que nous essayons de résoudre, de la qualité et de la distribution des données, ainsi que de l'algorithme que nous utilisons. La figure suivante montre les 10 fonctions de perte courantes que nous avons compilées. . :
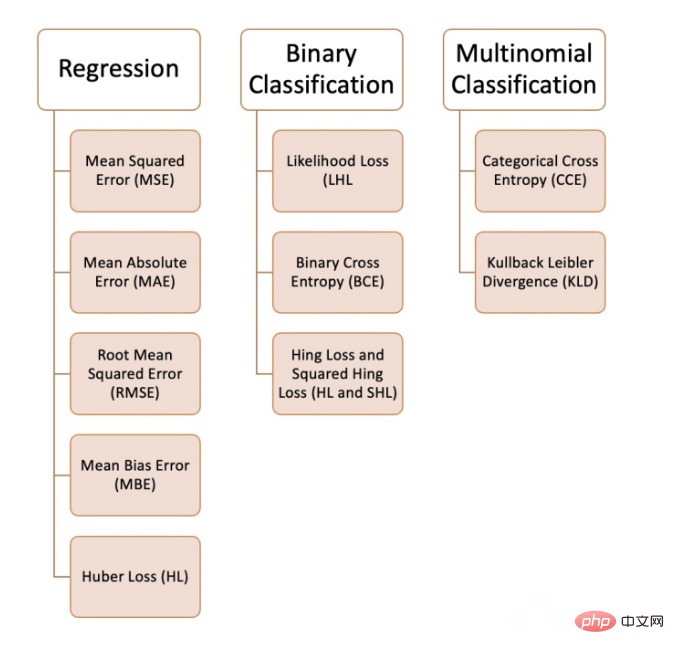
Problème de régression
1. Erreur quadratique moyenne (MSE)
L'erreur quadratique moyenne fait référence à la différence quadratique entre toutes les valeurs prédites et la valeur vraie, et les fait en moyenne. Souvent utilisé dans les problèmes de régression.
def MSE (y, y_predicted): sq_error = (y_predicted - y) ** 2 sum_sq_error = np.sum(sq_error) mse = sum_sq_error/y.size return mse
2. L'erreur absolue moyenne (MAE)
est calculée comme la moyenne des différences absolues entre la valeur prédite et la valeur vraie. Il s'agit d'une meilleure mesure que l'erreur quadratique moyenne lorsque les données comportent des valeurs aberrantes.
def MAE (y, y_predicted): error = y_predicted - y absolute_error = np.absolute(error) total_absolute_error = np.sum(absolute_error) mae = total_absolute_error/y.size return mae
3. Erreur quadratique moyenne (RMSE)
Cette fonction de perte est la racine carrée de l'erreur quadratique moyenne. C'est une approche idéale si nous ne voulons pas punir des erreurs plus importantes.
def RMSE (y, y_predicted): sq_error = (y_predicted - y) ** 2 total_sq_error = np.sum(sq_error) mse = total_sq_error/y.size rmse = math.sqrt(mse) return rmse
4. L'erreur de biais moyenne (MBE)
est similaire à l'erreur absolue moyenne mais ne recherche pas la valeur absolue. L’inconvénient de cette fonction de perte est que les erreurs négatives et positives peuvent s’annuler, il est donc préférable de l’appliquer lorsque le chercheur sait que l’erreur ne va que dans un seul sens.
def MBE (y, y_predicted): error = y_predicted -y total_error = np.sum(error) mbe = total_error/y.size return mbe
5. Perte de Huber
La fonction de perte de Huber combine les avantages de l'erreur absolue moyenne (MAE) et de l'erreur quadratique moyenne (MSE). En effet, la perte de Hubber est une fonction à deux branches. Une branche est appliquée aux MAE qui correspondent aux valeurs attendues, et l'autre branche est appliquée aux valeurs aberrantes. La fonction générale de Hubber Loss est :
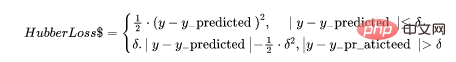
Ici
def hubber_loss (y, y_predicted, delta) delta = 1.35 * MAE y_size = y.size total_error = 0 for i in range (y_size): erro = np.absolute(y_predicted[i] - y[i]) if error < delta: hubber_error = (error * error) / 2 else: hubber_error = (delta * error) / (0.5 * (delta * delta)) total_error += hubber_error total_hubber_error = total_error/y.size return total_hubber_error
Classification binaire
6. Perte de vraisemblance maximale (Perte de vraisemblance/LHL)
Cette fonction de perte est principalement utilisée pour les problèmes de classification binaire. La probabilité de chaque valeur prédite est multipliée pour obtenir une valeur de perte, et la fonction de coût associée est la moyenne de toutes les valeurs observées. Prenons l'exemple suivant de classification binaire où la classe est [0] ou [1]. Si la probabilité de sortie est égale ou supérieure à 0,5, la classe prédite est [1], sinon elle est [0]. Un exemple de probabilité de sortie est le suivant :
[0.3 , 0.7 , 0.8 , 0.5 , 0.6 , 0.4]
La classe prédite correspondante est :
[0 , 1 , 1 , 1 , 1 , 0]
Et la classe réelle est :
[0 , 1 , 1 , 0 , 1 , 0]
Maintenant, la classe réelle et la probabilité de sortie seront utilisées pour calculer la perte. Si la vraie classe est [1], nous utilisons la probabilité de sortie. Si la vraie classe est [0], nous utilisons la probabilité 1 :
((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65
Le code Python est le suivant :
def LHL (y, y_predicted): likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted)) total_likelihood_loss = np.sum(likelihood_loss) lhl = - total_likelihood_loss / y.size return lhl
7. BCE)
Cette fonction est une correction de la perte de log-vraisemblance. L’empilement de séquences de nombres peut pénaliser des prédictions très sûres mais incorrectes. La formule générale de la fonction binaire de perte d'entropie croisée est :
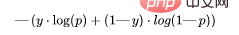
Continuons à utiliser les valeurs de l'exemple ci-dessus :
- Probabilité de sortie = [0.3, 0.7, 0.8, 0.5, 0.6, 0.4 ]
- Classe réelle = [0, 1, 1, 0, 1, 0]
- (0 . log (0,3) + (1–0) . log (1–0,3)) = 0,155
- (1 . log(0,7 ) + (1–1) . log (0,3)) = 0,155
- (1 . log(0,8) + (1–1) . log (0,2)) = 0,097
- (0 . log (0,5 ) + (1 –0) . log (1–0,5)) = 0,301
- (1 . log(0,6) + (1–1) . log (0,4)) = 0,222
- (0 . log (0,4) + (1–0 ) . log (1–0.4)) = 0,222
Alors le résultat de la fonction de coût est :
(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192
Le code Python est le suivant :
def BCE (y, y_predicted): ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted)) total_ce = np.sum(ce_loss) bce = - total_ce/y.size return bce
8, perte de charnière et perte de charnière carrée (HL et SHL)
La perte de charnière est traduite en perte de charnière ou perte de charnière, l'anglais prévaudra ici.
Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。所以一般损失函数是:
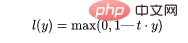
这里的t是真实结果用[1]或[-1]表示。
使用Hinge Loss的类应该是[1]或-1。为了在Hinge loss函数中不被惩罚,一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差,我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。
如果你对SVM比较熟悉,应该还记得在SVM中,超平面的边缘(margin)越高,则某一预测就越有信心。如果这块不熟悉,则看看这个可视化的例子:
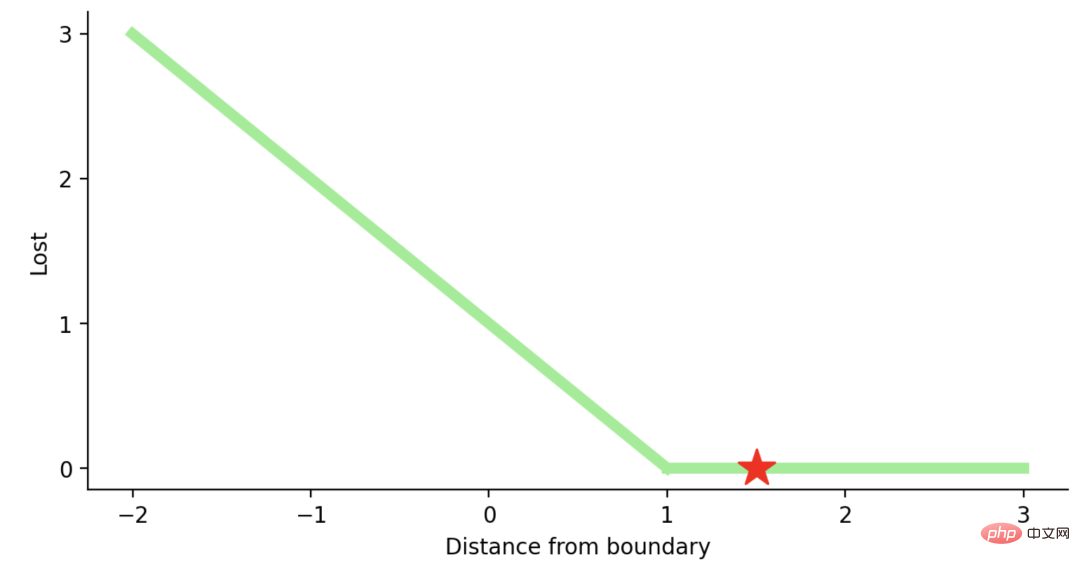
如果一个预测的结果是1.5,并且真正的类是[1],损失将是0(零),因为模型是高度自信的。
loss= Max (0,1 - 1* 1.5) = Max (0, -0.5) = 0
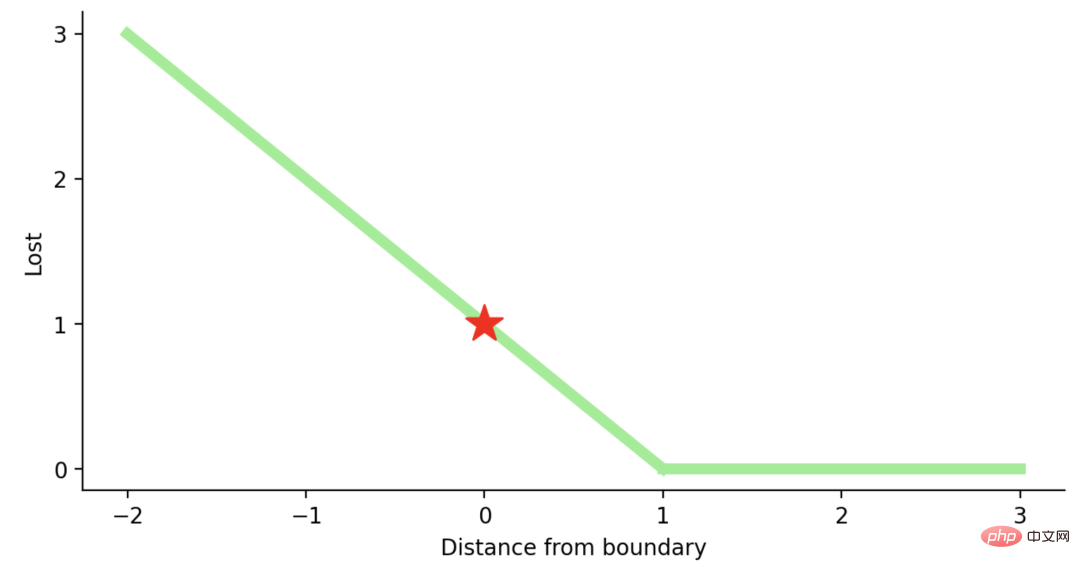
如果一个观测结果为0(0),则表示该观测处于边界(超平面),真实的类为[-1]。损失为1,模型既不正确也不错误,可信度很低。
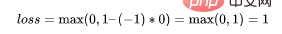
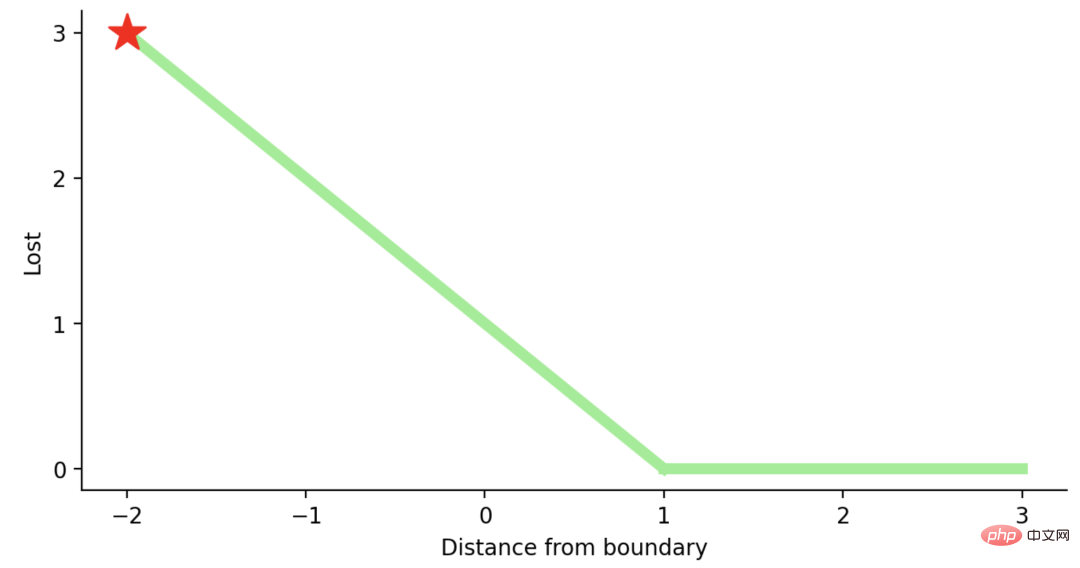
如果一次观测结果为2,但分类错误(乘以[-1]),则距离为-2。损失是3(非常高),因为我们的模型对错误的决策非常有信心(这个是绝不能容忍的)。
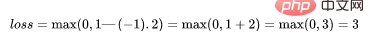
python代码如下:
#Hinge Loss def Hinge (y, y_predicted): hinge_loss = np.sum(max(0 , 1 - (y_predicted * y))) return hinge_loss #Squared Hinge Loss def SqHinge (y, y_predicted): sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2 total_sq_hinge_loss = np.sum(sq_hinge_loss) return total_sq_hinge_loss
多分类
9、交叉熵(CE)
在多分类中,我们使用与二元交叉熵类似的公式,但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失,一般公式为:
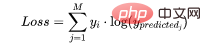
如果我们有三个类,其中单个[y, y_predicted]对的输出是:

这里实际的类3(也就是值=1的部分),我们的模型对真正的类是3的信任度是0.7。计算这损失如下:
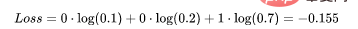
为了得到代价函数的值,我们需要计算所有单个配对的损失,然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出:
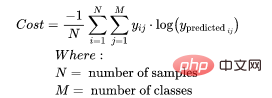
使用上面的例子,如果我们的第二对:

那么成本函数计算如下:
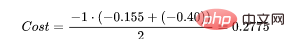
使用Python的代码示例可以更容易理解;
def CCE (y, y_predicted): cce_class = y * (np.log(y_predicted)) sum_totalpair_cce = np.sum(cce_class) cce = - sum_totalpair_cce / y.size return cce
10、Kullback-Leibler 散度 (KLD)
又被简化称为KL散度,它类似于分类交叉熵,但考虑了观测值发生的概率。如果我们的类不平衡,它特别有用。
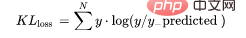
def KL (y, y_predicted): kl = y * (np.log(y / y_predicted)) total_kl = np.sum(kl) return total_kl
以上就是常见的10个损失函数,希望对你有所帮助。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL a une version communautaire gratuite et une version d'entreprise payante. La version communautaire peut être utilisée et modifiée gratuitement, mais le support est limité et convient aux applications avec des exigences de stabilité faibles et des capacités techniques solides. L'Enterprise Edition fournit une prise en charge commerciale complète pour les applications qui nécessitent une base de données stable, fiable et haute performance et disposées à payer pour le soutien. Les facteurs pris en compte lors du choix d'une version comprennent la criticité des applications, la budgétisation et les compétences techniques. Il n'y a pas d'option parfaite, seulement l'option la plus appropriée, et vous devez choisir soigneusement en fonction de la situation spécifique.
 HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: Une base de données Python évolutive de haut niveau légère HaDIDB (HaDIDB) est une base de données légère écrite en Python, avec un niveau élevé d'évolutivité. Installez HaDIDB à l'aide de l'installation PIP: PiPinStallHaDIDB User Management Créer un utilisateur: CreateUser () pour créer un nouvel utilisateur. La méthode Authentication () authentifie l'identité de l'utilisateur. FromHadidb.OperationMportUserUser_OBJ = User ("Admin", "Admin") User_OBJ.
 Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Il est impossible de visualiser le mot de passe MongoDB directement via NAVICAT car il est stocké sous forme de valeurs de hachage. Comment récupérer les mots de passe perdus: 1. Réinitialiser les mots de passe; 2. Vérifiez les fichiers de configuration (peut contenir des valeurs de hachage); 3. Vérifiez les codes (May Code Hardcode).
 MySQL a-t-il besoin d'Internet
Apr 08, 2025 pm 02:18 PM
MySQL a-t-il besoin d'Internet
Apr 08, 2025 pm 02:18 PM
MySQL peut s'exécuter sans connexions réseau pour le stockage et la gestion des données de base. Cependant, la connexion réseau est requise pour l'interaction avec d'autres systèmes, l'accès à distance ou l'utilisation de fonctionnalités avancées telles que la réplication et le clustering. De plus, les mesures de sécurité (telles que les pare-feu), l'optimisation des performances (choisissez la bonne connexion réseau) et la sauvegarde des données sont essentielles pour se connecter à Internet.
 Comment résoudre MySQL ne peut pas se connecter à l'hôte local
Apr 08, 2025 pm 02:24 PM
Comment résoudre MySQL ne peut pas se connecter à l'hôte local
Apr 08, 2025 pm 02:24 PM
La connexion MySQL peut être due aux raisons suivantes: le service MySQL n'est pas démarré, le pare-feu intercepte la connexion, le numéro de port est incorrect, le nom d'utilisateur ou le mot de passe est incorrect, l'adresse d'écoute dans my.cnf est mal configurée, etc. 2. Ajustez les paramètres du pare-feu pour permettre à MySQL d'écouter le port 3306; 3. Confirmez que le numéro de port est cohérent avec le numéro de port réel; 4. Vérifiez si le nom d'utilisateur et le mot de passe sont corrects; 5. Assurez-vous que les paramètres d'adresse de liaison dans My.cnf sont corrects.
 MySQL Workbench peut-il se connecter à MariaDB
Apr 08, 2025 pm 02:33 PM
MySQL Workbench peut-il se connecter à MariaDB
Apr 08, 2025 pm 02:33 PM
MySQL Workbench peut se connecter à MARIADB, à condition que la configuration soit correcte. Sélectionnez d'abord "MariADB" comme type de connecteur. Dans la configuration de la connexion, définissez correctement l'hôte, le port, l'utilisateur, le mot de passe et la base de données. Lorsque vous testez la connexion, vérifiez que le service MARIADB est démarré, si le nom d'utilisateur et le mot de passe sont corrects, si le numéro de port est correct, si le pare-feu autorise les connexions et si la base de données existe. Dans une utilisation avancée, utilisez la technologie de mise en commun des connexions pour optimiser les performances. Les erreurs courantes incluent des autorisations insuffisantes, des problèmes de connexion réseau, etc. Lors des erreurs de débogage, analysez soigneusement les informations d'erreur et utilisez des outils de débogage. L'optimisation de la configuration du réseau peut améliorer les performances
 Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Guide d'optimisation des performances de la base de données MySQL dans les applications à forte intensité de ressources, la base de données MySQL joue un rôle crucial et est responsable de la gestion des transactions massives. Cependant, à mesure que l'échelle de l'application se développe, les goulots d'étranglement des performances de la base de données deviennent souvent une contrainte. Cet article explorera une série de stratégies efficaces d'optimisation des performances MySQL pour garantir que votre application reste efficace et réactive dans des charges élevées. Nous combinerons des cas réels pour expliquer les technologies clés approfondies telles que l'indexation, l'optimisation des requêtes, la conception de la base de données et la mise en cache. 1. La conception de l'architecture de la base de données et l'architecture optimisée de la base de données sont la pierre angulaire de l'optimisation des performances MySQL. Voici quelques principes de base: sélectionner le bon type de données et sélectionner le plus petit type de données qui répond aux besoins peut non seulement économiser un espace de stockage, mais également améliorer la vitesse de traitement des données.
 Comment utiliser Aws Glue Crawler avec Amazon Athena
Apr 09, 2025 pm 03:09 PM
Comment utiliser Aws Glue Crawler avec Amazon Athena
Apr 09, 2025 pm 03:09 PM
En tant que professionnel des données, vous devez traiter de grandes quantités de données provenant de diverses sources. Cela peut poser des défis à la gestion et à l'analyse des données. Heureusement, deux services AWS peuvent aider: AWS Glue et Amazon Athena.





