Exemple d'analyse de union-find en Java

1. Présentation

Union-find : une structure de données de type arborescent utilisée pour résoudre certains problèmes de fusion et d'interrogation d'ensembles disjoints. Par exemple : il y a n villages, demandez s'il existe une route de liaison entre les deux villages, reliant les deux villages

Deux noyaux :

Find (Find) : Trouver l'ensemble où se trouve l'élément

Union (Union) : Combiner les deux Les ensembles d'éléments sont fusionnés en un seul ensemble

2. Implémentation de

Recherche d'union Il existe deux idées d'implémentation courantes

Recherche rapide

• Complexité temporelle de la recherche : O(1)

• Temps complexité de l'Union : O(n)

Union rapide

• Complexité temporelle de la recherche : O(logn) peut être optimisé en O(a (n))a(n)

• Time complexité de l'Union : O(logn) peut être optimisé en O(a(n))a(n)

en utilisant Le tableau implémente une structure arborescente, l'indice du tableau est l'élément et la valeur stockée dans le tableau est la valeur du nœud parent

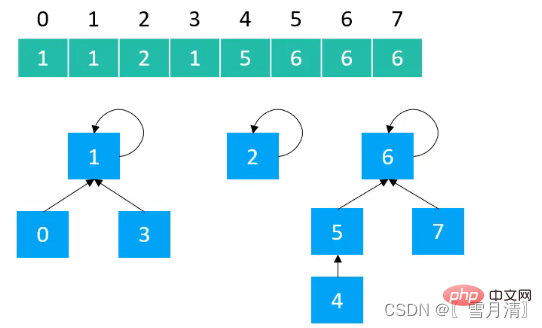
Créer la classe abstraite Union Find

public abstract class UnionFind {
 
	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){
		
		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}
	
   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}
 
    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);
 
	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);
	
		
	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Implémentation de la recherche rapide

Recherche d'union implémentée avec Quick Find, tree La hauteur maximale de Lorsque l'arbre est déséquilibré

Il existe deux idées d'optimisation : l'optimisation du classement et l'optimisation de la taille

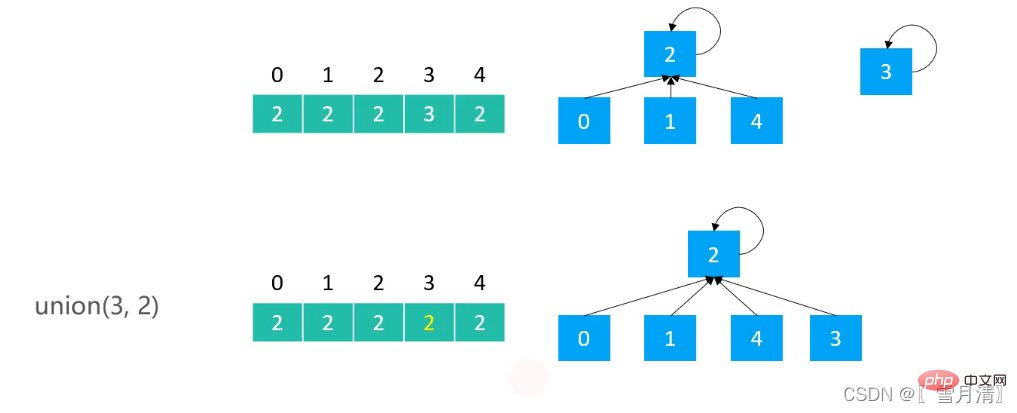
3.1 Optimisation basée sur la taille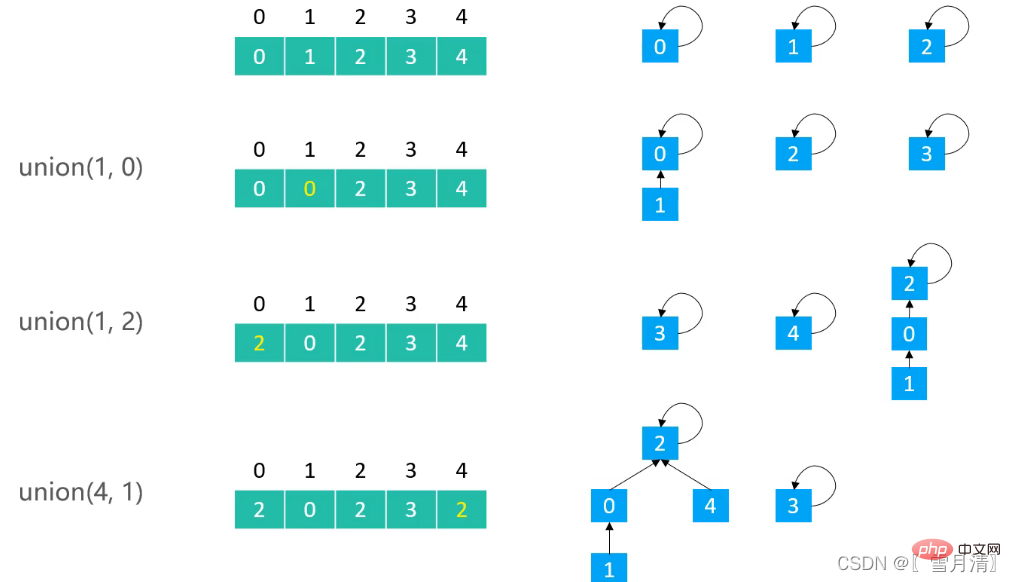

Idée de base : un arbre avec peu d'éléments est greffé à un arbre avec de nombreux éléments

public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
		
	}
 
  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}
 
 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;
  
    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}
	
  }
}

Optimisation basée sur la taille Cela peut également provoquer l'arbre être déséquilibré

3.2 Optimisation basée sur le classement

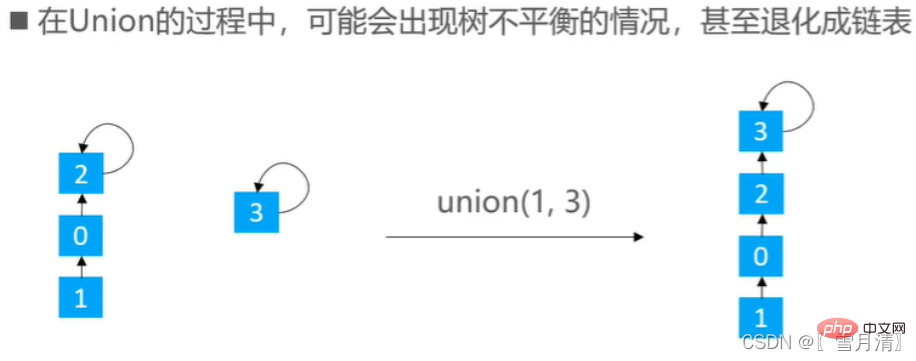Idée de base : greffer un arbre court sur un grand arbre

public class UnionFind_QU extends UnionFind {
 
	public UnionFind_QU(int capacity) {
		super(capacity);
		
	}
 
	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);
   
  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

Basé sur l'optimisation du classement, à mesure que le nombre d'unions augmente, la hauteur de l'arbre deviendra de plus en plus élevée. Causes l'opération de recherche pour ralentir

Il y a trois idées pour continuer à optimiser : la compression du chemin, la division du chemin et la réduction de moitié du chemin

3.2.1 Compression du chemin (compression du chemin)

Faites en sorte que tous les nœuds du chemin pointent vers le nœud racine lorsque découverte, réduisant ainsi la hauteur de l'arbre

public class UniondFind_QU_S extends UnionFind{
 
   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;
 
	public UniondFind_QU_S(int capacity) {
		super(capacity);
 
		sizes = new int[capacity];
 
   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}
		
	}
 
	@Override
	public int find(int v) {
 
		rangeCheck(v);
 
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
 
		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];
		
 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

Bien que cela puisse réduire la hauteur de l'arbre, le coût de mise en œuvre est légèrement plus élevé

3.2.2 Division du chemin

Faites en sorte que chaque nœud du chemin pointe vers son grand-parent node

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;
 
	public UnionFind_QU_R(int capacity) {
		super(capacity);
 
		ranks = new int[capacity];
 
		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}
 
	}
    
	public void union(int v1, int v2) {
 
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
    
    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
			
  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
 
		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

3.2.3 Réduire de moitié le chemin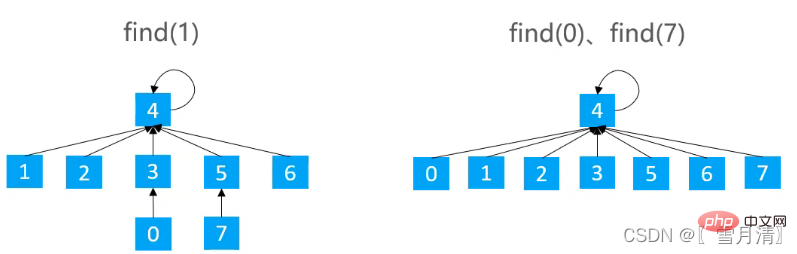

Faire en sorte que tous les autres nœuds du chemin pointent vers son nœud grand-parent

/**
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
 
		if(parents[v] != v) {
 
        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

Utiliser Quick Union + optimisation basée sur le classement + division du chemin ou réduction de moitié du chemin

Il peut être garanti que la complexité temporelle amortie de chaque opération est O(a(n)), a(n)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!