
En Java, de nombreuses classes doivent être traitées, comme la classe Integer, mais la classe Integer a également une limite supérieure. Sa valeur maximale est 2^31-1.
Si nous voulons représenter un nombre plus grand à ce moment, il ne peut pas être représenté par Integer, donc Java fournit la classe BigInteger.
Les nombres pris en charge par la classe BigInteger peuvent être considérés comme infinis, et elle prend en charge les entiers de précision arbitraire, ce qui signifie qu'elle peut représenter avec précision n'importe quelle valeur sans perte.
Je voudrais également souligner ici que le type de numéro entrant étant un type de caractère, vous ne pouvez pas utiliser + - * lorsque vous effectuez des opérations /
correspond aux méthodes d'utilisation :
add(), soustract(. ), multiplier(), diviser()
et quelques méthodes courantes :
méthode equals. À titre de comparaison
Démonstration du code :
import java.math.BigInteger;
public class Demo01 {
public static void main(String[] args) {
BigInteger bigInteger1 = new BigInteger("2222222222222222222222222222222");
BigInteger bigInteger2 = new BigInteger("1111111111111111111111111111111");
System.out.println("bigInteger1大数为:" + bigInteger1);
System.out.println("bigInteger2大数为:" + bigInteger2);
System.out.println("两个大数相加:" + bigInteger1.add(bigInteger2));//加
System.out.println("两个大数相减:" + bigInteger1.subtract(bigInteger2));//减
System.out.println("两个大数相乘:" + bigInteger1.multiply(bigInteger2));//乘
System.out.println("两个大数相除:" + bigInteger1.divide(bigInteger2));//除
System.out.println("两个大数相比:" + bigInteger1.equals(bigInteger2));//equals进行比较
}
}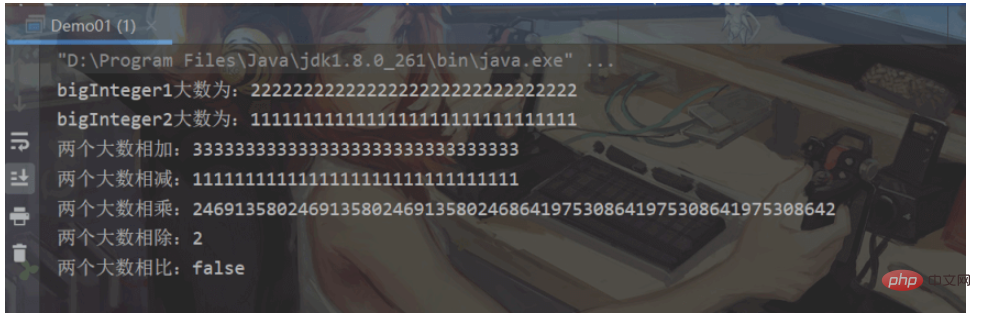
Lors de la division, s'il y a des décimales, les décimales sont interceptées ici.
Bien sûr, il existe non seulement des types entiers, mais aussi des types à virgule flottante.
Bien sûr, la précision de la virgule flottante peut être aussi grande que possible.
import java.math.BigDecimal;
public class Demo02 {
public static void main(String[] args) {
BigDecimal bigDecimal1 = new BigDecimal("12232423432432.53241234324");
BigDecimal bigDecimal2 = new BigDecimal("2.0");
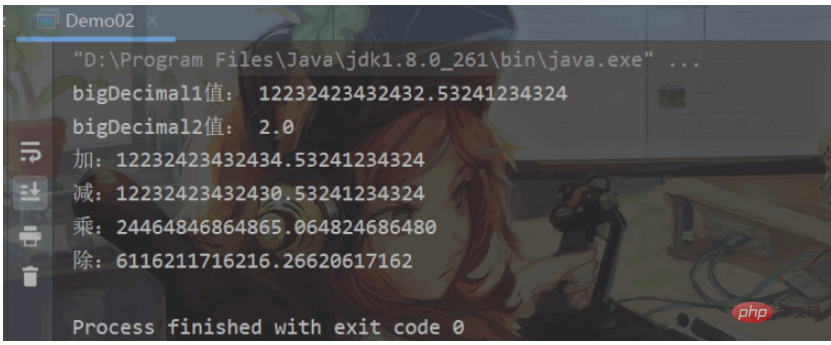
System.out.println("bigDecimal1值: " + bigDecimal1);
System.out.println("bigDecimal2值: " + bigDecimal2);
System.out.println("加:" + bigDecimal1.add(bigDecimal2));
System.out.println("减:" + bigDecimal1.subtract(bigDecimal2));
System.out.println("乘:" + bigDecimal1.multiply(bigDecimal2));
System.out.println("除:" + bigDecimal1.divide(bigDecimal2));
}
}
Dans la méthode BigDecimal, cela peut également mieux résoudre le problème de précision dans le langage Java (comme le problème que le résultat de 0,1x3 == 0,3 est faux)
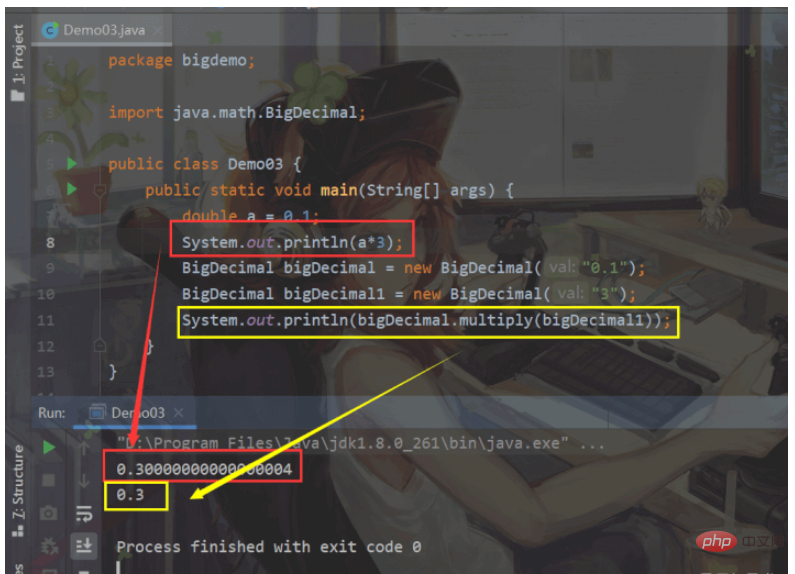
Mais il y a un point auquel vous devez faire attention lorsque vous utilisez BigDecimal (lorsqu'il rencontre quelque chose qui ne peut pas être divisé, il choisira de signaler une erreur.)
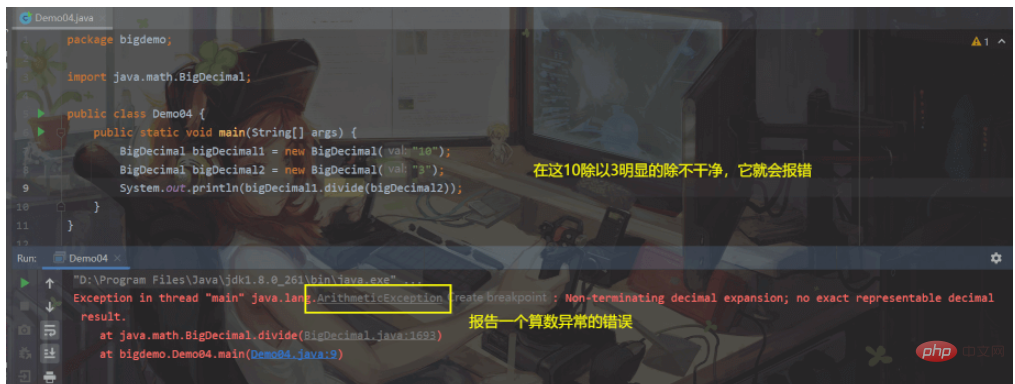
Donc, lors de la division , donnez-lui juste un peu d'interception.
Regardons d'abord une méthode :
division BigDecimal publique (diviseur BigDecimal, échelle int, mode d'arrondi int)
diviseur - diviseur.
scale - Combien de décimales conserver
roundingMode - Choisissez le mode d'arrondi
Nous pouvons donc l'écrire comme ceci :
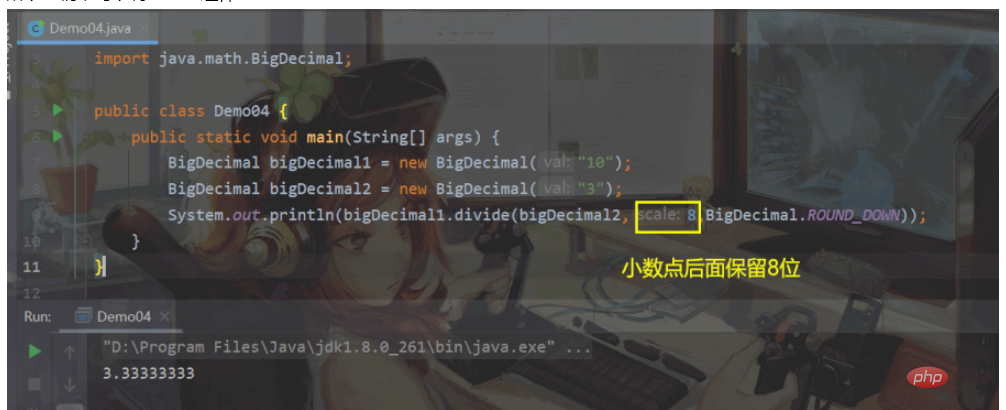
Sélection du mode d'arrondi :
| Mode | signifiant |
|---|---|
| ROUND_CEILING | Récupérer vers l'infini positif |
| ROUND_DOWN | Récupérer vers 0 |
| ROUND_FLOOR | Récupérer vers l'infini négatif |
| ROUND_HALF _ DOWN | Arrondissez à l'inférieur lorsque vous rencontrez .5 |
| ROUND_HALF_UP | Arrondissez lorsque vous rencontrez 0,5 et prenez le nombre vers le haut |
| ROUND_HALF_EVEN | Arrondissez lorsque vous rencontrez 5 et regardez le nombre précédent s'il est supérieur à 5, il augmentera, s'il est inférieur à 5, il descendra. S'il est égal à 5, il attendra. |
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!