Aujourd'hui, j'aimerais vous présenter un article sur la prédiction de séries chronologiques multivariées publié sur arixv en 2023.1. Le point de départ est assez intéressant : comment améliorer l'équité des séries chronologiques multivariées. Les méthodes de modélisation utilisées dans cet article sont toutes des opérations conventionnelles qui ont été utilisées dans la prédiction spatio-temporelle, l'adaptation de domaine, etc., mais l'enjeu de l'équité multivariable est relativement nouveau.
Le problème de l'équité est un concept macro dans le domaine de l'apprentissage automatique. Une compréhension de l'équité dans l'apprentissage automatique est la cohérence de l'effet d'ajustement d'un modèle sur différents échantillons. Si un modèle fonctionne bien sur certains échantillons et mal sur d’autres, alors le modèle est moins juste. Par exemple, un scénario courant est que dans un système de recommandation, l'effet de prédiction du modèle sur les échantillons de tête est meilleur que celui des échantillons de queue, ce qui reflète l'injustice de l'effet de prédiction du modèle sur différents échantillons.
De retour au problème de prédiction de séries chronologiques multivariées, l'équité fait référence à la question de savoir si le modèle a un meilleur effet de prédiction sur chaque variable. Si l’effet de prédiction du modèle sur différentes variables est très différent, alors ce modèle de prévision de séries chronologiques multivariées est injuste. Par exemple, dans l'exemple de la figure ci-dessous, la première ligne du tableau représente la variance du MAE des effets de prédiction de différents modèles sur chaque variable. On peut voir qu'il existe un certain degré d'injustice dans différents modèles. La séquence dans l'image ci-dessous est un exemple. Certaines séquences sont meilleures pour prédire, tandis que d'autres sont moins bonnes.
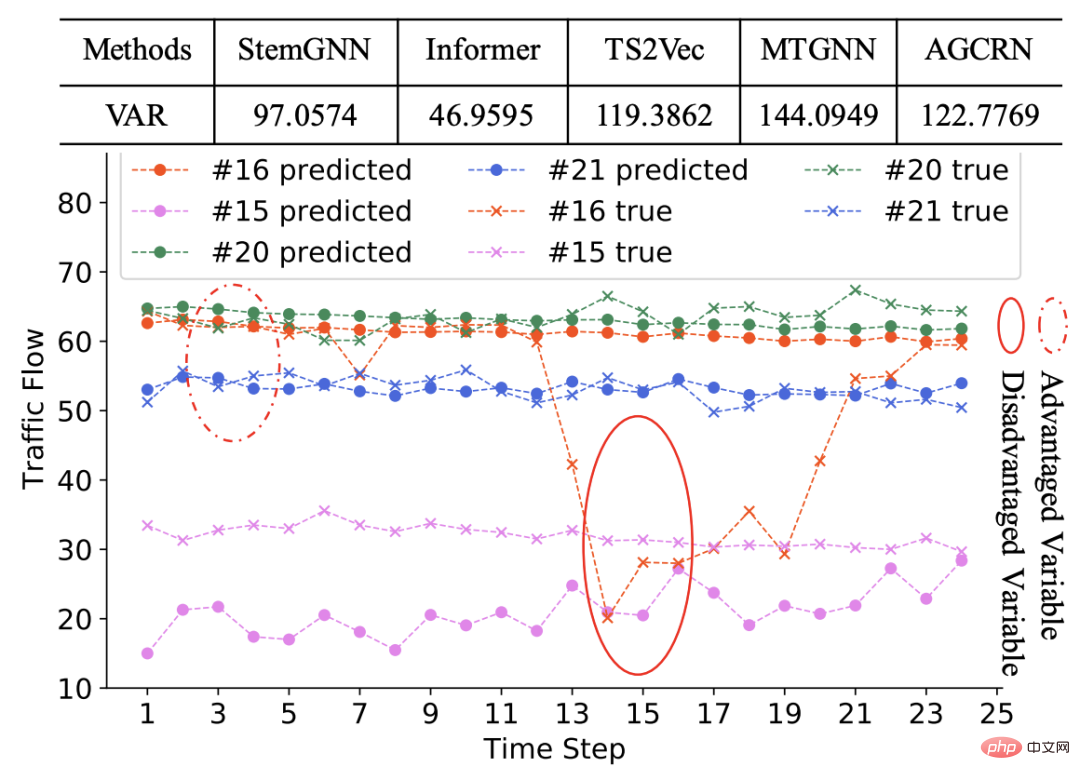
Pourquoi l'injustice se produit-elle ? Qu'il s'agisse de séries chronologiques multivariées ou d'autres domaines d'apprentissage automatique, l'une des principales raisons des grandes différences dans les effets de prédiction des différents échantillons est que différents échantillons ont des caractéristiques différentes et que le modèle peut être dominé par les caractéristiques de certains échantillons pendant le processus de formation. , ce qui entraîne que le modèle prédit bien sur les échantillons qui dominent l'entraînement, mais mal sur les échantillons non dominés.
Dans les séries chronologiques multivariées, différentes variables peuvent avoir des modèles de séquence très différents. Par exemple, dans l’exemple ci-dessus, la plupart des séquences sont stationnaires, ce qui domine le processus de formation du modèle. Cependant, un petit nombre de séquences présentent une volatilité différente des autres séquences, ce qui entraîne un mauvais effet de prédiction du modèle sur ces séquences.
Comment résoudre l'injustice dans les séries temporelles multivariées ? Une façon de penser est que, puisque l'injustice est causée par les différentes caractéristiques des différentes séquences, si les points communs entre les séquences et les différences entre les séquences peuvent être décomposés et modélisés indépendamment, les problèmes mentionnés ci-dessus peuvent être atténués.
Cet article est basé sur cette idée. L'architecture globale consiste à utiliser la méthode de clustering pour regrouper des séquences multi-variables et à obtenir les caractéristiques communes de chaque groupe ; informations, obtenir des informations publiques. Grâce au processus ci-dessus, les informations publiques et les informations spécifiques à la séquence sont séparées, et la prédiction finale est effectuée sur la base de ces deux parties d'informations.
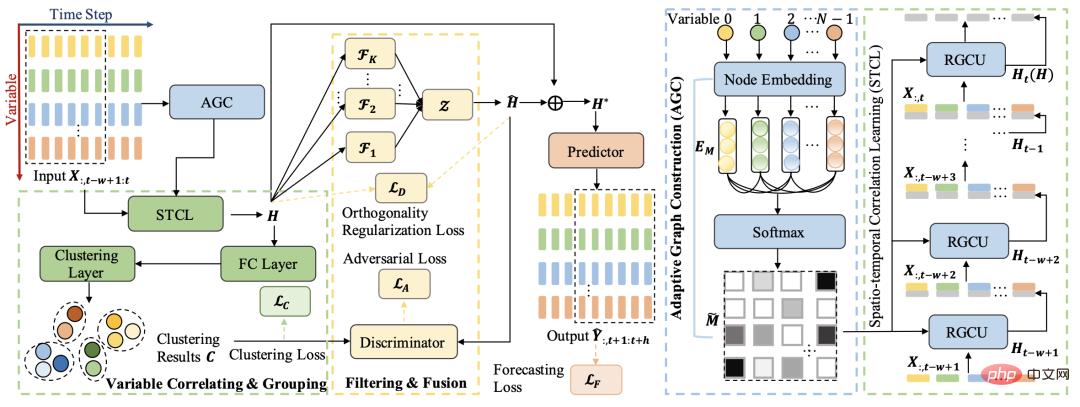
La structure globale du modèle comprend principalement 4 modules : apprentissage des relations de séquence multivariables, réseau de relations spatio-temporelles, regroupement de séquences et apprentissage par décomposition.
L'un des points clés des séries chronologiques multivariées est d'apprendre la relation entre chaque série. Cet article utilise la méthode spatio-temporelle pour apprendre cette relation. Étant donné que les séries chronologiques multivariées ne sont pas comme de nombreuses tâches de prédiction spatio-temporelle, la relation entre diverses variables peut être définie à l'avance, c'est pourquoi la méthode d'apprentissage automatique de la matrice de contiguïté est utilisée ici. La logique de calcul spécifique consiste à générer une intégration initialisée de manière aléatoire pour chaque variable, puis à utiliser le produit interne de l'intégration et un post-traitement pour calculer la relation entre les deux variables en tant qu'éléments aux positions correspondantes de la matrice de contiguïté. La formule est la suivante :
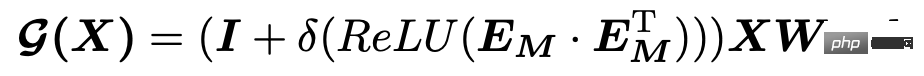
Cette méthode d'apprentissage automatique des matrices de contiguïté est très couramment utilisée dans la prédiction spatio-temporelle, comme le montre Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks (KDD 2020), REST: Reciprocal Framework for La prévision couplée spatio-temporelle (WWW 2021) et d’autres articles ont adopté cette approche. J'ai présenté en détail le principe de mise en œuvre du modèle concerné dans l'article Planet KDD2020, modèle de prédiction espace-temps classique, analyse du code MTGNN. Les étudiants intéressés peuvent lire plus loin.
Avec la matrice de contiguïté, l'article utilise un modèle de prédiction de séries chronologiques graphiques pour encoder spatio-temporellement la série temporelle multivariable afin d'obtenir la représentation de chaque séquence variable. La structure spécifique du modèle est très similaire à DCRNN Basé sur GRU, le module GCN est introduit dans le calcul de chaque unité. On peut comprendre que dans le processus de calcul de chaque unité du GRU normal, le vecteur du nœud voisin est introduit pour faire un GCN afin d'obtenir une représentation mise à jour. Concernant le principe du code d'implémentation du DCRNN, vous pouvez vous référer à l'article Analyse du code source du modèle DCRNN.
Après avoir obtenu la représentation de chaque série temporelle variable, l'étape suivante consiste à regrouper ces représentations pour obtenir le regroupement de chaque séquence variable, puis à extraire les informations uniques de chaque groupe de variables. La fonction de perte suivante est introduite dans cet article pour guider le processus de regroupement, où H représente la représentation de chaque séquence variable et F représente l'affiliation de chaque séquence variable à K catégories.
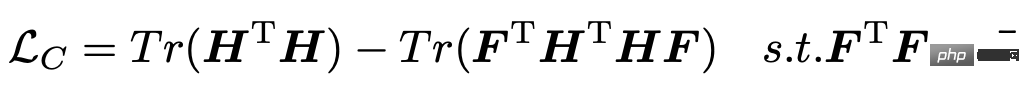
Le processus de mise à jour de cette fonction de perte nécessite l'utilisation de l'algorithme EM, c'est-à-dire la fixation de la séquence pour représenter H, l'optimisation de F, et la fixation de F, l'optimisation de H. La méthode adoptée dans cet article consiste à utiliser SVD pour mettre à jour la matrice F une fois après avoir entraîné plusieurs séries de modèles pour obtenir la représentation H.
Le cœur du module d'apprentissage de la décomposition est de distinguer la représentation publique et la représentation privée de chaque variable de catégorie. La représentation publique fait référence aux caractéristiques partagées par la séquence de variables dans chaque cluster, et la représentation privée fait référence aux caractéristiques partagées par la séquence de variables dans chaque cluster. les caractéristiques au sein de chaque cluster. Caractéristiques propres aux séquences variables. Afin d'atteindre cet objectif, l'article adopte les idées d'apprentissage par décomposition et d'apprentissage contradictoire pour séparer la représentation de chaque cluster de la représentation séquentielle originale. La représentation en cluster représente les caractéristiques de chaque classe et la représentation supprimée représente le point commun de toutes les séquences. L'utilisation de cette représentation commune pour la prédiction peut garantir l'équité dans la prédiction de chaque variable.
L'article utilise l'idée del'apprentissage contradictoire pour calculer directement la distance L2 entre la représentation publique et la représentation privée (c'est-à-dire la représentation de chaque cluster obtenue par clustering), comme une optimisation inverse de perte, de sorte que la représentation publique et la représentation privée L'écart est le plus grand possible. De plus, une contrainte orthogonale sera ajoutée pour rendre le produit interne de la représentation publique et de la représentation privée proche de 0.
Les expériences présentées dans cet article comparent principalement sous deux aspects : l'équité et l'effet de prédiction. Les modèles comparés incluent des modèles de prédiction de séries chronologiques de base (LSTNet, Informer), des modèles de prédiction de séries chronologiques graphiques, etc. En termes d'équité, la variance des résultats de prédiction de différentes variables est utilisée. Grâce à la comparaison, l'équité de cette méthode est considérablement améliorée par rapport à d'autres modèles (comme le montre le tableau ci-dessous).
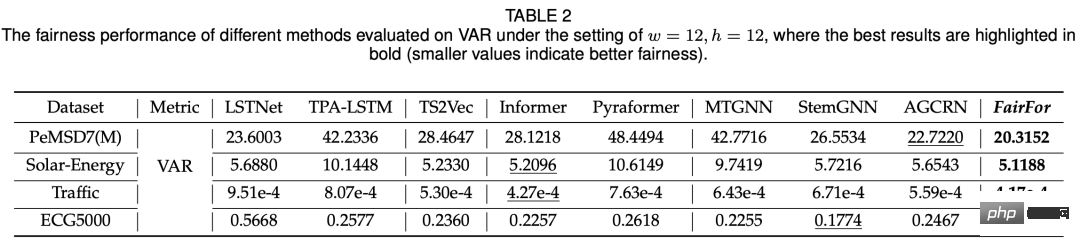
En termes d'effet de prédiction, le modèle proposé dans cet article peut fondamentalement obtenir des résultats équivalents à SOTA :
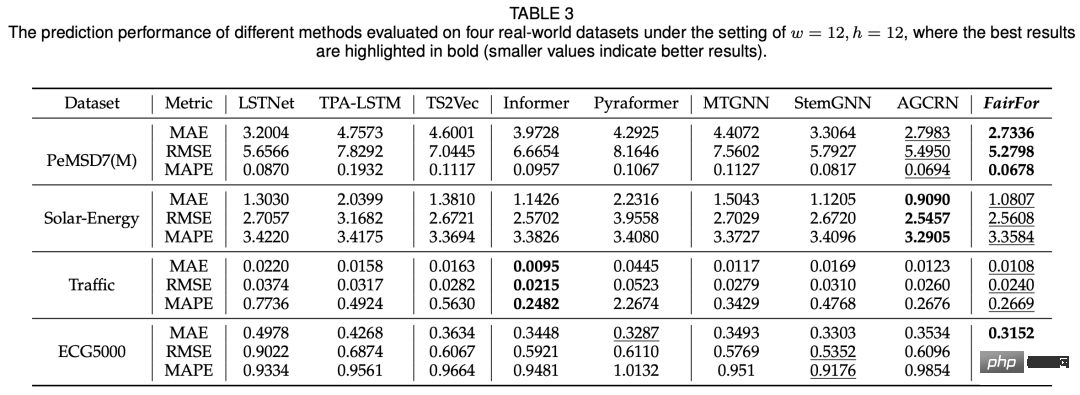
Comment garantir l'équité du modèle est un problème auquel sont confrontés de nombreux scénarios. de l'apprentissage automatique. Cet article introduit cette dimension des problèmes dans la prédiction de séries chronologiques multivariées et utilise des méthodes de prédiction spatio-temporelle et d'apprentissage contradictoire pour mieux la résoudre.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Comment installer WordPress après l'avoir téléchargé
Que signifie l'activité du statut d'activation de Win11 ?
Logiciel de création de site internet
Quelles sont les expressions régulières en php
La différence entre un pointeur de tableau et un tableau de pointeurs
Quels sont les serveurs cloud ?
valeur absolue python
Méthode de mise en œuvre de la fonction VUE page suivante
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
