
Le tas, également connu sous le nom de file d'attente prioritaire, est un arbre binaire complet, et la valeur de chacun de ses nœuds parents ne sera que inférieure ou égale à (les valeurs de) tous les nœuds enfants. Il utilise un tableau pour ce faire : en comptant à partir de zéro, pour tout k , il y a heap[k] . Par souci de comparaison, les éléments inexistants sont considérés comme infinis. La caractéristique la plus intéressante du tas est que le plus petit élément se trouve toujours au nœud racine : heap[0].
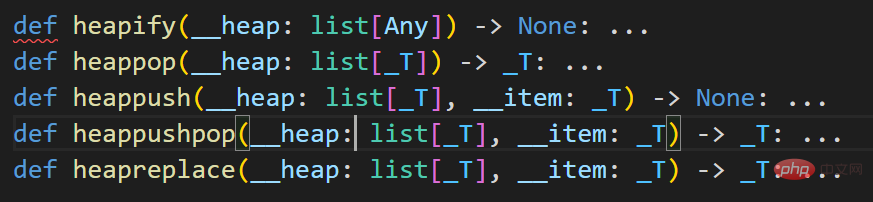
Le tas de Python est généralement un tas minimum, ce qui est différent du contenu de nombreux manuels. La plupart des manuels utilisent un tas maximum. Parce que le tas est exprimé de haut en bas et de gauche à droite, il est donc très similaire à une liste. , pour créer un tas, vous pouvez utiliser une liste pour l'initialiser comme [], ou vous pouvez utiliser une fonction heapify() pour convertir une liste en tas. Voici les opérations liées sur le tas en python. On peut voir que python traite le tas comme une liste.
Ajoutez la valeur de l'élément au tas pour maintenir l'invariance du tas. Il échangera automatiquement les éléments associés selon la fonctionnalité de tas minimum en Python afin que l'élément de nœud racine du tas ne soit jamais plus grand que les éléments de nœud enfant.
Les données originales sont un tas
import heapq h = [1, 2, 3, 5, 7] heapq.heappush(h, 2) print(h) #输出 [1, 2, 2, 5, 7, 3]
Le processus de fonctionnement est le suivant :
1 Ce qui suit est l'état initial
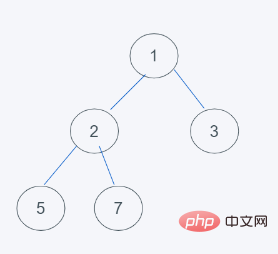
2. Parce qu'il ne répond pas aux caractéristiques minimales du tas, échangez donc avec 3
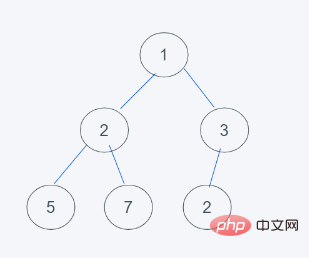
4 Conformément aux caractéristiques du tas minimum, l'échange se termine, le résultat est donc [1, 2, 3, 5, 7, 3]
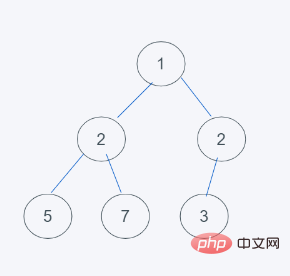 Les données d'origine ne sont pas un tas
Les données d'origine ne sont pas un tas
import heapq h = [5, 2, 1, 4, 7] heapq.heappush(h, 2) print(h) #输出 [5, 2, 1, 4, 7, 2]
heapq.heappop(heap)
pop et renvoie le plus petit élément du tas, en gardant l'immuabilité du tas. Si le tas est vide, lancez IndexError. En utilisant heap[0] , il est possible d'accéder uniquement au plus petit élément sans le faire apparaître.import heapq h = [1, 2, 3, 5, 7] heapq.heappop(h) print(h) #输出 [2, 5, 3, 7]
Le processus de fonctionnement est le suivant :
1 État initial2. au sommet du tas
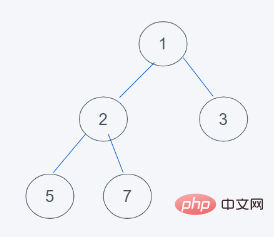
3. Base Échangez des éléments selon les caractéristiques du tas minimum de python Parce que 7>2, échangez 7 et 2
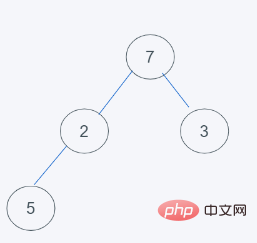
4. tas. Parce que 7>5, échange 7 et 5
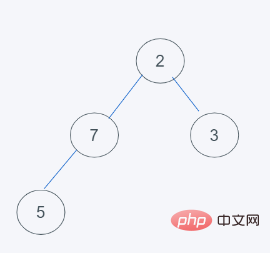
5 . Répond aux exigences du tas, c'est-à-dire que le résultat est [2, 5, 3, 7]
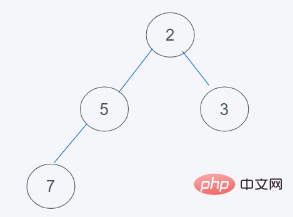 Les données d'origine ne sont pas un tas.
Les données d'origine ne sont pas un tas.
import heapq h = [5, 2, 1, 4, 7] heapq.heappop(h) print(h) [1, 2, 7, 4]
Le processus de fonctionnement est le suivant :
1 L'état initial ne répond évidemment pas aux propriétés du tas2. Supprimez l'élément supérieur (le premier élément) et réorganisez les éléments restants. dans le tas
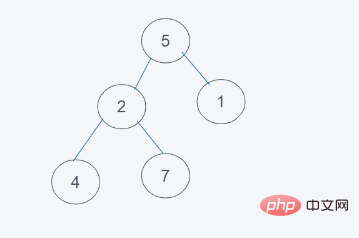
3 Selon les caractéristiques du tas minimum de python, 2>1 échange 2 et 1
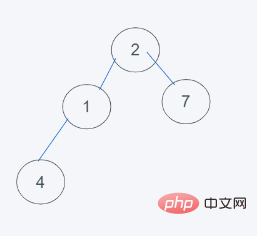
4. 4]
heapq.heappushpop(heap, item)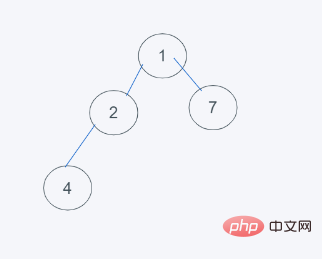
import heapq h = [1, 2, 3, 5, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) #输出 1 [2, 2, 3, 5, 7]
Le processus de fonctionnement est le suivant
1 État initial2.
3.删除最小元素,刚好是堆顶元素1,并使用末尾元素2代替
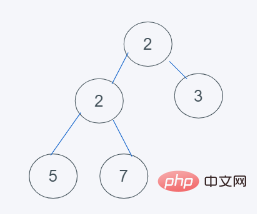
4.符合要求,即结果为[2, 2, 3, 5, 7]
原有数据不是堆
h = [5, 2, 1, 4, 7] min_data = heapq.heappushpop(h, 2) print(min_data) print(h) min_data = heapq.heappushpop(h, 6) print(min_data) print(h) #输出 2 [5, 2, 1, 4, 7] 5 [1, 2, 6, 4, 7]
对于插入元素6的操作过程如下
1.初始状态
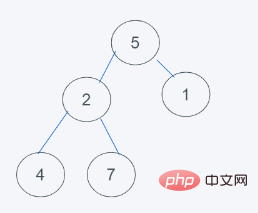
2.插入元素6之后
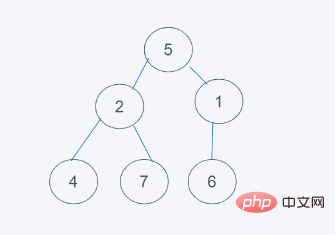
3.发现元素6大于堆顶元素5,弹出堆顶元素5,由堆尾元素6替换
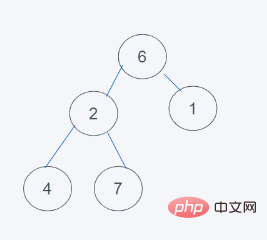
4.依据python的最小堆特性,元素6>元素1且元素6>元素2,但元素2>元素1, 交换6与1
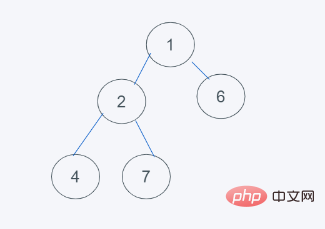
5.符合要求,则结果为[1, 2, 6, 4, 7]
由结果可以看出,当插入元素小于堆顶元素时,则堆不会发生改变,当插入元素大于堆顶元素时,则堆依据python堆的最小堆特性处理。
将列表转换为堆。
h = [1, 2, 3, 5, 7] heapq.heapify(h) print(h) h = [5, 2, 1, 4, 7] heapq.heapify(h) print(h) #输出 [1, 2, 3, 5, 7] [1, 2, 5, 4, 7]
会自动将列表依据python最小堆特性进行重新排列。
弹出并返回最小的元素,并且添加一个新元素item,这个单步骤操作比heappop()加heappush() 更高效。适用于堆元素数量固定的情况。
返回的值可能会比添加的 item 更大。 如果不希望如此,可考虑改用heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个,将较大的值留在堆中。
import heapq h = [1, 2, 3, 5, 7] heapq.heapreplace(h, 6) print(h) h = [5, 2, 1, 4, 7] heapq.heapreplace(h, 6) print(h) #输出 [2, 5, 3, 6, 7] [1, 2, 6, 4, 7]
原有数据是堆
对于插入元素6的操作过程如下:
1.初始状态
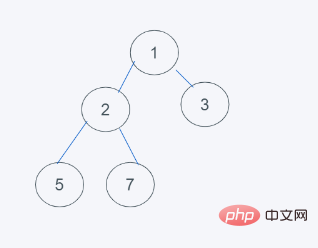
2.弹出最小元素,只能弹出堆顶或者堆尾的元素,很明显,最小元素是1,弹出1,插入元素是6,代替堆顶元素
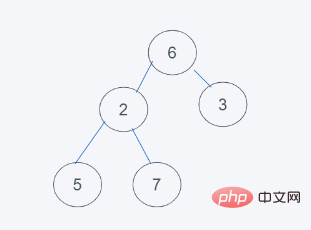
3.依据python堆的最小堆特性,6>2,交换6与2
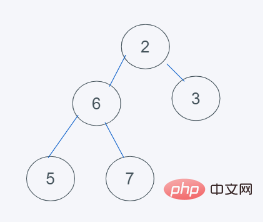
4.依据python堆的最小堆特性,6>5,交换6与5
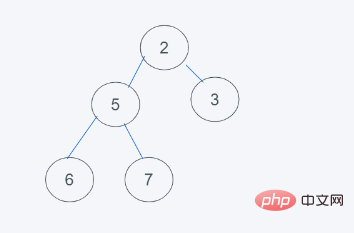
5.符合要求,则结果为[2, 5, 3, 6 ,7]
原有数据不是堆
对于插入元素6的操作过程如下:
1.初始状态
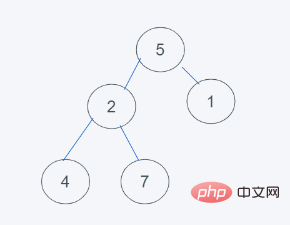
2.对于数据不为堆的情况下,默认移除第一个元素,这里就是元素5,然后插入元素6到堆顶
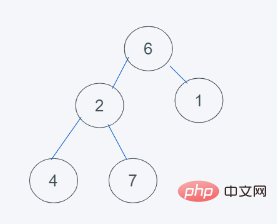
3.依据python的最小堆特性,元素6>1,交换元素6与1
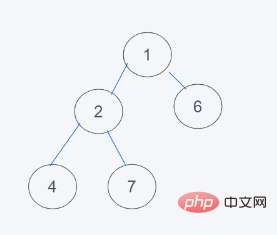
4.符合要求,即结果为[1, 2, 6, 4, 7
将多个已排序的输入合并为一个已排序的输出(例如,合并来自多个日志文件的带时间戳的条目)。 返回已排序值的 iterator。注意需要是已排序完成的可迭代对象(默认为从小到大排序),当reverse为True时,则为从大到小排序。
从 iterable 所定义的数据集中返回前 n 个最大元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数,用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。
等价于: sorted(iterable, key=key, reverse=True)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nlargest(3, h))
for i in range(size):
heapq.nlargest(3, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=True)[:3:])
for i in range(size):
sorted(h, reverse=True)[:3:]
print(time.time() - start)
#输出
[7, 5, 3]
1.6576552391052246
[7, 5, 3]
0.2772986888885498
[7, 5, 4]由上述结构可见,heapq.nlargest与sorted(iterable, key=key, reverse=False)[:n]功能是类似的,但是性能方面还是sorted较为快速。
从 iterable 所定义的数据集中返回前 n 个最小元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数,用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。 等价于: sorted(iterable, key=key)[:n]。
import time
import heapq
h = [1, 2, 3, 5, 7]
size = 1000000
start = time.time()
print(heapq.nsmallest(3, h))
for i in range(size):
heapq.nsmallest(2, h)
print(time.time() - start)
start = time.time()
print(sorted(h, reverse=False)[:3:])
for i in range(size):
sorted(h, reverse=False)[:2:]
print(time.time() - start)
#输出
[1, 2, 3]
1.1738648414611816
[1, 2, 3]
0.2871997356414795由上述结果可见,sorted的性能比后面两个函数都要好,但如果只是返回最大的或者最小的一个元素,则使用max和min最好。
由于在python中堆的特性是最小堆,堆顶的元素始终是最小的,可以将序列转换成堆之后,再使用pop弹出堆顶元素来实现从小到大排序。具体实现如下:
from heapq import heappush, heappop, heapify
def heapsort(iterable):
h = []
for value in iterable:
heappush(h, value)
return [heappop(h) for i in range(len(h))]
def heapsort2(iterable):
heapify(iterable)
return [heappop(iterable) for i in range(len(iterable))]
data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
print(heapsort(data))
print(heapsort2(data))
#输出
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]from heapq import heappush, heappop h = [] heappush(h, (5, 'write code')) heappush(h, (7, 'release product')) heappush(h, (1, 'write spec')) heappush(h, (3, 'create tests')) print(h) print(heappop(h)) [(1, 'write spec'), (3, 'create tests'), (5, 'write code'), (7, 'release product')] (1, 'write spec')
上述操作流程如下:
1.当进行第一次push(5, ‘write code’)时

2.当进行第二次push(7, ‘release product’)时,符合堆的要求
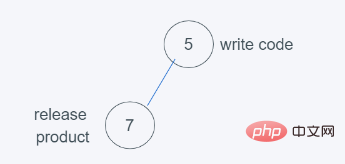
3.当进行第三次push(1, ‘write spec’)时,
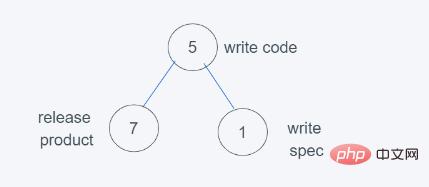
4.依据python的堆的最小堆特性,5>1 ,交换5和1
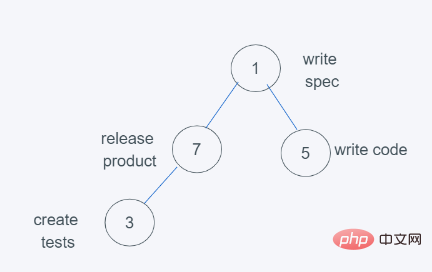
5.当进行最后依次push(3, ‘create tests’)时
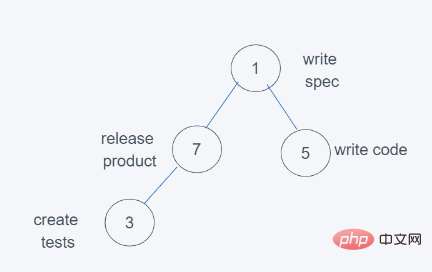
6.依据python堆的最小堆特性,7>3,交换7与3
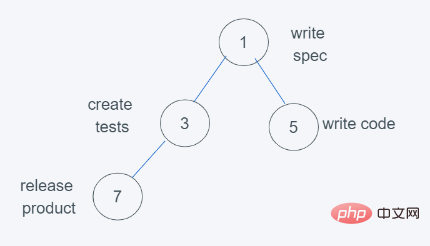
7.符合要求,因此结果为[(1, ‘write spec’), (3, ‘create tests’), (5, ‘write code’), (7, ‘release product’)],弹出元素则是堆顶元素,数字越小,优先级越大。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!