
Un dendrogramme est un diagramme qui montre les relations hiérarchiques entre des objets, des groupes ou des variables. Un dendrogramme se compose de branches connectées à des nœuds ou des clusters qui représentent des groupes d'observations présentant des caractéristiques similaires. La hauteur d'une branche ou la distance entre les nœuds indique à quel point les groupes sont différents ou similaires. Autrement dit, plus les branches sont longues ou plus la distance entre les nœuds est grande, moins les groupes sont similaires. Plus les branches sont courtes ou plus la distance entre les nœuds est petite, plus les groupes sont similaires.
Les dendogrammes sont utiles pour visualiser des structures de données complexes et identifier des sous-groupes ou des groupes de données présentant des caractéristiques similaires. Ils sont couramment utilisés en biologie, en génétique, en écologie, en sciences sociales et dans d'autres domaines où les données peuvent être regroupées en fonction de leur similarité ou de leur corrélation.
Connaissances de base :
Le mot "dendrogramme" vient des mots grecs "dendron" (arbre) et "gramma" (dessin). En 1901, le mathématicien et statisticien britannique Karl Pearson a utilisé un diagramme en arbre pour montrer la relation entre différentes espèces végétales [1]. Il a appelé ce graphique un « graphique de cluster ». Cela peut être considéré comme la première utilisation des dendrogrammes.
Nous utiliserons les cours réels des actions de plusieurs entreprises pour le regroupement. Pour un accès facile, les données sont collectées à l'aide de l'API gratuite fournie par Alpha Vantage. Alpha Vantage fournit à la fois une API gratuite et une API premium. L'accès via l'API nécessite une clé, veuillez vous référer à son site Web.
import pandasaspd
import requests
companies={'Apple':'AAPL','Amazon':'AMZN','Facebook':'META','Tesla':'TSLA','Alphabet (Google)':'GOOGL','Shell':'SHEL','Suncor Energy':'SU',
'Exxon Mobil Corp':'XOM','Lululemon':'LULU','Walmart':'WMT','Carters':'CRI','Childrens Place':'PLCE','TJX Companies':'TJX',
'Victorias Secret':'VSCO','MACYs':'M','Wayfair':'W','Dollar Tree':'DLTR','CVS Caremark':'CVS','Walgreen':'WBA','Curaleaf':'CURLF'}20 entreprises sélectionnées dans les secteurs de la technologie, de la vente au détail, du pétrole et du gaz et d'autres secteurs.
import time
all_data={}
forkey,valueincompanies.items():
# Replace YOUR_API_KEY with your Alpha Vantage API key
url=f'https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol={value}&apikey=<YOUR_API_KEY>&outputsize=full'
response=requests.get(url)
data=response.json()
time.sleep(15)
if'Time Series (Daily)'indataanddata['Time Series (Daily)']:
df=pd.DataFrame.from_dict(data['Time Series (Daily)'], orient='index')
print(f'Received data for {key}')
else:
print("Time series data is empty or not available.")
df.rename(columns= {'1. open':key}, inplace=True)
all_data[key]=df[key]Le code ci-dessus définit une pause de 15 secondes entre les appels d'API pour garantir qu'il n'est pas bloqué trop fréquemment.
# find common dates among all data frames
common_dates=None
fordf_key, dfinall_data.items():
ifcommon_datesisNone:
common_dates=set(df.index)
else:
common_dates=common_dates.intersection(df.index)
common_dates=sorted(list(common_dates))
# create new data frame with common dates as index
df_combined=pd.DataFrame(index=common_dates)
# reindex each data frame with common dates and concatenate horizontally
fordf_key, dfinall_data.items():
df_combined=pd.concat([df_combined, df.reindex(common_dates)], axis=1)Intégrez les données ci-dessus dans le DF dont nous avons besoin, qui peut être utilisé directement ci-dessous
Le clustering hiérarchique est un algorithme de clustering utilisé pour l'apprentissage automatique et l'analyse des données. Il utilise une hiérarchie de clusters imbriqués pour regrouper des objets similaires en clusters en fonction de leur similarité. L'algorithme peut être aggloméré, en commençant par des objets uniques et en les fusionnant en clusters, ou divisif, en commençant par un grand cluster et en le divisant de manière récursive en clusters plus petits.
Il convient de noter que toutes les méthodes de clustering ne sont pas des méthodes de clustering hiérarchiques et que les dendrogrammes ne peuvent être utilisés que sur quelques algorithmes de clustering.
Algorithme de clustering Nous utiliserons le clustering hiérarchique fourni dans le module scipy.
1. Clustering descendant
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform top-down clustering clustering=sch.linkage(dist_mat, method='complete') cuts=sch.cut_tree(clustering, n_clusters=[3, 4]) # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Top-Down Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
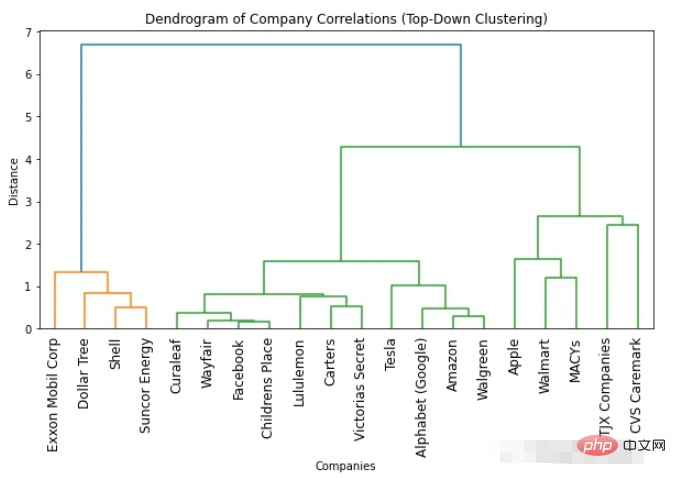
Comment déterminer le nombre optimal de clusters en fonction du dendrogramme
Le moyen le plus simple de trouver le nombre optimal de clusters est de regarder le dendrogramme généré utilisé. nombre de couleurs. Le nombre optimal de clusters est inférieur d’un au nombre de couleurs. Ainsi, d’après le dendrogramme ci-dessus, le nombre optimal de clusters est de deux.
Une autre façon de trouver le nombre optimal de clusters consiste à identifier les points où la distance entre les clusters change soudainement. C'est ce qu'on appelle le « point du genou » ou « le point du coude » et peut être utilisé pour déterminer le nombre de clusters qui capture le mieux la variation des données. Nous pouvons voir dans la figure ci-dessus que le changement de distance maximal entre différents nombres de clusters se produit entre 1 et 2 clusters. Encore une fois, le nombre optimal de clusters est de deux.
Obtenez n'importe quel nombre de clusters à partir d'un dendrogramme
L'un des avantages de l'utilisation d'un dendrogramme est que les objets peuvent être regroupés en n'importe quel nombre de clusters en regardant le dendrogramme. Par exemple, si vous devez trouver deux clusters, vous pouvez regarder la ligne verticale supérieure du dendrogramme et décider des clusters. Par exemple, dans cet exemple, si deux clusters sont requis, il y a alors quatre sociétés dans le premier cluster et 16 sociétés dans le deuxième cluster. Si nous avons besoin de trois clusters, nous pouvons diviser le deuxième cluster en 11 et 5 entreprises. Si vous avez besoin de plus, vous pouvez suivre cet exemple.
2. Clustering ascendant
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform bottom-up clustering clustering=sch.linkage(dist_mat, method='ward') # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Bottom-Up Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
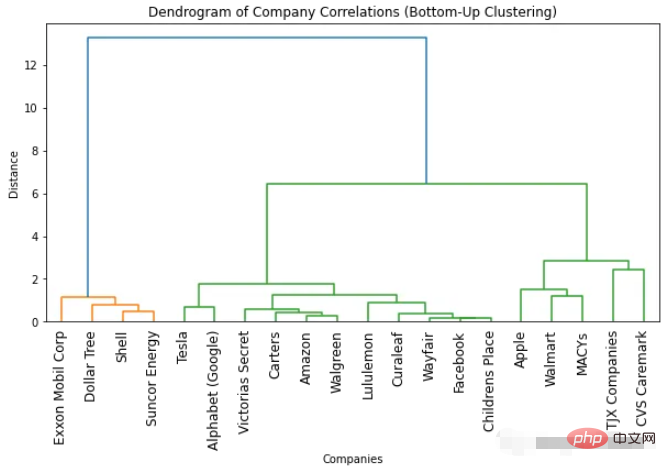
Le dendrogramme que nous obtenons pour le clustering ascendant est similaire au clustering descendant. Le nombre optimal de clusters est toujours de deux (en fonction du nombre de couleurs et de la méthode du « point d'inflexion »). Mais si nous avons besoin de plus de clusters, des différences subtiles seront observées. Ceci est normal car les méthodes utilisées sont différentes, ce qui entraîne de légères différences dans les résultats.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!