
L'algorithme de tri consiste à factoriser un ou plusieurs groupes des données sont réorganisées selon un modèle défini. La séquence finale est présentée selon certaines règles.
Dans les algorithmes de tri, la stabilité et l'efficacité sont des enjeux que nous devons souvent prendre en compte.
Stabilité : La stabilité signifie que lorsque deux éléments identiques apparaissent dans une séquence en même temps, après un certain algorithme de tri, les positions relatives des deux avant et après le tri ne changent pas.
Analyse de complexité :
(1) Complexité temporelle : de l'état initial de la séquence au résultat final trié après des opérations telles que transformation et décalage de l'algorithme de tri Une mesure du temps consacré au processus d’un État.
(2) Complexité spatiale : il s'agit de la surcharge spatiale dépensée depuis l'état initial de la séquence en passant par le processus de tri et de transformation de déplacement jusqu'à l'état final.
Les algorithmes de tri courants sont divisés dans les types suivants :
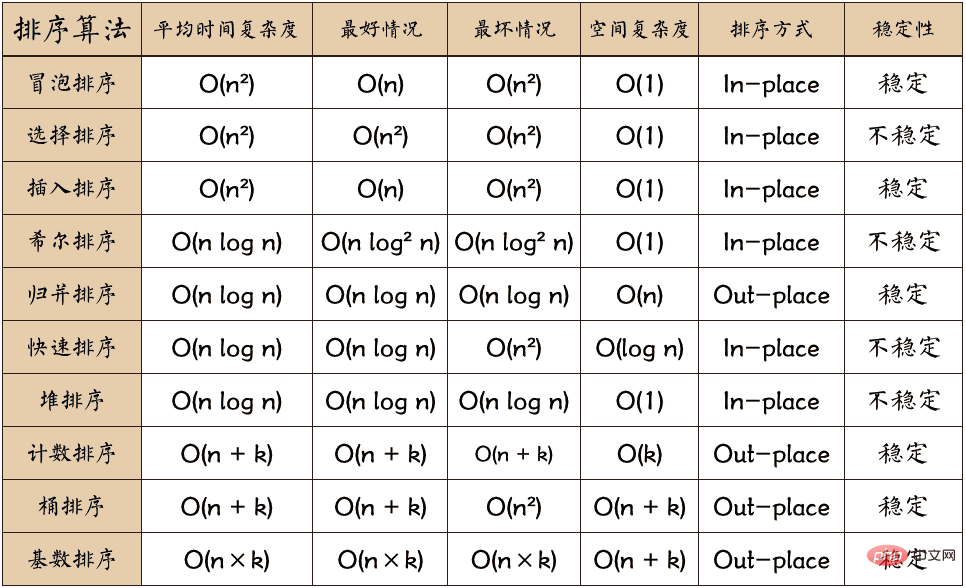
Binary Insertion Sort est une amélioration de l'algorithme de tri par insertion. Insérez continuellement des éléments dans la séquence précédemment triée. Puisque la première moitié est une séquence triée, nous n'avons pas besoin de rechercher le point d'insertion dans l'ordre. Nous pouvons utiliser la méthode de demi-recherche pour accélérer la recherche du point d'insertion.
Dans le processus d'insertion d'un nouvel élément dans le tableau trié, lors de la recherche du point d'insertion, définissez le premier élément de la zone à insérer sur un [ low], le dernier élément est mis à a[high], puis à chaque tour de comparaison, l'élément à insérer est comparé à a[m], où m = (low+high)/2, s'il est plus petit que l'élément de référence, sélectionnez a[ low] à a[m-1] sont la nouvelle zone d'insertion (c'est-à-dire high=m-1), sinon sélectionnez a[m+1] à a[high] comme nouvelle zone d'insertion ( c'est-à-dire low=m+1), cela continue jusqu'à ce que low
En bref : profitez des caractéristiques d'ordonnancement des éléments disposés et utilisez les caractéristiques de demi-recherche pour trouver rapidement la position à insérer.
// Binary Insertion Sort method
private static void binaryInsertSort(int[] array){
for(int i = 1; i < array.length; i++){
int temp = array[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < array[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
array[j] = array[j - 1];
}
array[low] = temp;
}
}L'algorithme de tri par demi-insertion est un algorithme de tri stable Par rapport à l'algorithme d'insertion directe, il réduit considérablement le nombre de comparaisons entre les mots-clés, c'est donc le cas. plus rapide que L'algorithme de tri par insertion directe est rapide, mais le nombre de déplacements d'enregistrement n'a pas changé, donc la complexité temporelle de l'algorithme de tri par demi-insertion est toujours O(n^2), ce qui est la même que l'algorithme de tri par insertion directe.
Complexité temporelle
Meilleur des cas : O(n). Si les éléments sont triés dans l'ordre direct, la position sera trouvée directement au début, sans recherche ni décalage.
Pire des cas : O(n^2). Si les éléments sont triés dans l’ordre inverse, une recherche de données est requise à chaque fois.
Complexité moyenne : O(n^2).
Complexité spatiale : O(1). Seuls quelques espaces de stockage sont nécessaires pour enregistrer les unités d'information clés, c'est-à-dire que la complexité spatiale est O(1).
Exemple :
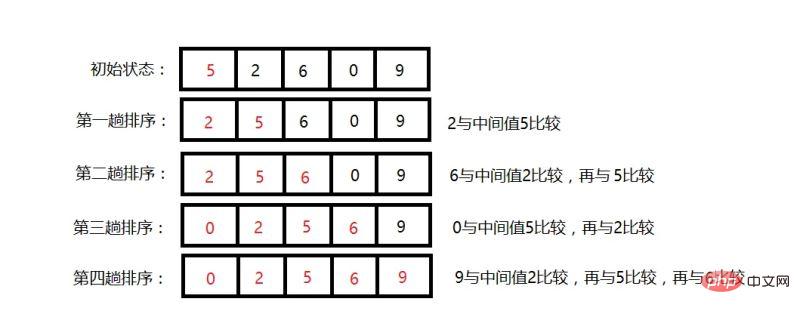
L'idée générale de l'algorithme a été décrit ci-dessus, utilisons un exemple directement pour tester l'eau.
tri par insertion réduit de moitié
Description du problème :
Vous recevez un tableau de nombres entiers, veuillez trier le tableau par ordre croissant.
Exemple 1 :
Entrée : nums = [5,2,3,1]
Sortie : [1,2,3,5 ]
Exemple 2 :
Entrée : nums = [5,1,1,2,0,0]
Sortie : [0, 0,1,1,2,5]
Astuce :
1 <= nums.length <= 5 * 104
- 5 * 104 <= nums[i] <= 5 * 104
class Solution {
public int[] sortArray(int[] nums) {
for(int i = 1; i < nums.length; i++){
int temp = nums[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < nums[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
nums[j] = nums[j - 1];
}
nums[low] = temp;
}
return nums;
}
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!