Analyse d'exemples de complexité temporelle et spatiale Java
1. Efficacité des algorithmes
L'analyse de l'efficacité des algorithmes est divisée en deux types : le premier est l'efficacité temporelle et le second est l'efficacité spatiale. L’efficacité temporelle est appelée complexité temporelle, et l’efficacité spatiale est appelée complexité spatiale. La complexité temporelle mesure principalement la vitesse d'exécution d'un algorithme, tandis que la complexité spatiale mesure principalement l'espace supplémentaire requis par un algorithme. Au début du développement informatique, la capacité de stockage des ordinateurs était très faible. Nous nous soucions donc beaucoup de la complexité de l’espace. Cependant, après le développement rapide de l’industrie informatique, la capacité de stockage des ordinateurs a atteint un niveau très élevé. Nous n’avons donc plus besoin de prêter une attention particulière à la complexité spatiale d’un algorithme.
2. Complexité temporelle
1. Concept de complexité temporelle
Le temps que prend un algorithme est proportionnel au nombre d'exécutions de ses instructions. Le nombre d'exécutions d'opérations de base dans l'algorithme est la complexité temporelle de l'algorithme. C'est-à-dire que lorsque nous obtenons un code et examinons la complexité temporelle du code, nous trouvons principalement combien de fois le code avec les instructions les plus exécutées dans le code a été exécuté.
2. Représentation asymptotique du grand O
Regardez l'image et analysez :

Lorsque la valeur de N devient de plus en plus grande, les valeurs de 2N et 10 peuvent être ignorées.
En fait, lorsque nous calculons la complexité temporelle, nous n'avons pas réellement à calculer le nombre exact d'exécutions, mais seulement le nombre approximatif d'exécutions, nous utilisons donc ici la représentation asymptotique de Big O.
Notation Big O : C'est un symbole mathématique utilisé pour décrire le comportement asymptotique d'une fonction.
1. Remplacez toutes les constantes additives au moment de l'exécution par la constante 1.
2. Dans la fonction des temps d'exécution modifiés, seul le terme d'ordre le plus élevé est conservé.
3. Si le terme d'ordre le plus élevé existe et n'est pas 1, supprimez la constante multipliée par ce terme. Le résultat est l’ordre Big O.

Grâce à ce qui précède, nous constaterons que la représentation asymptotique de Big O supprime les éléments qui ont peu d'impact sur les résultats et exprime le nombre d'exécutions de manière concise et claire.
De plus, il existe des cas meilleurs, moyens et pires pour la complexité temporelle de certains algorithmes :
Pire cas : le nombre maximum d'exécutions (limite supérieure) pour toute taille d'entrée
Cas moyen : le nombre d'exécutions attendu pour n'importe quelle taille d'entrée
Meilleur cas : Nombre minimum d'exécutions (limite inférieure) pour n'importe quelle taille d'entrée
Par exemple : Recherche d'une donnée Situation : N/2 fois trouvées
En pratique, la situation générale se concentre sur la pire situation de fonctionnement de l'algorithme, donc la complexité temporelle de la recherche de données dans le tableau est O(N)
Complexité temporelle du calcul
Exemple 1 :
L'opération de base a été exécutée 2N+10 fois en dérivant le grand. O méthode de commande, on sait que la complexité temporelle est O(N)Exemple 2 :

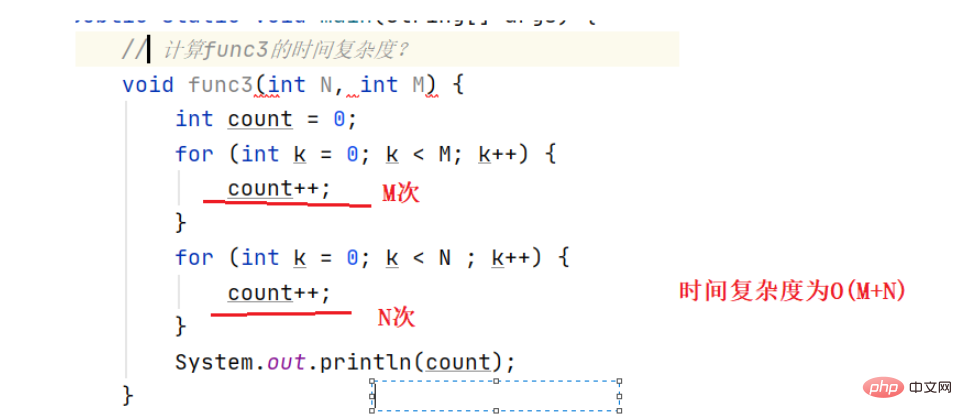


 Complexité temporelle de la récursion = Nombre de récursions * Nombre de fois que chaque récursion est exécutée
Complexité temporelle de la récursion = Nombre de récursions * Nombre de fois que chaque récursion est exécutée

.
Grâce au calcul et à l'analyse, nous avons constaté que l'opération de base est récursive 2^N fois et que la complexité temporelle est O(2^N).
Règle :
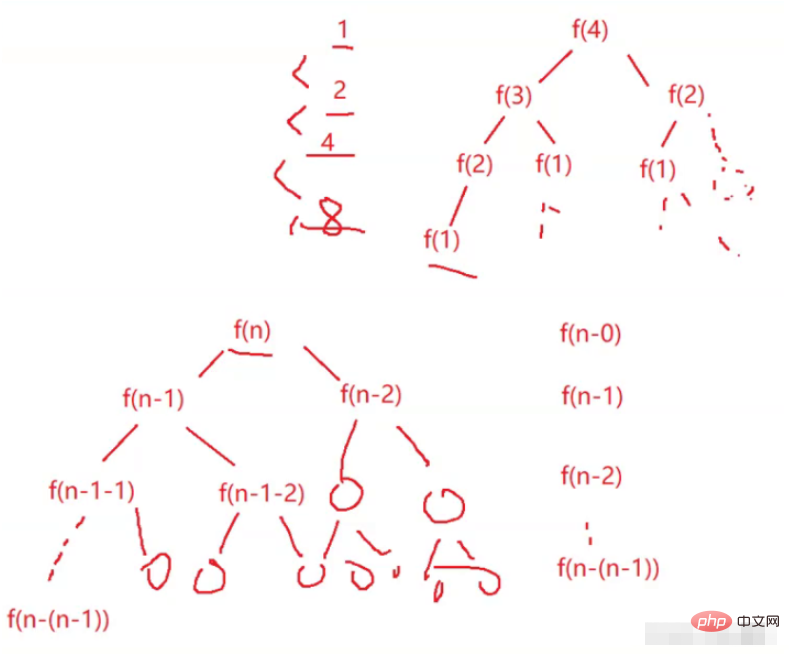
2^0+2^1+2^2+2^3……2^(n-(n-1))
Somme d'une séquence géométrique
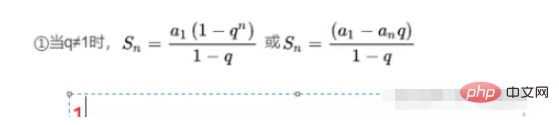
a1 représente le premier élément, q est égal à 2, 1(1-2^n)/-1, ce qui équivaut à 2^n+1, donc la complexité temporelle est O(2^n)
Trois.
La complexité spatiale est une mesure de la quantité d'espace de stockage qu'un algorithme occupe temporairement pendant son fonctionnement. La complexité spatiale n'est pas le nombre d'octets d'espace occupés par le programme, car cela n'a pas beaucoup de sens, donc la complexité spatiale est calculée par le nombre de variables. Les règles de calcul de la complexité spatiale sont fondamentalement similaires à la complexité pratique, et la notation asymptotique grand O est également utilisée.
Exemple 1 : Calculer la complexité spatiale du tri à bulles
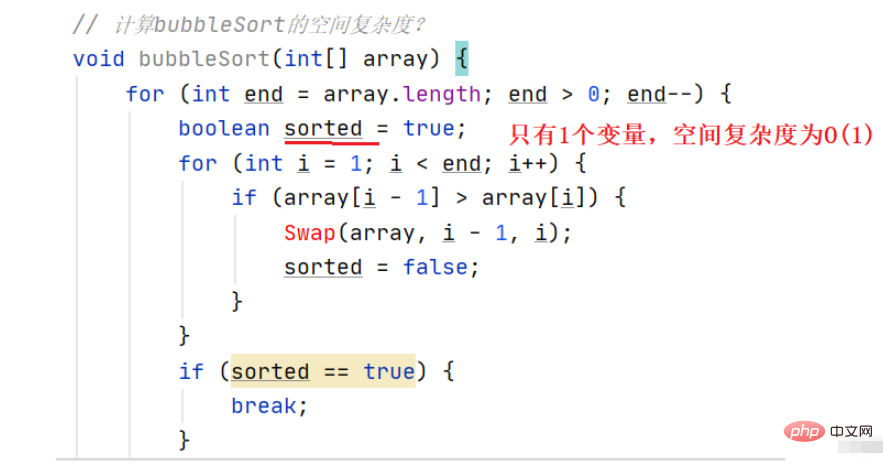
utilise un espace supplémentaire constant, donc la complexité spatiale est O(1)
Exemple 2 : Calculer la complexité spatiale de Fibonacci
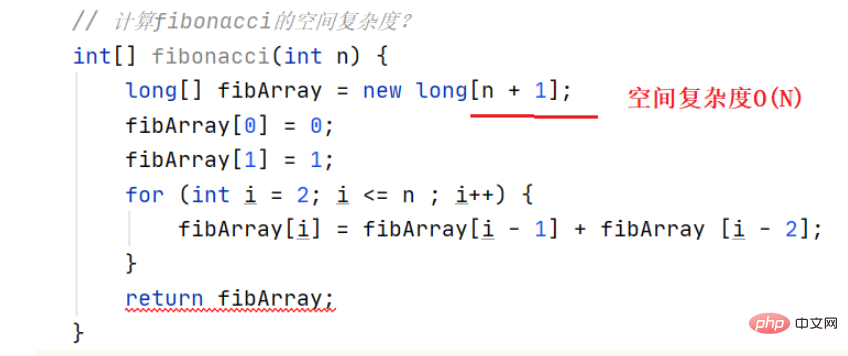
N espaces sont ouverts dynamiquement et la complexité spatiale est O(N)
Exemple 3 : Calculez la complexité spatiale de la récursion factorielle

L'appel récursif est effectué N fois et N cadres de pile sont ouverts, chaque cadre de pile utilise un quantité d'espace constante. La complexité spatiale est O(N)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Racine carrée en Java
Aug 30, 2024 pm 04:26 PM
Guide de la racine carrée en Java. Nous discutons ici du fonctionnement de Square Root en Java avec un exemple et son implémentation de code respectivement.
 Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre parfait en Java. Nous discutons ici de la définition, comment vérifier le nombre parfait en Java ?, des exemples d'implémentation de code.
 Numéro Armstrong en Java
Aug 30, 2024 pm 04:26 PM
Numéro Armstrong en Java
Aug 30, 2024 pm 04:26 PM
Guide du numéro Armstrong en Java. Nous discutons ici d'une introduction au numéro d'Armstrong en Java ainsi que d'une partie du code.
 Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Générateur de nombres aléatoires en Java
Aug 30, 2024 pm 04:27 PM
Guide du générateur de nombres aléatoires en Java. Nous discutons ici des fonctions en Java avec des exemples et de deux générateurs différents avec d'autres exemples.
 Weka en Java
Aug 30, 2024 pm 04:28 PM
Weka en Java
Aug 30, 2024 pm 04:28 PM
Guide de Weka en Java. Nous discutons ici de l'introduction, de la façon d'utiliser Weka Java, du type de plate-forme et des avantages avec des exemples.
 Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre de Smith en Java. Nous discutons ici de la définition, comment vérifier le numéro Smith en Java ? exemple avec implémentation de code.
 Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Dans cet article, nous avons conservé les questions d'entretien Java Spring les plus posées avec leurs réponses détaillées. Pour que vous puissiez réussir l'interview.
 Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Java 8 présente l'API Stream, fournissant un moyen puissant et expressif de traiter les collections de données. Cependant, une question courante lors de l'utilisation du flux est: comment se casser ou revenir d'une opération FOREAK? Les boucles traditionnelles permettent une interruption ou un retour précoce, mais la méthode Foreach de Stream ne prend pas directement en charge cette méthode. Cet article expliquera les raisons et explorera des méthodes alternatives pour la mise en œuvre de terminaison prématurée dans les systèmes de traitement de flux. Lire plus approfondie: Améliorations de l'API Java Stream Comprendre le flux Forach La méthode foreach est une opération terminale qui effectue une opération sur chaque élément du flux. Son intention de conception est






