
Dans notre vie d'aujourd'hui, des exemples de graphiques incluent les réseaux sociaux, tels que Twitter, Mastodon et tout réseau de citations reliant articles et auteurs, les molécules, les graphiques de connaissances, tels que les diagrammes UML, les encyclopédies et les sites Web avec des hyperliens, des représentations des phrases aux des arbres syntaxiques à n'importe quelle grille 3D, on peut dire que les graphiques sont partout.
Récemment, Clémentine Fourrier, chercheuse chez Hugging Face, a présenté l'apprentissage automatique des graphes, omniprésent aujourd'hui, dans l'article "Introduction à l'apprentissage automatique des graphes". Que sont les graphiques ? Pourquoi utiliser des graphiques ? Comment représenter au mieux un graphique ? Comment les gens apprennent-ils à partir des graphiques ? Clémentine Fourrier a souligné qu'un graphe est une description d'éléments liés par des relations. Parmi eux, des méthodes pré-neurales aux réseaux de neurones graphiques, les méthodes d'apprentissage des graphes sont encore couramment utilisées.
De plus, certains chercheurs ont récemment commencé à envisager d'appliquer des Transformers aux graphiques. Les Transformers ont une bonne évolutivité et peuvent atténuer certaines des limitations de GNN, et les perspectives sont très prometteuses.
Essentiellement, le diagramme est une description des éléments liés par la relation. Les éléments d'un graphe (ou d'un réseau) sont appelés nœuds (ou sommets) et sont reliés par des arêtes (ou des liens). Par exemple, dans un réseau social, les nœuds sont des utilisateurs et les bords sont des connexions entre utilisateurs ; dans les molécules, les nœuds sont des atomes et les bords sont leurs liaisons moléculaires.
Comme vous pouvez le voir, lorsque vous utilisez des données, vous devez d'abord considérer leur représentation optimale, y compris homogène/hétérogène. , Directionnel/non dirigé, etc.
Au niveau des graphiques, les tâches principales sont les suivantes :
La couche de nœuds est généralement la prédiction Utiliser la prédiction des attributs de nœuds pour prédire les coordonnées 3D des atomes à partir du graphique global d'une molécule, et donc la façon dont la molécule se plie dans l'espace 3D, est un problème de biochimie difficile.
La prédiction des bords inclut la prédiction des attributs de bord et la prédiction des bords manquants. La prédiction des attributs de bord aide à prédire les effets secondaires des médicaments, étant donné les effets secondaires indésirables d'une paire de médicaments ; la prédiction des bords manquants est utilisée dans les systèmes de recommandation pour prédire si deux nœuds du graphique sont liés.
Au niveau du sous-graphe, une détection de communauté ou une prédiction d'attribut de sous-graphe peut être effectuée. Les réseaux sociaux peuvent utiliser la détection de communauté pour déterminer comment les personnes sont connectées. La prédiction des attributs de sous-graphe est souvent utilisée dans les systèmes d'itinéraire, tels que Google Maps, qui peuvent être utilisés pour prédire les heures d'arrivée estimées.
Lorsqu'il s'agit de prédire l'évolution d'un graphique spécifique, tout ce qui concerne la configuration de la transformation, y compris la formation, la validation et les tests, peut être effectué sur le même graphique. Mais créer des ensembles de données de formation, d'évaluation ou de test à partir d'un seul graphique n'est pas facile, et beaucoup de travail est effectué à l'aide de différents graphiques (séparations de formation/évaluation/test séparées), ce que l'on appelle un paramètre d'induction.
Il existe deux manières courantes de représenter le traitement et les opérations d'un graphe, soit comme un ensemble de toutes ses arêtes (éventuellement complété par un ensemble de tous ses nœuds), soit comme une matrice d'adjacence entre tous ses nœuds. Parmi eux, la matrice de contiguïté est une matrice carrée (taille du nœud × taille du nœud) indiquant quels nœuds sont directement connectés aux autres nœuds. Notez que comme la plupart des graphiques ne sont pas densément connectés, le fait d'avoir une matrice de contiguïté clairsemée rend le calcul plus difficile.
Les graphiques sont très différents des objets typiques utilisés en ML, en raison de leur topologie plus complexe que les « séquences » (comme le texte et l'audio) ou les « grilles ordonnées » (comme les images et les vidéos) : même s'ils peuvent être représenté sous forme de liste ou de matrice, mais cette représentation ne peut pas être considérée comme un objet ordonné. Autrement dit, si vous brouillez les mots d’une phrase, vous créez une nouvelle phrase, et si vous brouillez une image et réorganisez ses colonnes, vous créez une nouvelle image.
Remarque : le logo Hugging Face et le logo Hugging Face perturbé sont complètement différents La nouvelle image de
Mais ce n'est pas le cas du graphe : si on lave la liste des bords ou les colonnes de la matrice d'adjacence du graphe, cela c'est toujours le même graphique.
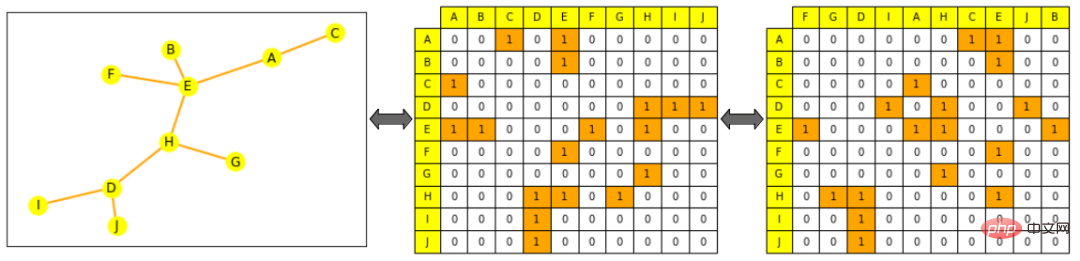
Remarque : Sur la gauche se trouve un petit diagramme, le jaune représente les nœuds, l'orange représente les arêtes ; centre La matrice de contiguïté sur l'image, les colonnes et les lignes sont disposées par ordre alphabétique des nœuds : la ligne du nœud A (la première ligne) peut être vue comme étant connectée à E et C, l'image de droite a la matrice de contiguïté brouillée ; (les colonnes ne sont plus par ordre alphabétique), C'est toujours une représentation valide du graphique, c'est-à-dire que A est toujours connecté à E et C 🎜🎜#Le processus normal d'utilisation de l'apprentissage automatique pour traiter les graphiques est pour générer d'abord une représentation significative pour le projet, où les nœuds, les arêtes ou le graphique complet dépendent des exigences spécifiques de la tâche, et pour former des prédicteurs pour la tâche cible. Comme pour les autres modèles, vous pouvez contraindre la représentation mathématique d'un objet afin qu'il soit mathématiquement proche d'un objet similaire. Mais à l’intérieur de cela, la similarité est difficile à définir strictement dans le graphe ML : par exemple, deux nœuds sont-ils plus similaires lorsqu’ils ont la même étiquette ou les mêmes voisins ?
approche neuronale frontale
Utiliser simplement les fonctionnalités d'ingénierie
#🎜 🎜 #Les fonctionnalités au niveau du nœud peuvent fournir des informations sur l'importance ainsi que des informations basées sur la structure et les combiner.
La centralité des nœuds peut être utilisée pour mesurer l'importance des nœuds dans le graphique, calculée récursivement en additionnant la centralité voisine de chaque nœud jusqu'à convergence, ou par la métrique de distance la plus courte est calculé de manière récursive, le degré du nœud est le nombre de voisins directs qu'il possède ; le coefficient de regroupement mesure le degré de connexion des voisins du nœud ; le calcul vectoriel du degré des Graphlets peut calculer combien de graphlets différents ont un nœud donné comme racine, où, les graphlets peuvent créer tous les minigraphes en utilisant un nombre donné de nœuds connectés.
Remarque : petit graphique de 2 à 5 nœuds# 🎜 🎜#
Les fonctionnalités de niveau Edge sont complétées par des informations plus détaillées sur la connectivité des nœuds, y compris la distance la plus courte entre deux nœuds, leurs voisins communs et l'indice de Katz (appelé nombre de chemins possibles de une certaine longueur entre deux nœuds - qui peut être calculée directement à partir de la matrice de contiguïté). 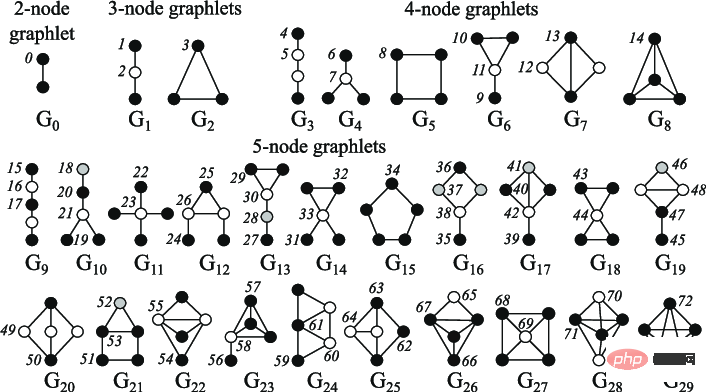
Les fonctionnalités au niveau du graphique contiennent des informations de haut niveau sur les similitudes et les particularités des graphiques, où le nombre de sous-graphes, bien que coûteux en termes de calcul, fournit des informations sur les formes des sous-graphes. La méthode de base mesure la similarité entre les graphiques via différentes méthodes de « sac de nœuds » (similaires au sac de mots).
La méthode basée sur la marche utilise une marche aléatoire pour visiter le nœud j à partir de nœud i Les probabilités sont utilisées pour définir des mesures de similarité, et ces méthodes combinent des informations locales et globales. Par exemple, auparavant, Node2Vec simulait des marches aléatoires entre les nœuds du graphique, en utilisant des sauts de grammes pour traiter ces marches, tout comme nous le faisons avec des mots dans des phrases pour calculer des intégrations.
Ces méthodes peuvent également être utilisées pour accélérer le calcul de la méthode PageRank, qui attribue un score d'importance à chaque nœud en fonction de ses connexions avec d'autres nœuds, par ex. Marche aléatoire pour évaluer sa fréquence de visites. Cependant, les méthodes ci-dessus présentent également certaines limites. Elles ne peuvent pas obtenir l'intégration de nouveaux nœuds, ne peuvent pas bien capturer la similarité structurelle entre les nœuds et ne peuvent pas utiliser de fonctionnalités ajoutées.
Les réseaux de neurones peuvent se généraliser à des données invisibles. Compte tenu des contraintes de représentation mentionnées précédemment, comment un bon réseau de neurones doit-il gérer les graphiques ?
Ce qui suit présente deux méthodes :
Un GNN est composé de couches consécutives. Une couche GNN représente un nœud comme une combinaison de la représentation de ses voisins et de lui-même de la couche précédente (passage de message), souvent avec des activations ajoutées pour ajouter une certaine non-linéarité. Par rapport à d'autres modèles, CNN peut être considéré comme un GNN avec une taille de voisin fixe (par fenêtre coulissante) et un ordre (équivariance sans permutation) tandis que Transformer sans intégration de position peut être considéré comme un GNN sur un graphe d'entrée entièrement connecté ;
Agrégation et messagerie
Graph Convolutional Networks, qui fait la moyenne des représentations normalisées des nœuds voisins #🎜🎜 ##🎜🎜 ; #
Graph Attention Networks, apprenez à peser différents voisins (tels que Transformer) en fonction de leur importance
Graphique des réseaux d'isomorphisme, en appliquant MLP aux nœuds voisins Agréger la représentation par la somme des représentations.
A chaque nouvelle couche, la représentation des nœuds comprend de plus en plus de nœuds. Un nœud passe par le premier niveau, une agrégation de ses voisins directs. Grâce à la deuxième couche, il s'agit toujours d'une agrégation de ses voisins immédiats, mais sa représentation inclut désormais également ses propres voisins (de la première couche). Après n niveaux, la représentation de tous les nœuds devient l'ensemble de tous ses voisins à distance n, et donc une agrégation du graphe complet si son diamètre est inférieur à n.
S'il y a trop de couches de réseau, il y a un risque que chaque nœud devienne une agrégation du graphe complet (et la représentation des nœuds converge vers la même représentation pour tous les nœuds), c'est ce qu'on appelle le problème de sur-lissage et peut être résolu par Solution :
Le problème du sur-lissage est un domaine de recherche important dans le graph ML, car cela empêche les GNN de se développer, comme les transformateurs ont été prouvés dans d'autres modèles.
Le transformateur sans couche de codage de position est invariant par permutation, et Transformer a également une bonne évolutivité, les chercheurs ont donc récemment commencé à envisager d'appliquer des transformateurs aux graphiques. La plupart des méthodes se concentrent sur la recherche des meilleures caractéristiques et de la meilleure façon de représenter le graphique, ainsi que sur le changement d'attention pour s'adapter à ces nouvelles données.
Ci-dessous montre quelques méthodes qui permettent d'obtenir des résultats de pointe ou proches sur l'Open Graph Benchmark de l'Université de Stanford :
Une recherche récente "Les transformateurs purs sont de puissants apprenants de graphes" a introduit TokenGT dans la méthode, représentant le graphe d'entrée comme une série d'intégrations de nœuds et de bords, c'est-à-dire en utilisant des identifiants de nœuds orthogonaux et des identifiants de type pouvant être entraînés. Effectuer une augmentation sans intégrations de position et alimentez cette séquence en entrée de Transformers. Cette approche est très simple et en même temps très efficace.

Adresse papier : https://arxiv.org/pdf/2207.02505.pdf
De plus, dans l'étude de "Recette pour un transformateur graphique général, puissant et évolutif", avec autres méthodes La différence est qu'elle introduit non pas un modèle mais un framework, appelé GraphGPS, qui permet de combiner des réseaux de transmission de messages avec des transformateurs linéaires (à distance) pour créer facilement des réseaux hybrides. Le framework contient également plusieurs outils pour calculer les codages positionnels et structurels (nœud, graphe, niveau de bord), l'augmentation des fonctionnalités, les marches aléatoires, etc.

Adresse papier : https://arxiv.org/abs/2205.12454
L'utilisation de Transformers pour les graphiques en est encore dans une large mesure à ses balbutiements, mais pour l'instant, ses perspectives sont très prometteuses. , cela peut atténuer certaines des limitations des GNN, telles que la mise à l'échelle vers des graphiques plus grands ou plus denses ou l'augmentation de la taille du modèle sans trop de lissage.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Où dois-je indiquer mon lieu de naissance : province, ville ou comté ?
Où dois-je indiquer mon lieu de naissance : province, ville ou comté ?
 Comment résoudre 400 mauvaises requêtes
Comment résoudre 400 mauvaises requêtes
 Quelle est la raison pour laquelle le réseau ne peut pas être connecté ?
Quelle est la raison pour laquelle le réseau ne peut pas être connecté ?
 Utilisation de la fonction get en langage C
Utilisation de la fonction get en langage C
 Comment obtenir une adresse URL
Comment obtenir une adresse URL
 Comment résoudre le problème selon lequel document.cookie ne peut pas être obtenu
Comment résoudre le problème selon lequel document.cookie ne peut pas être obtenu
 Découvrez les dix principales crypto-monnaies dans lesquelles il vaut la peine d'investir
Découvrez les dix principales crypto-monnaies dans lesquelles il vaut la peine d'investir
 utilisation de la paire de sockets
utilisation de la paire de sockets
 qu'est-ce que DriverGenius
qu'est-ce que DriverGenius